
ÍNDICE
Introducción
Clasificación de redes neuronales:
Estructura
Entrenamiento
Aplicación de las redes neuronales a la identificación de sistemas
Las redes neuronales en el control

REDES NEURONALES
Neurona: base del funcionamiento del cerebro.
Sistema de procesamiento cerebral de la información:
Complejo, No lineal y Paralelo.
Elementos de que consta: sinapsis, axón, dentritas y soma o cuerpo

NEURONA ARTIFICIAL
Neurona artificial: unidad de procesamiento de la información, es un dispositivo simple de cálculo que ante un vector de entradas proporciona una única salida.
Elementos:
Conjunto de entradas, xj
Pesos sinápticos, wi
Función de activación: w1·x1+ w2·x2 + … + wn·xn = a
Función de transferencia: y = F (w1·x1+ w2·x2 + … + wn·xn )
Bias o polarización: entrada constate de magnitud 1, y peso b que se introduce en el sumador

NEURONA ARTIFICIAL
Principales funciones de transferencia:
Lineal: y=ka
Escalón: y = 0 si a< 0; y=1 si a>=0
Sigmoide
Gaussiana.

RNA de una capa
Una neurona aislada dispone de poca potencia de cálculo.
Los nodos se conectan mediante la sinapsis
Las neuronas se agrupan formando una estructura llamada capa.
Los pesos pasan a ser matrices W (n x m)
La salida de la red es un vector: Y=(y1, y2, … , yn)T
Y=F(W·X+b)

RNA Multicapa
Redes multicapa: capas en cascada.
Tipos de capas:
Entrada
Salida
Oculta
No hay realimentación => red feedforward
Salida depende de entradas y pesos.
Si hay realimentación => red recurrente
Efecto memoria
Salida depende también de la historia pasada.
Una RNA es un aproximador general de funciones no lineales.

Entrenamiento I
Entrenamiento: proceso de aprendizaje de la red.
Objetivo: tener un comportamiento deseado.
Método:
Uso de un algoritmo para el ajuste de los parámetros libres de la red: los pesos y las bias.
Convergencia: salidas de la red = salidas deseadas.
Tipos de entrenamiento:
Supervisado.
Pares de entrenamiento: entrada – salida deseada.
Error por cada par que se utiliza para ajustar parámetros
No-supervisado.
Solamente conjunto de entradas.
Salidas: la agrupación o clasificación por clases
Reforzado.

Perceptrones
McCulloch y Pitts, en 1943, publicaron el primer estudio sobre RNA.
El elemento central: perceptrón.
Solo permite discriminar entre dos clases linealmente separables: XOR.
0.5= a = w1·x1 + w2·x2
No hay combinación de x1 y x2 que resuelva este problema.
Solución: más capas o funciones de transferencia no lineales.

Aprendizaje del Perceptrón.
Algoritmo supervisado:
Aplicar patrón de entrada y calcular salida de la red
Si salida correcta, volver a 1
Si salida incorrecta
0 ? sumar a cada peso su entrada
1 ? restar a cada peso su entrada
Volver a 1
Proceso iterativo, si el problema es linealmente separable este algoritmo converge en un tiempo finito.
Nos da los pesos y las bias de la red que resuelve el problema.
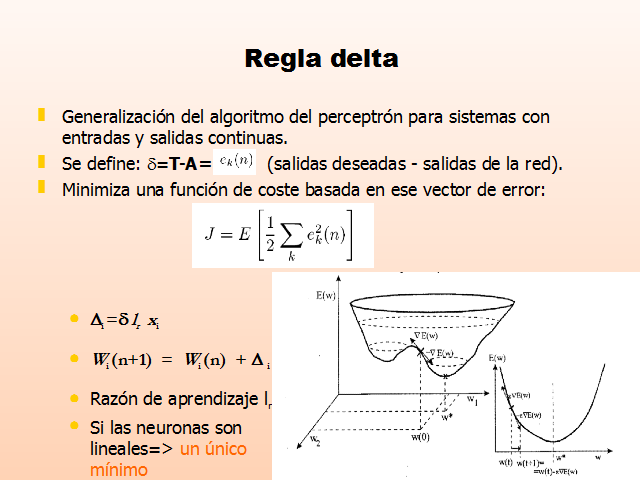
Regla delta
Generalización del algoritmo del perceptrón para sistemas con entradas y salidas continuas.
Se define: d=T-A= (salidas deseadas – salidas de la red).
Minimiza una función de coste basada en ese vector de error:
Di =d lr xi
Wi (n+1) = Wi (n) + D i
Razón de aprendizaje lr
Si las neuronas son lineales=> un único mínimo

Redes Neuronales Lineales.
Función de transferencia lineal.
Algoritmo de entrenamiento de Widrow-Hoff o Delta, tiene en cuenta la magnitud del error.
Entrenamiento:
Suma de los cuadrados de los errores sea mínima.
Superficie de error con mínimo único.
Algoritmo tipo gradiente.
Aproximan funciones lineales.

Backpropagation
Clave en el resurgimiento de las redes neuronales.
Primera descripción del algoritmo fue dada por Werbos en 1974
Generalización del algoritmo de Widrow-Hoff para redes multicapa con funciones de transferencia no-lineales y diferenciables.
1989 Hornik, Stinchcombe y White
Una red neuronal con una capa de sigmoides es capaz de aproximar cualquier función con un número finito de discontinuidades
Propiedad de la generalización.
La función de transferencia es no-lineal, la superficie de error tiene varios mínimos locales.
Página siguiente  |