Problemas básicos de la economía (página 3)

Hagamos un paréntesis por un momento para recordar el procedimiento
utilizado en el estudio de la teoría del comportamiento del consumidor.
Primero se establece la posición de equilibrio del consumidor. Luego
planteamos y contestamos la pregunta siguiente: ¿Cómo cambiara
la combinación de los bienes cuando cambia el precio o el ingreso?
Planteemos ahora el mismo tipo de preguntas desde el punto de vista de un
productor: ¿Cómo cambiaran las proporciones factoriales cuando
cambien el volumen de producción?

Grafica VII.4.2. La combinación optima de los insumos
para maximizar la producción sujeta a un costo dado.

4.5 TEORIA AVANZADA DE PRODUCCION, APLICANDO MODELOS
MATEMATICOS

Los procesos de producción requieren de ordinario una gran diversidad
de insumos. Estos insumos no son tan simples como "trabajo", "capital"
y "materias primas"; normalmente se utilizan muchos tipos cualitativamente
diferentes de cada insumo para producir un bien.

Suponemos que solo hay un insumo variable, donde lo llamaremos "trabajo",
aunque cualquier otro insumo podría desempeñar la misma función.
Suponemos que este insumo variable pude combinarse en proporciones diferentes
con un insumo fijo para producir diversas cantidades del bien en cuestión.
Llamamos "tierra" al insumo fijo; en la discusión emplearemos
un ejemplo específico de la producción: la producción
agrícola.

Insumos fijos y variable, el corto y el largo plazo

Al analizar el procedo de la producción física y de los
costos de producción estrechamente relacionados, convendrá introducir
una distinción arbitraria: la clasificación de los insumos en
fijos y variable. En concordancia definimos un insumo fijo como aquel cuya
cantidad no pueda cambiarse fácilmente, cuando las condiciones del
mercado indican que es deseable un cambio inmediato en la producción.
En realidad, ningún insumo esta jamás absolutamente fijo, por
corto que sea el periodo considerado. Pero en aras de la sencillez analítica
manteniendo fijos algunos insumos, razonando que estos insumos son en efecto
variables, pero el costo de la variación inmediata es tan grande que
se descarta tal acción para la decisión particular en cuestión.
Los edificios, las grandes maquinas, el personal directivo, son ejemplos de
insumos que no pueden aumentarse o reducirse con rapidez. En cambio, un insumo
variable es aquel cuya cantidad podría cambarse casi instantáneamente
en respuesta a los cambios deseados en la producción. Muchos tipos
de servicios de trabajo y los insumos de materias primas y procesadas caen
en esta categoría.

En relación con la distinción de los insumos fijos y
variables, los economistas introducen otra distinción: el corto y el
largo plazo. El corto plazo se refiere al periodo en el que esta fijo el insumo
de uno o más agentes productivos. Por lo tanto, los cambios en la producción
deben realizarse solo mediante ciertos cambios en el uso de los insumos variables.
Por ejemplo, si un productor desea aumentar la producción en el corto
plazo significa de ordinario el uso de mas horas de servicio de la mano de
obra con la planta y el equipo existente. De igual modo, si el productor desea
reducir la producción en el corto plazo, podrá deshacerse de
ciertos trabajadores; pero no se puede "deshacer" de inmediato un
edificio o una locomotora diesel, aunque su uso puede bajar a cero.

En el largo plazo, sin embargo, aun esto es posible, pues el largo
plazo se define como el periodo (u horizonte de plantación) en el que
todos los insumos son variables. En otras palabras, el largo plazo se refiere
al momento futuro en el que los cambios en la producción pueden realizarse
en la forma más ventajosa para el empresario. Por ejemplo, en el corto
plazo un productor podrá incrementar la producción solo mediante
la operación de la planta existente durante más horas diarias.
Por supuesto, esto implica el pago de horas extras a los trabajadores. En
el largo plazo puede resultar más económica la instalación
de una planta adicional para volver al horario de trabajo normal.

En este capitulo nos interesa fundamentalmente la teoría de
la producción en el corto "plazo, combinando diferentes cantidades
de insumos variables con una cantidad especifica de insumo fijo para producir
diversas cantidades del bien en cuestión. La organización de
la producción en el largo plazo se determina en gran medida por el
costo relativo de la producción de una cantidad deseada mediante diferentes
combinaciones de insumos.

Proporciones fijas y variables

Como indicamos antes, la discusión final se centra en gran medida
en el uso de una cantidad fija de un insumo y de una cantidad variable de
otro insumo para producir cantidades variables de un bien. Esto significa
que nuestra atención se limita principalmente a la producción
en condiciones de producciones variables. La razón de las cantidades
de insumos puede variar; por lo tanto, el empresario debe determinar no solo
el nivel de la producción, sino también la producción
optima en que se combinaran los insumos (en el largo plazo).

El principio de las producciones variables puede enunciarse de dos
formas distintas. Primero, la producción con proporciones variables
implica que la producción podrá cambiarse en el corto plazo,
cambando la cantidad de los insumos variables utilizada en cooperación
con los insumos fijos. Naturalmente, a medida que cambia la cantidad de insumos,
mientras el otro permanece constante, cambia la razón de los insumos.
Segundo, cuando la producción esta sujeta a proporciones variable,
puede producirse la misma cantidad con diversas combinaciones de insumos,
es decir, con diferentes razones de insumos. Esto podría aplicarse
solo al largo plazo, pero es pertinente para el corto plazo cuando hay más
de un insumo variable. Por ejemplo, el trigo puede producirse con mucho trabajo
y muy poca maquinaria, o puede producirse con muy poco trabajo y un tractor,
el que puede rentarse por semana.

La mayoría de los economistas consideran la producción
en condiciones de proporciones variables como típica tanto del corto
como del largo plazo. No hay duda, desde luego, de que las proporciones son
variables en el largo plazo. Al tomar una decisión de inversión,
un empresario podría escoger entre una gran diversidad de procesos
de producción diferente. Por ejemplo, un automóvil puede hacerse
casi a mano o con las técnicas del ensamblado en línea. En el
corto plazo, sin embargo, puede haber algunos casos en los que la producción
este sujeta a proporciones fijas.

La producción con proporciones fijas significa que solo hay
una razón de insumo que puede usarse para producir un bien. Si la producción
se expande o se contraer, todos los insumos deben expandirse o contraerse
para mantener fija la razón de insumo. Esta es la tecnología
común en la elaboración de un pastel. Si la receta indica media
taza de leche y tres tazas de harina, no podremos producir el mismo pastel
usando por ejemplo dos tazas de leche dos tazas de harina. Pero si podemos
producir dos pasteles con una taza de de leche y seis de harina. Los factores
se usan en proporciones fijas.

4.6 COSTOS

Las condiciones físicas de la producción, el precio de
los recursos y las eficiencias económicas de un empresario determinan
conjuntamente el costo de producción de una empresa. Le función
de producción proporciona la información necesaria para trazas
el mapa de isocuantas. Los precios de los recursos determinan las curvas de
isocostos. Por ultimo, la eficiencia del empresario dicta la producción
de cualquier volumen mediante la combinación de insumos que igualan
la tasa marginal de sustitución técnica con la razón
de precios de los insumos. Por lo tanto, cada punto de tangencia determina
un nivel de producción y su costo total asociado. A partir de esta
información, podemos construir un cuadro, una curva, o una función
matemática que relacione el costo total con el nivel de producción.
Este es el esquema de costo, o función de costo, que constituye unote
los temas de este capitulo.

Sin embargo, este no es el único tema que abordaremos, ya que
en el corto plazo, por definición, no todos los insumos son variables.
Algunos son fijos, y el empresario no puede alcanzar instantáneamente
la combinación de insumos que corresponde a la eficiencia económica
(es decir, la que iguala la tasa marginal de sustitución técnica
con la razón de precios de los insumos). En el corto plazo por lo general
no se obtiene un punto de la ruta de expansión. En consecuencia, no
solo debemos analizar el costo en el largo plazo sino también en el
corto plazo.

Para muchos propósitos, es necesario considerar las relaciones
de las isocuantas y los isocostos. En general, para entender el componente
de las empresas basta con entender las curvas de costo y como se desplazan
cuando cambian los precios de los insumos y la tecnología. Sin embargo,
existe una representación de isocuantas e isocostos de cualquier problema
que puede discutirse con curvas de costos.

No obstante, antes de revisar la mecánica del análisis
de los costos, conviene considerar por un momento una perspectiva más
amplia y plantearnos esta pregunta "¿Cuáles son exactamente
los costos legítimos de la producción?" Esta pregunta tiene
dos respuestas que, en circunstancias ideales, resultan idénticas.

Los economistas se interesan en el costo social de la producción,
o sea el costo en que incurre una sociedad cuando se utilizan sus recursos
para producir un bien determinado. En todo momento una sociedad posee una
concentración de recursos, de propiedad individual o colectiva, según
la organización política de la sociedad en cuestión.
Desde un punto de vista social, el objetivo de la actividad económica
es obtener la mayor producción posible con este conjunto de recursos.
Por supuesto, lo "posible" no depende solo de la utilización
eficiente y plena de los recursos, sino también de la lista especifica
de los bienes que se produzcan. Es obvio que una sociedad podría alcanzar
una producción mayor de automóviles si solo se produjeren automóviles
compactos pequeños. Los automóviles más grande y mas
lujosos requieren mas de casi todos los insumos. No obstante, en sus esquemas
privados de evaluación, algunos miembros de la sociedad podrían
asignar mayor importancia a los automóviles lujosos que a los compactos.

El equilibrio del costo relativo de los recursos utilizados en la producción
de un bien con su conveniencia social relativa requiere el conocimiento de
las evaluaciones sociales y del costo social.

El costo total del uso de un conjunto de recursos para producir una
unidad del bien X es el numero de unidades del bien Y que deben sacrificarse
en el proceso. Se utilizan recursos para producir tanto X como Y (y todos
los demás bienes). Los recursos utilizados en la producción
de X no pueden usarse en la producción de Y ni en la de ninguno otro
bien. Para ilustrar esto con un ejemplo sencillo, ponemos en Robinson Crusoe,
que vivía solo en una isla y se mantenía con la pesca y la recolección
de cocos. El costo para Crusoe de un pescado adicional se mide por el número
de cocos que debe sacrificar por tener que pasar más tiempo pescado.

Este concepto del costo, o como se le llama mas frecuentemente, el
costo de producción alternativa o de oportunidad, capta mucho de la
esencia de la economía. Desafortunadamente, este concepto del costo
a menudo se pasa por alto en las discusiones populares de cuestiones de política
pública y privada. Por ejemplo, algunos portavoces del Congreso se
oponen a menudo a la política de un ejército formado solo voluntarios,
alegando que "cuesta" demasiado en relación con un ejército
de reclutamiento. El error de este razonamiento estriba en que la paga del
gobierno a los individuos que son reclutados para el ejercito militar no constituye
la medida adecuada del costo social del reclutamiento. Los individuos que
son reclutados para el servicio militar son sacados a menudo de empleos civiles
en los que están produciendo bienes y servicios tales como vivienda
y automóviles, o servicios médicos y educativos. Al reclutar
a esos individuos para las fuerzas armadas, la sociedad debe sacrificar algunos
de estos bienes y servicios, y esta producción sacrificada es la medida
apropiada del costo del reclutamiento.

• Costo de oportunidad.- El costo alternativo o de oportunidad
  de la producción de una unidad de bien X es la cantidad del bien
  Y que debe sacrificar para utilizar recursos en la producción de
  X en lugar de Y. este es el costo social de la producción de X.

• Costo de producción.- Es el gasto que se utiliza
  para producir una mercancía y que se encuentra determinado por
  el pago de sueldos y salarios, el costo de todos los insumos realizados,
  la depreciación para reponer el desgaste del capital fijo y la
  ganancia media del capital empleado para su producción.

• Costo económico.- También llamados empresariales,
  son los gastos que realiza la empresa para llevar acabo sus funciones
  como unidades de producción, entre ellos sobresalen: maquinaria,
  equipo, materias primas, fuerza de equipo y en general gastos de producción.

• Costo estimado.- Es el costo que se le da a una cosa, a
  una operación, a una transacción, antes de que se produzca.
  El costo estimado se basa en el conjunto de gastos en el que se incurre
  para producir algo.

• Costo fijo.- Es el gasto que se realiza para producir mercancías
  y que no cambia aunque varié el volumen de producción o
  se produzca otra mercancía. Los costos fijos de una empresa representan
  el pago de todos los factores fijos empleados en la producción.
  Los costos fijos no cambian en el corto plazo, aunque a largo plazo todos
  los costos se pueden modificar ejemplo de costos fijos son: contrato de
  arrendamiento ya firmado, sueldo y salario ya negociable en un contrato
  colectivo, publicidad pagada por anticipado, etc.

• Costo marginal.- Es el desembolso que realiza un oferente
  cuando produce una unidad mas del producto; es decir, es un gasto adicional
  que ocurre cuando se produce una unidad mas de producto; es decir, es
  un gasto adicional que ocurre cuando se produce una unidad mas. El costo
  marginal se puede obtener dividiendo el incremento del costo variable
  total (ya que el costo total solo varia a causa de cambios en costo variable
  total) entre el producto marginal. Matemáticamente el costo marginal
  se define como la tasa de cambio o primera derivada de la función
  del costo total.

• Costo medio.- Es el gasto de producción promedio,
  que se obtenga dividiendo el costo total entre el número de unidades
  producidas. El costo medio o promedio también se puede obtener
  sumando el costo fijo medio y el costo variable medio.

• Costo total.- Es la suma de todos los gastos que se realizan
  para la producción; representa la suma de los costos fijos totales
  y los costos variables totales.

• Costo variable.- Es el gasto que se realiza en la producción
  cambia cuando varían los volúmenes de producción.
  El costo variable representa el pago de los factores variables de la empresa.
  El administrador de la empresa debe tener el control de estos costos durante
  el proceso de producción, para que no se eleven innecesariamente.
  Los costos variables son: material primas, trabajo, servicios públicos,
  suministro de materiales, etc.

• Costo.- Es el gasto que se hace para producir una mercancía;
  esta determinada por la cantidad de trabajo incorporado en la misma, lo
  que representa una definición objetiva, por su parte, los subjetivistas
  afirman que el costo son las oportunidades de producir a los que se renuncia,
  es decir, el costo de una mercancía se mide por lo que se pierde
  al no producir otra mercancía.

• Costos implícitos.- Los costos implícitos
  en que incurre un empresario para producir un bien especifico consiste
  en las sumas que hubiera podido ganar con el mejor uso alternativo de
  su tiempo y dinero. Un empresario obtiene un beneficio económico
  neto en la producción de X si, u solo si, sus ingresos totales
  exceden la suma de sus costos explícitos e implícitos.

4.4.1 COSTO A CORTO PLAZO

Los procesos productivos utilizan recursos los mismos que son procesados
con la finalidad de obtener un producto.

A continuación, se desarrollará un modelo microeconómico
que explica la relación del uso de recursos y el producto obtenido
en un escenario de corto plazo.

Un proceso productivo es de corto plazo cuando por lo menos uno de
los factores de producción no variaría durante todo el proceso
productivo.

Normalmente el factor fijo es el capital y la infraestructura. El capital
puede ser las máquinas, plantas de producción, las mismas que
fácilmente no varían a menos que el empresario invierta y expanda
su capacidad instalada.

Definamos la función de producción de corto plazo de
la siguiente manera:

Q = f ( K , L )

donde "Q" es la tasa de producción, medida en cantidades
de bienes , "K" es el capital, medida en horas de uso de las máquinas
(o cantidad de máquinas) y "L" es el recurso humano o comúnmente
denominado la mano de obra, medido en horas hombre (o cantidades de personas);
estos dos últimos factores deben coincidir en el tiempo empleado; por
ejemplo, se puede medir el capital por horas de uso semanal, pueden existir
dos o tres máquinas, y la planta puede contar con 50 horas hombre a
la semana, distribuidos durante los días de la semana. La hora hombre
significa que un hombre ha trabajado una hora, y 10 horas hombre significan
que un hombre ha trabajado 10 horas pero también puede significar que
dos hombre han trabajado 5 horas, digamos, en un día de labor. En tal
sentido, para efectos de costos, lo que importa es que habrá que pagar
10 horas de salario.

La función de producción de corto plazo cuenta así
con factor fijo, el capital (K). Esta función tiene una característica
muy importante que consiste en que a medida que aumenta el uso del factor
variable en el proceso productivo, el capital se mantiene constante, la producción
aumentará pero no de manera lineal sino de manera decreciente.

Si observamos la figura Nº 1 en el eje vertical se tiene el producto
y en el eje horizontal se mide el recurso variable, la mano de obra.

Ideal sería que el producto aumente de manera lineal ante aumentos
del uso del recurso variable, pero el producto aumenta inicialmente en proporciones
cada vez mayores y a partir de cierta cantidad del uso del recurso variable,
el producto, si bien es cierto sigue aumentando, lo hace pero cada vez en
proporciones menores.

Esta explicación se resume en la curva de la figura Nº
1, donde se puede observar que el producto se incrementa de manera no lineal.
Inicialmente la curva aumenta de manera creciente, del punto 0 al punto "a",
es decir las tangentes de la curva poseen una mayor pendiente a medida que
aumenta el uso de la mano de obra y por

Consiguiente, el producto. A partir del punto "a", el producto
sigue aumentando pero cada vez en menores proporciones. Esta curva se torna
cóncava hacia abajo a diferencia del caso anterior que era de concavidad
hacia arriba. Se puede así desprender de este análisis gráfico
que el punto "a" es un punto de inflexión, en sentido matemático,
pero en términos económicos, a partir de dicho punto se presenta
lo que los economistas llaman "la ley de los rendimientos marginales
decrecientes (LRMD)".

Esta ley consiste en los siguientes:

" un proceso productivo que se caracteriza por contar por
lo menos con un recurso o factor fijo y uno o más recursos variables,
a medida que aumenta el uso de estos últimos, el producto aumenta inicialmente
de manera creciente, pero a partir de cierta utilización de los recursos
variables, si bien es cierto el producto sigue aumentando, pero lo hará
de manera decreciente hasta llegar a un valor máximo, y de allí,
si se sigue incrementando el uso del recurso variable, el producto empieza
inclusive a disminuir".

La pregunta que se podría plantear es, ¿qué significa
crecer de manera decreciente?. La respuesta la vemos en la curva de la figura
Nº 1. Cuando se utiliza la mano de obra de "0" hasta "a",
la curva es cóncava hacia arriba, lo que significa que las rectas tangentes
a la curva cada vez tendrán un mayor ángulo. A partir del punto
"a", las rectas tangentes a la curva tendrán menor pendiente,
hasta llegar al punto "c" donde la recta tangente tiene una pendiente
de cero, ya que es horizontal; y a partir del punto "c", la pendiente
de la recta tangente a la curva es negativa.

En sentido económico, la pendiente de la curva tangente es la
variación del producto ante un aumento del uso de la mano de obra en
el proceso productivo. Si utilizamos valores discretos, es decir, enteros,
de uno en uno, esta pendiente nos da la información de cuanto aumenta
el producto cuando aumenta en una unidad el uso de la mano de obra, pero esta
"tangente" sería realmente una secante ya que "corta
a la curva" en dos puntos, dependiendo del distanciamiento de éstos.

Si el cambo del uso de la mano de obra es infinitamente pequeño,
la pendiente se puede medir a través de la derivada de la función
de producción. La ventaja de esta técnica es que facilita enormemente
el análisis cualitativo. En este caso se utiliza el cálculo
diferencial a través de las técnicas de la primera y segunda
derivada.

El producto marginal es la razón de cambio del producto versus
mano de obra, dada una intensidad del factor fijo, en este caso el capital.
Si observamos la figura Nº 1, las pendientes de la curva es el producto
marginal, el mismo que aumenta inicialmente hasta el punto "a",
llegando a un máximo valor hasta el punto "c" en que tiene
un valor de cero, y de allí se torna negativo.

Si aplicamos la derivada al producto marginal tendríamos la
segunda derivada de la función de producción. En término
matemático, la segunda derivada nos da el punto de inflexión,
que es el punto "a", es decir, se da un cambio en la concavidad
de la curva. También el punto de inflexión nos da el valor máximo
del producto marginal. Al derivar el producto marginal e igualar a cero, se
obtiene el máximo del producto marginal y el punto de inflexión
de la curva original del producto.

Respecto al producto medio, se tiene la siguiente fórmula:

Si analizamos la curva de la figura Nº1, el producto medio es
la tangente del ángulo que forma la línea que parte del vértice
(la que llamaremos rayo que parte del origen) y corta la curva en cada uno
de los puntos. Por ejemplo, en el punto "a", tenemos un rayo que
pasa por este punto y forma un ángulo determinado; la tangente de este
ángulo es el producto medio, porque la tangente al ser el cateto opuesto
entre el cateto adyacente, lo que se está dividiendo realmente, es
el producto (distancia vertical) entre cantidad de mano de obra (distancia
horizontal desde el origen).

También en el punto "a" tenemos una tangente, que
es el producto marginal, luego, en este punto se puede medir un producto medio
y un producto marginal. Vemos así que en el punto "a" el
producto marginal es mayor que el producto medio porque la recta tangente
tiene un mayor ángulo que el que forma el rayo que parte del origen,
que dicho sea de paso, pasa por el punto mencionado.

Si analizamos el punto "b", en este punto coincide el ángulo
que forma la recta tangente y el rayo que parte del origen. Esto significa
que el producto medio será igual que el producto medio. Y en el punto
"c", la tangente tiene un ángulo cero lo que no sucede con
el ángulo del rayo que parte del origen, lo que significa que el producto
medio es mayor que el producto marginal.

Resumiendo, inicialmente el producto marginal es mayor que el producto
medio, luego se hacen iguales y de allí, el producto medio es mayor
que le producto marginal. Si analizamos figura Nº2, tenemos un doble
gráfico donde se relaciona la curva original del producto con el producto
marginal y el producto medio. Desde el punto de origen hasta "La",
el producto marginal aumenta y luego empieza a disminuir hasta "Lc",
donde se torna negativo. El producto medio aumenta hasta "Lb" y
de allí comienza a disminuir.

Vemos así que mientras el producto medio está aumentando,
el producto marginal es mayor que el producto medio, y cuando el producto
medio disminuye, significa que el producto marginal es menor que el producto
medio. O visto desde otro ángulo, cuando el producto marginal es mayor
que el producto medio, éste aumenta, y cuando el producto marginal
es menor que el producto medio, éste disminuye.

Una conclusión que se puede dar es que la curva del producto
medio corta en dos a la curva del producto medio por el valor más alto
de este último. Esta relación entre estas dos curva se presenta
dada la doble concavidad de la curva original del producto. Y la doble concavidad
de la curva original existe porque se asume la LRMD, explicada anteriormente.
Esta ley, que en el sentido estricto de la palabra no es una ley, es realmente
un supuesto empírico, o un axioma de la teoría ya que se asume
como una verdad inicial sin demostración científica.

Hay ciertos insumos cuyo uso no se puede cambiar, cualquiera que sea
el nivel de la producción. Asimismo, hay otros insumos, llamados insumos
variables, cuyo uso si se puede cambiar. El corto plazo es un concepto más
nebuloso. En un nanosegundo no se puede cambiar virtualmente nada en el proceso
de producción. En un día, quizá se puede intensificar
el uso de ciertas maquinarias; en un mes, el empresario podría rentar
algún equipo adicional; en un año, quizá podría
construirse una nueva planta.

El análisis del costo total en el corto plazo depende de dos
proposiciones: a) las condiciones físicas de la producción y
los precios unitarios de los insumos determinan el costo de producción
asociado a cada nivel de producción posible; y b) el costo total pueden
dividirse en dos componentes: el costo fijo y el costo variable.

Supongamos que un empresario tiene una planta fija que puede utilizarse
para producir cierto bien. Supongamos además que esta planta cuesta
$100 el costo fijo es por lo tanto $100, es decir, es constante cualquiera
que sea el nivel de producción. Esto se muestra en el cuadro VIII.3.1
mediante la columna de datos de $100 llamadas "costo fijo total".
También esta indicación por la línea horizontal llamada
CFT en la grafica VIII.3.1. El cuadro y la grafica destacan que el costo fijo
esta, en efecto, fijo.

Si la producción es mayor que cero, también deben usarse
insumos variables. No importa cual se elija, ya que un aumento en el nivel
de producción requiere un aumento en el uso de los insumos, ya sea
que se trate de un insumo variable o de muchos insumos variables utilizados
en una combinación optima. En cualquier caso, cuanto mayor sea el nivel
del insumo variable mayor será el costo variable total. Esto se muestra
en la columna 3 del cuadro VIII.3.1 y en la curva CVT en la grafica VIII.
3.1.

Sumando el costo fijo total y el costo variable total se obtiene el
costo total, que se encuentra representado por las entradas de la última
columna del cuadro VIII.3.1 y por la curva CT de la grafica VIII.3.1. Podemos
ver en la grafica CT y CVT se mueven juntas y son, en cierto sentido, parábolas.
Esto quiere decir que las pendientes de ambas curvas son iguales en cada punto
de la producción; y en cada punto, ambas curvas están separadas
por una distinción vertical de $100 que es el costo fijo total. Las
curvas parecen irse aproximando una a la otra, pero esto ocurre porque el
ojo se enfoca en la distancia mas corta entre las curvas, no en la distancia
vertical. En efecto, la distancia vertical permanece constante, porque el
costo que separa a las curvas, es decir, el costo fijo total, no cambia con
el nivel de producción.

Hemos observado que en realidad hay un gran número de "cortos"
plazos, dependiendo del periodo involucrado. Cada corto plazo se caracteriza
por el hecho de que no todos los factores de producción pueden ajustarse
plenamente en el periodo dado. Para apreciar la importancia de esta consideración,
supongamos que una empresa desea incrementar su producción y tiene
que adquirir otras 150 maquinas fresadoras para hacerlo al menos costo posible
(es decir, el optimo en el largo plazo requiere otras 150 fresadoras). En
concreto, supongamos que hay cuatro "cortos" plazos, cada uno de
ellos tres meses más largos que el anterior. A causa de demoras en
la entrega, no se pueden instalar fresadoras nuevas en los primeros tres meses,
pero el calendario de entrega permite instalar 50 fresadoras adicionales en
cada uno de los trimestres siguientes. Por consiguiente, el ajuste en el largo
plazo (un año en este caso) implica una adicción de 150 fresadoras,
la cual se realiza en tres etapas. En el plazo mas costo (3 meses) no se dispone
de fresadoras nuevas, en el plaza de 6 meses hay 50 fresadoras nuevas, en
el plazo de 9 meses hay 100 fresadoras nuevas, y en el largo plazo (12 meses)
hay 150 fresadoras nuevas. A fin de producir en el nuevo nivel, se necesitan
cantidades de trabajo diferentes en cada periodo trimestral. Suponemos que
las horas-hombre pueden ajustarse libremente en cualquier momento, utilizando
el empleo de horas extras y tiempo parcial. (Para simplificar la exposición,
suponemos también que la tasa salarial no aumenta por las horas extras).
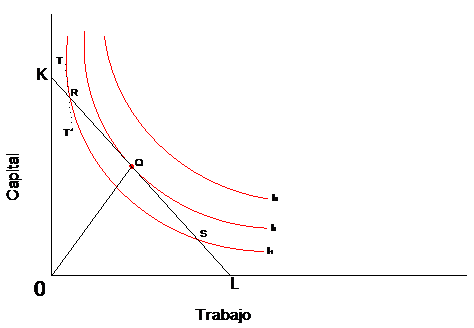
Esta situación se muestra en la grafica VIII.2.2.

En esta grafica, la producción inicial esta dada por la isocuanta
Q0´ y por la nueva producción, más alta, se indica por la isocuanta
Q1. Durante el primer trimestre (el plazo mas costo), se produce Q1 con el
acervo de fresadoras existente (K1= K0= 30) y con L1 horas-hombre. El costo
total para el empresario en este periodo esta dado por la línea de
isocosto C1. Adviértase que la línea de isocostos no es tangente
a Q1 en el punto A. esto es así, porque la empresa no puede obtener
fresadoras adicionales en los primeros tres meses. Dado el acervo existente
de 30 fresadoras, el procedimiento mas barato para la obtención de
producción Q1 es un incremento sustancial de las horas-hombre (de L0
a L1).

Durante los tres meses siguientes se reciben 50 fresadoras nuevas,
de manera que el acervo9 total de las fresadoras aumenta a K2 (K2= 80= K1
+ 50). Esto permite que los empresarios reduzcan el empleo de horas extras
y de tiempo parcial a L2. también de reduce el costo de la producción
de Q1, porque, como puede apreciarse fácilmente en la grafica VIII.2.2,
la línea de isocosto C2 se encuentra al suroeste de la línea
de isocosto C1. En virtud de que el acervo de capital es menos que el óptimo
de 180 fresadoras en el largo plazo, sigue siendo cierto que línea
de isocosto C2 no es tangente a Q1. Durante los 3 meses siguientes se reciben
otras 50 fresadoras y la línea de isocostos de desplaza a C3.

Finalmente de alcanza el equilibrio en un año, cuando se dispone
de 180 fresadoras. En este nivel, la línea de isocostos C4 es tangente
a Q1, y Q1 se esta produciendo al menor costo posible, dados los precios de
los factores y la función de producción.

Existe un diagrama en el espacio costo-volumen de producción
que corresponde a la figura A de la grafica VIII.2.2. Esto se muestra en la
figura B. el punto A´ corresponde al punto A del a figura A. Allí el
costo es C1 y el volumen de producción es Q1. El punto B´ corresponde
al punto B de la figura A. Allí la producción es Q1 de nuevo,
pero el costo es solo C4. Por lo tanto, CTLP nos da la relación del
costo total cuando todos los factores son variables. CTCP1 nos da la relación
de costos cuando solo el trabajo es variable. Las otras curvas. CTCP2 y CTCP3,
son los casos intermedios que muestran lo que seria el costo total, si el
capital pudiera incrementarse en alguna medida pero no todo lo deseable. Adviértase
que todas las curvas coinciden en el punto D. la causa es que la solución
en el costo plazo y la solución en el largo plazo son iguales en ese
punto, por que aun en el caso de que la empresa pudiera modificar su capital,
seleccionaría el nivel actual de 30 unidades de capital para producir
el nivel Q0.

Este ejemplo ilustra el punto esencial de que cuando menos sea el plazo,
mas costosa resultara la producción de volúmenes distintos de
aquel para el cual el acervo de capital corriente (es decir, el volumen dado
por Q0 es este ejemplo) sea óptimo. Los costos en el largo plazo para
la producción de un volumen dado nunca serán mayores que los
costos de producción de ese volumen en el corto plazo.

La teoría dinámica de los costos en el corto y en el
largo plazo puede elaborarse de diversa maneras. Por ejemplo, se pueden introducir
explícitamente los costos del ajuste para obtener modelos de acumulación
óptima de capital. Sin embargo, a fin de concentrarnos en los resultados
importantes de estática comparativa, nos apegaremos a la dicotomía
tradicional entre el corto y el largo plazo. En otras palabras, aunque reconocemos
que hay muchos cortos plazos, concentraremos nuestra atención en un
periodo de corto plazo dado por conveniencia de la exposición.

4.4.2 COSTO A LARGO PLAZO

El largo plazo se relaciona con el mundo del planeamiento porque es
más que toda una visualización de cómo evolucionaría
la producción cuando el capital y la mano de obra varían y expanden
la capacidad productiva de una empresa.

En tal sentido, el lago plazo es una visualización de la estructura
productiva de una empresa o unidad de negocios. En este caso, se hace necesario
plantear los costos para diferentes capacidades instaladas, vale decir, para
diferentes combinaciones de capital y mano de obra.

Si asumimos que el costo de oportunidad del capital es "r"
por unidad de tiempo, y que el costo de la mano de obra es "w" por
unidad de tiempo, y que la cantidad de capital se representa por "K",
y que la cantidad de mano de obra será "L", entonces el costo
para un nivel de producción determinado por la combinación de
capital y mano de obra será:

Donde "w.L" son los costos del recurso humano en un periodo
de tiempo, y "r.K", son los costos de oportunidad del capital. Así,
los costos económicos de la producción en nuestro modelo será
la suma de los costos del uso del capital (costos de oportunidad) y los costos
de la mano de obra. En el primer caso, no son los costos de mantenimiento
ni los costos de adquisición del capital, como en muchas oportunidades
se dice. Los costos del capital se pueden comparar a un alquiler de las máquinas
que conforman el acervo de capital de la empresa, aún si el propietario
de las máquinas sea el empresario. Sería un error no considerar
estos costos porque estas máquinas pueden ser utilizadas en una segunda
alternativa y generar una renta. Entonces el hecho de usar las máquinas,
generan una pérdida de ingresos alternos que son denominados el costo
de oportunidad del capital. Lo más simple para el entendimiento de
un costo de oportunidad del capital es asumir que las máquinas que
conforman el capital de la empresa han sido alquiladas.

En el caso del recurso humano, el costo se da por unidad de tiempo,
pudiendo ser por hora, semana o mes. Se asume que este costo es realmente
el precio del servicio de la mano de obra. Existe una demanda por parte de
las empresas del recurso humano y una oferta que son las personas que ofrecen
sus servicios para un periodo determinado. En tal sentido, el costo del recurso
humano es el retorno monetario del servicio ofrecido por las personas en el
mercado de trabajo. El modelo que usaremos asume que el costo del recurso
humano se fija en el mercado por la interacción de la oferta y demanda.

4.7 EL EQUILIBRIO DEL PRODUCTOR

El equilibrio del productor se alcanza cuando maximiza su producción
para un desembolso total determinado; es decir, cuando alcanza la isocuanta
más alta, lo cual ocurre cuando ésta es tangente al isocosto.
Lo anterior es análogo al equilibrio del consumidor, cuando la curva
de indiferencia más alta es tangente a la línea de restricción
presupuestal.

Matemáticamente, se dice que el productor alcanza el equilibrio
cuando:

Lo anterior significa que en el equilibrio el producto marginal del
último peso (peseta, dólar, etc.) invertido en trabajo es igual
al producto marginal del último peso invertido en capital. Lo mismo
sería cierto para otros factores, si la empresa tuviera más
de dos factores de producción.

Ruta de expancion

La ruta de expansión de la empresa se obtiene al unir los puntos
de equilibrio de las diferentes isocuantas e isocostos obtenidos al variar
el desembolso total, por lo cual es análoga a la curva ingreso-consumo.

La Función de Producción

El objetivo de la función de producción es visualizar
como evolucionaría la producción con diferentes combinaciones
de capital y mano de obra. En adición, la función de producción
de largo plazo hace las veces de instrumento para visualizar la evolución
de los costos de largo plazo. En resumen, la función de producción
de largo plazo es la estructura del uso de los recursos y nos da la información
para visualizar los costos del uso de los recursos así como los costos
totales de la producción, para diferentes capacidades instaladas de
una empresa

Asumimos una función de producción de coeficientes fijos
o combinaciones fijas de capital y mano de obra. La combinación de
capital y mano de obra da como resultado un nivel de producción. La
característica más resaltante de esta función de producción
es que las cantidades de capital y mano de obra que se utilizan se mantienen
constante aún si la producción aumenta. Por ejemplo, supongamos
que para producir una mesa en una hora se requiere de un carpintero, y también
se necesita el uso de las herramientas por una hora. Esta es una función
de producción que nos da la información que la relación
entre el recurso humano y el capital es de uno a uno, en un periodo de tiempo.
Pero si necesitamos producir dos sillas en una hora, entonces requeriremos
2 carpinteros y dos unidades de capital. Este capital puede ser un conjunto
de herramientas como el cepillo, el serrucho, etc.

Si el tiempo no es resaltante para la producción, entonces este
mismo carpintero puede producir dos sillas pero en dos horas. Entonces será
importante para la empresa el tiempo en que se desea obtener las dos sillas.

En nuestro modelo se asumirá que la función de producción
está definida para un periodo de tiempo, pudiendo ser una hora, una
semana o un mes, inclusive un año. Es importante tener claro este concepto
relacionado al tiempo porque, como vimos en el ejemplo anterior, el objetivo
de producir las dos sillas puede lograrse en diferentes periodos.

Otro aspecto muy importante, en adición a definir el periodo
de tiempo, es la tecnología y la habilidad empresarial para la producción.
Si regresamos a nuestro sencillísimo ejemplo, asumimos que el carpintero
puede producir una mesa en una hora, pero realmente influyen muchos factores
como: el ambiente de trabajo, el ánimo, la calidad del instrumental,
la habilidad del carpintero, el aprendizaje y la experiencia de esta persona,
y la forma de trabajar. En síntesis, la tecnología se puede
relacionar con las herramientas que utilizan el carpintero y también
como las utiliza; y el aspecto humano, que se relaciona con la determinación
y motivación para hacer el trabajo. Ambos influyen en la productividad
del recurso humano, que para nuestro ejemplo es cuantas mesas produce en una
hora. Entonces, si en una hora produce una mesa, y usa una unidad de capital,
tendríamos que el coeficiente tecnológico del recurso humano,
que definimos con la letra "a" será:

Este coeficiente nos da la información de cuantos recursos humanos
o unidades de mano de obra, o en otro lenguaje, cuantas personas se necesitan
para producir una determinada cantidad de mesas. El coeficiente es de uno,
pero sus unidades son de mesas entre hombre.

El caso del capital, es similar, porque para producir una mesa en una
hora, se necesita una unidad de capital y no más.

Si multiplicamos cada uno de los coeficientes tecnológicos por
la cantidad de recursos disponibles para la producción, obtendríamos
una cantidad de producto en una unidad de tiempo.

En el caso que se disponga, por ejemplo, de cinco carpinteros y solamente
dos unidades de capital, el capital será los recursos limitante y el
recurso humano será el recurso abundante. En sentido inverso, si se
cuenta con cinco unidades de capital y solamente dos unidades de mano de obra,
entonces la mano de obra sería el recursos limitante, en cambio, el
capital sería el recuso abundante. Vemos así que uno de los
recursos definirá cuanto se puede producir y este recurso sería
el limitante en la producción.

La función de producción sería entonces formalizada
de la siguiente manera:

Las letras MIN significa que la producción es definida por el
valor mínimo de "aL" y de "bk". Ambas expresiones
nos reflejan la cantidad de producto que se obtiene con una cantidad de recursos,
dado los coeficientes tecnológicos. El caso óptimo es cuando:

Supongamos que el primer miembro es mayor que el segundo, entonces
la mano de obra es abundante y el capital es el factor que limita y "define"
el nivel de producción.

Si le damos otra forma a la anterior ecuación:

Esta ecuación nos dice que la intensidad del capital respecto
a la mano de obra es igual al ratio de productividades.

Si analizamos el ratio de las productividades tenemos:

Si efectuamos la división, quedan las siguientes unidades

Este ratio nos da la información de la cantidad de unidades
de capital entre la cantidad de unidades de recurso humano. En otras palabras,
nos dice la intensidad del capital respecto a la mano de obra.

Lo interesante de esta función de producción es que por
más que la producción aumente, la intensidad del uso de los
factores se mantiene constante, es decir, solo varían las cantidades
de los recursos pero no la relación entre éstos.

Si despejamos "K" de la ecuación de la combinación
óptima de los factores, tendremos:

Esta ecuación se le denomina la senda de expansión porque
relaciona las cantidades de mano de obra y de capital que producen de manera
óptima dada la tecnología.

Se observa que esta ecuación es lineal lo que significa que
si aumenta el uso de la mano de obra, el uso del capital debe aumentar de
manera lineal para que la producción sea óptima. El ratio de
las productividades hace las veces de la pendiente de la ecuación lineal.
A continuación efectuamos el análisis gráfico.

Análisis gráfico

En la figura Nº 1 analizamos la función de producción
de coeficientes fijos.

Observamos que el punto "1" y "2" son óptimos
porque las combinaciones de capital y de mano de obra son las que corresponde
según el ratio de las productividades. La pendiente del rayo que parte
del origen o de la senda de expansión justamente tiene el ratio mencionado
anteriormente.

Las rectas azules que forman una letra "L", se denominan
"ISOCUANTAS", que son un conjunto de puntos que representan diferentes
combinaciones de capital y de mano de obra y estas combinaciones nos dan un
mismo nivel de producción. El punto "1" y "2" son
óptimos, pero el punto "3" y "4" no los son. En
el caso del punto "3", el capital es abundante y la mano de obra
sería el factor limitante y determinante para estimar cual será
la producción. En el caso del punto 4, el factor abundante es la mano
de obra y el factor limitante y determinante es el capital. De allí
que la función de producción use las letras MIN, de la palabra
MÍNIMO. En otras palabras, los dos factores de producción deben
ir combinados en base al ratio de las productividades.

Así, en esta función de producción, los recursos
se utilizan en combinaciones fijas. En otras palabras, conociendo el uso de
uno de los recursos, se sabrá fácilmente la cantidad que se
requiere del otro recurso, dada la senda de expansión.

Los Costos de Producción

Una vez definida la función de producción de largo plazo
y su respectiva senda de expansión, se hace necesario incluir los costos
en el presente análisis de largo plazo. Los costos de producción
son explicados por la siguiente ecuación, planteada anteriormente:

Por otro lado, tenemos que la senda de expansión es explicada
por la siguiente ecuación, igualmente planteada líneas arriba:

Si reemplazamos la senda de expansión en la ecuación
de costos, tendremos que:

Efectuando arreglos, tenemos:

Aquí tenemos los costos totales en función de la mano
de obra. De igual manera podemos reformular los costos totales en función
del capital:

Y los costos totales en función de la producción serán:

Que se obtiene de reemplazar cada uno de los componentes de la función
MIN de producción en la ecuación de los costos totales.

En la última ecuación tenemos que la cantidad de producto
es multiplicada por dos ratios. Cada uno de éstos, es el costo unitario
del respectivo recurso. Por ejemplo tenemos el caso de la mano de obra:

Si se resuelve el ratio de unidades obtenemos que las unidades finales
serán nuevos soles entre producto que no es nada más que un
costo unitario del recurso humano. Igual sucede para el recurso capital.

Entonces, la suma de los costos unitario de la mano de obra y del capital
nos dará el costo unitario total de todos los recursos, es decir, cada
factor contribuye en el costo unitario, que al ser multiplicado por la cantidad
de producto arrojará el costo total de producción.

En la figura Nº 2 se puede apreciar dos sendas de expansión,
con diferentes costos unitarios y por ende con diferentes tecnologías.

Vemos dos sendas de expansión, una más intensiva que
la otra en capital, o dicho de otra forma, una más intensiva en mano
de obra. La senda más empinada representa una tecnología más
intensiva en capital, y la senda más echada, es más intensiva
en mano de obra.

También en el gráfico se aprecia la restricción
presupuestal que es la ecuación de costos totales:

Despejando el capital, tenemos la restricción presupuestal:

A los largo de esta restricción presupuestaria, el costo es
el mismo, para diferentes combinaciones de recursos.

Si efectuamos el análisis en sentido diferente, si en la tecnología
más intensiva en capital, se aumenta una unidad de capital, la mano
de obra necesaria será menor si la comparamos con una tecnología
menos intensiva en capital. Esto significa que las inversiones en procesos
más intensivos en capital darán menos oportunidades al recurso
humano dada su naturaleza., Por otro lado, la expansión de las empresas
intensivas en mano de obra, generarán más empleo que la expansión
de las empresas más intensivas en capital.

Asumamos que la línea punteada de la figura de arriba es una
restricción presupuestaria inicial (recta "2"), y este presupuesto
se reduce y se convierte en la restricción presupuestal "1";
se aprecia que si esta reducción presupuestal es la misma para dos
empresas con diferentes tecnologías, cada una de estas empresas deberá
liberar más del recurso en la cual es más intensiva. Por ejemplo,
la empresa que es más intensiva en mano de obra liberará más
mano de obra que la empresa más intensiva en capital; y la empresa
más intensiva en capital, liberará más capital que la
empresa más intensiva en mano de obra. Es importante resaltar que la
reducción presupuestaria es la misma para ambas empresas, y esto se
hace con la finalidad de facilitar y aligerar la exposición.

Rendimientos a escala

La función de producción de coeficientes fijos presentan
rendimientos constantes a escala que significa que: "a medida que aumentan
en la misma proporción el uso de los recursos, el producto aumenta
en la misma proporción".

Sabemos que:

Y se incrementan lo recursos en el doble:

Apreciamos que el producto también aumenta en el doble.

Las economías a escala

Si se dobla el uso de los recursos, también aumentarán
los costos. En relación a la función de los costos totales:

Y poniendo esta ecuación en función del capital y la
mano de obra, tenemos que:

Si doblamos cada unos de los recursos:

Finalmente se observa que el costo también se dobla, es decir,
los costos aumentan en la misma proporción

Lo mismo observamos si utilizamos la función de los costos totales:

Si se dobla la producción, el costo total también aumentará
en la misma proporción.

En cuanto al costo medio o unitario, es explicada por la siguiente
ecuación:

Observamos que el costo unitario o medio es independiente de la cantidad
de recursos que se utilizan.

A continuación tenemos la figura Nº 3 donde una misma empresa
puede tener dos alternativas para producion

Vemos que la recta más empinada de la figura de costos totales
tiene una productividad menor debido a que los coeficientes tecnológicos
hacen que la pendiente sea mayor asumiendo que el costo de los recursos son
los mismos. En otras palabras, la tecnología es menos productiva porque
sus coeficientes son menores. Estos se verán reflejados en los costos
medios del gráfico inferior. La tecnología más productiva
tendrá menores costos medios.

Se puede concluir que la función de producción de coeficientes
fijos tiene la particularidad de que cuando aumenta la producción,
los costos medios se mantienen constantes lo que se denominan economías
constantes a escala.

El largo plazo es un "periodo suficientemente largo para que todos
los insumos sean variables". También se ha destacado otro aspecto
del largo plazo, quizás el más importante de todos. El largo
plazo es un horizonte de plantación. En efecto, cualquier producción,
cualquier actividad económica, ocurre en el corto plazo. El "largo
plazo" se refiere al hecho de que los agentes económicos -consumidores
y administradores- pueden planear para el futuro y seleccionar muchos aspectos
del "corto plazo" con que operan en el futuro. Por lo tanto, en
cierto sentido el largo plazo esta integrado por todas las situaciones posibles
del corto plazo entre las que puede elegir un agente económico.

Por ejemplo, antes de hacer una inversión, un gerente se encuentra
en una situación de largo plazo y podría seleccionar cualquiera
de una amplia variedad de inversiones diferentes. Una vez que se tome la decisión
de inversión y los fondos se congelan en el equipo de capital fijo,
la empresa opera en las condiciones del corto plazo. Así que quizás
la mejor distinción consista en decir que un agente económico
opera en el corto plazo y planea en el largo plazo.

El cálculo es muy sencillo. Cuando se produce una unidad del
bien, CFP es $100.00/1=$100.00. Cuando se producen dos unidades, CFP=$100.00/2=$50.00,
etc. En la grafica VIII3.2. Representamos el costo fijo promedio mediante
una curva CFP. El costo en pesos se mide en el eje vertical, y la producción
en el eje horizontal. La curva CFP tiene pendiente negativa en toda su extensión,
porque la razón del costo fijo respecto al volumen de producción
debe disminuir a medida que aumenta dicho volumen. Matemáticamente,
la curva CFP es una hipérbola rectangular.

Vayamos ahora a la columna (6) del cuadro. Esta columna lleva el nombre
de "costo variable promedio", un concepto enteramente analógico
al costo fijo promedio.

Cuadro VIII.3.2. Calculo del costo promedio y del costo marginal

Una empresa enfrenta normalmente una selección entre una amplia
variedad de plantas. En la grafica VIII.4.2 se muestran seis curvas de costo
promedio en el corto plazo; pero aun distan mucho de ser suficientes. Podrían
trazarse muchas curvas entre cada una de ellas. Estas seis plantas son solo
representativas de las muy diversas que podrían construirse.

Todas estas curvas generan una curva CPL como instrumento de plantación.
Supongamos que un empresario cree que la producción asociada al punto
A es la más rentable. Entonces construirá la planta representada
por CPC1, porque esta producirá esa cantidad al menor costo unitario
posible. Con la planta cuyo costo promedio en el corto plazo esta dado por
CPC1, el costo unitario podría reducirse aumentando la producción
hasta la cantidad asociada al punto B, que señala el nivel mínimo
de CPC1. Si cambiara de pronto las condiciones de la demanda, de modo que
resultara conveniente esta producción mayor, el empresario podría
expandirse sin dificultad, y aumentar su rentabilidad reduciendo el costo
unitario. Sin embargo, si elabora planes para el futuro, el empresario optaría
por construir la planta representada por CPC2, porque esta reduciría
más aun los costos unitarios. La planta operaria en el punto C, reduciendo
así el costo unitario por debajo del nivel del punto B de CPC1.

Resulta interesante observar que el punto B se encuentra donde la planta
de tipo 1 opera con mayor eficiencia (es decir, al menor coto unitario). Aun
así, conviene pasar a la planta de tipo 2, aunque esta no opere en
su nivel más eficiente. En efecto, todas las plantas menores que la
del tipo 4 se utilizan solo cuando están operando en un nivel menor
que el eficiente. La razón es que no es la eficiencia de una planta
dada lo que importa, sino la eficiencia global. Si la planta 1 puede ser remplazada
por la planta 2 y así se puede reducir el costo, carece de importancia
el hecho de que la planta 1 hubiese estado operando a su máxima eficiencia.
Puesto que en el punto A no se puede hacer un movimiento que reduzca los costos,
carece de importancia que A no sea tan eficiente como B. esta observación
se relaciona con la del ejemplo VII.3, pero no es la misma.

La curva de planeación en el largo plazo, CPL, es el lugar geométrico
de los puntos que representan el costo unitario mínimo de generar la
producción correspondiente. Así pues, esta es la curva de costo
promedio en el largo plazo. El empresario determina el tamaño de su
planta con referencia a esta curva, seleccionando la planta de corto plazo
que cause el menor costo unitario para el volumen esperado de producción.

Unidad V MODELOS DE MERCADO

Unidad V

Modelos de mercado

Objetivo educacional: Comprenderá los modelos de mercado,
analizándolos gráficamente, a través de la aplicación
del modelo matemático, para la toma de decisiones.

Actividades de aprendizaje.-

• Consultar los conceptos de competencia perfecta e imperfecta, monopolio,
  competencia oligopolica y monopolica.

• Investigar los modelos de mercado, identificando las características
  de cada uno de ellos, y citando ejemplos de los mismos, presentando los
  resultados de su investigación en material audiovisual.

• Resolver problemas de competencia perfecta, aplicando el enfoque
  total y marginal para lograr el equilibrio, mediante el análisis
  grafico.

• Aplicar el modelo matemático para la solución de
  problemas refentes a competencia perfecta y monopolio.

5.1 COMPETENCIA PERFECTA E IMPERFECTA

Competencia perfecta

El mercado de competencia perfecta es aquel en que existe un gran número
de compradores y vendedores de una mercancía; se ofrecen productos
similares (producto tipificado); existe libertad absoluta para los compradores
y vendedores y no hay control sobre los precios ni reglamentos para fijarlos.
Por ello el precio de equilibrio se da cuando la cantidad ofrecida es igual
a la cantidad demandada.

Las características o cuestiones que debe cumplen el mercado
para ser de competencia perfecta son:

• a) La oferta y la demanda deben ser anatómicas; es
  decir, constituidas por partes muy pequeñas. El número de
  oferentes y demandantes es tan grande, que ninguno de ellos en forma individual
  puede intervenir para modificar el precio.

• b) Debe existir plena movilidad de mercancías y factores
  productivos (tierra, trabajo, capital y organización); es decir,
  la posibilidad de moverse libremente en el mercado. Las empresas se comportan
  realmente como rivales, como autenticas competidoras.

• c) A las nuevas empresas que lo deseen y cuenten con recursos
  necesarios no se les debe impedir la entrada al mercado.

• d) Las mercancías deben ser homogéneas (producto
  tipificado). No debe haber diferencias específicas entre ellas
  para que no exista la necesidad de la publicidad competitiva, sino solamente
  informativa.

• e) Los poseedores de los factores productivos (demandantes
  y oferentes de mercancías y servicios) deben tener un perfecto
  conocimiento de todos los movimientos que ocurran en el mercado.

Algunos autores afirman que la competencia perfecta es diferente de
la competencia pura; por nuestra parte consideramos que ambas tienen las mismas
características y utilizamos los dos términos indistintamente.

El mercado de competencia perfecta o pura realmente no existe; mas
bien se puede afirmar que, en la medida en que un mercado con las características
señaladas será mas perfecto o bien, en la medida en que no cumpla
con dichas características, será menos perfecto o se alejara
de la perfección (mercado de competencia imperfecta).

Sin embargo, es necesario conocer el mercado de competencia perfecta
aunque no opere en la realidad. Porque esto nos permitirá ir comparando
y analizando las imperfecciones de los mercados que deseamos estudiar.

En la competencia perfecta el precio se fija cuando la oferta y la
demanda son las mismas; el punto donde coinciden la oferta y la demanda se
conocen como precio de equilibrio.

Gráficamente el precio de equilibrio se representa como en la
figura 5-22.

No hay que olvidar que la oferta y la demanda representan intereses
contrarios (fuerzas opuestas ya que los ofertantes desean vender más
a un precio mas alto para obtener mayores ganancias y los demandantes desean
comprar mas a un precio mas bajo para obtener mayor satisfacción).

Un ejemplo de cómo se forma el precio de equilibrio es el siguiente:
dada una tabla de oferta y demanda, obtenga el precio de equilibrio y grafiquelo
(fig. 5-23).

El precio de equilibrio es 12, ya que en este punto se igualan la oferta
y la demanda. Debajo de este precio hay demanda excesiva en relación
con la oferta y oferta insuficiente en relación con la demanda. Arriba
de ese precio la demanda es insuficiente en relación con la oferta
y la oferta es excesiva en relación con la demanda. La cantidad de
equilibrio es 120.

El precio del equilibrio tiende a mantenerse siempre y cuando no varíen
la demanda y la oferta; si estas sufren modificaciones, el precio de equilibrio
cambia. Es decir, en competencia perfecta el precio depende del libre movimiento
de la demanda y la oferta.

Competencia imperfecta

Hemos visto las características de un mercado de competencia
perfecta y hemos observado que no se da en la realidad; entonces, ¿Qué
tipo de mercado existe realmente?

Existe una gran diversidad de mercados que operan en la economía
y que desde el punto de vista de la competencia se han agrupado como mercado
de competencia imperfecta.

¿Qué característica tiene un mercado de competencia
imperfecta?

En la medida en que determinado mercado no cumpla con las características
de la competencia perfecta, se alejara de ella o bien será un mercado
con mayor o menor imperfección u con mayor o menor competencia. Por
lo tanto, algunas características de la competencia imperfecta son:

• a) El numero de oferentes no es tan grande como en la competencia
  perfecta; puede ser un reducido numero o bien un solo vendedor. En este
  caso los oferentes si pueden intervenir para modificar los precios.

• b) No existe plena movilización de mercancías
  y factores productivos. Es decir, existe o puede existir algún
  grado de control sobre las mercancías o los factores productivos.

• c) Puede haber diferencia de productos (los productos no son
  homogéneos). Debido a estas diferencias (reales o supuestas) de
  las mercancías puede existir la publicidad competitiva.

• d) No hay plena libertad para que nuevos oferentes entren
  al mercado, ya que puede haber control de patente control de patentes,
  control tecnológico, etc.

• e) No existe perfecto conocimiento de todos los movimientos
  que ocurren en el mercado sobre todo de los demandantes. Es posible que
  los oferentes conozcan mejor los movimientos del mercado aunque no en
  forma perfecta.

5.2 COMPETENCIA PURA Y PERFECTA

Las condiciones

La competencia pura y perfecta es un modelo de la teoría económica
de la escuela neoclásica que describe una estructura de mercado hipotética
en la cual ningún productor ni consumidor dispone de poder para fijar
los precios ni sobre las decisiones de los demás agentes, y además
todos tienen el mismo acceso a la información, lo que supone una igualdad
de las posiciones de origen en la relación mercantil. El precio es
entonces fijado por el afrontamiento y la negociación de todos con
todos, sin generar renta de monopolio. La competencia pura y perfecta representa
uno de los dos casos extremos de estructuras de mercado estudiadas por los
economistas neoclásicos, el segundo es el caso del monopolio. Se supone
que la competencia perfecta permite el equilibrio sobre todos los mercados
bajo unas condiciones suficientes muy particulares. Cada mercado debe cumplir
las tres condiciones siguientes:

• La atomicidad del mercado: el número de compradores
  y de vendedores es muy amplio, con lo cual la oferta o la demanda de cada
  agente es sin importancia con respecto a la oferta o demanda total.

• La homogeneidad de los productos: los bienes intercambiados
  son similares en calidad y características; un producto de mejor
  calidad constituye entonces otro mercado. En la realidad, los bienes más
  homogéneos son las materias primas y los productos de la agricultura.

Partes: 1, 2, 3, 4