La ley de los grandes números

Puesto que el evento Z = z es la unión del par de eventos
disjuntos: (X = k) e (Y = z – k), tendremos:
Decimos que p3(x) es la convolución de p1(x) y p2(x):
p3(x) = p1(x) * p2(x)

2
Convolución
La convolución es una operación conmutativa y asociativa.

Visto lo visto, es "fácil" demostrar por inducción cómo será
la suma de n variables aleatorias independientes:
teniendo en cuenta que:

3
Veamos un ejemplo: Supongamos que lanzamos un dado
dos veces. Sea el resultado del primer lanzamiento la variable
aleatoria X1 y del segundo, la variable aleatoria X2 , ambas
con la misma distribución de probabilidad que llamaremos
m(x). Calculemos la función de distribución de probabilidad
para S2 = X1 + X2.
(….)

4
Si quisiéramos calcular S3 = X1 + X2 + X3 , tendríamos:
(…)
Este es el resultado
gráfico para la suma
S10 de 10 dados.

5
Y estos son los resultados
gráficos para las sumas
S20 y S30 de 20 y 30 dados,
respectivamente.

Observemos que, a medida
que aumenta el número
de dados, tenemos una
curva que se aproxima
más y más a una campana
de Gauss, a una normal.

Veremos por qué más
adelante, cuando hablemos
del teorema central del
límite.

6
Suma de variables aleatorias continuas
Si X e Y son dos variables aleatorias continuas e
independientes con funciones densidad de probabilidad
f(x) y g(x) respectivamente, la variable aleatoria Z = X + Y,
tendrá como densidad de probabilidad la convolución
de f y g:

7
Suma de dos variables aleatorias uniformes
independientes
Dos distribuciones
uniformes U(0,1).
Obtenemos la
densidad de
probabilidad de la
suma de las dos
variables por
convolución de sus
densidades.

8
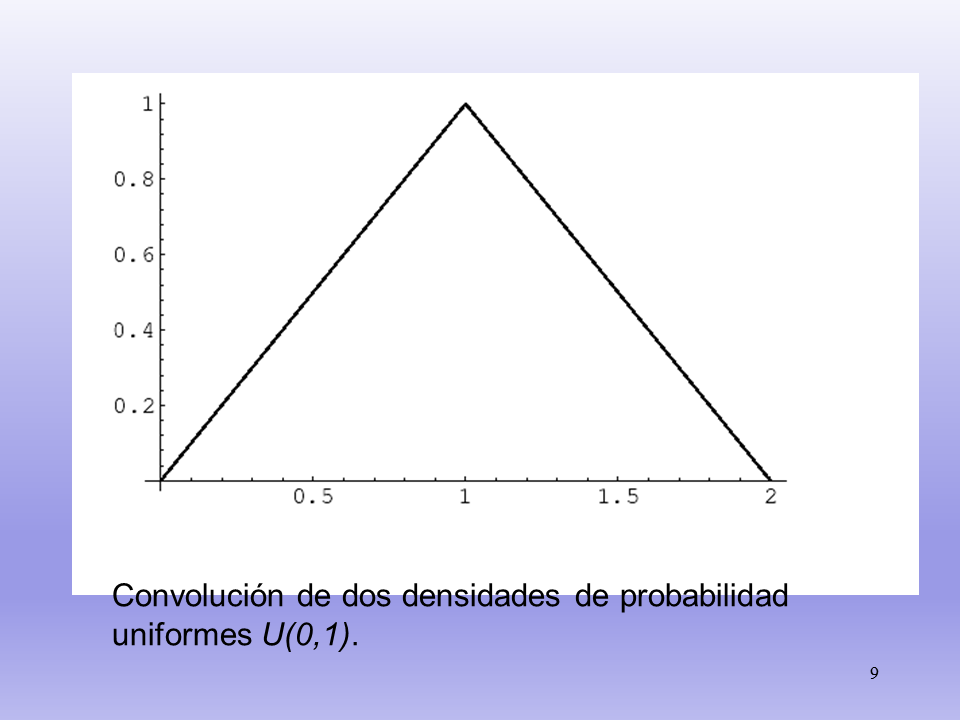
Observa que, como X e Y varían entre 0 y 1, su suma Z variará entre 0 y 2.

9
Convolución de dos densidades de probabilidad
uniformes U(0,1).

10
Suma de dos variables aleatorias
exponenciales independientes
Dos densidades
de probabilidad
exponenciales
Exp(?).
Obtenemos la
densidad de
probabilidad de la
suma de las dos
variables por
convolución de sus
densidades.