
HISTORIA
TÉCNICAS DE DETECCIÓN DE ERRORES
TÉCNICAS DE CORRECCIÓN DE ERRORES
RICHARD WESLEY HAMMING
CÓDIGO HAMING
CORRECCIÓN DE ERRORES
SÍNDROME Y CORRECCIÓN DE ERROR
DETECCIÓN Y EFICIENCIA SOBRE CANAL
HAMING EXTENDIDO
CONCLUSIONES
BIBLIOGRAFÍA
CONTENIDO

Cuando se transmite información, se corre el riesgo de la presencia de interferencia o ruido.
El origen de la teoría de códigos correctores de errores se encuentra en los trabajos de Golay, Hamming y Shannon.
Inicio enfoque probabilístico, pasa a un enfoque más algebraico [códigos de Golay y de Hamming, los códigos cíclicos y BCH, o los códigos de Reed-Solomon y de Reed-Muller].
HISTORIA

En los 70 Goppa – Construye códigos lineales a partir de curvas algebraicas lisas llamados códigos AG (álgebro-geométricos).
Los códigos AG apenas han sido implementados en la práctica debido a la profundidad matemática de las ideas subyacentes.
Los métodos de decodificación para códigos geométricos de Goppa son efectivos, su preprocesamiento es de una elevada dificultad e involucra complejos algoritmos basados en métodos de la geometría algebraica computacional.
HISTORIA

Códigos VRC (Vertical Redundancy Check).
En esta técnica, un bit redundante, denominado bit de paridad, se añade al final de cada bloque de datos.
Código LRC (Longitudinal Redundancy Check).
Esta técnica consiste en VRC de dos dimensiones, se agrupa un determinado número de unidades de datos en un bloque, cada uno con su bit VRC correspondiente. Se calcula el bit de paridad entre cada bit de todas y cada una de las unidades de datos (primeros bits, segundos, etc.). Se reúnen los bits de paridad de todas las posiciones en una nueva unidad de datos y se añade al final del bloque.
TÉCNICAS DE DETECCIÓN DE ERRORES

Comprobación de redundancia cíclica (CRC).
Dado un bloque o mensaje de k bits, el transmisor genera una secuencia de n bits, denominada secuencia de comprobación de trama (FCS Frame Check Sequence), la trama resultante, de n + k bits sea divisible por algún número predeterminado (patrón de bits). El receptor dividirá la trama recibida por el mismo patrón de bits y, si el resto en la división (resto 0), indica que la transmisión ha sido correcta, sin error.
TÉCNICAS DE DETECCIÓN DE ERRORES

Requerimiento automático de repetición (ARQ)
Pare y espere ( stop and wait ARQ ): Cuando el receptor recibe una trama procede a validarla, si no contiene errores envía una señal de confirmación hacia el emisor ACK (acknowledge). Si hay error envía una señal de recepción errónea llamada NAK (negative acknowledge).
Envío continuo ( Continuos ARQ ): Presenta el inconveniente de reducir el tiempo de utilización efectiva de los canales de comunicación dado que cada mensaje debe ser confirmado individualmente y todo se paraliza hasta que ello ocurre.
TÉCNICAS CORRECCIÓN DE ERRORES

Corrección de errores hacia adelante (FEC)
Códigos de bloque: Un código de bloques convierte k bits de entrada en n bits de salida con n>k, este es un código sin memoria.
Códigos de árbol: Un código de árbol es producido por un codificador con memoria, a este grupo pertenecen los códigos convolucionales, los cuales tienen como característica que a cada bit de una secuencia se le aplica una operación binaria especifica.
TÉCNICAS CORRECCIÓN DE ERRORES

Richard Wesley Hamming
Programó el computador que realizo los campos para la 1ra. Bomba Atómica.
1950 Trabajando en los laboratorios Bell junto a Shannon, desarrolló y público la teoría de codificación.
Fue el Precursor de los lenguajes de programación de alto nivel.
Su descubrimiento fue uno de los más importantes en la ciencia de la informática.
Su método permite identificar un bit erróneo en una palabra codificada (en binario). Esto es, si un bit es incorrecto, por ejemplo: el cambio de un 1 por un 0 en una transmisión, podemos no solo detectar el bit erróneo, sino además corregirlo.

CÓDIGO HAMING
Es un código que se utiliza en la detección y corrección de errores que se producen en la transmisión de códigos binarios, la palabra de código se conforma por los bits de comprobación y los bits de información.
Las distancia mínima de Haming está dada por la siguiente ecuación:
Dm= 2X+1
Donde Dm es la distancia mínima de un código para permitir la corrección de datos y X es las líneas de datos.
n: número de bits del código original que se pretende transmitir.
p: número de bits de paridad par generados en el transmisor, o sea, número de líneas que añadimos al código inicial.
c: número de bits detectores de paridad par generados por el receptor.

CÓDIGO HAMING
Combinaciones posibles
Orden para asignar combinaciones
Combinación asignada a la situación en que no haya error en la transmisión.
Combinaciones asignadas a los bits de paridad generados en el transmisor.
Combinaciones asignadas a los bits de datos del código original.
Notación (k,n)
n = número de bits de información
h = número de bits de la cadena = 2c -1
La notación sería la siguiente (h,n)

CÓDIGO HAMING
Combinaciones posibles
Orden para asignar combinaciones
Combinación asignada a la situación en que no haya error en la transmisión.
Combinaciones asignadas a los bits de paridad generados en el transmisor.
Combinaciones asignadas a los bits de datos del código original.
Notación (k,n)
n = número de bits de información
h = número de bits de la cadena = 2c -1
La notación sería la siguiente (h,n)
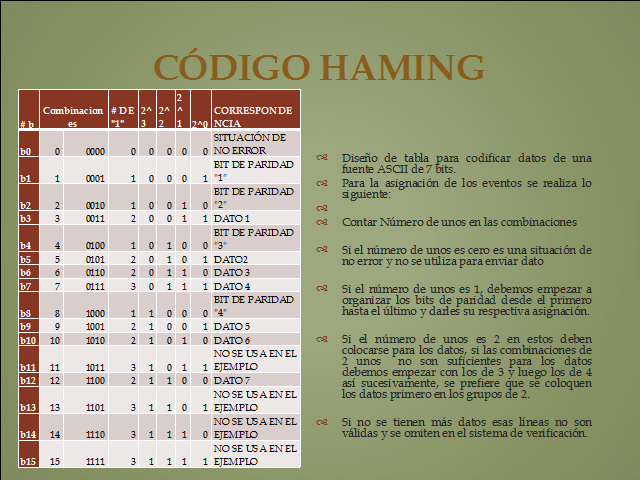
CÓDIGO HAMING
Diseño de tabla para codificar datos de una fuente ASCII de 7 bits.
Para la asignación de los eventos se realiza lo siguiente:
Contar Número de unos en las combinaciones
Si el número de unos es cero es una situación de no error y no se utiliza para enviar dato
Si el número de unos es 1, debemos empezar a organizar los bits de paridad desde el primero hasta el último y darles su respectiva asignación.
Si el número de unos es 2 en estos deben colocarse para los datos, si las combinaciones de 2 unos no son suficientes para los datos debemos empezar con los de 3 y luego los de 4 así sucesivamente, se prefiere que se coloquen los datos primero en los grupos de 2.
Si no se tienen más datos esas líneas no son válidas y se omiten en el sistema de verificación.
Página siguiente  |