Análisis de algoritmos II (página 2)

Partes: 1, 2

1. Introducción.
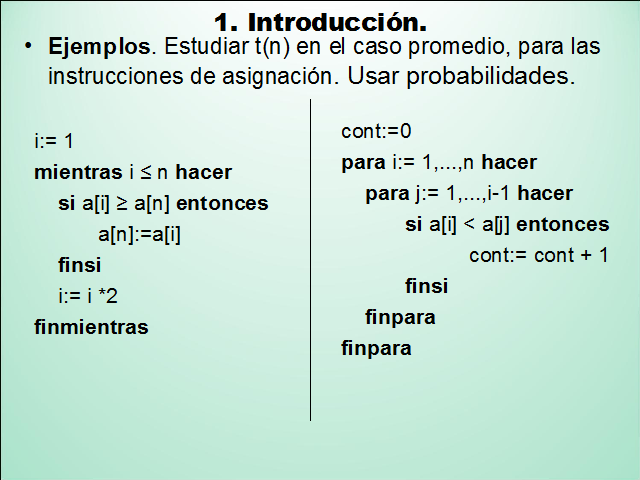
Ejemplos. Estudiar t(n) en el caso promedio, para las instrucciones de asignación. Usar probabilidades.
cont:=0
para i:= 1,…,n hacer
para j:= 1,…,i-1 hacer
si a[i] < a[j] entonces
cont:= cont + 1
finsi
finpara
finpara
i:= 1
mientras i = n hacer
si a[i] = a[n] entonces
a[n]:=a[i]
finsi
i:= i *2
finmientras

1. Introducción.
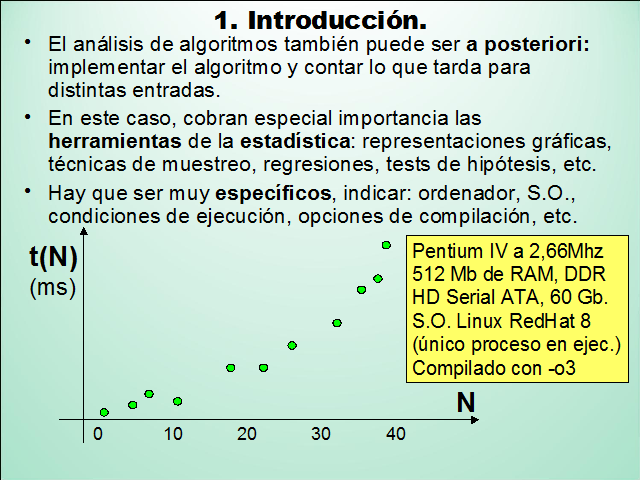
El análisis de algoritmos también puede ser a posteriori: implementar el algoritmo y contar lo que tarda para distintas entradas.
En este caso, cobran especial importancia las herramientas de la estadística: representaciones gráficas, técnicas de muestreo, regresiones, tests de hipótesis, etc.
Hay que ser muy específicos, indicar: ordenador, S.O., condiciones de ejecución, opciones de compilación, etc.
N
t(N) (ms)
0
10
20
30
40
Pentium IV a 2,66Mhz
512 Mb de RAM, DDR
HD Serial ATA, 60 Gb.
S.O. Linux RedHat 8
(único proceso en ejec.)
Compilado con -o3

1. Introducción.
Indicamos los factores externos, porque influyen en los tiempos (multiplicativamente), y son útiles para comparar tiempos tomados bajo condiciones distintas.
La medición de los tiempos es un estudio experimental.
El análisis a posteriori suele complementarse con un estudio teórico y un contraste teórico/experimental.
c1n2 + c2n + c3
N
t(N)
0
10
20
30
40
Ejemplo. Haciendo el estudio teórico del anterior programa, deducimos que su tiempo es de la forma: c1n2 + c2 n + c3
Podemos hacer una re-gresión. ? ¿Se ajusta bien? ¿Es correcto el estudio teórico?

1. Introducción.
El contraste teórico/experimental permite: detectar posibles errores de implementación, hacer previsiones para tamaños inalcanzables, comparar implementaciones.
Sin el estudio teórico, extraer conclusiones relevantes del tiempo de ejecución puede ser complejo.
Ejemplo. Programa
“cifras.exe”:
N= 4, T(4)= 0.1 ms
N= 5, T(5)= 5 ms
N= 6, T(6)= 0.2 s
N= 7, T(7)= 10 s
N= 8, T(8)= 3.5 min

¿Qué conclusiones podemos extraer?
El análisis a priori es siempre un estudio teórico previo a la implementación. Puede servir para evitar la implementación, si el algoritmo es poco eficiente.
N
t(N) (ms)

2. Notaciones asintóticas.
El tiempo de ejecución t(n) está dado en base a unas constantes que dependen de factores externos.
Nos interesa un análisis que sea independiente de esos factores.
Notaciones asintóticas: Indican como crece t, para valores suficientemente grandes (asintóticamente) sin considerar constantes.
O(t): Orden de complejidad de t.
?(t): Orden inferior de t, u omega de t.
?(t): Orden exacto de t.

2.1. Definiciones.
Orden de complejidad de f(n): O(f)
Dada una función f: N ? R+, llamamos orden de f al conjunto de todas las funciones de N en R+ acotadas superiormente por un múltiplo real positivo de f, para valores de n suficientemente grandes.

O(f)= { t: N ? R+ / ? c ? R+, ? n0 ? N, ? n ? n0; t(n) ? c·f(n) }

2.1. Definiciones.
Observaciones:
O(f) es un conjunto de funciones, no una función.
“Valores de n suficientemente grandes…”: no nos importa lo que pase para valores pequeños.
“Funciones acotadas superiormente por un múltiplo de f…”: nos quitamos las constantes multiplicativas.
La definición es aplicable a cualquier función de N en R, no sólo tiempos de ejecución.

2.1. Definiciones.
N
R+
c·f(n)
O(f)

2.1. Definiciones.
Uso de los órdenes de complejidad
1) Dado un tiempo t(n), encontrar la función f más simple tal que t ? O(f), y que más se aproxime asintóticamente.
Ejemplo. t(n) = 2n2/5 + 6n + 3?·log2 n + 2 ? t(n) ? O(n2)

2) Acotar unafunción difícilde calcularcon precisión.

Ejemplo.t(n) ? O(f(n))

2.1. Definiciones.
Uso de los órdenes de complejidad
3) Acotar una función que no tarda lo mismo para el mismo tamaño de entrada (distintos casos, mejor y peor).

Ejemplo.t(n) ? O(tM(n))
Igual que con la cota superior, podríamos hacer con la cota inferior…

2.1. Definiciones.
Relación de orden entre O(..) = Relación de inclusión entre conjuntos.
O(f) ? O(g) ? O(f) ? O(g) ? Para toda t ? O(f), t ? O(g)

Se cumple que:
O(c) = O(d), siendo c y d constantes positivas.
O(c) ? O(n)
O(cn + b) = O(dn + e)
O(p) = O(q), si p y q son polinomios del mismo grado.
O(p) ? O(q), si p es un polinomio de menor grado que q.

2.1. Definiciones.
N
R+
c·f(n)
O(f)
d·g(n)
O(g)
O(g) ? O(f)

2.1. Definiciones.
Orden inferior u omega de f(n): ?(f)
Dada una función f: N ? R+, llamamos omega de f al conjunto de todas las funciones de N en R+ acotadas inferiormente por un múltiplo real positivo de f, para valores de n suficientemente grandes.

?(f)= { t: N ? R+ / ? c ? R+, ? n0 ? N, ? n ? n0; t(n) ? c·f(n) }

2.1. Definiciones.
N
R+
c·f(n)
?(f)
La notación omega se usa para establecer cotas inferiores del tiempo de ejecución.
Relación de orden: igual que antes, basada en la inclusión.

2.1. Definiciones.
Orden exacto de f(n): ?(f)
Dada una función f: N ? R+, llamamos orden exacto de f al conjunto de todas las funciones de N en R+ que crecen igual que f, asintóticamente y salvo constantes.

?(f) = O(f) ? ?(f) =
= { t: N ? R+ / ? c, d ? R+, ? n0 ? N, ? n ? n0; c·f(n) ? t(n) ? d·f(n) }

2.1. Definiciones.
Si un algoritmo tiene un t tal que t ? O(f) y t ? ?(f), entonces t ? ?(f).
R+
f(n)
?(f)
N

2.1. Definiciones.
Ejemplos. ¿Cuáles son ciertas y cuáles no?
3n2 ? O(n2) n2 ? O(n3) n3 ? O(n2)
3n2 ? ?(n2) n2 ? ?(n3) n3 ? ?(n2)
3n2 ? ?(n2) n2 ? ?(n3) n3 ? ?(n2)
2n+1 ? O(2n) (2+1)n ? O(2n) (2+1)n ? ?(2n)
O(n) ? O(n2) (n+1)! ? O(n!) n2 ? O(n!!)

2.1. Definiciones.
Notación o pequeña de f(n): o(f)
Dada una función f: N ? R+, llamamos o pequeña de f al conjunto de todas las funciones de N en R+ que crecen igual que f asintóticamente:

o(f)= { t: N ? R+ / lim t(n)/f(n) = 1}
n??

Esta notación conserva las constantes multiplicativas para el término de mayor orden.

2.1. Definiciones.
Notación o pequeña de f(n): o(f)

Ejemplo. t(n) = amnm + am-1nm-1 + … +a1n + a0
t(n) ? o(amnm) ? o(nm)

t(n) = 3,2n2 + 8n – 9 ? o(¿?)
t(n) = 82 n4 + 3·2n + 91 log2 n ? o(¿?)
t(n) = 4n3 + 3n3 log2 n – 7n2 + 8 ? o(¿?)
¿o(t) ? O(t)?

2.2. Propiedades de las notaciones asintóticas.
P1. Transitividad.Si f ? O(g) y g ? O(h) entonces f ? O(h).

Si f ? ?(g) y g ? ?(h) entonces f ? ?(h)
Ej. 2n+1 ? O(n), n ? O(n2) ? 2n+1 ? O(n2)

P2. Si f ? O(g) entonces O(f) ? O(g).

¿Cómo es la relación para los ??

2.2. Propiedades de las notaciones asintóticas.
P3. Relación pertenencia/contenido.Dadas f y g de N en R+, se cumple:
i) O(f) = O(g) ? f ? O(g) y g ? O(f)
ii) O(f) ? O(g) ? f ? O(g)

¿La relación de orden entre O(..) es completa? Dadas f y g, ¿se cumple O(f)?O(g) ó O(g)?O(f)?

2.2. Propiedades de las notaciones asintóticas.
P4. Propiedad del máximo.Dadas f y g, de N en R+, O(f+g) = O(max(f, g)).

Con omegas: ?(f+g) = ?(max(f, g))
¿Y para los ?(f+g)?
¿Es cierto que O(f – g) = O(max(f, -g))?
Ejemplo: O(2n + n6 + n!) = …

¿Qué relación hay entre O(log2 n) y O(log10 n)?

2.2. Propiedades de las notaciones asintóticas.
P5. Equivalencia entre notaciones.Dadas f y g de N en R+, O(f)=O(g) ? ?(f)=?(g) ? f ? ?(g) ? ?(f)=?(g)

P6. Relación límites/órdenes.Dadas f y g de N en R+, se cumple:
i) limn?? f(n) ? R+ ? O(f) = O(g)
g(n)
ii) limn?? f(n) = 0 ? O(f) ? O(g)
g(n)
iii) limn?? f(n) = +? ? O(f) ? O(g)
g(n)

2.3. Notaciones con varios parámetros.
En general, el tiempo y la memoria consumidos pueden depender de muchos parámetros.
f: Nm ? R+ (f: Nx…m..xN ? R+)

Orden de complejidad de f(n1, n2, …, nm): O(f)
Dada una función f: Nm ? R+, llamamos orden de f al conjunto de todas las funciones de Nm en R+ acotadas superiormente por un múltiplo real positivo de f, para valores de (n1, …, nm) suficientemente grandes.

O(f)= { t: Nm ? R+ / ? c ? R+, ? n1, n2, .., nm ? N, ? k1 ? n1 ,
? k2 ? n2 ,..,? km ? nm; t(k1, k2, …, km) ? c·f(k1, k2, …, km) }

2.3. Notaciones con varios parámetros.
Ejemplo. Tiempo de ejecución de la BPP con listas de adyacencia: O(n+a).Memoria usada en una tabla hash: depende del número de cubetas, elementos, tamaño de celda…

Podemos extender los conceptos de ?(f) y ?(f), para funciones con varios parámetros.
Las propiedades se siguen cumpliendo ? Demostrarlo.
¿Qué relación hay entre los siguientes órdenes?
O(n+m), O(nm) O(n2), O(n+2m)

2.4. Notaciones condicionales.
En algunos casos interesa estudiar el tiempo sólo para ciertos tamaños de entrada.
Ejemplo. Algoritmo de búsqueda binaria: Si N es potencia de 2 el estudio se simplifica.

Orden condicionado de f(n): O(f | P)
Dada una función f: N ? R+, y P: N ? B, llamamos orden de f según P (o condicionado a P) al conjunto:
O(f | P)= { t: N ? R+ / ? c ? R+, ? n0 ? N, ? n ? n0;
P(n) ? t(n) ? c·f(n) }

2.4. Notaciones condicionales.
De igual forma, tenemos ?(f | P) y ?(f | P).

Ejemplo.
Si estudiamos el tiempo para tamaños de entrada que sean potencia de 2:t(n) ? O(f | n = 2k)
Para tamaños que sean múltiplos de 2:
t(n) ? O(f | n = 2k)

O(f) = O(f | true).
Para cualquier f y g, f ? O(g | false).
¿O(f) ? O(f | P)?

2.5. Cotas de complejidad frecuentes.
Algunas relaciones entre órdenes frecuentes.
O(1) ? O(log n) ? O(n) ? O(n·log n) ?
O(n·(log n)2) ? O(n1.001…) ? O(n2) ? O(n3) ? …
? O(2n) ? O(n!) ? O(nn)

¿Dónde va O(3n)? ¿Y O(n3 2n)?
¿Qué pasa con las omegas? ¿Y con los órdenes exactos?

2.5. Cotas de complejidad frecuentes.
El orden de un polinomio anxn+…+a1x+a0 es O(xn).

n n n
?1 ? O(n); ?i ? O(n2) ?im ? O(nm+1)
i=1 i=1 i=1
Si hacemos una operación para n, otra para n/2, n/4, …, aparecerá un orden logarítmico O(log2 n).

Los logaritmos son del mismo orden, independien-temente de la base. Por eso, se omite normalmente.

Sumatorios: se pueden aproximar con integrales, una acotando superior y otra inferiormente.

Casos promedios: usar probabilidades.

3. Ecuaciones de recurrencia.
Es normal que un algoritmo se base en procedimientos auxiliares, haga llamadas recursivas para tamaños menores o reduzca el tamaño del problema progresivamente.
En el análisis, el tiempo t(n) se expresa en función del tiempo para t(n-1), t(n-2)…? Ecuaciones de recurrencia.

Ejemplo. ¿Cuántas operaciones mover se ejecutan?
Hanoi (n, i, j, k)
if n>0 then
Hanoi (n-1, i, k, j)
mover (i, j)
Hanoi (n-1, k, j, i)
else
mover (i, j)

3. Ecuaciones de recurrencia.
En general, las ecuaciones de recurrencia tienen la forma:

t(n) = b Para 0 ? n ? n0 Casos base
t(n) = f (t(n), t(n-1), …, t(n-k), n) En otro caso

Tipos de ecuaciones de recurrencia:
Lineales y homegéneas:
a0t(n) + a1t(n-1) + … + akt(n-k) = 0
Lineales y no homegéneas:
a0t(n) + a1t(n-1) + … + akt(n-k) = p(n) + …
No lineales:
Ejemplo: a0t2(n) + t(n-1)*t(n-k) + sqrt(t(n-2) + 1) = p(n)

3.1. Ecuaciones lineales homogéneas.
La ecuación de recurrencia es de la forma:
a0t(n) + a1t(n-1) + … + akt(n-k) = 0; ai constante

Caso sencillo:
1 Si n = 0
t(n) =
x·t(n-1) Si n > 0

Solución: t(n) = xn

3.1. Ecuaciones lineales homogéneas.
Suponiendo que las soluciones son de la forma t(n) = xn, la ecuación de recurrencia homogénea:
a0t(n) + a1t(n-1) + … + akt(n-k) = 0

Se transforma en:
a0xn + a1xn-1 + … + akxn-k = 0 ? /xn-k ?
a0xk + a1xk-1 + … + ak = 0

Ecuación característica de la ecuación recurrente lineal homogénea

3.1. Ecuaciones lineales homogéneas.
a0xk + a1xk-1 + … + ak = 0
Ecuación característica de la ecuación recurrente lineal homogénea

k: conocida. ai: conocidas. x: desconocida.
Resolver el sistema para la incógnita x. El resultado es:
t(n) = xn
Pero… Un polinomio de grado k tendrá k soluciones…

3.1. Ecuaciones lineales homogéneas.
Sean las soluciones x= (s1, s2, …, sk), todas distintas.
La solución será:
k
t(n) = c1·s1n + c2·s2n + … + ck·skn = ? ci·sin
i=1
Siendo ci constantes, cuyos valores dependen de los casos base (condiciones iniciales).

Son constantes que añadimos nosotros. Debemos resolverlas, usando los casos base de la ecuación recurrente.

3.1. Ecuaciones lineales homogéneas.
Ejemplo. El tiempo de ejecución de un algoritmo es:
0 Si n = 0
t(n) = 1 Si n = 1
3·t(n-1) + 4·t(n-2) Si n > 1

Encontrar una fórmula explícita para t(n), y calcular el orden de complejidad del algoritmo.

¿Qué pasa si no todas las soluciones son distintas?

3.1. Ecuaciones lineales homogéneas.
Si no todas las soluciones x= (s1, s2, …, sk) son distintas, entonces el polinomio característico será:
a0xn + a1xn-1 + … + akxn-k = (x – s1)m·(x – s2)·…(x – sp)·xn-k

¿Cuál es la solución para t(n)?

Las derivadas valen 0 en s1, hasta la m-1-ésima.

a0n·xn-1 + a1(n-1)·xn-2 + … + ak(n-k)·xn-k-1 = 0 ? ·x ?
a0n·xn + a1(n-1)·xn-1 + … + aK(n-k)xn-k = 0

3.1. Ecuaciones lineales homogéneas.
Las derivadas valen 0 en s1, hasta la m-1-ésima.

Conclusión: t(n) = n·s1n también será solución de la ecuación característica.

Para la segunda derivada: t(n) = n2s1n será solución…

Si si tiene multiplicidad m, entonces tendremos:
sin n·sin n2·sin … nm-1·sin

3.1. Ecuaciones lineales homogéneas.
Dadas las soluciones x= (s1, s2, …, sk) siendo sk de multiplicidad m, la solución será:

t(n) = c1·s1n + c2·s2n + … + ck·skn + ck+1·n·skn +
+ ck+2·n2·skn + … + ck+1+m·nm-1·skn

Ejemplo. Calcular t(n) y el orden de complejidad para:
t(n) = 5 t(n-1) – 8 t(n-2) + 4 t(n-3)
t(0) = 0, t(1) = 3, t(2) = 10

3.2. Recurrencias no homogéneas.
¿Qué pasa si tenemos algo como t(n) = 2·t(n-1) + 1?

Términos que no tienen t(x) ? Recurrencia no homogénea.

Ejemplo. Calcular t(n) para: t(n) = 2t(n-1) + 3n(n+1)
t(n) – 2t(n-1) = 3n(n+1) ?
t(n+1) – 5t(n) + 6t(n-1) = 3n+1 ?
t(n+2) – 8t(n+1) + 21t(n) – 18t(n-1) = 0 ?

Ecuación característica: (x-2)(x-3)2 = 0

3.2. Recurrencias no homogéneas.
Conclusión: Si en la ecuación de recurrencia aparece un término de la forma bn·p(n) (p(n) polinomio de n), entonces en la ecuación característica habrá un factor:

(x-b)Grado(p(n))+1 ? Sol. b con multiplicidad Grado(p(n))+1

Ejemplo: t(n) – t(n-3) = 2 + n3 + n2·3n + 2(n+1) + 8n2
¿Cuál es la ecuación característica?

3.2. Recurrencias no homogéneas.
En general, tendremos recurrencias de la forma:
a0t(n) + a1t(n-1) + … + akt(n-k) = b1np1(n) + b2np2(n) + …

Y la ecuación característica será:
(a0xk + a1xk-1 + … + ak)(x-b1)G(p1(n))+1(x-b2)G(p2(n))+1… = 0

Ejemplo. Calcular t(n) y O(t(n)).
t(n) = 1 + n n = 0, 1
t(n) = 4t(n-2) + (n+5)3n + n2 Si n>1

3.3. Cambio de variable.
t(n) = a·t(n/4) + b·t(n/8) + ….

Cambio de variable:
Convertir las ecuaciones anteriores en algo de la forma t’(k) = a·t’(k-c1) + b·t’(k-c2) + …
Resolver el sistema en k.
Deshacer el cambio, y obtener el resultado en n

Cambios típicos:
n = 2k; k = log2 n ? n = 3k, k = log3 k
n= 5k; k = n/5

3.3. Cambio de variable.
Ejemplo 1. Resolver:
t(n) = a Si n=1
t(n) = 2 t(?n/2?) + b·n Si n>1, con b>0

Ejemplo 2. Resolver:
t(n) = n Si n< b
t(n) = 3·t(n-b) + n2 + 1 En otro caso

3.3. Cambio de variable.
Los órdenes que obtenemos son condicionados a que se cumplan las condiciones del cambio: t(n) ? O(f | P(n))
¿Cómo quitar la condición?

Teorema. Sea b un entero ? 2, f: N ? R+ una función no decreciente a partir de un n0 (f es eventualmente no decreciente) y f(bn) ? O(f(n)) (f es b-armónica) y t: N ? R+ eventualmente no decreciente. Entonces, si t(n) ? ?(f(n) | n=bk) se cumple que t(n) ? ?(f(n)).

3.4. Otras técnicas.
Transformación de la imagen
Se utiliza en algunos casos, donde las ecuaciones recurrentes son no lineales. Ejemplo.
t(1) = 6; t(n) = n t2(n/2)
Suponiendo n potencia de 2, hacemos el cambio n=2k:
t(20) = 6; t(2k) = 2k t2(2k-1)
Tomando logaritmos (en base 2):
log t(20) = log 6; log t(2k) = k + 2·log t(2k-1)
Se hace una transformación de la imagen:
v(x) = log t(2x) ?
v(0) = log 6; v(k) = k + 2·v(k-1)

3.4. Otras técnicas.
Transformación de la imagen
Resolver la ecuación recurrente:
v(0) = log 6; v(k) = k + 2·v(k-1)
Resultado:
v(k)= c1·2k + c2 + c3·k ? v(k) = (3+log 3)·2k – k – 2
Ahora deshacer el cambio v(x) = log t(2x):
log t(2k) = log t(n) = (3+log 3)·2k – k – 2
Y quitar los logaritmos, elevando a 2:
t(n) = 2(3+log 3)n – log n – 2 = 23n·2log 3·n·2-log n·2-2 =
= (23n-2·3n)/n = 24n/4n
Quitar la condición de que n sea potencia de 2.
¿Cuánto vale O(t)?

3.4. Otras técnicas.
Expansión de recurrencias
Aplicar varias veces la fórmula recurrente hasta encontrar alguna “regularidad”.
Ejemplo. Calcular el número de mover, para el problema de las torres de Hanoi.
t(0) = 1
t(n) = 2 t(n-1) + 1.

Expansión de la ecuación recurrente:
t(n) = 2 t(n-1) + 1 = 22 t(n-2) + 2 + 1 = 23 t(n-3)+4+2+1=
n-1 n
= …… n ….. = 2n t(n-n) + ? 2i = ? 2i = 2n+1 – 1
i = 0 i = 0

3.4. Otras técnicas.
Expansión de recurrencias
Puede ser adecuada cuando sólo hay un término recurrente o cuando la ecuación es no lineal.

Ejemplo.
t(0) = 1
t(n) = n t(n-1) + 1

No aplicar si aparecen varios términos recurrentes:
t(n) = 5 t(n-1) – 8 t(n-2) + 4n – 3
t(1) = 3, t(2) = 10

3.4. Otras técnicas.
Inducción constructiva
Se usa cuando las ecuaciones son no lineales y no se puede aplicar ninguna de las técnicas anteriores.

Inducción: Dado t(n), suponer que pertenece a algún orden O(f(n)) y demostrarlo por inducción.
Caso base. Para algún valor pequeño, t(n) ? c1·f(n)
Caso general. Suponiendo que t(n-1) ? c1·f(n-1), entonces se demuestra que t(n) ? c1·f(n)

3.4. Otras técnicas.
Inducción constructiva

Ejemplo. Dada la siguiente ecuación recurrente, demostrar que t(n) ? ?(n!):
t(1) = a
t(n) = b·n2 + n·t(n – 1)

Demostrar por inducción que t(n) ? ?(n!).
Demostrar por inducción que t(n) ? O(n!).

3.5. Condiciones iniciales.
¿Cuál es el significado de las condiciones iniciales?
Condición inicial: caso base de una ecuación recurrente.
¿Cuántas aplicar?
Tantas como constantes indeterminadas.
n incógnitas, n ecuaciones: sistema determinado. Aplicamos el método de Cramer.
¿Cuáles aplicar?
Las condiciones aplicadas se deben poder alcanzar desde el caso general.
Si se ha aplicado un cambio de variable, deben cumplir las condiciones del cambio.

3.5. Condiciones iniciales.
Ejemplo.
t(n) = n Si n ? 10
t(n) = 5·t(n-1) – 8·t(n-2) + 4·t(n-3) Si n > 10

Resultado: t(n) = c1 + c22n + c3n·2n

Aplicar las condiciones iniciales para despejar c1, c2, c3.
¿Cuántas aplicar? ¿Cuáles?

3.5. Condiciones iniciales.
El cálculo de constantes también se puede aplicar en el estudio experimental de algoritmos.

Proceso
Hacer una estimación teórica del tiempo de ejecución.
Expresar el tiempo en función de constantes indefinidas.
Tomar medidas del tiempo de ejecución para distintos tamaños de entrada.
Resolver las constantes.

3.5. Condiciones iniciales.
N
R+
Ejemplo: t(n) = a(n+1)2 + (b+c)n + d
Simplificamos constantes: t(n) = c1n2 + c2n + c3
c1n2 + c2n + c3

3.5. Condiciones iniciales.
N
R+
Ajuste sencillo: Tomar 3 medidas de tiempo.3 incógnitas y 3 ecuaciones: resolvemos c1,c2,c3.
Tamaños grandes, y medidas separadas.
c1n2 + c2n + c3

3.5. Condiciones iniciales.
N
R+
Ajuste preciso: Tomar muchas medidas de tiempo.
Hacer un ajuste de regresión.
c1n2 + c2n + c3

4. Ejemplos.
Ejemplo 1. Dada la siguiente ecuación de recurrencia, con a, b, c y d ? R+ y e, n0 ? N+:

f(n) =

Demostrar que: a < 1 ? f ? O(n)
a = 1 ? f ? O(n2)
a > 1 ? f ? O(an/e)
d Si n ? n0

a·f(n-e) + bn + c Si n > n0

4. Ejemplos.
Ejemplo 2. Dada la siguiente ecuación de recurrencia, con a, b, c y p ? R+ y d, n0 ? N+:

f(n) =

Demostrar que: a < dp ? f ? O(np)
a = dp ? f ? O(np·log n)
a > dp ? f ? O(nlogd a)
c Si n ? n0

a·f(n/d) + bnp Si n > n0

4. Ejemplos.
Ejemplo 3. Calcular el número de instrucciones de asignación del siguiente algoritmo.

procedure Otro (n: integer): integer;
for i:= 1 to n do
M[i]:= M[i] + 1
if i>0 then
Otro(n-4)

4. Ejemplos.
Ejemplo 4. El tiempo de ejecución de determinado programa se puede expresar con la siguiente ecuación de recurrencia:

t(n) =

Calcula el tiempo de ejecución para los valores de n que sean potencia de 2. Exprésalo con las notaciones O, ? ó ?.
Muestra las condiciones iniciales que se deberían aplicar.
Eliminar la condición de que n sea potencia de 2.
La afirmación t(n) ? ?(log n) ¿es correcta en este caso?, ¿es una buena cota para el orden de complejidad del programa?
2n Si n ? 10

2t(?n/2?) + 3t(?n/4?) + 2n + 1 En otro caso

Conclusiones:
Eficiencia: consumo de recursos en función de los resultados obtenidos.
Recursos consumidos por un algoritmo: fundamentalmente tiempo de ejecución y memoria.
La estimación del tiempo, t(n), es aproximada, parametrizada según el tamaño y el caso (tm, tM, tp).
Conteo de instrucciones: obtenemos como resultado la función t(n)
Para simplificar se usan las notaciones asintóticas: O(t), ?(t), ?(t), o(t).

1. Análisis de algoritmos.
Conclusiones:
Ecuaciones recurrentes: surgen normalmente del conteo (de tiempo o memoria) de algoritmos recursivos.
Tipos de ecuaciones recurrentes:
Lineales, homogéneas o no homogéneas.
No lineales (menos comunes en el análisis de algoritmos).
Resolución de ecuaciones recurrentes:
Método de expansión de recurrencias (el más sencillo).
Método de la ecuación característica (lineales).
Cambio de variable (previo a la ec. característica) o transformación de la imagen.
Inducción constructiva (general pero difícil de aplicar).