
1
Matemáticas Avanzadas para Ingeniería
Fue en Grenoble ( Sur de Francia ) donde Jean-Baptiste Joseph Fourier (1768–1830) condujo sus experimentos sobre la propagación del calor que le permiten modelar la evolución de la temperatura a través de series trigonométricas.
Estos trabajos provocan un adelanto en el proceso de modelación matemática en fenómenos físicos y contribuyeron a los fundamentos de la termodinámica.
Sin embargo, la simplificación excesiva que proponen estas herramientas fue muy debatida, principalmente por Pierre-Simon Laplace y Joseph-Louis Lagrange.

2
Fourier, seguidor de la teoría matemática de la conducción del calor, estableció la ecuación diferencial parcial que gobierna la difusión del calor solucionándolo por el uso de series infinitas de funciones trigonométricas. En esto introduce la representación de una función como una serie de senos y cosenos, ahora conocidas como las series de Fourier.
El trabajo de Fourier provee el ímpetu para más tarde trabajar en series trigonométricas y la teoría de las funciones de variables reales.
En la obra Théorie analytique de la chaleur (Teoría Analítica del calor) (1822) de Fourier, los dos primeros capítulos tratan problemas sobre difusión de calor entre cuerpos disjuntos en cantidad finita, es decir el problema discreto.
Matemáticas Avanzadas para Ingeniería

3
En el capítulo III Difusión del calor en un cuerpo rectangular infinito es donde Fourier introduce su método original de trabajo con series trigonométricas.
Otro trabajo importante de J. Baptiste J. Fourier fue en el método de eliminación para la solución de un sistema de desigualdades, teoría muy usada actualmente para programación lineal.
Matemáticas Avanzadas para Ingeniería

4
Conceptos Principales En 1807, Fourier, establece en los trabajos presentados en el instituto de Francia que: cualquier señal periódica puede ser representada por una serie de sumas trigonométricas en senos y cosenos relacionadas armónicamente.
Los argumentos establecidos por Fourier eran imprecisos y en 1829 Dirichlet proporcionó las condiciones precisas para que una señal periódica pueda ser representada por una serie de Fourier.
Fourier obtuvo además, una representación para señales no periódicas, no como suma de senoides relacionadas armónicamente, sino como integrales de senoides, las cuales no todas están relacionadas armónicamente.
Al igual que las series de Fourier, la integral de Fourier, llamada Transformada de Fourier, es una de las herramientas más poderosas para el análisis de sistemas LTI (Sistema Lineal Invariante en el Tiempo).
Matemáticas Avanzadas para Ingeniería
5
Matemáticas Avanzadas para Ingeniería
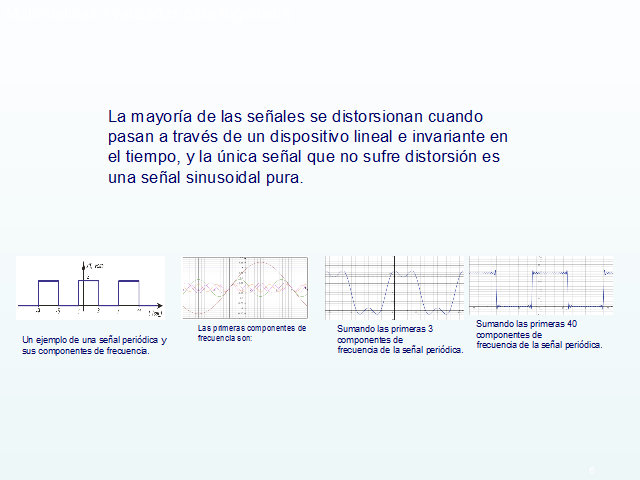
La mayoría de las señales se distorsionan cuando pasan a través de un dispositivo lineal e invariante en el tiempo, y la única señal que no sufre distorsión es una señal sinusoidal pura.
Sumando las primeras 40 componentes de
frecuencia de la señal periódica.
Las primeras componentes de frecuencia son:
Sumando las primeras 3 componentes de
frecuencia de la señal periódica.
Un ejemplo de una señal periódica y sus componentes de frecuencia.

6
Matemáticas Avanzadas para Ingeniería
Aplicaciones
Contenido: Señales y sistemas .
Señal
Sistema
Respuesta
Señal= función real del tiempo
Señal eléctrica: forma de onda de voltaje o corriente
Resistencia estándar, para todos los cálculos de energía y potencia se asume una resistencia de 1 ohm.

7
Matemáticas Avanzadas para Ingeniería
Justificación: :Señales y sistemas .
Análisis de Fourier descompone una señal en una suma de señales senoidales y analiza como se distribuye la energía y la potencia en cada una de esas frecuencias
Las señales se clasifican en:
Señales de Energía y
Señales de Potencia
Las Señales de Energía es una señal en forma de pulso que existe sólo en un intervalo finito de tiempo, o en la que al menos tiene la mayor parte de la energía concentrada en un intervalo finito de tiempo

8
Matemáticas Avanzadas para Ingeniería
Señales y sistemas .
Energía disipada por la señal en el intervalo de tiempo es:
Señal de energía se define como la señal que tiene energía finita aún cuando el intervalo de tiempo es infinito esto es cuando

9
Matemáticas Avanzadas para Ingeniería
Señales y sistemas .
Las primeras componentes de frecuencia son:
Sumando las primeras 3 componentes de
frecuencia de la señal periódica.
Un ejemplo de una señal periódica y sus componentes de frecuencia.
Ejemplos:
Señales de pulso Rectangular
Señales de pulso Senoidal
Señales de pulso Exponencial
Señales de pulso Gaussiano

10
Matemáticas Avanzadas para Ingeniería
Señales y sistemas .
Potencia promedio disipada por la señal

11
Matemáticas Avanzadas para Ingeniería
Señales y sistemas .
Señal de Potencia, se define como la señal que tiene potencia promedio finita, pero diferente de cero, aún cuando el intervalo de tiempo es infinito esto es cuando:

12
Cuando se aplica a un sistema lineal invariante en el tiempo, una señal sinusoidal no cambia su forma
pero sí cambian:
– Su amplitud.
– Su fase.
• En general, el cambio en la amplitud y en la
fase dependen:
– del sistema.
– de la frecuencia de la señal sinusoidal.
Matemáticas Avanzadas para Ingeniería
Página siguiente  |