
Movimiento
ondulatorio
Ondas
Velocidad de las ondas mecánicas
Ondas sonoras
Velocidad de las ondas sonoras
Características de las ondas armónicas
Contaminación acústica
Cualidades del sonido
MOVIMIENTO ONDULATORIO
Ondas mecánicas
Ondas armónicas
Mecanismo de formación
de las ondas sonoras
Función de onda
Energía de una onda armónica


1. Ondas
Más de una vez hemos visto las ondas producidas en la superficie del agua de un estanque al dejar caer sobre ella un objeto,o las formadas en una cuerda cuando la sacudimos. Igualmente conocemos las ondas sísmicas de tan catastróficos efectos y oímos el toque de las campanas de una iglesia cercana (ondas sonoras) .
¿Qué tienen en común todas estas ondas? ¿Qué las caracteriza?
Imaginemos la superficie del agua de un estanque.
Dejamos caer una piedra .
Vamos a fijarnos en algunas de las partículas del agua .
?No se realiza un transporte neto de las partículas del agua (lo que bajan,lo suben)
?Hay una transmisión de la energía que la piedra comunicó a la primera partícula y de esta al resto de las partículas, que oscilan como lo hizo la primera.
Un movimiento ondulatorio es una forma de transmisión de energía, sin transporte neto de materia, mediante la propagación de una perturbación.
A esta perturbación que se propaga a través de las partículas del medio se la denomina onda.
?Existe un cierto retraso entre el instante en que se produce la llegada de la piedra al agua y el instante en que la perturbación producida llega a las partículas más alejadas.

1. Ondas (Cont.)
Las ondas de radio, la luz, las ondas de televisión, el sonido, las ondas en una cuerda de guitarra, las ondas en la corteza de la Tierra (ondas sísmicas), las microondas, los rayos infrarrojos, … son ejemplos de movimientos ondulatorios.
Todos los fenómenos anteriores, de muy diverso origen, son tratados por la Física como fenómenos de naturaleza ondulatoria.
Podemos establecer una primera clasificación de las ondas:
Ondas mecánicas
Ondas electromagnéticas
Propagación de una perturbación de tipo mecánico a través de un medio material elástico por el que se transmite la energía mecánica. El medio material, que puede ser aire, agua, una cuerda, …. , es indispensable para que exista la onda.
Transmisión de energía electromagnética mediante la propagación de dos campos oscilatorios, el eléctrico y el magnético, que no requiere medio físico ya que son variaciones periódicas del estado eléctrico y magnético del espacio, que también se propagan en el vacío
El sonido es una onda mecánica, que requiere la presencia del aire para propagarse.
La luz es una onda electromagnética.
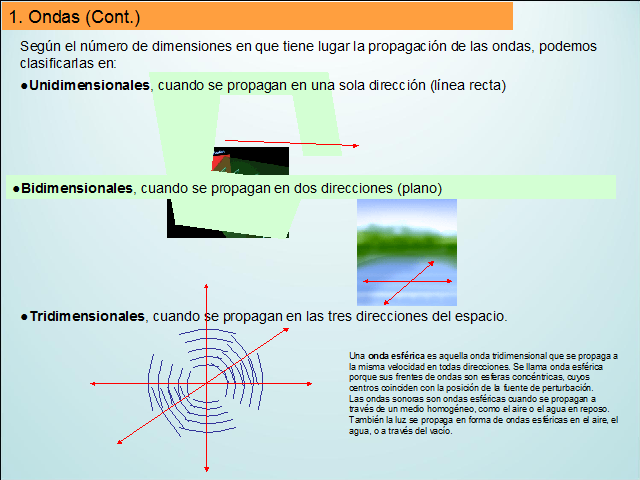
1. Ondas (Cont.)
Según el número de dimensiones en que tiene lugar la propagación de las ondas, podemos clasificarlas en:
?Tridimensionales, cuando se propagan en las tres direcciones del espacio.
?Unidimensionales, cuando se propagan en una sola dirección (línea recta)
?Bidimensionales, cuando se propagan en dos direcciones (plano)
Una onda esférica es aquella onda tridimensional que se propaga a la misma velocidad en todas direcciones. Se llama onda esférica porque sus frentes de ondas son esferas concéntricas, cuyos centros coinciden con la posición de la fuente de perturbación.
Las ondas sonoras son ondas esféricas cuando se propagan a través de un medio homogéneo, como el aire o el agua en reposo. También la luz se propaga en forma de ondas esféricas en el aire, el agua, o a través del vacío.

2. Ondas mecánicas
En esta unidad dedicaremos nuestra atención a las ondas mecánicas, aunque muchos de los conceptos y propiedades de éstas son aplicables a las ondas electromagnéticas. Estas las veremos en la unidad 10, La luz
Podemos clasificar las ondas mecánicas teniendo en cuenta la dirección de propagación de la onda en relación con el movimiento de las partículas del medio.
Ondas transversales
Ondas longitudinales
Una onda es transversal si su dirección de propagación es perpendicular a la dirección de la oscilación que provoca en las partículas del medio
Una onda es longitudinal si su dirección de propagación es paralela a la dirección de la oscilación que provoca en las partículas del medio
APPLET Educaplus
Ondas transversales Proyecto Newton
Ondas longitudinales Proyecto Newton
La luz es una onda transversal
El sonido es una onda longitudinal
Ondas CNICE

2.1. Velocidad de las ondas mecánicas
La velocidad de propagación de una onda es el cociente de dividir la distancia que avanza la onda entre el tiempo que emplea para ello.
Es la rapidez con que se desplaza la onda.
La velocidad de propagación de una onda mecánica depende de las propiedades del medio.
La velocidad de propagación v de las ondas transversales en una cuerda depende de la tensíon T de ésta y de su densidad lineal µ (masa m por unidad de longitud L)
Las ondas transversales mecánicas sólo pueden propagarse a través de medios sólidos, donde la rigidez de éstos permite el desarrollo de fuerzas recuperadoras o en la superficie de los líquidos.
La velocidad de propagación de la sondas longitudinales en sólidos depende de la constante elástica del medio y de su densidad, ya que las ondas longitudinales provocan contracciones y dilataciones en las partículas del sólido.

2.1. Velocidad de las ondas mecánicas (Cont.)
En un medio sólido, la velocidad de propagación de las ondas longitudinales es mayor que la de las ondas transversales.
La velocidad de propagación de la sondas longitudinales en los fluidos (líquidos y gases) depende del módulo de compresibilidad y de la densidad del medio.
La velocidad de propagación de las ondas sonoras es independiente de la fuente sonora que lo produce; sólo depende de las características del medio de propagación:
E = módulo de Young
d = densidad del sólido
Q = módulo de compresibilidad
d = densidad del líquido
del líquido
del sólido
P = presión del gas
? = Coeficiente adiabático del gas
d = densidad del gas
T = temperatura absoluta del gas
R = Constante de los gases
En los sólidos
En los líquidos
En los gases
M = Masa molar del gas

2.2. Energía del Oscilador armónico simple
Hemos visto que un oscilador armónico es un sistema material que se mueve con movimiento armónico simple MAS.
La energía mecánica que posee es CINÉTICA, porque está en movimiento y POTENCIAL ELÁSTICA, ya que el movimiento armónico es consecuencia de la acción de una fuerza conservativa (la fuerza elástica recuperadora).
Energía cinética
La partícula de masa m que se mueve con una velocidad v tendrá una energía cinética:
Energía potencial elástica
Para un oscilador cuya constante elástica es k, la energía potencial elástica en el instante que su elongación es x vale:
Energía mecánica
Es la suma de las dos anteriores:

Actividad 1
Calcular la velocidad de propagación de un pulso de onda en una cuerda de 3,00 m de longitud y 135 g de masa, si de ella cuelga un cuerpo de 4,00 kg (ver figura)
La fuerza que el cuerpo ejerce sobre la cuerda es igual y opuesta a la que la cuerda ejerce sobre el bloque (tensión). Y esta tiene el mismo valor que el peso del cuerpo.
Datos: L = 3,00 m ; m = 135 g ; mC = 4,00 kg ; g=9,8 m/s2
mC
La velocidad de una onda transversal ( o de un pulso) en una cuerda nos viene dada por la expresión:
T= tensión que soporta la cuerda
µ= densidad lineal de la cuerda
La densidad lineal de la cuerda es el cociente entre su masa y su longitud:
m = 0,135 kg
Ya podemos calcular la velocidad de propagación del pulso en la cuerda:

3. Ondas armónicas
De entre todos los movimientos ondulatorios, nos interesan en especial, los movimientos ondulatorios armónicos, que se caracterizan porque las partículas del medio vibran con un MAS
Llamamos ondas armónicas a las que tienen su origen en las perturbaciones periódicas producidas en un medio elástico por un movimiento armónico simple
3.1. Características de las ondas armónicas
Amplitud A es valor máximo de la elongación. En el S.I. se mide en m
Periodo T es el tiempo que emplea el movimiento ondulatorio en avanzar una longitud de onda o bien el tiempo que emplea un punto del medio en realizar una oscilación completa. En el S.I. se mide en s
Frecuencia f es el número de ondas que pasan por un punto del medio en la unidad de tiempo. En el S.I. se mide en Hertzios (Hz) o s –1.
Es la inversa del periodo:
Longitud de onda ? es la distancia mínima entre dos puntos consecutivos que se hallan en el mismo estado de vibración. En el S.I. se mide en m
De lo anterior deducimos que la velocidad de propagación v es:
Ondas CNICE

3.2. Función de onda
y (m)
x(m)
0
(Gp:) +A
(Gp:) – A
Foco
Propagación de la onda a la velocidad v
Supongamos una onda armónica unidimensional que se propaga a lo largo del eje x con una velocidad v
El foco es el punto o centro emisor de la onda. En él se produce la perturbación que se va a propagar a los otros puntos del medio
Como se trata de una onda armónica, el estado de vibración del foco nos viene dado por la ecuación del MAS:
P
x
El punto P, alejado una distancia x del foco, también ejecutará un MAS pero con cierto retraso t’:
Si suponemos nula la fase inicial
El estado de vibración (la elongación) del punto P en el instante t será el mismo que tenía el foco en el instante t – t’:
Teniendo en cuenta el valor de t’:
Página siguiente  |