
Ejemplo 2: Regresión lineal
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)

Potencia y velocidad son dos variables correlacionadas según un modelo lineal, cuya ecuación es:
El ajuste es excelente.
La correlación es positiva, ya que la pendiente también lo es.
Por cada CV de potencia, la velocidad máxima se incrementa en 0’75 Km/h
Es posible predecir qué velocidad se podría alcanzar a partir de una potencia determinada o bien a la inversa, determinar qué potencia se necesita para alcanzar una velocidad.
Estas predicciones se pueden realizar sin restricciones dentro del rango analizado (Interpolación). En cambio, fuera del rango sólo son posibles si no nos alejamos excesivamente de él (Extrapolación)
Correlación Potencia – Velocidad
1.5D SX Furio
1.1i SX
1,4i SX
1.6i VTS
1.6i 16V VTS
Conclusiones:
V = 0’75 P + 117 R2 = 0’9915
Ejemplo 3: Citroën Saxo
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)

Interpolación y Extrapolación
Ecuación:
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)

Ejemplo 4: Relación Profesores/Alumnosen las Universidades Españolas
Trazar la gráfica de la distribución
Calcular parámetros de la distribución
¿ Cuál es la Universidad con mejor proporción profesor/alumno?
¿Qué Universidad tiene la peor ratio y cuántos profesores necesitaría para equilibrarla?
Calcular los valores teóricos de profesores de la Universidad de Granada si ésta tenía 55123 alumnos en el curso 1994-95.
Calcular los valores de la FBD si ésta tenía 1100 alumnos
R2=0.998 b=0.0515 a=-17
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)

Ejemplo 4: Gráfica de distribuciónRelación Profesores/Alumnos en Universidades
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)

Modelos No Lineales
(Gp:) Log y
(Gp:) Log x
(Gp:) Ln y
(Gp:) x
(Gp:) y
(Gp:) Log x
Antes de proceder a la regresión, hay que transformar la ecuación no lineal, y = f(x), en otra del tipo Y = A + BX, donde Y, X, A y B son funciones de y, x, a y b respectivamente.
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)

Ejemplo 5: El Péndulo de Galileo
Una de las principales aportaciones de Galileo Galilei (1564-1642), fue encontrar la relación entre el tiempo o periodo de oscilación de un péndulo y su longitud. Esto permitió construir por primera vez en la historia relojes de gran precisión basados en péndulos. Dicen que la idea de correlacionar estas variables se le ocurrió en la iglesia de su ciudad natal, Pisa, mientras, absorto, observaba cómo oscilaban las lámparas del techo…
Estos datos podrían corresponder a un hipotético experimento realizado por Galileo…
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)

Las deducciones de Galileo
Para encontrar el modelo que relaciona periodo de oscilación, T, con la longitud del péndulo, L, Galileo bien pudo hacer las siguientes deducciones…
No es lineal
No es exponencial
Tampoco es logarítmica
Es potencial
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)

Cálculos de la Regresión Potencial para el Péndulo de Galileo
Como vamos a ajustar a un modelo potencial, hacemos el cambio de variables: X = log x e Y = log y. Por lo demás se procede exactamente igual a una regresión lineal, ajustando a una expresión del tipo Y = A + BX. Por último, de B y A calculados se despejan b y a respectivamente.
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)

Ley del Péndulo
Generalizando…
El periodo de oscilación de un péndulo es proporcional a la raíz cuadrada de su longitud
Se deduce que…
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)
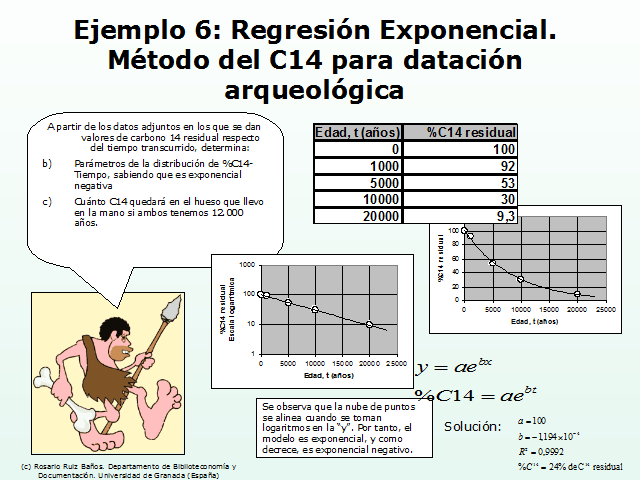
Ejemplo 6: Regresión Exponencial. Método del C14 para datación arqueológica
A partir de los datos adjuntos en los que se dan valores de carbono 14 residual respecto del tiempo transcurrido, determina:
Parámetros de la distribución de %C14-Tiempo, sabiendo que es exponencial negativa
Cuánto C14 quedará en el hueso que llevo en la mano si ambos tenemos 12.000 años.
Se observa que la nube de puntos se alinea cuando se toman logaritmos en la “y”. Por tanto, el modelo es exponencial, y como decrece, es exponencial negativo.
Solución:
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)

Cálculo de la Regresión Exponencial para el C14
Como se está ajustando un MODELO EXPONENCIAL hacemos el cambio de variable Y =LN(y), quedando x igual (X = x). En este caso A = Ln(a) y B = b.
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)

LOS MODELOS EN BIBLIOMETRÍA
La Bibliometría está fundamentada en un conjunto de “leyes empíricas”. Estas leyes se han establecido gracias a estudios cuantitativos en los que interviene el recuento de nº de artículos, nº de revistas, nº de autores, etcétera. Las distribuciones que correlacionan estas variables se ajustan mediante regresión lineal por el método de los mínimos cuadrados.
Las principales leyes y el tipo de modelo al que corresponden son las siguientes:
(c) Rosario Ruiz Baños. Departamento de Biblioteconomía y Documentación. Universidad de Granada (España)
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |