
Cómo describir la posición de un punto en el espacio: Sistemas de coordenadas
Un sistema de coordenadas que permita especificar posiciones consta de:
Un punto de referencia fijo, O, denominado origen
Un conjunto de direcciones o ejes especificados, con una escala y unas etiquetas apropiadas sobre sus ejes
Instrucciones que indican como etiquetar un punto en el espacio con respecto del origen y de los ejes.

Sistema de coordenadas cartesiano (u ortogonal)
Ejemplo en dos dimensiones:
Un punto arbitrario se define mediante las coordenadas (x,y)
y positivas hacia arriba
y negativas hacia abajo
x positivas hacia la derecha
x negativas hacia la izquierda

Sistema de coordenadas polar
Ejemplo en dos dimensiones:
Un punto arbitrario se define mediante las coordenadas polares planas (r,??)
? es el ángulo entre dicha línea y un eje fijo (normalmente el x)
r es la longitud de la línea que une el origen con el punto

Relación entre sistema de coordenas cartesianas y sistema de coordenadas polar
Ejemplo en dos dimensiones:
De polares a cartesianas
De cartesianas a polares,
asumiendo que ? está medida en sentido contrario de las agujas del reloj con respecto al eje x positivo

Dos tipos de magnitudes físicas importantes: escalares y vectoriales
Magnitud escalar:
aquella que queda completamente especificada mediante un número, con la unidad apropiada
Número de patatas en un saco
Temperatura en un determinado punto del espacio
Volumen de un objeto
Masa y densidad de un objeto
…
Magnitud vectorial:
aquella que debe ser especificada mediante su módulo, dirección y sentido
Posición de una partícula
Desplazamiento de un partícula (definido como la variación de la posición)
Fuerza aplicada sobre un objeto
…

Representación tipográfica de un vector
(Gp:) Letras en negrita: a
(Gp:) Flecha encima del símbolo:
(Gp:) Convenciones para representar una magnitud vectorial en un texto
(Gp:) Convenciones para representar el módulo de una magnitud vectorial en un texto
(Gp:) Letras en formato normal: a
(Gp:) Dos barras rodeando a la magnitud vectorial:
El módulo de un vector siempre es positivo, y especifica las unidades de la magnitud que el vector representa
(Cuántos metros me he desplazado)
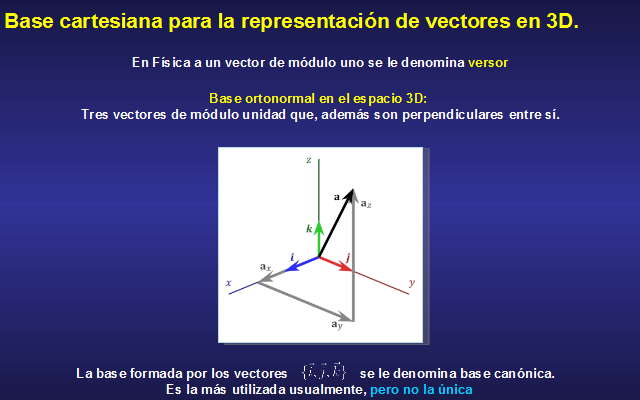
Base cartesiana para la representación de vectores en 3D.
En Física a un vector de módulo uno se le denomina versor
Base ortonormal en el espacio 3D:
Tres vectores de módulo unidad que, además son perpendiculares entre sí.
La base formada por los vectores se le denomina base canónica. Es la más utilizada usualmente, pero no la única

Componentes cartesianas de un vector
Proyecciones de un vector sobre los ejes de un sistema de coordenadas cartesiano
(Gp:) : componentes cartesianas de un vector
Página siguiente  |