
FORMAS DE EXPRESAR FUNCIONES BOOLEANAS
Forma POS (Suma de productos)
Suma (OR) de términos productos (AND), formadas por varias variables complementadas o no.
Forma POS (Producto de sumas)
Productos (AND) de términos sumas (OR) formados por varias variables complementadas o no.
f(a,b,c) = a’bc + ab’c’ + abc + c
Términos producto
f(a,b,c) = (a + b + c) (a + b’ + c) (c’ + a)
Términos suma
Formas de representación
FORMAS CANONICAS
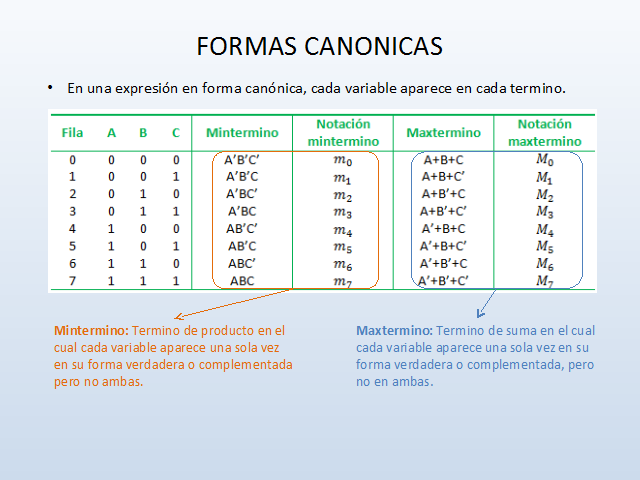
En una expresión en forma canónica, cada variable aparece en cada termino.
Mintermino: Termino de producto en el cual cada variable aparece una sola vez en su forma verdadera o complementada pero no ambas.
Maxtermino: Termino de suma en el cual cada variable aparece una sola vez en su forma verdadera o complementada, pero no en ambas.

FORMAS CANONICAS
F(A,B,C) = (A+B+C)(A+B’+C)(A’+B+C)
= M0.M2.M5
f(a,b,c) = A’B’C+A’BC+AB´C+ABC’+ABC
= m1 + m3 + m5 + m6 + m7
(Gp:) Por teorema de Demorgan es posible observar que:
(Gp:)
(Gp:) y
(Gp:)
m1’ = (A’B’C)’ = (A + B + C’) = M1

CONVERSION ENTRE FORMAS CANONICAS
Pasos:
Evaluar en que valores binarios se representa la SOP estándar
(Gp:) SOP estándar
(Gp:) POS estándar
f(x,y,z) = x’y’z’ + x’yz +
x’yz’ + xy’z
f(x,y,z)=(x+y+z’)(x’+y+z)
(x’+y’+z)(x’+y’+z’)
Determinar los números binarios no incluidos en el paso 1.
f(x,y,z) = x’y’z’ + x’yz + x’yz’ + xy’z
(Gp:) 000
(Gp:) 011
(Gp:) 101
(Gp:) 010
0
3
5
2
Escribir los términos suma equivalentes para los valores encontrados en el paso 2 y expresarlos en POS.
f(x,y,z) = (x + y + z’)(x’ + y + z)(x’ + y’ + z)(x’ + y’ + z’)

EJERCICIOS DE REPASO
Convierta a SOP estándar la siguiente función:
f(x,y,z,w) = xy + zw’ + x’w’
Convierta a POS estándar:
f(x,y,z,w) = (x + y’)(z + w’)(x + w)
Exprese la función en forma SOP y POS estándar:
f(x,y,z,w) = (x + y’ + w)(y’ + z + w’)(x + y’ + z’ + w)

SIMPLIFICACION DE CIRCUITOS LOGICOS
Algebra booleana:
Buen conocimiento de las reglas.
Habilidad para aplicar las reglas.
Mapas de Karnagh:
Método de simplificación grafico.
Basado en teoremas booleanos, pero de mayor facilidad al utilizarlo.
Mapas de Karnagh:
Método de simplificación tabular.
Directo, sistemático y no importa el numero de variables.
No lo vamos a tratar en el curso.

SIMPLIFICACION POR ALGEBRA BOOLEANA
Para la siguiente tabla de verdad encuentre las dos formas canónicas, la SOP, el POS y la forma no estándar mínima. Además represéntela en términos de su implementación en compuertas.
S = x’y’c + x’yc’ + xy’c’ + xyc
S = (x+y+c)(x+y’+c’)(x’+y+c’)(x’+y’+c)
Co = x’yc + xy’c + xyc’ + xyc
Co = (x’+y+c)(x+y’+c)(x+y+c’)(x+y+c)
(Gp:) POS canónica
(Gp:) POS canónica
(Gp:) SOP canónica
(Gp:) SOP canónica

SIMPLIFICACION POR ALGEBRA BOOLEANA
Para llevar la forma canónica a una forma no estándar simplificada se usa algebra booleana.
S = x’y’c + x’yc’ + xy’c’ + xyc
= c(x’y’+xy)+c’(x’y+xy’)
= (x?y)’c + (x?y)c’
= (x ? y) ? c
Co = x’yc + xy’c + xyc’ + xyc
= x’yc + xy’c + xyc’ + xyc + xyc
= x’yc + xy’c + xy(c’ + c) + xyc + xyc
= yc(x’+x) + xc(y’+y) + xy
= xy + yc +xc
Para su implementación en puertas lógicas se aprovecha uno de los XOR de la suma.
Co = x’yc + xy’c + xyc’ + xyc
= xy(c+c’)+c(x’y+xy’)
= xy + c(x ? y)

MAPAS DE KARNAUGH

MAPAS DE KARNAUGH
Los Mapas de Karnaugh se utilizan para hacer simplificación de funciones lógicas de 2, 3, 4, 5 y 6 variables como máximo.
Cada celda representa un mintermino.
(Gp:) 0
(Gp:) 0
(Gp:) 1
(Gp:) 1
(Gp:) 1
(Gp:) 4
(Gp:) 0
(Gp:) 5
(Gp:) 1
(Gp:) 3
(Gp:) 0
(Gp:) 2
(Gp:) 1
(Gp:) 7
(Gp:) 1
(Gp:) 6
(Gp:) A
(Gp:) BC
(Gp:) 00
(Gp:) 01
(Gp:) 10
(Gp:) 11
(Gp:) 0
(Gp:) 1

MAPAS DE KARNAUGH
Los mapas de Karnaugh utilizan código gray en la numeración de las celdas, esto hace que solo cambie una sola variable entre celdas adyacentes.
(Gp:) 0
(Gp:) 0
(Gp:) 1
(Gp:) 1
(Gp:) 1
(Gp:) 4
(Gp:) 0
(Gp:) 5
(Gp:) 1
(Gp:) 3
(Gp:) 0
(Gp:) 2
(Gp:) 1
(Gp:) 7
(Gp:) 1
(Gp:) 6
(Gp:) A
(Gp:) BC
(Gp:) 00
(Gp:) 01
(Gp:) 10
(Gp:) 11
(Gp:) 0
(Gp:) 1
(Gp:) 0
(Gp:) 1
(Gp:) 1
(Gp:) 3
(Gp:) 1
(Gp:) 0
(Gp:) 0
(Gp:) 2
(Gp:) 1
(Gp:) 7
(Gp:) 0
(Gp:) 5
(Gp:) 1
(Gp:) 6
(Gp:) 1
(Gp:) 4
(Gp:) C
(Gp:) AB
(Gp:) 00
(Gp:) 01
(Gp:) 10
(Gp:) 11
(Gp:) 0
(Gp:) 1
(Gp:) AB’C’
(Gp:) AB’C
(Gp:) A’B’C’
(Gp:) ABC’

SOP EN MAPAS DE KARNAUGH
Se dibuja el mapa y se coloca un 1 en las celdas que corresponden a los mintérminos de la función. Si se tiene una función SOP no estándar, ésta debe completarse y una vez hecho esto se ubican todos los mintérminos en el mapa de Karnaugh.
(Gp:) 0
(Gp:) 0
(Gp:) 1
(Gp:) 1
(Gp:) 1
(Gp:) 4
(Gp:) 1
(Gp:) 5
(Gp:) 1
(Gp:) 3
(Gp:) 0
(Gp:) 2
(Gp:) 0
(Gp:) 7
(Gp:) 0
(Gp:) 6
(Gp:) A
(Gp:) BC
(Gp:) 00
(Gp:) 01
(Gp:) 10
(Gp:) 11
(Gp:) 0
(Gp:) 1
(Gp:) 0
(Gp:) 1
(Gp:) 4
(Gp:) 5
(Gp:) 3
(Gp:) 2
(Gp:) 7
(Gp:) 6
(Gp:) A
(Gp:) BC
(Gp:) 00
(Gp:) 01
(Gp:) 10
(Gp:) 11
(Gp:) 0
(Gp:) 1
Página siguiente  |