
Ejemplo
Ejemplo 1 R = 20 W y L = 30mH, v(t) = 8 cos 103t.
R = 20;
L = 30e-3;
omega = 1000;
clf;hold off;
tiempo = linspace(0,8.1*1e-3,1000);
v = 8*cos(1e3*tiempo);
a = 8/sqrt(R^2+omega^2*L^2);
fase = atan(omega*L/R);
i = a*cos(1e3*tiempo – fase);
plot(tiempo,v,'-b',tiempo,i,':b');
xlabel('tiempo (sec.)');
ylabel('v (volts), i(amps)');
legend('v(t)','i(t)',0);

Ejemplo
Encontrar iL en la siguiente red
iL
Encontrar el equivalente de Thévenin entre a y b.
Circuito equivalente.

Tarea 6
Sea vs = 40 cos 8000t V en el circuito de la figura. Recurra al teorema Thévenin en los casos en que esté sea más adecuado, y determine el valor en t = 0 para: a) iL, b ) vL ,b) iR , c) i1. Donde vL es el voltaje en la bobina.
Respuesta: 18.71 mA, 15.97 V, 5.32 mA, 24.0 mA

Función forzada compleja
Una fuente senoidal esta descrita por
v(t) = Vm cos (wt + q)
La respuesta en alguna rama de la red eléctrica será de la forma
i(t) = Im cos (wt + f)
Una función forzada senoidal siempre da lugar a una respuesta forzada senoidal de la misma frecuencia en un circuito lineal.
Vm cos (wt + q)
Im cos (wt + f)

Función forzada compleja
Si cambiamos la fase de la fuente senoidal en 90º, la respuesta también cambiará su fase en 90º.
v(t) = Vm cos (wt +q – 90º) = Vm sen (wt + q)
respuesta
i(t) = Im cos (wt + f – 90º) = Im sen (wt + f)
Si aplicamos un voltaje imaginario jVm sen (wt + q) obtendremos jIm sen (wt + f)
jVm sen (wt + q)
jIm sen (wt + f)
Función forzada compleja
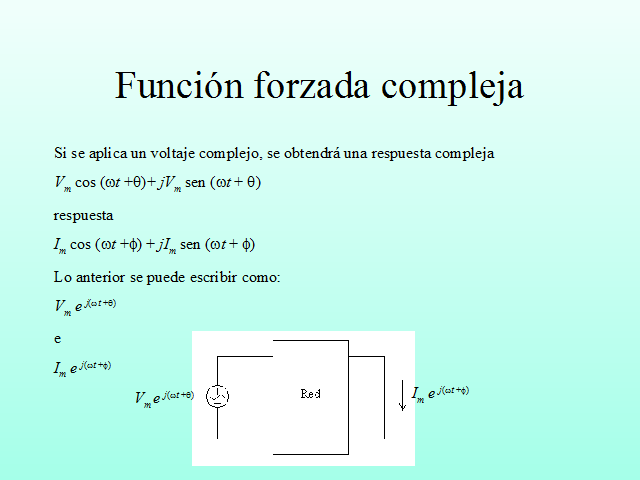
Si se aplica un voltaje complejo, se obtendrá una respuesta compleja
Vm cos (wt +q)+ jVm sen (wt + q)
respuesta
Im cos (wt +f) + jIm sen (wt + f)
Lo anterior se puede escribir como:
Vm e j(wt +q)
e
Im e j(wt +f)
Vm e j(wt +q)
Im e j(wt +f)

Función forzada compleja
Podemos resolver la ecuación del circuito RL utilizando estas funciones complejas.
sustituimos
v(t) = Vm e jwt
e
i(t) = Im e j(wt +f)
se obtiene

Función forzada compleja
Es fácil mostrar que
la corriente es la parte real de este número complejo.

Ejemplo
Determine la tensión compleja en la combinación en serie de un resistor de 50 Ohms y un inductor de 95mH si fluye la corriente compleja 8ej3000t.
Res.: 4.6ej(3000t + 29.7°) V

Tarea #7
Determine la tensión compleja que se produce cuando se aplica una corriente compleja 4ej800t A a la combinación serie de un capacitor de 1mF y un resistor de 2 Ohms.
Res.: 9.43ej(800t – 32°) V

Fasor
La corriente o la tensión a una frecuencia determinada se caracteriza por solo dos parámetros: amplitud y ángulo de fase.
La representación compleja de tensión o corriente contiene el factor ejwt, este puede eliminarse ya que no contiene información útil.
Representaremos la corriente o la tensión como números complejos en forma polar, a esta representación se le llama representación fasorial.

Representación fasorial
Proceso de transformación fasorial mediante el cual i(t) cambia a I.
i(t) = Im cos (wt + f)
?
i(t) = Re[Im e j(wt +f)]
?
I = Im e jf
?
I = Im?f
i(t) – representación en el domino del tiempo
I – representación en el domino de la frecuencia.
La representación fasorial es válida para alguna frecuencia w.

Ejemplos
v(t) = 100 cos(400t – 30°) V
Se suprime w = 400 rad/s y se obtiene el fasor
V = 100?–30°
–5 sen(580t – 110°) V
Se escribe como función coseno
–5 sen(580t – 110°) = 5 cos(580t – 110° + 90°)
= 5 cos(580t – 20°)
entonces
V = 5?–20°

Ejemplos
3 cos 600t –5 sen(600t + 110°)
= 3 cos 600t – 5(sen 600t cos 110°+ cos 600t sen 110°)
= 3 cos 600t – 5(– sen 600t sen 20° – cos 600t cos 20°)
= 3 cos 600t – 5(– 0.342sen 600t – 0.940cos 600t)
= 1.71cos 600t + 1.698sen 600t
= 2.41 cos(600t – 134.8°)
V = 2.41?–134.8°

Ejemplos
8 cos(4t + 30°)+ 4 sen(4t – 100°) =
8(cos 4t cos 30°– sen 4t sen 30°) + 4(sen 4t cos 100° – cos 4t sen 100°)
= 8(0.866 cos 4t – 0.5 sen 4t) + 4(–0.174 sen 4t – 0.985 cos 4t)
= 6.928 cos 4t – 4 sen 4t – 0.696sen 4t – 3.940 cos 4t
= 2.988 cos 4t – 4.696 sen 4t
= 5.566 cos(4t + 57.53°)
V = 5.566/_57.53°

Conversión al dominio del tiempo
El fasor con w = 500 rad/s
V = 2.41?–45°
Se transforma en
v(t) = 2.41 cos(500t – 45°) V = 2.41 sen(500t + 45°) V

Ejemplos
Sea w = 2000 rad/s y t = 1 ms. Encuentre la corriente instantánea para los siguientes fasores
a) j10 A.
j10 = 10?90° ? 10 cos(2000t + 90°) = 10 sen(2000t) en t = 1 ms se obtiene
10 sen(2 rad) = 9.09 A
b) 20 + j10 A
20 +j10 ? 22.6 ?26.6° ? 22.36 cos(2rad +26.6°)
= 22.36 cos(114.6°+ 26.6°)
= 22.36 cos(141.2°)
= – 17.43 A.
c) 20 + j(10?20°)A
20 + j(10?20°) = 20 + j(9.397 + j3.42)
= 16.58 + j9.397 ? 19.06 cos(114.6° + 29.54°)
= 19.06 cos(144.14°)
= – 15.44

Tarea #8
Exprese cada una de las siguientes corrientes como un fasor:
a) 12 sen(400t + 110°)A
b) –7sen 800t – 3cos 800t
Si w = 600 rad/s, determine el valor instantáneo de cada una de las siguientes tensiones en t = 5 ms,
a) 70?30° V
b) –60 + j40 V
Acos a + B sen a = ?A2+B2 cos(a+tan–1(-B/A))

Relación fasorial para R
Relación corriente voltaje para el resistor en el dominio del tiempo
v(t) = Ri(t)
Aplicando un voltaje complejo
Vm e j(wt +q) = RIm e j(wt +f)
Eliminando el término e jwt, encontramos
Vm e jq = RIm e jf
En forma polar
Vm?q = RIm?f
Por tanto:
V = RI

Relación fasorial para L
Aplicando un voltaje complejo
Vm e j(wt +q) = jwLIm e j(wt +f)
Eliminando el término e jwt, encontramos
Vm e jq = jwLIm e jf
En forma polar
Vm?q = jwLIm?f
Por tanto:
V = jwLI

Ejemplo
Aplique una tensión 8?–50° a una frecuencia w = 100 rad/s en un inductor de 4H y determine la corriente fasorial y la corriente en el dominio del tiempo.
De V = jwLI se tiene
I = V/jwL = 8?–50°/j100(4)
= – j0.02?–50°
= (1?–90°)(0.02?–50°)
= 0.02?–140°
i(t) = 0.02 cos(100t – 140°) A

Relación fasorial para C
Aplicando un corriente compleja
Im e j(wt +f) = jwCVm e j(wt +q)
Eliminando el término e jwt, encontramos
Im e jf = jwCVm e jq
En forma polar
Im?f = jwC Vm?q
Por tanto:
I = jwCV

Resumen de relaciones fasoriales

Leyes de Kirchoff con fasores
En el dominio del tiempo
v1 (t) + v2(t) + v3(t) +…+ vN(t) = 0
Sustituimos cada tensión real por una compleja y eliminamos el término e jwt, encontramos
V1 + V2 + V3 +…+ VN = 0

Circuito RL con fasores
VR + VL = Vs
Utilizando las relaciones fasoriales
RI + jwLI = Vs
Despejando I:
I = Vs/(R+ jwL)
Si tomamos V con ángulo de fase 0°,
I = Vm?0°/(R+ jwL)
En forma polar

Tarea #9
En la figura sea w = 1200 rad/s, IC = 1.2?28° A e IL = 3?53° A. Determine a) Is, b) Vs, c) iR(t)
2.33?-31° A , 34.9?74.5° V, 3.99cos(1200t + 17.42°)A.

10.7 Impedancia
Las relaciones de corriente-tensión para los tres elementos pasivos en el dominio de la frecuencia son (suponiendo que satisface la convención de signos pasiva):
Si las ecuaciones se escriben como proporciones tensión fasorial/corriente fasorial:

10.7 Impedancia
Definamos la proporción entre la tensión fasorial y la corriente fasorial como la impedancia, simbolizada por la letra Z. Es una cantidad compleja que tiene las dimensiones de ohms; no es un fasor y no puede transformarse al dominio del tiempo multiplicándola por ej?t y tomando la parte real.
ZR=R
ZL=j?L
ZC= 1
j?C

Resistencia y reactancia
A la parte real de la impedancia se le llama resistencia.
R = Re[Z]
La parte imaginaria de la impedancia se conoce como reactancia. Esta puede ser inductiva o capacitiva. Si es mayor que cero es inductiva, sino, es capacitiva.
X = Im[Z]
X > 0 — reactancia inductiva
X < 0 — reactancia capacitiva

Combinaciones de impedancia en serie
La impedancia del inductor es:
La impedancia del capacitor está dada por:
La impedancia de la combinación en serie corresponde por tanto a:

Combinaciones de impedancia en paralelo
La combinación en paralelo del inductor de 5mH y el capacitor de 100?F a ?=10000 rad/s se calcula del mismo modo que las resistencias en paralelo:
Con ?=5000? rad/s, el equivalente en paralelo es –j2.17
El número complejo o cantidad que representa a la impedancia se podría expresar en forma polar o en forma rectangular.

Ejemplo 10.5
Determine la impedancia equivalente de la red de la figura 10.17a, la cual produce una pulsación de operación de 5 rad/s.
a) Red que se va a sustituir por una sola impedancia equivalente. b) Los elementos se sustituyen por sus impedancias en ?= 5 rad/s.

Ejemplo 10.5
Empezamos conviertiendo los resistencias, capacitores y la bobina en impedancias. Luego de examinar la red resultante, observamos que la impedancia de 6? está en paralelo con –j0.4?. Esta convinación equivale a:

Ejemplo 10.5
La expresión anterior está en serie con las impedancias -j? y 10?, de modo que tenemos:
Esta nueva impedancia está en paralelo con 10?, por lo que la impedancia equivalente de la red resulta:
De manera alternativa, expresamos la impedancia en forma polar como 6.511?49.200

Práctica
10.9. De acuerdo con la red de la figura 10.18, determine la impeancia de entrada Zent que se mediría entre las terminales: a)a y g; b)b y g; c) a y b.
Respuestas: 2.81 + j4.49?; 1.798 – j1.24?; 0.1124 – j3.82?

Ejemplo 10.6
Determine la corriente i(t) en el circuito mostrado en la figura 10.19a.
a)Circuito RLC para el que se desea la respuesta forzada senoidal i(t). b)Equivalente en el dominio de la frecuencia del circuito dado en ?=300 rad/s

Técnicas de solución de problemas
Identifique el objetivo del problema.
Recopile la información conocida.
Decida la técnica la mejor técnica que mejor se ajusta al problema.
Construya un conjunto apropiado de ecuaciones.
Determine si se quiere información adicional.
Busque la solución.
Verifique la solución.¿Es razonable o la esperada?

Práctica ( tarea #10)
10.10. En el circuito de la figura 10.20, determine en el dominio de la frecuencia: a)I1; b)I2; c)I3
Respuestas: a) 28.3?450 A; b) 20?900 A; c)20?00A
Solución en Octave:
ZR = 5; ZC = -5j;ZL = 5j; V =100;
Z = ZC + ZL*ZR/(ZL+ZR);
I1 = V/Z
I2 = ZL/(ZL+ZR)*I1
I3 = ZR/(ZL+ZR)*I1

10.8 Admitancia
Definimos la admitancia Y de un elemento de circuito como la proporción entre la corriente fasorial y la tensión fasorial.
Y por ello
La parte real de la admitancia es la coductancia G, y la parte imaginaria de la admitancia es la es la susceptancia B, éstas se miden en siemens. De tal manera:

Análisis nodal y de mallas
Determine las tensiones de nodo v1(t) y v2(t).

Solución en Matlab
%Ejercicio 10-7
% determine las tensiones de nodo v1(t) y v2(t).
% +—C1—+
% +——+—-+—-+ +—–+—+—+
% ^ | | +—L1—+ | | |
% I1 R1 C2 L2 R2 I2
% | | | | | v
% +——+—-+——————-+—+—+
% Datos
C1 = -5j;
C2 = -10j;
R1 = 5;
R2 = 5;
L1 = 10j;
L2 = 5j;
I1 = 1;
I2 = -0.5j;
% Matriz de admitancias
Y = [1/R1+1/C2+1/C1+1/L1,-1/C1-1/L1;-1/C1-1/L1,1/R2+1/L2+1/C1+1/L1]
% vector de corrientes
I = [I1;I2]
% solucion
V = inv(Y)*I
% voltajes
polar(V(1))
polar(V(2))
fasor2t(V(1),10)
fasor2t(V(2),10)
% Solucion
% 3.69855 cos(10t + (-37.7468°))
% 1.37361 cos(10t + (-15.9454°))
function polar(z)
r = abs(z);
a = angle(z);
fprintf('%g/_%g°n',r,a*180/pi)
function fasor2t(v,w)
x = abs(v);
f = angle(v);
fprintf('%g cos(%gt + (%g°))n',x,w,f*180/pi)

Práctica ( tarea #11)
Escriba un guión en Octave para obtener vx(t) en el circuito de la figura si v1(t) = 20 cos1000t V y v2(t) = 20 sen1000t V. Utilice análisis de mallas. Ayuda: primero redibuje la red utilizando impedancias, luego plantee las ecuaciones con fasores e impedancias.
70.7cos(1000t – 45°) V

Ejemplo de superposición
-j 10 W
4 -j 2 W
2 +j 4 W
1?0°
0.5?-90°
V1
Encontrar V1 por superposición

Solución con Matlab
%Ejercicio 10-9
% determine las tensiones de nodo V1 por superposicion
% +——-+—Z1—+——+
% ^ | | |
% I1 Z2 Z3 I2
% | | | v
% +——-+——–+——+
% Datos
I1 = 1;
I2 = 0.5j;
Z1 = -10j;
Z2 = 4 – 2j;
Z3 = 2 + 4j;
% calculamos voltaje debido a I1, I2 = 0
% La impedancia equivalente es Z2 || (Z1+Z3)
Zeq = Z2*(Z1+Z3)/(Z2+Z1+Z3);
V1L = I1*Zeq
% calculamos voltaje debido a I2, I1 = 0
% encontramos la corriente que pasa por
% Z2 aplicando el divisor de
% corriente entre Z2+Z1 y Z3.
IZ2 = Z3/(Z1+Z2+Z3)*I2
V1R = IZ2*Z2
% el voltaje real es la suma de V1L y V1R
V1 = V1L + V1R
% Solucion
% V1 = 1.0000 – 2.0000i

Equivalente de Thévenin
-j 10 W
4 -j 2 W
2 +j 4 W
1?0°
0.5?-90°
V1
Encontrar el equivalente de Thévenin visto desde la impedancia de –j10 y con el encontrar V1.

Solución con Matlab
%Ejercicio 10-10
% Encontrar el equivalente de Thévenin visto
% desde la impedancia de -j10.
% V1
% +——-+—Z1—+——+
% ^ | | |
% I1 Z2 Z3 I2
% | | | v
% +——-+——–+——+
% Datos
I1 = 1;
I2 = 0.5j;
Z1 = -10j;
Z2 = 4 – 2j;
Z3 = 2 + 4j;
% calculamos el voltaje de circuito abierto
% visto desde La impedancia Z1
Voc = I1*Z2 – I2*Z3
% calculamos la impedancia equivalente
Zeq = Z2 + Z3
% podemos calcular la corriente I que
% circula en Z1
I = Voc/(Z1+Zeq)
% con esta corriente en el circuito original
% calculamos V1 restando de I1 el valor
% de I y multiplicando por Z2
V1 = (I1-I)*Z2
% Solucion
% V1 = 1.0000 – 2.0000i

Tarea #12
Determine la corriente i que pasa por el resistor de 4 W. Deberá utilizar la superposición ya que las fuentes son de distinta frecuencia.
i = 175.6 cos(2t – 20.55°) + 547.1 cos(5t – 43.16°) mA
i

Diagramas fasoriales
Un diagrama fasorial es un diagrama en el plano complejo que muestra las relaciones entre voltajes y corrientes fasoriales a través de un circuito específico.
V
53.1°
6
j8
Eje real (V)
Eje imaginario (V)

ejemplos
V1=3+j7
V2=3–j
V1 + V2
Suma de dos tensiones fasoriales.
V1
I1=(1+j1)V1
= ?2?45°
45°
Diagrama fasorial de I1 y V1 donde
I1 = YV1, y Y = 1 + j S = ?2?45° S

Ejemplo
VR = Vs
VL
VC
VR + VL
VR + VC
I
Circuito RLC serie
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |