Función de tensión senoidal
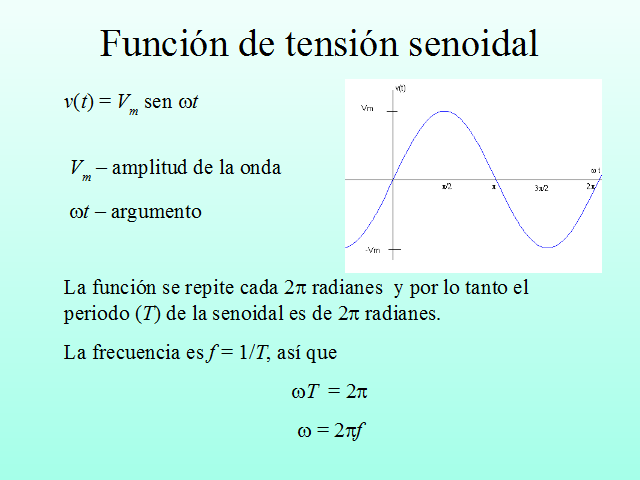
v(t) = Vm sen wt
Vm – amplitud de la onda
wt – argumento
La función se repite cada 2p radianes y por lo tanto el periodo (T) de la senoidal es de 2p radianes.
La frecuencia es f = 1/T, así que
wT = 2p
w = 2pf

Grafica de la función seno
Función senoidal en función de wt.
Código en Matlab
>> fplot('sin',[-pi/2 2*pi+0.1 -1.5 1.5])

Función senoidal en función de t.
Retraso y adelanto
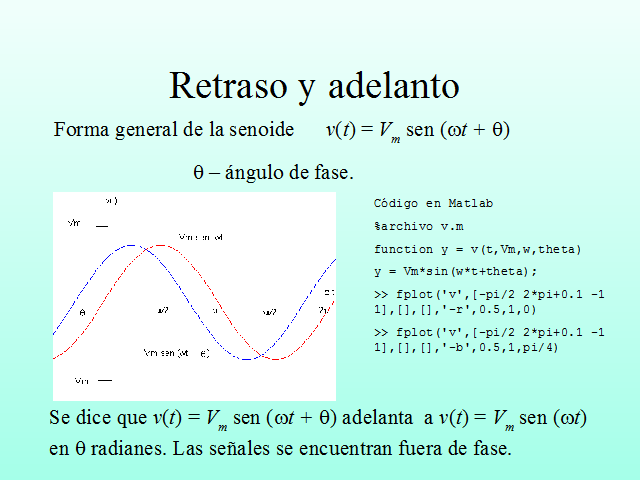
Forma general de la senoide
v(t) = Vm sen (wt + q)
q – ángulo de fase.
Código en Matlab
%archivo v.m
function y = v(t,Vm,w,theta)
y = Vm*sin(w*t+theta);
>> fplot('v',[-pi/2 2*pi+0.1 -1 1],[],[],'-r',0.5,1,0)
>> fplot('v',[-pi/2 2*pi+0.1 -1 1],[],[],'-b',0.5,1,pi/4)
Se dice que v(t) = Vm sen (wt + q) adelanta a v(t) = Vm sen (wt) en q radianes. Las señales se encuentran fuera de fase.

Conversión de senos a cosenos
Se cumple que
Vm sen wt = Vm cos(wt – 90°)
En general
– sen wt = sen(wt ? 180°)
– cos wt = cos(wt ? 180°)
sen wt = cos(wt ? 90°)
? cos wt = sen(wt ? 90°)

Ejemplo
Determinar el ángulo mediante el cual i1 está retrasada respecto a v1, si v1 = 120 cos(120pt – 40°) e i1 es igual a 1.4 sen(120pt – 70°)
1.4 sen(120pt – 70°) = 1.4 cos(120pt – 70° – 90°)
= 1.4 cos(120pt – 160°)
la diferencia de fases es
120pt – 40° – 120pt + 160° = 120°
por tanto el retraso es de 120°.

Tarea 5
Determinar el ángulo mediante el cual i1 está retrasada respecto a v1, si v1 = 120 cos(120pt – 40°) e i1 es igual a:
a) 2.5 cos(120pt + 20°)
b) –0.8 cos(120pt – 110°)
En general
– sen wt = sen(wt ? 180°)
– cos wt = cos(wt ? 180°)
sen wt = cos(wt ? 90°)
? cos wt = sen(wt ? 90°)

Respuesta forzada a funciones senoidales
Se utilizan los términos respuesta forzada o respuesta a estado permanente.
Considere el circuito serie RL con una fuente senoidal v(t) = Vm cos wt.
Aplicando LKV
VL + VR = v(t)
VL
VR
–
–
+
+

Respuesta forzada a funciones senoidales
Se debe cumplir con la ecuación diferencial
La corriente debe ser senoidal, en general puede ser de la forma:
i(t) = I1cos wt + I2 sen wt
Sustituyendo se obtiene
L(– I1wsen wt + I2wcos wt) +R(I1cos wt + I2sen wt) = Vmcos wt

Respuesta forzada a funciones senoidales
Agrupando términos con seno y con coseno, se obtiene
(–LI1 w + RI2)sen wt + (LI2w + R I1 –Vm) cos wt = 0
esto debe cumplirse para todo t, por lo tanto los coeficientes del seno y del coseno deben ser cero. Es decir:
–LI1 w + RI2 = 0 y LI2w + R I1 –Vm = 0
despejando I1 e I2 se obtiene
La respuesta forzada se escribe como:

Respuesta forzada a funciones senoidales
Suponiendo una respuesta de la forma
i(t) = A cos (wt – q)
Procedemos a determinar A y q, desarrollando el coseno de la resta de ángulos
de aquí encontramos que
dividiendo

Respuesta forzada a funciones senoidales
elevando al cuadrado las anteriores y sumando
En consecuencia
Página siguiente  |