
De la Serie de Fourier a la Transformada de Fourier
La serie de Fourier nos permite obtener una representación en el dominio de la frecuencia de funciones periódicas f(t).
¿Es posible extender de alguna manera las series de Fourier para obtener una representación en el dominio de la frecuencia de funciones no periódicas?
Consideremos la siguiente función periódica de periodo T:

Tren de pulsos de amplitud 1, ancho p y periodo T:
(Gp:) 1
(Gp:) f(t)
(Gp:) t
(Gp:) . . . -T -T/2 0 T/2 T . . .
(Gp:) p
(Gp:) -p/2 p/2

Los coeficientes de la serie compleja de Fourier en este caso resultan puramente reales:
El espectro de frecuencia correspondiente lo obtenemos (en este caso) graficando cn contra w = nw0.

Espectro del tren de pulsos para p = 1, T = 2

Si el periodo del tren de pulsos aumenta…
-20
-10
0
10
20
0
0.5
1
1.5
p = 1, T = 2
t
f(t)
t
-20
-10
0
10
20
0
0.5
1
1.5
p = 1, T = 5
f(t)
(Gp:) -20
(Gp:) -10
(Gp:) 0
(Gp:) 10
(Gp:) 20
(Gp:) 0
(Gp:) 0.5
(Gp:) 1
(Gp:) 1.5
(Gp:) p = 1, T = 10
(Gp:) t
(Gp:) f(t)
(Gp:) -20
(Gp:) -10
(Gp:) 0
(Gp:) 10
(Gp:) 20
(Gp:) 0
(Gp:) 0.5
(Gp:) 1
(Gp:) 1.5
(Gp:) p = 1, T = 20
(Gp:) t
(Gp:) f(t)

(Gp:) -50
(Gp:) 0
(Gp:) 50
(Gp:) -0.1
(Gp:) 0
(Gp:) 0.1
(Gp:) 0.2
(Gp:) 0.3
(Gp:) p = 1, T = 5
-50
0
50
(Gp:) -0.05
(Gp:) 0
(Gp:) 0.05
(Gp:) 0.1
(Gp:) 0.15
(Gp:) p = 1, T = 10
(Gp:) -50
(Gp:) 0
(Gp:) 50
(Gp:) -0.02
(Gp:) 0
(Gp:) 0.02
(Gp:) 0.04
(Gp:) 0.06
(Gp:) p = 1, T = 20
-50
0
50
(Gp:) -0.2
(Gp:) 0
(Gp:) 0.2
(Gp:) 0.4
(Gp:) 0.6
(Gp:) p = 1, T = 2
(Gp:) w=nw0
(Gp:) cn
…el espectro se "densifica".

En el límite cuando T??, la función deja de ser periódica:
¿Qué pasa con los coeficientes de la serie de Fourier?
(Gp:) -20
(Gp:) -10
(Gp:) 0
(Gp:) 10
(Gp:) 20
(Gp:) 0
(Gp:) 0.5
(Gp:) 1
(Gp:) 1.5
(Gp:) p = 1, T = ?
(Gp:) t
(Gp:) f(t)

Si hace T muy grande (T??), el espectro se vuelve "continuo":

El razonamiento anterior nos lleva a reconsiderar la expresión de una función f(t) no periódica en el dominio de la frecuencia, no como una suma de armónicos de frecuencia nw0, sino como una función continua de la frecuencia w.
Así, la serie:
al cambiar la "variable discreta" nw0 (cuando T??) por la variable continua w, se transforma en una integral de la siguiente manera:

Recordemos:
La serie de Fourier es:
-T/2< x < T/2
O bien:
Cuando T? ?, nw0 ? w y w0 ? dw y el sumatorio
se convierte en:

La transformada de Fourier
Es decir,
donde:
Estas expresiones nos permiten calcular la expresión F(w) (dominio de la frecuencia) a partir de f(t) (dominio del tiempo) y viceversa.
(Gp:) Identidad
de Fourier
o antitrans-
formada de
Fourier
(Gp:) Transformada
de Fourier

La transformada de Fourier y la transformada inversa de Fourier

Notación: A la función F(w) se le llama transformada de Fourier de f(t) y se denota por F o , es decir
En forma similar, a la expresión que nos permite obtener f(t) a partir de F(?) se le llama transformada inversa de Fourier y se denota por F –1 ,es decir

Transformadas integrales
K(?,t): núcleo o kernel.
Asocia a cada función f(t) en el espacio t, directo o real, otra función F(?) en el espacio ? o recíproco.
Ejemplos: de Fourier, Wavelet, transformada Z, de Laplace, de Hilbert, de Radon, etc

Un problema que es difícil de resolver en sus "coordenadas" (espacio t) originales, a menudo, es más sencillo de resolver al transformarlo a espacio ?.
Después, la transformada inversa nos devuelve la solución en el espacio original.
Problem in
Transform space
Original
problem
Solution in
Transform space
Solution of
original problem
Integral transform
Relatively easy solution
Difficult solution
Inverse transform

Ejemplo. Calcular F(?) para el pulso rectangular f(t) siguiente:
Solución. La expresión en el dominio del tiempo de la función es:
(Gp:) -p/2 0 p/2
(Gp:) 1
(Gp:) f(t)
(Gp:) t

Integrando:
Usando la fórmula
de Euler:

En forma gráfica,
la transformada es:
p =1

Sinc(x/2) es la transformada de Fourier de una función rectángulo.
Sinc2(x/2) es la transformada de Fourier de una función triangulo.
Sinc2(ax) es el patrón de difración de una ranura.
La función sinc(x)

Demostrar que la transformada de Fourier de la función triángulo, D(t), es sinc2(w/2)
w
0
1
t
0
1
1/2
-1/2
TF
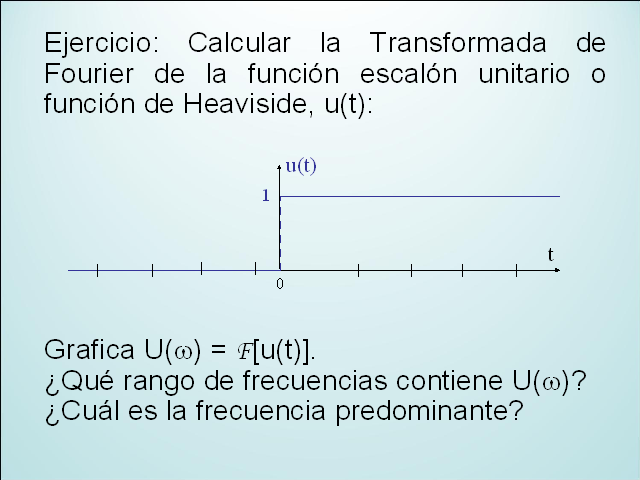
Ejercicio: Calcular la Transformada de Fourier de la función escalón unitario o función de Heaviside, u(t):
Grafica U(w) = F[u(t)].
¿Qué rango de frecuencias contiene U(w)?
¿Cuál es la frecuencia predominante?
(Gp:) u(t)
(Gp:) 0
(Gp:) 1
(Gp:) t
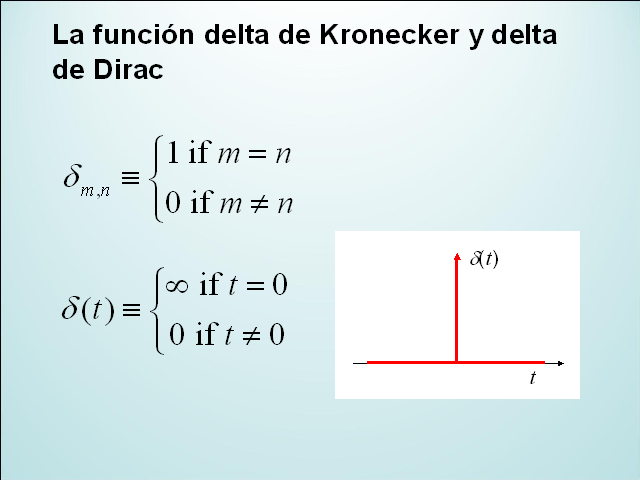
La función delta de Kronecker y delta de Dirac
(Gp:) t
(Gp:) d(t)

La función impulso o delta de Dirac
Podemos pensar en la función delta como el límite de una serie de funciones como la siguiente:
t
f1(t)
(Gp:) f2(t)
fm(t) = m exp[-(mt)2]/vp
(Gp:) f3(t)
(Gp:) d(t)

Propiedades de la función d
(Gp:) t
(Gp:) d(t)

Transformada de Fourier de la ?(t):
(Gp:) t
(Gp:) d(t)
w
w
d(w)
Observa que la transformada de Fourier de
f(t) = 1 es:
t
Recordemos


(Gp:) T 8
(Gp:) T 8
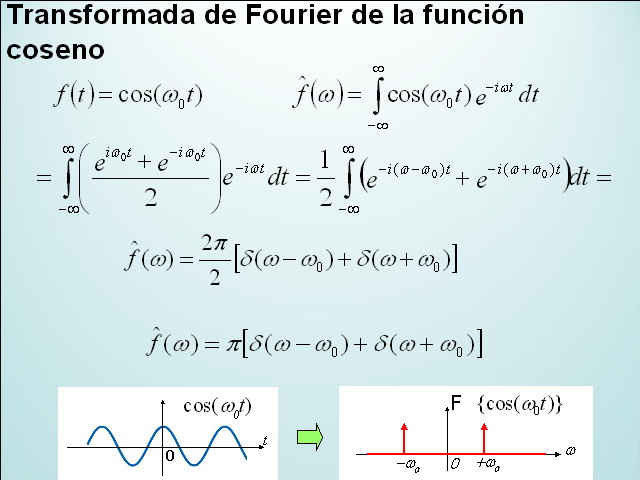
Transformada de Fourier de la función coseno
+w0
0
-w0
w
(Gp:) cos(w0t)
(Gp:) t
(Gp:) 0

Transformada de Fourier de la función seno:
+w0
0
-w0
w
sen(w0t)
t
0
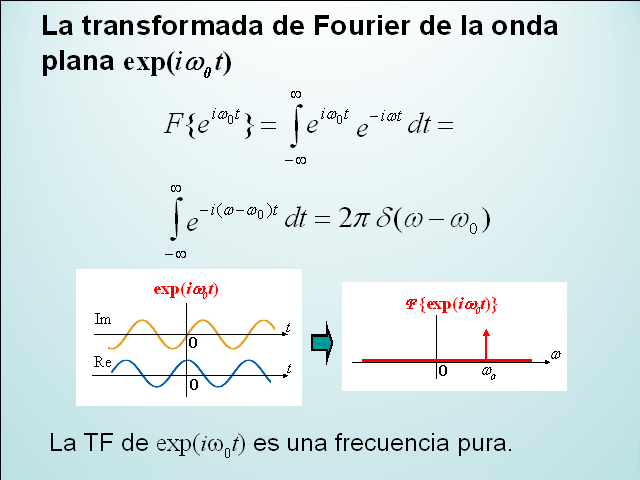
La transformada de Fourier de la onda plana exp(iw0 t)
La TF de exp(iw0t) es una frecuencia pura.
F {exp(iw0t)}
0
w0
w
(Gp:) exp(iw0t)
(Gp:) 0
(Gp:) t
(Gp:) t
(Gp:) Re
(Gp:) Im
(Gp:) 0

(Gp:) Sum
F {exp(iw0t)}
0
w0
w
(Gp:) exp(iw0t)
(Gp:) 0
(Gp:) t
(Gp:) t
(Gp:) Re
(Gp:) Im
(Gp:) 0
TF
0
w
TF

Encontrar la transformada de Fourier de la función:

La transformada de Fourier de una Gaussiana, exp(-at2), es ella misma.
(Gp:) t
(Gp:) 0
(Gp:) w
(Gp:) 0
TF

La transformada inversa de Fourier
Dada la función en el espacio recíproco G(k), podemos retornar al espacio directo mediante la inversa de la transformada de Fourier:

Algunas funciones no poseen transformada de Fourier
La condición de suficiencia para que la transformada de
Fourier de f(x), F(w) exista es:
es decir, que f(x) sea de cuadrado sumable. Funciones
que no vayan asintóticamente a cero cuando x tiende a
+¥ y –¥ en general no tienen transformadas de Fourier.

La TF y su inversa son simétricas.
Si la TF de f(t) es F(w), entonces la TF de F(t) es:
Renombrando la variable de integración de t a w’, podemos ver que llegamos a la TF inversa:
Este el motivo por el que a menudo f y F se dice que son
un "par transformado"
Que podemos escribir:

Fourier Transform Magnitude and Phase
Como en el caso de cualquier complejo, podemos descomponer f(t) y F(w) en su magnitud y fase. f(t) puede escribirse como:
f(t) = Mag{f(t)} exp[ -i Phase{f(t)}]
donde Mag{f(t)}2 es a menudo llamada intensidad,
I(t) y Phase{f(t)} es llamada fase, f(t).
Análogamente:
F(w) = Mag{F(w)} exp[ -i Phase{F(w)}]
Mag{F(w)}2 se llama espectro, S(w) y Phase{F(w)}
se llama el espectro de fase, j(w).

La transformada de Fourier es en general compleja
La transformada de Fourier F(k) y la función originial f(x) son ambas en general complejas.
De modo que la transformada de Fourier puede escribirse como:

La transformada de Fourier cuando f(x) es real
La TF F(k) es particularmente simple cuando f(x) es real:

ESTA PRESENTACIÓN CONTIENE MAS DIAPOSITIVAS DISPONIBLES EN LA VERSIÓN DE DESCARGA