
Contenido
Momento lineal y su conservación
Conservación de la cantidad de movimiento para dos partículas
Impulso y momento
Colisiones
Clasificación de las colisiones
Colisiones perfectamente inelásticas
Choques elásticos
Colisiones en dos dimensiones
Centro de masa
Centro de masa de un objeto extendido
Movimiento de un sistema de partículas

La cantidad de movimiento de una partícula se define como el producto de la velocidad v por la masa de la partícula:
p = mv
La segunda ley de Newton establece que la fuerza sobre un objeto es igual a la rapidez de cambio de la cantidad de movimiento del objeto.
En términos de la cantidad de movimiento, la segunda ley de Newton se escribe como:
Momento líneal y su conservación

Para dos partículas que interactúan se cumple que:
De la tercera ley de Newton, tenemos que:
Conservación de la cantidad de movimiento para dos partículas
m1
m2
F12
F21
P1 = m1v1
P2 = m2v2

De aquí se obtiene que:
Esto significa que: ptotal = p1 + p2 = constante
La ley de la conservación del momento lineal establece que siempre que dos partículas aisladas interactúan entre sí, su momento total permanece constante.

Impulso y momento
El impulso se define como el cambio en la cantidad de movimiento de un cuerpo:
El impulso de la fuerza F es igual al cambio de momento de la partícula.
El impulso es un vector que tiene una magnitud igual al área bajo la curva de fuerza-tiempo.
(Gp:) ti
(Gp:) tf
(Gp:) t
(Gp:) F

La fuerza F que actúa en un tiempo muy corto, y se le llama fuerza de impulso.
El impulso se puede escribir como: I = Fm Dt. Donde Fm es la fuerza promedio durante el intervalo.
ti
tf
t
F
Fm
Área = Fm Dt

Ejemplo
Una pelota de golf de 50 g es golpeada por un palo de golf y ésta alcanza una distancia de 200m, calcule el impulso aplicado por el palo, suponga un ángulo de 45° el la velocidad inicial.
El alcance esta dado por:
A
B
C
I = Dp = mvB – mvA = (0.050)(44) = 2.2 kg m/s
El alcance esta dado por:
Si el tiempo de contacto dura 4.5 x 10–4 s la fuerza es:
F = I/Dt = 4900 N

Colisiones
Llamamos colisión a la interacción de dos (o más) cuerpos mediante una fuerza impulsiva. Si m1 y m2 son las masas de los cuerpos, entonces la conservación de la cantidad de movimiento establece que:
m1v1i + m2v2i = m1v1f + m2v2f
Donde v1i, v2i, v1f y v2f son las velocidades iniciales y finales de las masas m1 y m2.
m1
m2
F12
F21
v1f
v1i
v2f
v2i
antes
después

Ejemplo
Un automóvil de 1800 kg está detenido y es golpeado por atrás por otro automóvil de 900 kg y los dos quedan enganchados. Si el auto pequeño se movía a 20 m/s ¿cuál es la velocidad final de los dos?
pi = m1v1i = (900)(20) = 18000 kg m/s
pf = m1vf + m2vf = (m1 + m2) vf = 2700 vf
vf = 18000/2700 = 6.67 m/s

Consideraremos colisiones en una dimensión.
Las colisiones se clasifican en:
Elásticas: cuando se conserva la energía cinética total, es decir:
Inelásticas: cuando parte de la energía cinética total se transforma en energía no recuperable (calor, deformación, sonido, etc.).
Perfectamente inelásticas: cuando los objetos permanecen juntos después de la colisión.
v1f = v2f
Clasificación de las colisiones

Para colisiones perfectamente inelásticas se cumple lo siguiente:
Si m2 está inicialmente en reposo, entonces:
Si m1» m2, entonces v ? v1i.
Si m1« m2, entonces v ? 0.
Si v2i = -v1i , entonces:
Si en este caso m1= m2, entonces: v = 0
Colisiones perfectamente inelásticas
m1
m2
v1i
v2i
m1+m2
vf
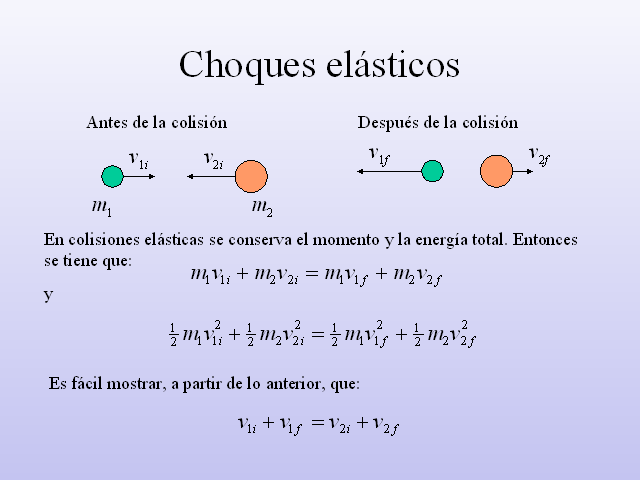
En colisiones elásticas se conserva el momento y la energía total. Entonces se tiene que:
y
Es fácil mostrar, a partir de lo anterior, que:
m1
m2
v1i
v2i
v2f
v1f
Antes de la colisión
Después de la colisión
Choques elásticos

Es fácil mostrar que las velocidades finales de los dos objetos son:
En una colisión elástica la velocidad relativa de los cuerpos en colisión cambia de signo, pero su magnitud permanece inalterada.
Si denotamos por u la velocidad relativa de los objetos, entonces:

Si m1 = m2, entonces v1f = 0 y v2f = v1i. Es decir, dos objetos de masas iguales intercambian sus velocidades.
Si m1 » m2, entonces v1f ? v1i y v2f ? 2v1i. Quiere decir que un objeto grande que choca con otro pequeño casi no altera su velocidad pero el objeto pequeño es arrojado con una velocidad del doble de la del pesado.
Si m1 « m2, entonces v1f ? -v1i y v2f ? (2 m1/m2)v1i ? 0. Cuando un objeto ligero choca con otro pesado, adquiere una velocidad opuesta a la que traía.
Si v2i = 0, entonces:

Colisiones en dos dimensiones
Para el caso de dos dimensiones la conservación del momento se expresa para cada componente como:
m1v1ix + m2v2ix = m1v1fx + m2v2fx
m1v1iy + m2v2iy = m1v1fy + m2v2fy
m1
m2
v1i
v2f
v1f
Antes de la colisión
Después de la colisión
v2i

Consideraremos el caso en que m2 está en reposo inicialmente. Después del choque m1 se mueve a un ángulo q con la horizontal y m2 se mueve a un ángulo f con la horizontal. Las ecuaciones anteriores quedan como:
m1v1i = m1v1fcos q + m2v2fcos f
0 = m1v1f sen q – m2v2fsen f
m1
m2
v1i
v2f
v1f
Antes de la colisión
Después de la colisión
f
q
La ley de la conservación de la energía suministra otra ecuación. Sin embargo, dadas las masas y la velocidad inicial deberá darse alguna de las cantidades restantes v1f,v2f, f, q.

Ejemplo
Un auto de 1500 kg a 25 m/s hacia el este choca con una camioneta de 2500 kg que se mueve hacia el norte a 20 m/s en un cruce. Encuentre la magnitud y dirección de la velocidad de los autos después del choque, suponga un choque perfectamente inelástico.
25 m/s
20 m/s
vf
Momento en x:
Antes Después
(1500 kg)(25 m/s) = (4000 kg) vf cos(q)
Momento en y:
Antes Después
(2500 kg)(20 m/s) = (4000 kg) vf sen(q)
Resolviendo
q = 53.1° vf = 15.6 m/s
q

Ejemplo
q
35°
v1i
v1f
v2f
y
x
En un juego de billar un jugador desea meter la bola objetivo en la buchaca de la esquina.
Conservación de la energía
Conservación del momento (bidimensional)
Efectuando el producto punto
q = 55°

Centro de masa
El centro de masa de un sistema de partículas es un punto en el cual paracería estar concentrada toda la masa del sistema.
En un sistema formado por partículas discretas el centro de masa se calcula mediante la siguiente fórmula:
(Gp:) m1
(Gp:) m2
(Gp:) mn
(Gp:) mi
(Gp:) r1
(Gp:) r2
(Gp:) ri
(Gp:) rn
(Gp:) rCM
(Gp:) x
(Gp:) y
(Gp:) z

Centro de masa de un objeto extendido
rCM
x
y
z
ri
Dmi
El centro de masa de un objeto extendido se calcula mediante la integral:
El centro de masa de cualquier objeto simétrico se ubica sobre el eje de simetría y sobre cualquier plano de simetría.

Movimiento de un sistema de partículas
Si se deriva respecto al tiempo el centro de masa de un sistema de partícula se obtiene la velocidad del centro de masa:
El momento total del sistema es:

La aceleración del centro de masa es:
De la segunada ley de Newton:
Tomando en cuenta la 3era. Ley de Newton:
El centro de masa se mueve como una partícula imaginaria de masa M bajo la influencia de la fuerza externa resultante sobre el sistema.