Generación de números y variables aleatorias

Hasta el minuto hemos descrito como los experimentos de simulación, seleccionan de una fuente de números aleatorios. Es importante por lo tanto disponer de un buen generador de números aleatorios en aéreas de la Computación y Estadísticas.
Números Aleatorios.

El problema que estudiaremos es, entonces, escoger una fuente de números aleatorios y obtener a partir de esta suficientes números para nuestro experimentos de simulación.
Números Aleatorios.

Un método muy usado, hasta hace poco tiempo, Lehmer (1951).
Generadores Congrenciales

Para un multiplicador a.
Sesgo b.
Modulo m.
Semilla Xo.
Se asume que a, b e {0,1,…….,m-1}
Generadores Congrenciales

A pesar de su aparente simplicidad y previsibilidad, una sección cuidadosa de los parámetros (a, b, m) permite obtener de manera eficiente sucesiones de números suficientemente largas y aleatorias para algunos propósitos.
Si se representan por ejemplo de manera grafica los casos 4 y 5. de las salidas (Xi,Xi+1)
Generadores Congrenciales

1.- Un generador congruencial tiene ciclos.
2.- La longitud del ciclo del generador depende de la selección de los parámetros. Comparar longitud de los caso 1 y 3.
3.-Dentro de las selecciones de parámetros que conducen a una misma longitud de ciclo, algunas salidas parecen mas aleatorias que otras (compárense los casos 1 y 2).
4.- La representación de los pares (Xi, Xi+1) sugiere que estos se disponen en un numero finito de rectas.
Generadores Congruenciales

Existen varios métodos que nos permiten generar variables aleatorias. Lo normal es que existan varias opciones para generar una misma variable aleatoria. La elección del método adecuado se puede basar en una serie de factores como:
Exactitud, se prefiere un método exacto frente a métodos aproximados, como soluciones numéricas.
Velocidad. Uno de los datos que se toma en consideración es el el tiempo de generación de la variable.
Espacio. Necesidades de memoria del método utilizado. En general, los métodos no consumen mucha memoria.
Simplicidad.
La mayoría de las técnicas utilizadas para la generación se pueden agrupar en:
Método de la transformada inversa .
Método de aceptación-rechazo.
Método de composición.
Método de convolución.
Generacion de Variables Aleatorias

La generación de cualquier variable aleatoria se va a basar en la generación previa de una distribución uniforme U(0,1), Luego vamos a estudiar ciertas transformaciones o algoritmos que nos van a transformar dichos números generados en valores de otras distribuciones.
Generacion de Variables Aleatorias

La función de distribución (también llamada función de distribución acumulativa), F(x), de una variable aleatoria X es definida para cada número real x como sigue:
F(x)=P(X=x) para -8< x< 8
Una función de distribución F(x) tiene las siguientes propiedades:
0=F(x) =1.
F(x) es no decreciente (es decir, si x1< x2, entonces F(x1)< F(x2)).
lim F(x)=1 y lim F(x)=0 (ya que X sólo toma valores finitos).
Entonces sea U una variable aleatoria con distribución uniforme en (0,1). Entonces, la Variable aleatoria tiene función de distribución F.
Método de Inversión
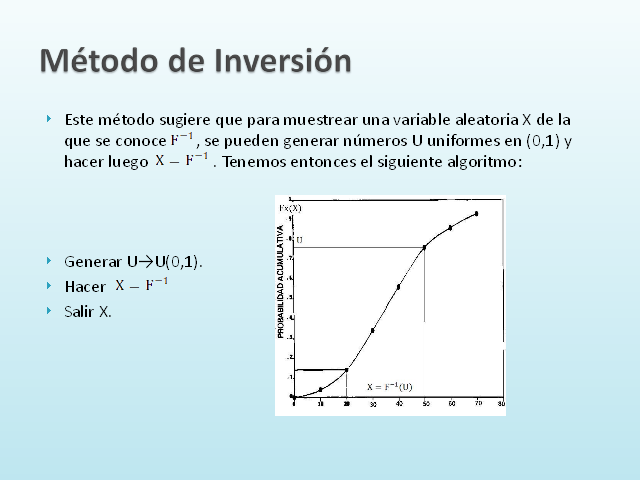
Este método sugiere que para muestrear una variable aleatoria X de la que se conoce , se pueden generar números U uniformes en (0,1) y hacer luego . Tenemos entonces el siguiente algoritmo:
Generar U?U(0,1).
Hacer
Salir X.
Método de Inversión

Este método sugiere que para muestrear una variable aleatoria X de la que se conoce , se pueden generar números U uniformes en (0,1) y hacer luego . Tenemos entonces el siguiente algoritmo:
Generar U?U(0,1).
Hacer
Salir X.
Método de Inversión

Generemos entonces una exponencial de parámetro ? = 1. Su función de distribución es:
Luego hacemos , o bien , ya que también .
Método de Inversión

Entonces una inversa exponencial de parámetro ? = 1, resulta en definitiva:
Generar U?U(0,1).
Hacer .
Salir X.
Método de Inversión

Otro ejemplo, una función triangular, Sea la función:
Método de Inversión

Luego la distribución resultante:
Método de Inversión

Supongamos que deseamos muestrear una variable aleatoria X con función de densidad f, No lo sabemos hacer directamente, pero disponemos de un procedimiento para muestrear de una función de densidad g tal que:
f(x)=ag(x), para todo x, siendo a< 8.
El método de rechazo sugiere Hasta que U = f(x)/ag(x)
Generar X »g
Generar U ˜U(0,1)
Fin hasta
Retornar X
Método de Rechazo

El método del rechazo equivale a generar valores
Y ˜ U(0,ag(x)) y aceptarlos si Y = f(y).
Ejemplo:
Generación de la variable aleatoria Be(3,4). Su función de densidad es:
f(x)= 60 x^2*(1-x) ^3. 0< x< 1
Método de Rechazo

Tomemos como g la densidad de la distribución uniforme entre (0,1)determinemos una constante a tal que f(x) = ag(x).
El máximo valor que alcanza la funcion f(x)/g(x), es 2/5. Luego:
Método de Rechazo

Luego el procedimiento de rechazo queda:
Generar .
Salir X=U1.
Método de Rechazo