
(Gp:) Germanio tipo P
(Gp:) Al
(Gp:) Al
(Gp:) Al
(Gp:) Al
(Gp:) Al
(Gp:) Al
(Gp:) Al
(Gp:) Al
(Gp:) Al
(Gp:) Al
(Gp:) Aceptador no ionizado
(Gp:) Germanio
(Gp:) 0 K
Ambos son neutros
Existe compensación de cargas e iones
(Gp:) hueco
electrón
(Gp:) +
(Gp:) –
(Gp:) –
(Gp:) +
(Gp:) Generación
térmica
(Gp:) Germanio
(Gp:) Donador ionizado
(Gp:) Germanio tipo N
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) Generación
térmica
(Gp:) Aceptador ionizado
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) 300 K

¿Qué pasaría si no existiera la barrera que impide la difusión?
(Gp:) Germanio tipo P
(Gp:) –
(Gp:) +
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) Barrera que impide la difusión
(Gp:) Germanio tipo N
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
Unión PN (I)

¿Se va a producir una difusión completa de huecos y electrones?
(Gp:) Al-
(Gp:) Al-
(Gp:) Germanio tipo P
(Gp:) –
(Gp:) +
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) Germanio tipo N
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) +
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
Unión PN (II)
(Gp:) +
(Gp:) +
(Gp:) –
(Gp:) –
Se produce difusión de huecos de la zona P hacia la zona N y de electrones de la zona N hacia la zona P

(Gp:) Al-
(Gp:) Al-
Germanio tipo P
(Gp:) –
(Gp:) +
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
Germanio tipo N
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) +
(Gp:) –
Unión PN (III)
(Gp:) +
(Gp:) +
(Gp:) –
(Gp:) –
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
¿Se va a producir una difusión completa de huecos y electrones?
¿Es esta situación la situación final?
NO
Zona P no neutra, sino cargada negativamente
Zona N no neutra, sino cargada positivamente

Aparece un campo eléctrico en la zona de contacto (unión metalúrgica) de las zonas
Unión PN (IV)
(Gp:) +
(Gp:) –
(Gp:) E
(Gp:) ?
(Gp:) Al-
(Gp:) Al-
(Gp:) Germanio tipo P
(Gp:) –
(Gp:) +
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) Germanio tipo N
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) +
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) +
(Gp:) +
(Gp:) –
(Gp:) –

El campo eléctrico limita el proceso de difusión
Unión PN (V)
Cercanías de la unión metalúrgica
(Gp:) Al-
(Gp:) Al-
(Gp:) Germanio tipo P
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Germanio tipo N
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) E
(Gp:) ?
Por difusión (® ¬)
Por campo eléctrico (¬®)
(Gp:) +
(Gp:) +
(Gp:) –
(Gp:) –

Zona de Transición
Existe carga espacial y no existen casi portadores de carga
(Gp:) Zona P NEUTRA (huecos compensados con “iones -”)
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) Al-
(Gp:) Al-
(Gp:) Sb+
(Gp:) Sb+
(Gp:) +
(Gp:) –
(Gp:) E
(Gp:) ?
(Gp:) Zona N NEUTRA
(electrones compensados con “iones +”)
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
Zonas de la unión PN (I)

(Gp:) Zona de Transición (no neutra)
Existe carga espacial (que genera campo eléctrico, E, y diferencia de potencial eléctrico, VO) y no existen casi portadores de carga
(Gp:) ?
Zonas de la unión PN (II)
Muchos huecos, pero neutra
Muchos electrones, pero neutra
(Gp:) Zona P
(neutra)
(Gp:) Zona N
(neutra)
(Gp:) + –
(Gp:) Unión metalúrgica
Muy
importante
(Gp:) E
(Gp:) ?
(Gp:) V0

(Gp:) – +
(Gp:) – +
(Gp:) – +
(Gp:) – +
(Gp:) – +
(Gp:) – +
(Gp:) – +
(Gp:) – +
(Gp:) ZONA P
(Gp:) ZONA N
Equilibrio de corrientes de la unión PN sin polarizar (I)
La corriente neta en cualquier sección del dispositivo debe ser cero
(Gp:) +
(Gp:) por campo
(Gp:) jp campo
(Gp:) +
(Gp:) por difusión
(Gp:) jp difusión
(Gp:) –
(Gp:) por campo
(Gp:) jn campo
(Gp:) –
(Gp:) por difusión
(Gp:) jn difusión
Se compensan
Se compensan

(Gp:) + –
+ –
+ –
+ –
(Gp:) – +
(Gp:) Zona N
(Gp:) Zona P
(Gp:) V0
Equilibrio de corrientes de la unión PN sin polarizar (II)
jp campo = – jp difusión
(Gp:) +
(Gp:) +
(Gp:) (concentración de huecos en la zona N) pN
(Gp:) +
(Gp:) pP (concentración de huecos en la zona P)
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +

jp difusión = -q·Dp·dp/dx
jp campo = q·?p·p·E
E = -dV/dx
Equilibrio de corrientes de la unión PN sin polarizar (III)
(Gp:) E
(Gp:) ?
jp campo = – jp difusión
Ecuaciones:
Por tanto: dV = -(Dp/mp)·dp/p
Finalmente, integrando se obtiene:
V0 = Vborde_zona_N – Vborde_zona_P = -(Dp/?p)·ln(pN/pP) Þ
V0 = (Dp/?p)·ln(pP/pN)
(Gp:) borde_zona_P
(Gp:) borde_zona_N

(Gp:) + –
+ –
+ –
+ –
(Gp:) – +
(Gp:) Zona P
(Gp:) Zona P
(Gp:) V0
Equilibrio de corrientes de la unión PN sin polarizar (IV)
(Gp:) (concentración de electrones en la zona N) nN
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) nP (concentración de electrones en la zona P)
(Gp:) –
(Gp:) –
(Gp:) –
jn campo = -jn difusión

jn difusión = q·Dn·dn/dx
jn campo = q·?n·n·E
E = -dV/dx
Equilibrio de corrientes de la unión PN sin polarizar (V)
(Gp:) E
(Gp:) ?
jn campo = – jn difusión
Ecuaciones:
Por tanto: dV = (Dn/mn)·dn/n
Finalmente, integrando se obtiene:
V0 = Vborde_zona_N – Vborde_zona_P = (Dn/?n)·ln(nN/nP)
(Gp:) borde_zona_P
(Gp:) borde_zona_N

(Gp:) + –
+ –
+ –
+ –
(Gp:) – +
Zona N
Zona P
V0
Resumen del equilibrio de corrientes de la unión PN sin polarizar
(Gp:) pN
(Gp:) +
(Gp:) pP
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) –
(Gp:) –
Zona P
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) nN
(Gp:) –
(Gp:) nP
V0 = (Dn/?n)·ln(nN/nP) y también V0 = (Dp/?p)·ln(pP/pN)

(Gp:) Zona P
(Gp:) Zona N
(Gp:) + –
(Gp:) V0
Ecuación del equilibrio de las corrientes de electrones:
V0= (Dn/?n)·ln(nN/nP) = (Dn/?n)·ln(ND·NA/ni2)
(Gp:) Si NA >> ni
pP = NA nP = ni2/NA
(Gp:) NA, pP, nP
(Gp:) Si ND >> ni
nN = ND pN = ni2/ND
(Gp:) ND, nN, pN
Cálculo de la tensión de contacto V0 (I)
Ecuación del equilibrio de las corrientes de huecos:
V0 = (Dp/?p)·ln(pP/pN) = (Dp/?p)·ln(NA·ND/ni2)
Por tanto:
Dp/?p = Dn/?n

(Gp:) Zona P
(Gp:) Zona N
(Gp:) + –
(Gp:) V0
(Gp:) pP » NA nP = ni2/NA
(Gp:) NA, pP, nP
(Gp:) nN » ND pN = ni2/ND
(Gp:) ND, nN, pN
Cálculo de la tensión de contacto V0 (II)
Muy
importante
(VT = 26mV a 300 K)
La cantidad Dp/?p = Dn/?n vale (no demostrado aquí):
Dp/?p = Dn/?n = kT/q = VT (Relación de Einstein), donde:
k = constante de Boltzmann
T = temperatura absoluta
Por tanto:
V0 = VT·ln(pP/pN)
V0 = VT·ln(nN/np)
(Gp:) nN/nP = e
(Gp:) V0/ VT
(Gp:) pP/pN = e
(Gp:) V0/ VT
(Gp:) ó

(Gp:) ?(x)
(Gp:) Densidad de carga
(Gp:) x
(Gp:) Zona P
(Gp:) Zona N
(Gp:) –
(Gp:) +
(Gp:) E(x)
(Gp:) V0
(Gp:) Teorema de Gauss: ·E(x) = ?(x)/e
(Gp:) ?
(Gp:) -Emax0
(Gp:) Campo eléctrico
(Gp:) E(x)
(Gp:) x
(Gp:) VU(x)
(Gp:) V0
(Gp:) Tensión
(Gp:) x
(Gp:) Diferencia de potencial:
E(x) = – V
(Gp:) ?
(Gp:) Relaciones entre r, E y V0

(Gp:) Zona P
(Gp:) Zona N
(Gp:) –
(Gp:) +
(Gp:) x
(Gp:) E(x)
(Gp:) -Emax0
(Gp:) ?(x)
(Gp:) x
(Gp:) Situación real
(Gp:) -q·NA
(Gp:) q·ND
(Gp:) Hipótesis de vaciamiento
Se admite que:
Hay cambio brusco de zona P a zona N
No hay portadores en la zona de transición
Unión abrupta e hipótesis de vaciamiento

(Gp:) Unión metalúrgica
(Gp:) Zona P
(Gp:) Zona N
(Gp:) LZT0
La neutralidad de la carga total en la zona de transición exige:
NA·LZTP0 = ND·LZTN0
(Gp:) LZTN0
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) Sb+
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) ND
(Gp:) LZTP0
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) Al-
(Gp:) +
(Gp:) NA
(Gp:) +
La zona de transición cuando NA< ND
En la zona más dopada hay menos zona de transición

(Gp:) Zona P
(Gp:) Zona N
(Gp:) –
(Gp:) +
(Gp:) E(x)
(Gp:) +
(Gp:) –
(Gp:) VO
(Gp:) E(x)
(Gp:) -Emax0
(Gp:) Campo eléctrico
(Gp:) x
(Gp:) Relaciones entre r, E y V0 cuando NA < ND
(Gp:) ?(x)
(Gp:) Densidad de carga
(Gp:) x
(Gp:) q·ND
(Gp:) -q·NA
(Gp:) VU(x)
(Gp:) V0
(Gp:) Tensión
(Gp:) x

Equilibrio difusión-campo en la zona de transición:
V0 = VT·ln(NA·ND/ni2) (1) VT = k·T/q, 26mV a 300 K
Neutralidad neta entre ambas partes de la zona de transición:
NA·LZTP0 = ND·LZTN0 (2)
Longitud total de la zona de transición:
LZT0 = LZTP0+ LZTN0 (3)
Relaciones entre las partes de la zona de transición (partiendo de (2) y (3) ):
LZTP0 = LZT0·ND/(NA+ND) (4) LZTN0 = LZT0·NA/(NA+ND) (5)
Ecuaciones en equilibrio (sin polarizar) (I)

(Gp:) V0 = -area limitada por E(x) = (LZTP0+ LZTN0)·Emax0/2 (7)
(Gp:) Definición de diferencia de potencial: E(x) = – VU(x)
(Gp:) ?
(Gp:) VU(x)
(Gp:) V0
(Gp:) x
(Gp:) VU(x) = – E(x)·dx
(Gp:) -LZTP0
(Gp:) x
Teorema de Gauss en la zona de transición:
(Gp:) E(0) = -Emax0 = -LZTN0·q·ND/??= -LZTP0·q·NA/? (6)
(Gp:) -Emax0
Ecuaciones en equilibrio (sin polarizar) (II)
(Gp:) E(x)
(Gp:) x
(Gp:) 0
(Gp:) LZTP0
(Gp:) E(x) = -(LZTP0+x)·q·NA/???????(zona P)
(Gp:) LZTN0
(Gp:) E(x) = -(LZTN0-x)·q·ND/? (zona N)

Ecuaciones en equilibrio (sin polarizar) (III)
partiendo de (3-7) se obtiene:
V0 = q·L2ZT0·NA·ND·/[2·?·(NA+ND)] (8)
Teniendo en cuenta (1) y eliminando V0 se obtiene:
(Gp:) 2·?·(NA+ND)·VT·ln(NA·ND/ni2)
(Gp:) LZT0 =
(Gp:) q·NA·ND
(Gp:) (9)
Partiendo de (4-6) se obtiene:
Emax0 = q·LZT0·ND·NA/[(NA+ND)·?] (10)
y eliminando LZT0 entre (8) y (10) se obtiene:
(Gp:) ?·(NA+ND)
(Gp:) Emax0=
(Gp:) 2·q·NA·ND·V0
(Gp:) (11)

Ecuaciones en equilibrio (sin polarizar) (IV)
(Gp:) 2·?·(NA+ND)·VT·ln(NA·ND/ni2)
(Gp:) LZT0 =
(Gp:) q·NA·ND
(Gp:) (9)
(Gp:) ?·(NA+ND)
(Gp:) Emax0 =
(Gp:) 2·q·NA·ND·V0
(Gp:) (11)
V0 = VT·ln(NA·ND/ni2) (1)
(Gp:) 2·?·(NA+ND)·V0
(Gp:) LZT0 =
(Gp:) q·NA·ND
(Gp:) (9)’
Resumen
Muy
importante

Ecuaciones en equilibrio (sin polarizar) (V)
(Gp:) 2·?·(NA+ND)·VT·ln(NA·ND/ni2)
(Gp:) LZT0 =
(Gp:) q·NA·ND
(Gp:) ?·(NA+ND)
(Gp:) Emax0 =
(Gp:) 2·q·NA·ND·V0
V0 = VT·ln(NA·ND/ni2)
Conclusiones importantes
Muy
importante
(Gp:) V0 crece con el productos de los dopados, pero crece poco
(Gp:) LZT0 decrece con los dopados
(Gp:) Basta con que un dopado sea pequeño para que Emax0 sea pequeño

Luego:
V = 0, i = 0
Por tanto:
VmP – V0 + VNm = 0
y
VmP + VNm = V0
(Gp:) V0
(Gp:) –
(Gp:) +
(Gp:) P
(Gp:) N
(Gp:) + –
(Gp:) VmP
(Gp:) –
(Gp:) +
(Gp:) VNm
(Gp:) –
(Gp:) +
(Gp:) V = 0
(Gp:) I = 0
(Gp:) No se puede estar disipando energía si no llega energía al dispositivo
La unión PN polarizada (I)
Conclusión:
Los potenciales de contacto de las uniones metal-semiconductor tienen que compensar el potencial de contacto de la unión semiconductora

V = VmP – VU + VNm = V0 – VU
Luego:
VU = V0 – V
(Gp:) VU
(Gp:) –
(Gp:) +
(Gp:) VmP
(Gp:) –
(Gp:) +
(Gp:) VNm
(Gp:) –
(Gp:) +
(Gp:) i ? 0
(Gp:) P
(Gp:) N
(Gp:) + –
(Gp:) V
(Gp:) –
(Gp:) +
(Gp:) Baja resistividad:
VN=0
(Gp:) Baja resistividad:
VP=0
La unión PN polarizada (II)
Hipótesis (bastante real): los potenciales de los contactos metal-semiconductor no varían con relación al caso anterior (VmP+VNm= VO)
Polarización directa
El potencial de contacto de la unión semiconductora disminuye en el valor V

V = -VmP + VU – VNm = -V0 + VU
Luego:
VU = V0 + V
(Gp:) VU
(Gp:) –
(Gp:) +
(Gp:) VmP
(Gp:) –
(Gp:) +
(Gp:) VNm
(Gp:) –
(Gp:) +
(Gp:) i ? 0
(Gp:) P
(Gp:) N
(Gp:) + –
(Gp:) V
(Gp:) –
(Gp:) +
(Gp:) Baja resistividad:
VN=0
(Gp:) Baja resistividad:
VP=0
La unión PN polarizada (III)
Polarización inversa
El potencial de contacto de la unión semiconductora aumenta en el valor V

VU = V0 – V,
Con la limitación V < V0
La unión PN polarizada (IV)
Notación a usar en general
(Gp:) V
(Gp:) –
(Gp:) +
(Gp:) =
(Gp:) VU
(Gp:) –
(Gp:) +
(Gp:) P
(Gp:) N
(Gp:) + –
(Gp:) i
(“aparcamos” la posibilidad real de que V >V0)
Conclusión:
siempre VU = V0 – V, siendo
Polarización directa: 0 < V < V0
Polarización inversa: V < 0
Muy
importante

La unión PN polarizada (V)
¿Cómo se modifica la longitud de la zona de transición, y la intensidad máxima del campo eléctrico?
Regla general (válida para V < V0):
Sustituir V0 por (V0-V) en las ecuaciones:
(Gp:) ?·(NA+ND)
(Gp:) Emax0 =
(Gp:) 2·q·NA·ND·V0
(Gp:) LZT0 =
(Gp:) 2·?·(NA+ND)·V0
(Gp:) q·NA·ND

La unión PN polarizada (VI)
(Gp:) ?·(NA+ND)
(Gp:) Emax0 =
(Gp:) 2·q·NA·ND·V0
(Gp:) LZT0 =
(Gp:) 2·?·(NA+ND)·V0
(Gp:) q·NA·ND
(Gp:) Sin polarizar teníamos:
(Gp:) Emax =
(Gp:) ?·(NA+ND)
(Gp:) 2·q·NA·ND·(V0-V)
(Gp:) LZT =
(Gp:) 2·?·(NA+ND)·(V0-V)
(Gp:) q·NA·ND
(Gp:) Con polarización tenemos:
Polarización directa (0 < V < V0):
LZT y Emax disminuyen
Polarización inversa (V < 0):
LZT y Emax aumentan
Muy
importante

(Gp:) Zona P
(Gp:) –
(Gp:) +
(Gp:) Zona N
(Gp:) V0
(Gp:) LZT0
(Gp:) ?(x)
(Gp:) x
(Gp:) E(x)
(Gp:) -Emax0
(Gp:) x
(Gp:) VU(x)
(Gp:) V0
(Gp:) x
(Gp:) -Emax
(Gp:) V0-Vext
(Gp:) Relaciones entre r, E y V0 con polarización directa
Menos carga espacial
Menor intensidad de campo
Menor potencial de contacto
(Gp:) V0-Vext
(Gp:) Zona P
(Gp:) –
(Gp:) +
(Gp:) Zona N
(Gp:) Vext
(Gp:) LZT

(Gp:) Zona P
(Gp:) –
(Gp:) +
(Gp:) Zona N
(Gp:) V0
(Gp:) LZT0
(Gp:) Relaciones entre r, E y VO con polarización inversa
(Gp:) ?(x)
(Gp:) x
(Gp:) E(x)
(Gp:) -Emax0
(Gp:) x
(Gp:) VU(x)
(Gp:) V0
(Gp:) x
(Gp:) V0+Vext
(Gp:) -Emax
(Gp:) V0+Vext
(Gp:) Vext
(Gp:) Zona P
(Gp:) –
(Gp:) +
(Gp:) Zona N
(Gp:) LZT
Más carga espacial
Mayor intensidad de campo
Mayor potencial de contacto

Polarización directa:
Disminuye la tensión interna que frena la difusión
Disminuye el campo eléctrico en la zona de transición
Disminuye el ancho de la zona de transición
Polarización inversa:
Aumenta la tensión interna que frena la difusión
Aumenta el campo eléctrico en la zona de transición
Aumenta el ancho de la zona de transición
Conclusiones parciales
Muy
importante

¿Qué pasa con la concentración de portadores cuando se polariza? Ejemplo: electrones en polarización directa
nN
nP
V0 = VT·ln(nN/nP)
(Gp:) – +
(Gp:) Zona P
(Gp:) Zona P
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) + –
+ –
+ –
+ –
V0
V0-V =VT·ln(nNV/nPV)
nNV
nPV
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
(Gp:) –
V0-V
nNV/nPV cambia mucho

Electrones:
V0 – V = VT·ln(nNV/nPV)
Concentración de portadores con polarización (I)
Analizamos la situación en los bordes externos de la zona de transición:
En zona P: DpP = pPV – pP DnP = nPV – nP
En zona N: DnN = nNV – nN DpN = pNV – pN
Por neutralidad de carga (aproximada):
DpP » DnP DnN » DpN
Como pP >> nP y nN >> pN y admitimos que pP >> DpP y nN >> DnN (hipótesis de baja inyección), se cumple:
pPV/pNV = (pP + DpP) /pNV » pP/pNV
nNV/nPV = (nN + DnN) /nPV » nN/nPV
Huecos:
V0 – V = VT·ln(pPV/pNV)
Es como si los mayoritarios no cambiaran de concentración

Cambio de la concentración de electrones a los dos lados de la zona de transición:
VU = V0 – V = VT·ln(nN/nPV)
Concentración de portadores con polarización (II)
Cambio de la concentración de huecos a los dos lados de la zona de transición:
VU = V0 – V = VT·ln(pP/pNV)
(Gp:) nPV = nN·e
(Gp:) -VU/ VT
(Gp:) pNV = pP·e
(Gp:) -VU/ VT
(Gp:) V
(Gp:) –
(Gp:) +
(Gp:) =
(Gp:) VU
(Gp:) –
(Gp:) +
(Gp:) Zona P
(Gp:) Zona N
(Gp:) + –
(Gp:) pP = NA
(Gp:) nN = ND
(Gp:) pNV = NA·e
(Gp:) -VU/ VT
Por tanto:
(Gp:) nPV = ND·e
(Gp:) -VU/ VT

(Gp:) Hemos llegado a:
V0 – V = VT·ln(nN/nPV)
(Gp:) Hemos llegado a:
V0 – V = VT·ln(pP/pNV)
(Gp:) Partíamos de:
V0 = VT·ln(nN/nP)
(Gp:) Partíamos de:
V0 = VT·ln(pP/pN)
(Gp:) Y esta fórmula venía de:
jn campo + jn difusión = jn total = 0
(Gp:) Y esta fórmula venía de:
jp campo + jp difusión = jp total = 0
Pero con polarización jp total ¹ 0 y jn total ¹ 0. Por tanto, las expresiones mostradas no son válidas con polarización. Sin embargo, se pueden seguir usando como una aproximación razonable ya que en la unión:
jp total < < jp campo jp total < < jp difusión
jn total < < jn campo jn total < < jn difusión
¡¡¡Ojo!!!
Hay una pequeña “trampa”

(Gp:) 0,313?m
(Gp:) Dp=50 cm2/s Dn=100 cm2/s ni=2,5·1013 port/cm3
?p=1900 cm2/V·s ?n=3900 cm2/V·s ?r=16
Lp=0,22 mm Ln=0,32 mm ?p= ?n= 10 ?s
(Gp:) Datos del Ge a 300 K
(Gp:) pP
(Gp:) pN
(Gp:) nN
(Gp:) nP
(Gp:) 1010
(Gp:) 1012
(Gp:) 1014
(Gp:) 1016
(Gp:) Portad./cm3
(Gp:) 1?m
(Gp:) -1?m
(Gp:) 0
V0=0,31 V
Ejemplo 1: unión de Germanio sin polarizar
(Gp:) NA=1016 atm/cm3
(Gp:) varios mm
(Gp:) P
(Gp:) N
(Gp:) + –
(Gp:) ND=1016 atm/cm3

Ejemplo 1 con polarización directa
(Gp:) V0=0,31 V
(Gp:) 0,313?m
(Gp:) varios mm
(Gp:) P
(Gp:) N
(Gp:) + –
(Gp:) nN
(Gp:) nP
(Gp:) pP
(Gp:) pN
(Gp:) 1010
(Gp:) 1012
(Gp:) 1014
(Gp:) 1016
(Gp:) Portad./cm3
(Gp:) 1?m
(Gp:) -1?m
(Gp:) 0
(Gp:) V=180mV
(Gp:) VU =0,13 V
(Gp:) 0,215?m
(Gp:) P
(Gp:) N
(Gp:) – +
(Gp:) pNV
(Gp:) nPV
(Gp:) En esta parte del cristal se produce un aumento muy fuerte de los minoritarios
VU = 0,31-0,18 = 0,13 V

Ejemplo 1 con polarización inversa
(Gp:) V0=0,31 V
(Gp:) 0,313?m
(Gp:) varios mm
(Gp:) P
(Gp:) N
(Gp:) + –
(Gp:) nN
(Gp:) nP
(Gp:) pP
(Gp:) pN
(Gp:) V=180mV
(Gp:) VU =0,49 V
(Gp:) 0,416?m
(Gp:) P
(Gp:) N
(Gp:) – +
(Gp:) 1010
(Gp:) 1012
(Gp:) 1014
(Gp:) 1016
(Gp:) Portad./cm3
(Gp:) 1?m
(Gp:) -1?m
(Gp:) 0
(Gp:) 108
(Gp:) nPV
(Gp:) pNV
VU = 0,31+0,18 = 0,49 V
(Gp:) En esta parte del cristal se produce una disminución muy fuerte de los minoritarios

¿Cómo evoluciona la concentración de minoritarios en las zonas alejadas de la unión? Ejemplo: huecos en zona N con polarización directa
(Gp:) Zona de transición
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) Zona N
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
(Gp:) +
Inyección continua de minoritarios a través de una sección (ATE-UO Sem 40 y ATE-UO Sem 41)
(Gp:) x
(Gp:) 0
(Gp:) pNV(x)
(Gp:) pNV?
(Gp:) pNV0

(Gp:) pNV
(Gp:) nPV
(Gp:) nN
(Gp:) nP
(Gp:) 1010
(Gp:) 1012
(Gp:) 1014
(Gp:) 1016
(Gp:) Portad./cm3
(Gp:) Esc. log.
(Gp:) 1016
(Gp:) 5·1015
(Gp:) 0
(Gp:) Por./cm3
(Gp:) Escala
lineal
(Gp:) Zona P
(Gp:) Zona N
(Gp:) nPV
(Gp:) nN
(Gp:) nP
(Gp:) pP
(Gp:) pN
(Gp:) pP
(Gp:) pN
(Gp:) pNV
(Gp:) nPV
(Gp:) nN
(Gp:) nP
(Gp:) pP
(Gp:) pN
(Gp:) pNV
(Gp:) V=180mV
(Gp:) Zona P
(Gp:) Zona N
(Gp:) V=180mV
(Gp:) Portad./cm3
(Gp:) 1010
(Gp:) 1012
(Gp:) 1014
(Gp:) 1016
(Gp:) 108
(Gp:) Esc. log.
Concentraciones en zonas alejadas de la unión

(Gp:) Zona P
(Gp:) Zona N
(Gp:) nPV
(Gp:) pNV
(Gp:) pN
(Gp:) nP
(Gp:) Portad./cm3
(Gp:) Longitud [mm]
(Gp:) 8·1013
(Gp:) 4·1013
(Gp:) 0
(Gp:) -3
(Gp:) -2
(Gp:) -1
(Gp:) 0
(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) Zona P
(Gp:) Zona N
(Gp:) pN
(Gp:) nP
(Gp:) 8·1010
(Gp:) 4·1010
(Gp:) 0
(Gp:) -3
(Gp:) -2
(Gp:) -1
(Gp:) 0
(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) Portad./cm3
(Gp:) Longitud [mm]
Concentración de minoritarios en zonas alejadas de la unión (zonas neutras) en escala lineal
(Gp:) V=180mV
(Gp:) V=180mV
(Gp:) nPV
(Gp:) pNV
El aumento de concentración diminuye exponencialmente al alejarse de la unión
La disminución de concentración diminuye exponencialmente al alejarse de la unión
¡Ojo con las escalas!

Exceso de concentración en las zonas neutras y gradiente de minoritarios en los bordes de la zona de transición (I)
Debido a los diferentes valores de las escalas de concentraciones, los valores del exceso de carga y del gradiente son muy distintos
(Gp:) pNV
(Gp:) Portad./cm3
(Gp:) Longitud [mm]
(Gp:) 8·1013
(Gp:) 4·1013
(Gp:) 0
(Gp:) -3
(Gp:) -2
(Gp:) -1
(Gp:) 0
(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) nPV
(Gp:) Polarización directa
(Gp:) 8·1010
(Gp:) 4·1010
(Gp:) 0
(Gp:) -3
(Gp:) -2
(Gp:) -1
(Gp:) 0
(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) Portad./cm3
(Gp:) Longitud [mm]
(Gp:) nPV
(Gp:) pNV
(Gp:) Polarización inversa
(Gp:) Alto gradiente
(Gp:) Pequeño gradiente
(Gp:) Alto exceso de minoritarios
(Gp:) Escaso exceso de minoritarios
¡Ojo con las escalas!

(Gp:) 8·1013
(Gp:) 4·1013
(Gp:) 0
(Gp:) Portad./cm3
(Gp:) Zona N
(Gp:) Zona P
(Gp:) pN
(Gp:) nP
(Gp:) nPV
(Gp:) V=180mV
(pol. directa)
(Gp:) pNV
(Gp:) nPV
(Gp:) pNV
(Gp:) V=-180mV
(pol. inversa)
Exceso de concentración en las zonas neutras y gradiente de minoritarios en los bordes de la zona de transición (II)
Aquí se ve mejor

¿Por qué tanto interés en la evolución de la concentración de los minoritarios en los bordes externos de la zona de transición?
Porque dicha evolución es la clave para deducir la relación entre la tensión V y la corriente i en una unión PN polarizada, que es lo que realmente nos interesa.
(Gp:) V
(Gp:) –
(Gp:) +
(Gp:) =
(Gp:) P
(Gp:) N
(Gp:) + –
(Gp:) i

¿Cómo calcular la corriente (I)?
(Gp:) varios mm
(Gp:) V
(Gp:) VU
(Gp:) 0,215?m
(Gp:) P
(Gp:) N
(Gp:) – +
(Gp:) Zona P
(Gp:) Zona N
¿Analizando la zona de transición?
En la zona de transición hay gradientes de concentración e intensidades de campo eléctrico muy grandes, que causan que:
jp total< < jp campo jp total< < jp difusión jn total< < jn campo jn total< < jn difusión
(Gp:) Portad./cm3
(Gp:) nP
(Gp:) pN
(Gp:) 1014
(Gp:) 1016
(Gp:) pNV
(Gp:) nPV
(Gp:) Esc. log.
(Gp:) 1mm
No es posible obtener información sobre la corriente total por este método

¿Cómo calcular la corriente (II)?
¿Analizando los mayoritarios de las zonas “neutras”?
(Gp:) V
(Gp:) 3 mm
(Gp:) P
(Gp:) N
(Gp:) – +
(Gp:) Zona P
(Gp:) Escala lineal
(Gp:) Portad./cm3
(Gp:) 1016 + 8·1013
(Gp:) 0
(Gp:) pPV
(Gp:) 1016 + 4·1013
(Gp:) 1016
(Gp:) pP
Sabemos que los mayoritarios aumentan aproximadamente así, por lo que podríamos calcular la corriente de difusión de mayoritarios
Pero no podemos calcular la corriente debida a campo eléctrico (de arrastre) ya que no sabemos lo que vale el campo (aunque sí sabemos que es muy pequeño)
Tampoco vale este método
¡Ojo con la escala!

¿Cómo calcular la corriente (III)?
(Gp:) 6 mm
(Gp:) V
(Gp:) 0,215?m
(Gp:) P
(Gp:) N
(Gp:) – +
(Gp:) Zona P
(Gp:) Zona N
(Gp:) Portad./cm3
(Gp:) 8·1013
(Gp:) 4·1013
(Gp:) 0
(Gp:) nPV
(Gp:) 6,25·1010
(Gp:) Esc. lin.
¿Analizando los minoritarios de las zonas “neutras”?
La corriente de minoritarios debida a campo eléctrico es despreciable (pequeños valores del campo y pequeña concentración)
La corriente significativa es la corriente de minoritarios debida a difusión
(Gp:) Portad./cm3
(Gp:) pNV
(Gp:) 8·1013
(Gp:) 4·1013
(Gp:) 0
(Gp:) Esc. lin.
(Gp:) 6,25·1010

¿Cómo calcular la corriente (IV)?
Cálculo de la corriente de minoritarios en las zonas “neutras”
(Gp:) Portad./cm3
(Gp:) pNV
(Gp:) 6,25·1010
(Gp:) Portad./cm3
(Gp:) nPV
(Gp:) 6,25·1010
(Gp:) 8·1013
(Gp:) 4·1013
(Gp:) 0
(Gp:) V
(Gp:) – +
(Gp:) Zona P
(Gp:) Zona N
(Gp:) 40
(Gp:) 20
(Gp:) 0
(Gp:) Densidad de corriente [mA/cm2]
(Gp:) jnP
(Gp:) jpN
(Gp:) jnP = q·Dn·dnPV/dx
(Gp:) jnP
(Gp:) jpN = -q·Dp·dpNV/dx
(Gp:) jpN

¿Cómo calcular la corriente (V)?
¿Podemos conocer la corriente total a partir de la corriente de minoritarios en las zonas “neutras”?
(Gp:) ¿Qué pasa en la zona de transición?
(Gp:) jnP
(Gp:) Longitud [mm]
(Gp:) 40
(Gp:) 20
(Gp:) 0
(Gp:) Densidad de corriente [mA/cm2]
(Gp:) 0-
(Gp:) -1.5
(Gp:) -1
(Gp:) -0.5
(Gp:) 0.5
(Gp:) 1
(Gp:) 1.5
(Gp:) 0+
Al no haber recombinaciones en la zona de transición, no se modifican las corrientes
(Gp:) jpN
(Gp:) V=180mV
(Gp:) Zona P
(Gp:) Zona N
(Gp:) jnP
(Gp:) jpN

¿Cómo calcular la corriente (VI)?
(Gp:) jnP
(Gp:) jpN
(Gp:) Longitud [mm]
(Gp:) 40
(Gp:) 20
(Gp:) 0
(Gp:) Densidad de corriente [mA/cm2]
(Gp:) 0-
(Gp:) -1.5
(Gp:) -1
(Gp:) -0.5
(Gp:) 0.5
(Gp:) 1
(Gp:) 1.5
(Gp:) 0+
(Gp:) 60
(Gp:) 80
En la zona de transición:
jtotal = jnP(0) + jpN(0)
En el resto del cristal:
La corriente tiene que ser la misma
(Gp:) jpN(0)
(Gp:) jnP(0)
(Gp:) jtotal = jnP(0) + jpN(0)
Muy, muy
importante
(Gp:) V=180mV
(Gp:) Zona P
(Gp:) Zona N
(Gp:) jnP
(Gp:) jpN
(Gp:) jtotal

1ª conclusión importantísima:
– Basta conocer la concentración de los minoritarios en los bordes de la zona de transición para conocer la corriente total
2ª conclusión importantísima:
Polarización directa:
El gradiente de dicha concentración es bastante grande Þ Corriente total bastante grande
Polarización inversa:
El gradiente de dicha concentración es muy pequeño Þ Corriente total muy pequeña

(Gp:) jnP
(Gp:) jpN
(Gp:) Longitud [mm]
(Gp:) 40
(Gp:) 20
(Gp:) 0
(Gp:) Densidad de corriente [mA/cm2]
(Gp:) 0-
(Gp:) -1.5
(Gp:) -1
(Gp:) -0.5
(Gp:) 0.5
(Gp:) 1
(Gp:) 1.5
(Gp:) 0+
(Gp:) 60
(Gp:) 80
(Gp:) jtotal
(Gp:) V=180mV
(Gp:) Zona P
(Gp:) Zona N
(Gp:) jtotal
jpP = jtotal – jnP
jnN = jtotal – jpN
Cálculo de la corriente debida a los mayoritarios
En cada zona “neutra” , todo lo que no es corriente de minoritarios es corriente de mayoritarios. Por tanto:
(Gp:) jnN
(Gp:) jpP
La corriente de mayoritarios se obtiene por diferencia entre corriente total y corriente de minoritarios
(Gp:) jpN
(Gp:) jpP
(Gp:) 0
(Gp:) 20
(Gp:) 40
(Gp:) 60
(Gp:) Densidad de corriente [mA/cm2]
(Gp:) jnP
(Gp:) jnN
(Gp:) jtotal
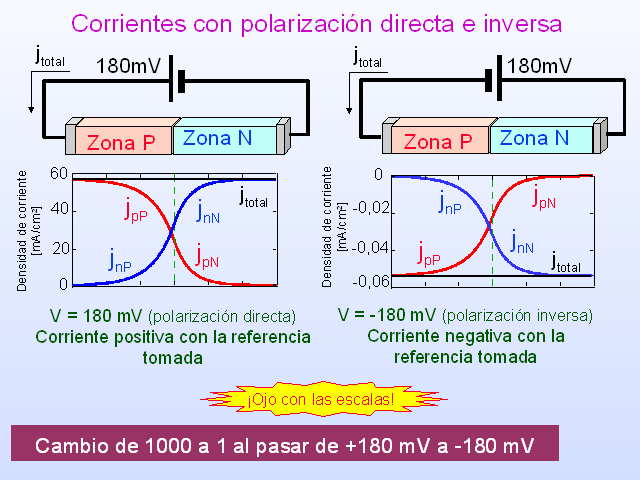
V = 180 mV (polarización directa)
Corriente positiva con la referencia tomada
(Gp:) jpN
(Gp:) jpP
(Gp:) jnP
(Gp:) jnN
(Gp:) jtotal
(Gp:) 0
(Gp:) -0,02
(Gp:) -0,04
(Gp:) -0,06
(Gp:) Densidad de corriente [mA/cm2]
V = -180 mV (polarización inversa)
Corriente negativa con la referencia tomada
Cambio de 1000 a 1 al pasar de +180 mV a -180 mV
(Gp:) 180mV
(Gp:) jtotal
(Gp:) Zona N
(Gp:) Zona P
(Gp:) Zona N
(Gp:) Zona P
(Gp:) 180mV
(Gp:) jtotal
Corrientes con polarización directa e inversa
¡Ojo con las escalas!

1- Se calcula el salto de concentración de cada tipo de portador de un extremo al otro de la zona de transición.
2- Se calcula el exceso de minoritarios en los bordes externos de la zona de transición.
3- Se calcula la distribución exponencial de los minoritarios al lo largo de las zonas neutras.
4- Se calcula el gradiente de dicha concentración justo en los bordes de la zona de transición.
5- Se calculan las densidades de corriente de minoritarios en los bordes de la zona de transición (densidad de corriente de huecos en el borde de la zona N y de electrones en el borde de la zona P).
6- La suma de las dos densidades de corriente anteriores es la densidad de corriente total.
7- La corriente total es la densidad de corriente por la sección.
Cálculo de la corriente en función de la tensión (I)

Cálculo de la corriente en función de la tensión (II)
(Gp:) 1010
(Gp:) 1012
(Gp:) 1014
(Gp:) 1016
(Gp:) pP
(Gp:) pNV(x)
(Gp:) Portad./cm3
(Gp:) -3
(Gp:) -2
(Gp:) -1
(Gp:) 0
(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) Longitud [mm]
(Gp:) pNV(0)
(Gp:) pN(?)
1- Se calcula el salto de concentración de cada tipo de portador de un extremo al otro de la zona de transición. Este salto depende de V0-V
2- Se calcula el exceso de minoritarios en los bordes externos de la zona de transición. Este exceso depende de V

Cálculo de la corriente en función de la tensión (III)
(Gp:) 1010
(Gp:) 1012
(Gp:) 1014
(Gp:) 1016
(Gp:) pP
(Gp:) pNV(x)
(Gp:) Portad./cm3
(Gp:) -3
(Gp:) -2
(Gp:) -1
(Gp:) 0
(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) Longitud [mm]
(Gp:) pNV(0)
(Gp:) pN(?)
3- Se calcula la distribución exponencial de los minoritarios al lo largo de las zonas neutras.
4- Se calcula el gradiente de dicha concentración justo en los bordes de la zona de transición (tga).
(Gp:) a

(Gp:) jnP
(Gp:) jpN
(Gp:) Longitud [mm]
(Gp:) 40
(Gp:) 20
(Gp:) 0
(Gp:) Densidad de corriente [mA/cm2]
(Gp:) 0-
(Gp:) -1.5
(Gp:) -1
(Gp:) -0.5
(Gp:) 0.5
(Gp:) 1
(Gp:) 1.5
(Gp:) 0+
(Gp:) 60
(Gp:) 80
Cálculo de la corriente en función de la tensión (IV)
5- Se calculan las densidades de corriente de minoritarios en los bordes de la zona de transición (densidades de corriente de huecos en el borde de la zona N y de electrones en el borde de la zona P).
(Gp:) jpN(0)
(Gp:) jnP(0)
6- La suma de las dos densidades de corriente anteriores es la densidad de corriente total.
(Gp:) jtotal = jnP(0) + jpN(0)
7- La corriente total es la densidad de corriente por la sección.
i = jtotal ·A

Cálculo de la corriente en función de la tensión (V)
El resultado final del cálculo es:
i = IS·(eV/VT – 1), siendo:
IS = A·q·ni2·[Dp/(ND·Lp)+Dn/(NA·Ln)]
(Is es corriente inversa de saturación dela unión PN)
VT = kT/q, donde:
A = sección de paso de la corriente (sección de la unión PN)
q = carga del electrón
ni = concentración intrínseca
Dp = constante de difusión de huecos
Dn = constante de difusión de electrones
Lp?= longitud de difusión de los huecos en la zona N
Ln?= longitud de difusión de los electrones en la zona P
ND = concentración de donador
NA = concentración de aceptador
k = constante de Boltzmann
T = temperatura absoluta
Muy, muy
importante
(Gp:) P
(Gp:) N
(Gp:) +
(Gp:) –
(Gp:) i
(Gp:) V

Polarización directa con VO > V >> VT
Polarización inversa con V < < -VT
(Gp:) Resumen:
(Gp:) i = IS·(e -1)
(Gp:) V
(Gp:) VT
(Gp:) donde:
(Gp:) VT = k·T/q = 26 mV
(Gp:) IS = A·q·ni2·[Dp/(ND·Lp)+Dn/(NA·Ln)]
Þ dependencia exponencial
(Gp:) i » IS·e
(Gp:) V
(Gp:) VT
i » -IS
Ecuación característica de una unión PN “larga”
Muy
importante
Þ constante
(corriente inversa de saturación)

Unión de Ge (Ejemplo 1), sin efectos adicionales
(Gp:) P
(Gp:) N
(Gp:) +
(Gp:) –
(Gp:) i
(Gp:) V
Curva característica de una unión PN “larga” a diferentes escalas
(Gp:) 0
(Gp:) 1
(Gp:) 0,25
(Gp:) -0,25
(Gp:) i [mA]
(Gp:) V [Volt.]
(Gp:) (exponencial)
(Gp:) -0,8
(Gp:) -0,5
(Gp:) 0
(Gp:) i [?A]
(Gp:) V [Volt.]
(Gp:) (constante)

(Gp:) i pequeña
(Gp:) Zona P
(Gp:) Zona N
(Gp:) + –
(Gp:) Baja resistividad:
VN » 0
(Gp:) Baja resistividad:
VP » 0
(Gp:) V
(Gp:) VN ¹ 0
(Gp:) VP ¹ 0
(Gp:) i grande
Curva característica de una unión PN con otros efectos reales (I)
Efecto de la resistencia de las zonas “neutras”
(Gp:) 0
(Gp:) 1
(Gp:) -4
(Gp:) 30
(Gp:) i [mA]
(Gp:) V [Volt.]
La tensión de contacto ya no es V0 – V
La tensión de contacto siempre tiene el signo indicado
La tensión V puede ser mayor que V0

Curva característica de una unión PN con otros efectos reales (II)
Habíamos supuesto que no había generación de pares electrón-hueco
La corriente inversa aumenta por efecto de esta generación
Generación en la zona de transición
(Gp:) i
(Gp:) + V –
(Gp:)
Zona P
(Gp:)
Zona N
(Gp:) + –
(Gp:) + –
(Gp:) + –
(Gp:) – +
(Gp:) +
(Gp:) –
(Gp:) -40
(Gp:) 0
(Gp:) -2
(Gp:) i [?A]
(Gp:) V [Volt.]

Curva característica de una unión PN con otros efectos reales (III)
Avalancha primaria
(Gp:) -40
(Gp:) 0
(Gp:) -2
(Gp:) i [?A]
(Gp:) V [Volt.]
(Gp:) i
(Gp:) + V –
(Gp:) P
(Gp:)
N
(Gp:) + –
(Gp:) – +
(Gp:) + –
(Gp:) + –
La corriente aumenta fuertemente si se producen pares electrón-hueco adicionales, o bien por choque o bien por otra causa.
Esto será estudiado después
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –

(Gp:) 30
(Gp:) 0
(Gp:) 5
(Gp:) -20
(Gp:) i [mA]
(Gp:) V [Volt.]
Curva característica de una unión PN en escala de máximos valores de uso
(Gp:) En polarización inversa, la corriente conducida es prácticamente nula
(Gp:) En polarización directa, la caída de tensión es prácticamente nula
Muy
importante

Concepto de diodo ideal (I)
(Gp:) En polarización inversa, la corriente conducida es nula, sea cual sea el valor de la tensión inversa aplicada
(Gp:) En polarización directa, la caída de tensión es nula, sea cual sea el valor de la corriente directa conducida
Nos olvidamos de lo que se ha visto sobre electrónica física
Definimos un nuevo componente ideal de teoría de circuitos
(Gp:) Ánodo
(Gp:) Cátodo
(Gp:) i
(Gp:) V
(Gp:) i
(Gp:) V
(Gp:) +
(Gp:) –
Muy, muy
importante
(Gp:) curva característica

Concepto de diodo ideal (II)
(Gp:) Circuito abierto
(Gp:) Corto circuito
(Gp:) i
(Gp:) V
(Gp:) i
(Gp:) V
(Gp:) i
(Gp:) V
Circuito abierto: la corriente conducida es nula, sea cual sea el valor de la tensión aplicada
Corto circuito: la tensión soportada es nula, sea cual sea el valor de la corriente conducida
Diodo ideal

Comparación entre el diodo ideal y el comportamiento de una unión PN
(Gp:) i
(Gp:) V
Diodo ideal
(Gp:) 30
(Gp:) 0
(Gp:) 5
(Gp:) -20
(Gp:) i [mA]
(Gp:) V [Volt.]
Diodo real
El comportamiento de una unión PN es muy semejante al de un diodo ideal

El diodo semiconductor. Diodo de señal
(Gp:) Ánodo
(Gp:) Cátodo
(Gp:) Ánodo
(Gp:) Cátodo
(Gp:) Oblea de semiconductor
(Gp:) Encapsulado (cristal o resina sintética)
(Gp:) Terminal
(Gp:) Terminal
(Gp:) P
(Gp:) N
(Gp:) Marca señalando el cátodo
(Gp:) Contacto metal-semiconductor
(Gp:) Contacto metal-semiconductor

(Gp:) 1N4007
(Si)
(Gp:) BY251
(Si)
(Gp:) 1N4148
(Si)
(Gp:) OA95
(Ge)
(Gp:) BY229
(Si)
Diodos semiconductores
(Gp:) BYS27-45
(Schottky Si)

Agrupación de diodos semiconductores
(Gp:) 2 diodos en cátodo común
(Gp:) BYT16P-300A
(Si)
(Gp:) +
(Gp:) ~
(Gp:) ~
(Gp:) +
(Gp:) ~
(Gp:) ~
(Gp:) Anillo de diodos
(Gp:) HSMS2827
(Schottky Si)
(Gp:) –
(Gp:) ~
(Gp:) ~
(Gp:) +
(Gp:) Puente de diodos
(Gp:) B380 C1500
(Si)
(Gp:) ~
(Gp:) ~
(Gp:) +
(Gp:) –
(Gp:) B380 C3700
(Si)

Curvas características y circuitos equivalentes
(Gp:) V?
(Gp:) rd
(Gp:) real (asintótico)
(Gp:) ideal
(Gp:) 0
(Gp:) i
(Gp:) V
(Gp:) V?
(Gp:) pendiente = 1/rd
Circuito equivalente asintótico
(Gp:) Curva característica real
(Gp:) Curva característica asintótica
(Gp:) Curva característica ideal
Muy
importante
V? = Tensión de codo
rd = resistencia dinámica

(Gp:)
(Gp:) Decrece con T
(Gp:)
(Gp:) Crece con T
Polarización directa: i » IS·eq·V/(kT)
Polarización inversa: i » -IS
La corriente IS depende fuertemente de la temperatura (aproximadamente se dobla cada 10ºC)
La corriente i aumenta con T (prevalece la tendencia de IS)
siendo: IS = A·q·ni2·[Dp/(ND·Lp)+Dn/(NA·Ln)]
ni depende mucho de la temperatura. Por tanto:
Efectos térmicos sobre la unión (I)

Efectos térmicos sobre la unión (II)
(Gp:) 30
(Gp:) 0,3
(Gp:) 0
(Gp:) i [mA]
(Gp:) V [Volt.]
(Gp:) Polarización directa
(Gp:) P
(Gp:) N
(Gp:) +
(Gp:) –
(Gp:) i
(Gp:) V
(Gp:) 37ºC
(Gp:) 27ºC
(Gp:) -0,25
(Gp:) -2
(Gp:) V [Volt.]
(Gp:) i [?A]
(Gp:) Polarización inversa
En ambos caso, para la misma tensión, la corriente aumenta con la temperatura
Muy
importante
(Gp:) 27ºC
(Gp:) 37ºC

(Gp:) Datos del Si a 300 K
(Gp:) Dp=12,5 cm2/s
Dn=35 cm2/s
?p=480 cm2/V·s
?n=1350 cm2/V·s
ni=1010 port/cm3
?r=11,8
V0=0,596 V
(Gp:) NA=1015 atm/cm3
?p=100 ns
Lp=0,01 mm
(Gp:) ND=1015 atm/cm3
?n=100 ns
Ln=0,02 mm
(Gp:) Zona P Zona N
(Gp:) Dp=50 cm2/s Dn=100 cm2/s ni=2,5·1013 port/cm3
?p=1900 cm2/V·s ?n=3900 cm2/V·s ?r=16
Lp=0,22 mm Ln=0,32 mm ?p= ?n= 10 ?s
NA=1016 atm/cm3 ND=1016 átm/cm2 V0=0,31 V
(Gp:) Datos del Ejemplo 1 (Ge)
Ejemplo 2: unión de Silicio

(Gp:) pP
(Gp:) pNV
(Gp:) nN
(Gp:) nPV
(Gp:) 1010
(Gp:) 1012
(Gp:) 1014
(Gp:) 1016
(Gp:) Portad./cm3
(Gp:) -3
(Gp:) -2
(Gp:) -1
(Gp:) 0
(Gp:) 1
(Gp:) 2
(Gp:) 3
(Gp:) Longitud [mm]
Ejemplo 2 (Si) con V = 0,48 (i = 544?A)
Ejemplo 1 (Ge) con V = 0,18 (i = 566?A)
(Gp:) pNV
(Gp:) pP
(Gp:) nPV
(Gp:) nN
(Gp:) Portad./cm3
(Gp:) 104
(Gp:) 1012
(Gp:) 1014
(Gp:) 1016
(Gp:) -0.3
(Gp:) -0.2
(Gp:) -0.1
(Gp:) 0
(Gp:) 0.1
(Gp:) 0.2
(Gp:) 0.3
(Gp:) Longitud [mm]
(Gp:) 1010
(Gp:) 108
(Gp:) 106
Comparación entre uniones de Silicio y Germanio
¡Ojo con las escalas!
En la unión de Si hace falta más tensión externa para conseguir la misma corriente (aproximadamente)

(Gp:) 0
(Gp:) 1
(Gp:) -4
(Gp:) 30
(Gp:) i [mA]
(Gp:) V [Volt.]
(Gp:) Ge
(Gp:) Si
(Gp:) V [Volt.]
(Gp:) 0
(Gp:) 1
(Gp:) 0,25
(Gp:) – 0,25
(Gp:) i [mA]
(Gp:) 0,5
(Gp:) P
(Gp:) N
(Gp:) +
(Gp:) –
(Gp:) i
(Gp:) V
Comparación Ge/Si: curvas características
(Gp:) Ge
(Gp:) Si
(Gp:) -0,8
(Gp:) -0,5
(Gp:) 0
(Gp:) i [?A]
(Gp:) V [Volt.]
(Gp:) -10
(Gp:) -0,5
(Gp:) 0
(Gp:) i [pA]
(Gp:) V [Volt.]
(Gp:) Ge
(Gp:) Si
Ge: mejor en conducción
Si: mejor en bloqueo
Muy
importante
¡Ojo con las escalas!
¡Ojo con las escalas!

(Gp:) Al cambiar las condiciones de polarización, ¿cambia al instante la conducción?
No, ya que la conducción está ligada a la concentración de portadores de carga en los bordes externos de la zona de transición y al ancho de la zona de transición, siendo en ambos casos necesario crear, destruir o mover portadores de carga, lo que requiere tiempo
Se caracterizan como:
Capacidades parásitas (aplicaciones lineales)
Tiempos de conmutación (en conmutación)
Efectos dinámicos de las uniones PN

Es la dominante con polarización inversa
(Gp:) x
(Gp:) ?(x)
(Gp:) V
(Gp:) Zona P
(Gp:) VO+V
(Gp:) –
(Gp:) +
(Gp:) Zona N
(Gp:) VO+V+?V
(Gp:) –
(Gp:) +
(Gp:) Zona N
(Gp:) V + ?V
(Gp:) Al producirse ?V, hay que extraer portadores de carga para generar esta carga espacial
Capacidades parásitas: capacidad de transición (I)

(Gp:) –
(Gp:) +
(Gp:) P
(Gp:) N
(Gp:) Con V
Unión PN
(Gp:) Con V
(Gp:) + + +
(Gp:) – – –
(Gp:) + + + + +
(Gp:) – – – – –
(Gp:) Con V + ?V
Condensador
Condensador: nuevas cargas a la misma distancia (C=cte.)
Unión PN: nuevas cargas a distinta distancia (C???cte.)
Capacidades parásitas: capacidad de transición (II)
(Gp:) Con V + ?V
(Gp:) –
(Gp:) +
(Gp:) P
(Gp:) N

Capacidades parásitas: capacidad de transición (III)
Es una función del tipo K·(V0-V)-1/2
Ctrans=dQ/dV=?·A/LZT
(Gp:) LZT =
(Gp:) 2·?·(NA+ND)·(V0-V)
(Gp:) q·NA·ND
(Gp:) Ctrans = A·
(Gp:) 2·(NA+ND)·(V0-V)
(Gp:) ?·q·NA·ND
(Gp:) LZT
(Gp:) -dQ
(Gp:) dQ
Partiendo de :
Se obtiene:
(Gp:) 0
(Gp:) V
(Gp:) Ctrans
Muy
importante

Capacidades parásitas: capacidad de transición (IV)
Muy
importante
Los diodos varicap o varactores son diodos que se utilizan como condensadores variables controlados por tensión
Se basan en la capacidad de transición de una unión PN polarizada inversamente
Se utilizan frecuentemente en electrónica de comunicaciones para realizar moduladores de frecuencia, osciladores controlados por tensión, control automático de sintonía, etc.
(Gp:) Símbolo
(Gp:) Se usa polarizado inversamente

Capacidades parásitas: capacidad de difusión (I)
dominante con polarización directa
(Gp:) Polarización inversa
(Gp:) Polarización directa
En polarización directa, Ctrans crece mucho. Sin embargo, carece de importancia porque aparece otro efecto capacitivo: La capacidad de difusión
Esta capacidad está ligada a la concentración de minoritarios en los bordes externos de la zona de transición
(Gp:) 0
(Gp:) V
(Gp:) Ctrans
 Monografias.com"
Monografias.com"
Página siguiente  |