
Demoduladores de ángulo (FM, FSK y PM)
Idea fundamental:
Obtener la forma de onda de la moduladora (información) de la portadora modulada en ángulo, normalmente convertida a una frecuencia intermedia.
(Gp:) Información (moduladora)
(Gp:) Amplificador de FI (o de RF)
(Gp:) Demodulador
(Gp:) Amplificador de banda base
(Gp:) Portadora modulada

Tipos de modulaciones analógicas de ángulo (I)
Modulación de frecuencia (FM)
(Gp:) Modulación
(Gp:) Demodulación
(Gp:) Moduladora
(Gp:) Portadora sin modular
(Gp:) Portadora modulada en FM

Tipos de modulaciones analógicas de ángulo (II)
Modulación de fase (PM)
(Gp:) Modulación
(Gp:) Demodulación
(Gp:) Moduladora
(Gp:) Portadora sin modular
(Gp:) Portadora modulada en PM

Tipos de modulaciones analógicas de ángulo (III)
(Gp:) PM
(Gp:) Moduladora
(Gp:) FM
Ecuaciones:
Moduladora: xm(wmt)
Portadora: vp(wpt) = VP·coswpt
(Gp:) Modulada FM: vpFM(wmt, wpt) = VP·cos[wpt + Dwp·? xm(wmt)·dt]
(Gp:) t
(Gp:) -¥
Comparación entre FM y PM
Modulada PM: vpPM(wmt, wpt) = VP·cos[wpt + Dfp·xm(wmt)]
Si llamamos fp = wp/(2p) y fm max, Dfp max y Dfp max a los máximos valores de fm = wm/(2p), Dfp = Dwp/(2p) y Dfp, respectivamente, se cumple:
DBFM » 2(Dfp max + fm max)
DBPM » 2(Dfp max·fm max + fm max)
FM de banda ancha (radiodifusión): Dfp max = 75 kHz fm max = 15 kHz DB » 180 kHz
FM de banda estrecha (comunicaciones de voz): Dfp max = 5 kHz fm max = 3 kHz DB » 16 kHz

Discriminadores
Detector de cuadratura
Demoduladores con PLLs
Tipos de demoduladores de FM
Esquema general de un discriminadores
(Gp:) Portadora modulada
(Gp:) Limitador
(Gp:) f
(Gp:) v
(Gp:) ve
(Gp:) vs
(Gp:) Convertidor f/v (derivador)
(Gp:) Detector de pico
(Gp:) Moduladora

Ejemplos de circuitos limitadores
(Gp:) Etapa diferencial
(Gp:) 3 etapas con margen dinámico muy pequeño
(Gp:) Con diodos

Ejemplos de convertidores frecuencia/tensión para discriminadores. Con un circuito resonante
(Gp:) R
(Gp:) +
(Gp:) ve
(Gp:) L
(Gp:) R
(Gp:) C
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) vdFM
(Gp:) R’
(Gp:) C’
(Gp:) D
Simple
Poco simétrico
Difícil de ajustar
(Gp:) fo
(Gp:) 1,4·fo
(Gp:) 0,6·fo
(Gp:) 0
(Gp:) ½vs/ve½
(Gp:) 0,5
(Gp:) fFI
(Gp:) Q=5
vdFM =½ vs1½

Ejemplos de convertidores frecuencia/tensión para discriminadores. Con dos circuitos resonantes (I)
Más simétrico
Muy difícil de ajustar
Salida diferencial
(Gp:) 0
(Gp:) ½vs1/ve½
(Gp:) -½vs2/ve½
(Gp:) ½vsFM/ve½
(Gp:) fFI
(Gp:) R
(Gp:) +
(Gp:) ve
(Gp:) L1
(Gp:) C1
(Gp:) vs1
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) R
(Gp:) ve
(Gp:) L2
(Gp:) R
(Gp:) C2
(Gp:) vs2
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) +
(Gp:) vdFM
(Gp:) +
(Gp:) –
(Gp:) ½vs1½
(Gp:) ½vs2½
vdFM =½vs1½- ½vs2½

Ejemplos de convertidores frecuencia/tensión para discriminadores. Con dos circuitos resonantes (II)
Más simétrico
Muy difícil de ajustar
Menor ganancia
(Gp:) R
(Gp:) +
(Gp:) ve
(Gp:) L1
(Gp:) C1
(Gp:) vs1
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) R
(Gp:) ve
(Gp:) L2
(Gp:) R
(Gp:) C2
(Gp:) vs2
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) +
(Gp:) vdFM
(Gp:) +
(Gp:) –
(Gp:) ½vs1½
(Gp:) -½vs2½
(Gp:) R’’
(Gp:) R’’
(Gp:) ½ vs1½- ½ vs2½
(Gp:) 2
(Gp:) vdFM =
Sin salida diferencial

El discriminador de Foster-Seely (I)
Se puede demostrar que:
vs/ve = k1/(1 – LeqCeqw2 + jwLeq/Req)
Siendo:
Leq = Ld2 + Lm·Ld1/(Lm + Ld1)
k1 = Lm/(Lm + Ld1)
Ceq = 4C, Req = R/4
Esquema básico
(Gp:) C
(Gp:) vs1
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vs2
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vdFM
(Gp:) +
(Gp:) –
(Gp:) ½vs1½
(Gp:) ½vs2½
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) ve
(Gp:) +
(Gp:) –
(Gp:) Acoplamiento no ideal
(Gp:) R
(Gp:) 1:1:1

El discriminador de Foster-Seely (II)
Como vs/ve = k1/(1 – LeqCeqw2 + jwLeq/Req), si w = wr = 1/(LeqCeq)1/2, entonces vs/ve = k1Req/(jwrLeq), es decir, vs y ve están desfasados 90º
El circuito se diseña para wr = wp (en la práctica wr = wFI)
También se cumple que vdFM =½vs1½- ½vs2½= ½ve + vs½- ½ve – vs½
(Gp:) C
(Gp:) vs1
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vs2
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vdFM
(Gp:) +
(Gp:) –
(Gp:) ½vs1½
(Gp:) ½vs2½
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) ve
(Gp:) +
(Gp:) –
(Gp:) Acoplamiento no ideal
(Gp:) R
(Gp:) 1:1:1

(Gp:) Si w < wr
(Gp:) Si w > wr
(Gp:) Si w = wr
El discriminador de Foster-Seely (III)
vdFM =½vs1½- ½vs2½= ½ve + vs½- ½ve – vs½
(Gp:) ve
(Gp:) -vs
(Gp:) vs2
(Gp:) ve
(Gp:) vs
(Gp:) vs1
½vs1½½vs2½? vdFM > 0
(Gp:) ve
(Gp:) vs
(Gp:) vs1
(Gp:) -vs
(Gp:) ve
(Gp:) vs2
½vs1½=½vs2½? vdFM = 0
(Gp:) 10,7 MHz
(Gp:) 10,5
(Gp:) 10,9
(Gp:) 0
(Gp:) vdFM
Relación muy lineal vdFM/f
(Gp:) ½vs/ve½

El discriminador de Foster-Seely (IV)
(Gp:) C
(Gp:) vs1
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vs2
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vdFM
(Gp:) +
(Gp:) –
(Gp:) ½vs1½
(Gp:) ½vs2½
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) ve
(Gp:) +
(Gp:) –
(Gp:) Acoplamiento no ideal
(Gp:) R
(Gp:) 1:1:1
(Gp:) C
(Gp:) vs1
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vs2
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vdFM
(Gp:) +
(Gp:) –
(Gp:) ½vs1½
(Gp:) ½vs2½
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) ve
(Gp:) +
(Gp:) –
(Gp:) Acoplamiento no ideal
(Gp:) R
(Gp:) 1:1:1
(Gp:) Cac
(Gp:) Lch
Salida diferencial
Salida referida a masa

El discriminador de relación (I)
(Gp:) C
(Gp:) vs1
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vs2
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vdFM
(Gp:) +
(Gp:) –
(Gp:) ½vs1½
(Gp:) ½vs2½
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) ve
(Gp:) +
(Gp:) –
(Gp:) Acoplamiento no ideal
(Gp:) R
(Gp:) 1:1:1
(Gp:) Foster-Seely
(Gp:) Relación
(Gp:) -½vs2½
(Gp:) C
(Gp:) vs1
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vs2
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vdFM
(Gp:) +
(Gp:) –
(Gp:) ½vs1½
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) ve
(Gp:) +
(Gp:) –
(Gp:) Acoplamiento no ideal
(Gp:) R
(Gp:) 1:1:1
(Gp:) R’’
(Gp:) R’’
vdFM =½vs1½- ½vs2½
(Gp:) ½ vs1½- ½ vs2½
(Gp:) 2
(Gp:) vdFM =

El discriminador de relación (II)
(Gp:) -½vs2½
(Gp:) C
(Gp:) vs1
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vs2
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vdFM
(Gp:) +
(Gp:) –
(Gp:) ½vs1½
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) ve
(Gp:) +
(Gp:) –
(Gp:) Acoplamiento no ideal
(Gp:) R
(Gp:) 1:1:1
(Gp:) R’’
(Gp:) R’’
(Gp:) vs12
(Gp:) +
(Gp:) –
(Gp:) 0
(Gp:) vdFM
(Gp:) 10,7 MHz
(Gp:) 10,5
(Gp:) 10,9
(Gp:) Foster
(Gp:) Relación
(Gp:) Menor ganancia que en el Foster
(Gp:) 10,7 MHz
(Gp:) 10,5
(Gp:) 10,9
(Gp:) vs12
(Gp:) 0
(Gp:) Vs12 casi costante. Se puede usar para limitar las amplitudes

El discriminador de relación (III)
(Gp:) -½vs2½
(Gp:) C
(Gp:) vs1
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vs2
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vdFM
(Gp:) +
(Gp:) –
(Gp:) ½vs1½
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) ve
(Gp:) +
(Gp:) –
(Gp:) Acoplamiento no ideal
(Gp:) R
(Gp:) 1:1:1
(Gp:) R’’
(Gp:) R’’
Discriminador de relación con limitador de amplitud
(Gp:) C’’
(Gp:) vs12
(Gp:) +
(Gp:) –
(Gp:) -½vs2½
(Gp:) C
(Gp:) vs1
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vs2
(Gp:) +
(Gp:) –
(Gp:) +
(Gp:) –
(Gp:) R’
(Gp:) C’
(Gp:) D
(Gp:) vdFM
(Gp:) +
(Gp:) –
(Gp:) ½vs1½
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) vs
(Gp:) +
(Gp:) –
(Gp:) ve
(Gp:) +
(Gp:) –
(Gp:) R
(Gp:) 1:1
(Gp:) ve
(Gp:) +
(Gp:) –
(Gp:) 1:1
(Gp:) vs12
(Gp:) +
(Gp:) –
(Gp:) C’’
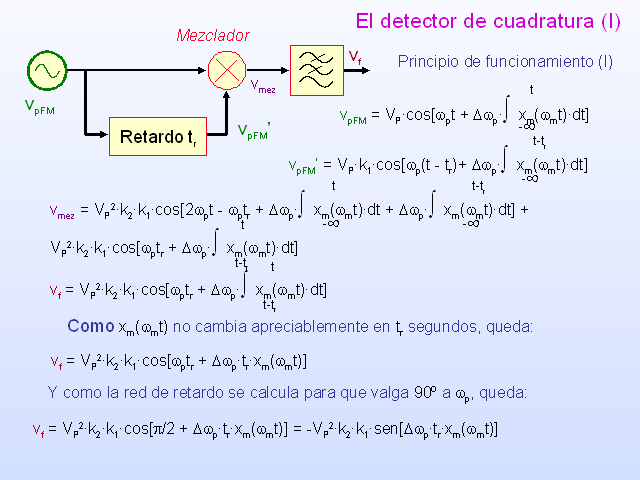
El detector de cuadratura (I)
Principio de funcionamiento (I)
(Gp:) vpFM = VP·cos[wpt + Dwp·? xm(wmt)·dt]
(Gp:) t
(Gp:) -¥
(Gp:) Mezclador
(Gp:) vf
(Gp:) vmez
(Gp:) Retardo tr
(Gp:) vpFM
(Gp:) vpFM’
(Gp:) vpFM’ = VP·k1·cos[wp(t – tr)+ Dwp·? xm(wmt)·dt]
(Gp:) t-tr
(Gp:) -¥
(Gp:) vmez = VP2·k2·k1·cos[2wpt – wptr + Dwp·? xm(wmt)·dt + Dwp·? xm(wmt)·dt] + VP2·k2·k1·cos[wptr + Dwp·? xm(wmt)·dt]
(Gp:) t
(Gp:) -¥
(Gp:) t-tr
(Gp:) -¥
(Gp:) t
(Gp:) t-tr
(Gp:) vf = VP2·k2·k1·cos[wptr + Dwp·? xm(wmt)·dt]
(Gp:) t
(Gp:) t-tr
Como xm(wmt) no cambia apreciablemente en tr segundos, queda:
vf = VP2·k2·k1·cos[wptr + Dwp·tr·xm(wmt)]
Y como la red de retardo se calcula para que valga 90º a wp, queda:
vf = VP2·k2·k1·cos[p/2 + Dwp·tr·xm(wmt)] = -VP2·k2·k1·sen[Dwp·tr·xm(wmt)]
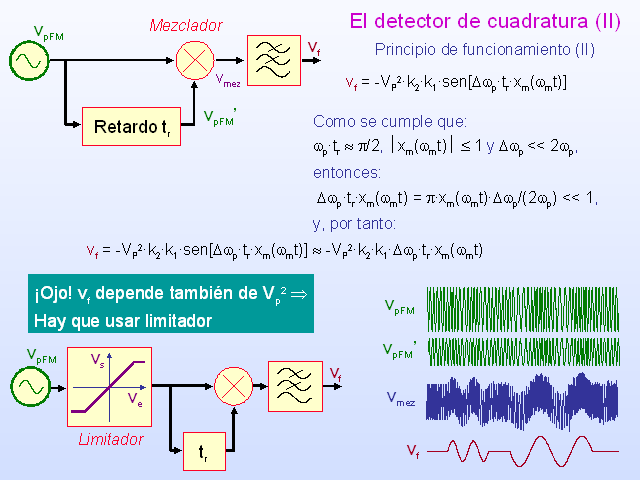
El detector de cuadratura (II)
(Gp:) Mezclador
(Gp:) vf
(Gp:) vmez
(Gp:) Retardo tr
(Gp:) vpFM
(Gp:) vpFM’
Como se cumple que:
wp·tr » p/2, ½xm(wmt)½ £ 1 y Dwp > wm max

Demoduladores de PM con PLLs
(Gp:) vdPM
Principio de funcionamiento
Condición de diseño: el PLL debe ser suficientemente lento para ser insensible a las variaciones de frecuencia Þ
frecuencia de corte del PLL