
COMPONENTES MAGNÉTICOS
¿Por qué un tema dedicado a los componentes magnéticos?
Realizan dos funciones importantísimas en la conversión de la energía eléctrica:
– Transferencia directa de energía eléctrica con posible cambio de escalas de tensión y corriente y obtención de aislamiento galvánico entre entrada y salida Þ transformadores
– Almacenamiento de la energía eléctrica en forma de energía en un campo magnético para su posterior transferencia Þ bobinas (con uno o varios devanados)
Frecuentemente deben diseñarse a medida
En potencias pequeñas, sí se encuentran componentes “estandarizados”

COMPONENTES MAGNÉTICOS
Partes de un componente magnético
(Gp:) Núcleo de material magnético (ferrita, polvo de hierro, aleaciones férricas amorfas, Fe, Fe Si, etc.)
(Gp:) Soporte para albergar el devanado (carrete, “bobbin”)
(Gp:) Devanado o devanados (de hilo de cobre con barniz aislante, pletinas o cintas de cobre, pistas de circuito impreso, etc.)

COMPONENTES MAGNÉTICOS
Partes de un componente magnético
Montaje :
– Se parte del carrete
– Se devanan los devanados o bobinados
– Se introducen los núcleos magnéticos
– Se sujeta todo el conjunto

COMPONENTES MAGNÉTICOS
Partes de un componente magnético
Puede haber una zona en la que el circuito magnético esté interrumpido. Es el entrehierro (“gap”)
Sin entrehierro
Con entrehierro

COMPONENTES MAGNÉTICOS
Partes de un componente magnético
Distintos tipos de entrehierros
(Gp:) Con núcleos estándar
(Gp:) Con núcleos a medida

COMPONENTES MAGNÉTICOS
Tipos de núcleos magnéticos: núcleos compuestos de dos partes
Núcleos en “E”
(Gp:) E
(Gp:) E plano
(Gp:) EFD
Todos estos son de columnas de base rectangular (en algunos casos redondeadas)

COMPONENTES MAGNÉTICOS
Tipos de núcleos magnéticos: núcleos compuestos de dos partes
Núcleos en “E”
Son núcleos de columna central de base circular
(Gp:) EC
(Gp:) ETD

COMPONENTES MAGNÉTICOS
Tipos de núcleos magnéticos: núcleos compuestos de dos partes
Núcleos en “E”
Todos estos también son de columna central de base circular, pero más blindados
(Gp:) EQ
(Gp:) ER
(Gp:) EP

COMPONENTES MAGNÉTICOS
Tipos de núcleos magnéticos: núcleos compuestos de dos partes
Núcleos muy blindados tipo P (“potcores”)
(Gp:) PT
(Gp:) PQ

COMPONENTES MAGNÉTICOS
Tipos de núcleos magnéticos: núcleos compuestos de dos partes
Núcleos muy blindados tipo RM
(Gp:) RM/I
(Gp:) RM
(Gp:) RM/ILP

COMPONENTES MAGNÉTICOS
Tipos de núcleos magnéticos: núcleos compuestos de dos partes
Núcleos muy poco blindados
(Gp:) U
(Gp:) En marco y barra
Núcleos en U:
– Con separación de los devanados
– Muy interesante para alta tensión

COMPONENTES MAGNÉTICOS
Tipos de núcleos magnéticos: núcleos compuestos de una parte
En electrónica de potencia normalmente son toroides

(Gp:) lm
COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
En el estudio de la teoría básica de los componentes magnéticos, vamos a suponer que el núcleo es toroidal
(Gp:) Una de las Ecuaciones de Maxwell
(Gp:) Particularización al componente magnético
(Gp:) S
(Gp:) n
(Gp:) i
Ley de Ampère

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
(Gp:) Ahora ya partimos de:
Suponemos que el campo magnético fuera del núcleo es despreciable y que tiene el mismo módulo en todo él (sección uniforme), de tal forma que:
(Gp:) (lm es la longitud media del toroide)
(Gp:) Por tanto:
(Gp:) n
(Gp:) i
(Gp:) Llamamos “Fuerza magnetomotriz” (Fmm) a ni:
(Gp:) lm
(Gp:) n
(Gp:) i
Ley de Ampère para un toroide de sección uniforme y sin entrehierro
COMPONENTES MAGNÉTICOS
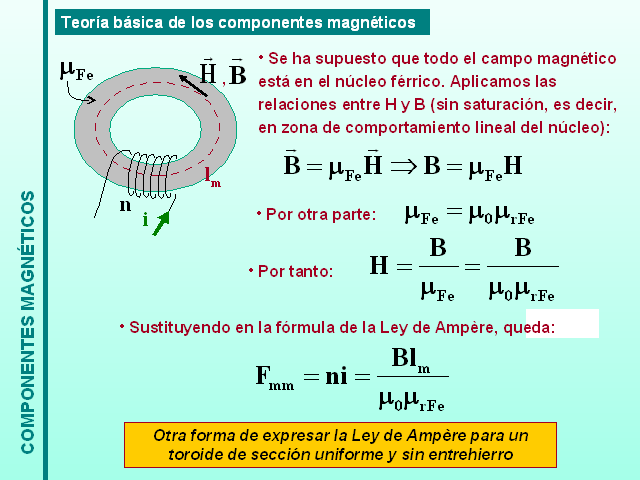
Teoría básica de los componentes magnéticos
Se ha supuesto que todo el campo magnético está en el núcleo férrico. Aplicamos las relaciones entre H y B (sin saturación, es decir, en zona de comportamiento lineal del núcleo):
(Gp:) Por otra parte:
(Gp:) Sustituyendo en la fórmula de la Ley de Ampère, queda:
(Gp:) Por tanto:
(Gp:) lm
(Gp:) n
(Gp:) i
Otra forma de expresar la Ley de Ampère para un toroide de sección uniforme y sin entrehierro
(Gp:) ,

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Por otra parte, definimos el flujo magnético f como:
(Gp:) Sustituyendo de nuevo en la en la fórmula de la Ley de Ampère, queda:
Otra forma más de escribir la Ley de Ampère para un toroide con sección uniforme y sin entrehierro
(Gp:) lm
(Gp:) n
(Gp:) i
(Gp:) A

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Esta es la Ley de Ampère aplicada a un núcleo de sección uniforme y sin entrehierro. ¿Cómo sería la Ley de Ampère si hubiera entrehierro?
Para estudiar este caso, hace falta recordar el comportamiento del campo magnético en un cambio de medio
La densidad de flujo es la misma en ambos medios
La intensidad de campo magnético cambia con el medio
(Gp:) lm
(Gp:) n
(Gp:) i
(Gp:) A
COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
(Gp:) n
(Gp:) i
(Gp:) »lm
(Gp:) g
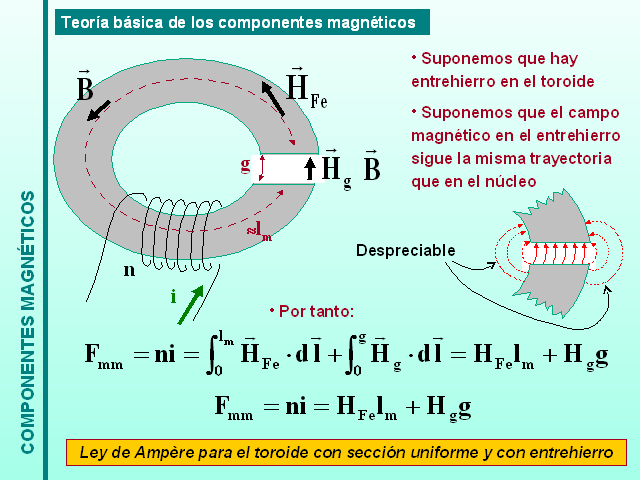
Suponemos que hay entrehierro en el toroide
Suponemos que el campo magnético en el entrehierro sigue la misma trayectoria que en el núcleo
Ley de Ampère para el toroide con sección uniforme y con entrehierro
(Gp:) Por tanto:
(Gp:) Despreciable

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
(Gp:) n
(Gp:) i
(Gp:) »lm
(Gp:) g
Aplicamos las relaciones entre H y B (sin saturación, es decir, en zona de comportamiento lineal del núcleo):
(Gp:) Por otra parte:
(Gp:) y
(Gp:) Sustituyendo en la fórmula de la Ley de Ampère, queda:
(Gp:) Por tanto:
(Gp:) y

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
(Gp:) n
(Gp:) i
(Gp:) »lm
(Gp:) g
(Gp:) entonces la Ley de Ampère queda:
(Gp:) A
(Gp:) Como:
Otra forma de escribir la Ley de Ampère para un toroide con sección uniforme y con entrehierro
Esta es la Ley de Ampère aplicada a un núcleo de sección uniforme. ¿Cómo sería la Ley de Ampère si la sección no fuera uniforme?
Para estudiar este caso, hace falta recordar una de las propiedades básicas de los campos magnéticos: son campos de divergencia nula (adivergentes)

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Forma integral de la condición de divergencia nula (el flujo neto que atraviesa una superficie cerrada es nulo) :
Como sólo hay flujo distinto de cero en A1 y A2, la condición anterior se puede escribir como:
(Gp:) Por tanto:
(Gp:) A2
(Gp:) A1
(Gp:) y
El flujo es el mismo en todas las secciones

(Gp:) n
(Gp:) i
COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
(Gp:) g
(Gp:) A1
Toroide con zonas de distinto área y con entrehierro
(Gp:) A2
(Gp:) l1a
(Gp:) l1b
(Gp:) l2
(Gp:) mrFe
(Gp:) f
(Gp:) Aplicando la Ley de Ampère queda:

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
(Gp:) n
(Gp:) i
(Gp:) g
(Gp:) A1
(Gp:) A2
(Gp:) l1a
(Gp:) l1b
(Gp:) l2
(Gp:) mrFe
(Gp:) f
(Gp:) Reluctancia de la zona de sección A1 en el material férrico:
(Gp:) Reluctancia de la zona de sección A2 en el material férrico:
(Gp:) Reluctancia del entrehierro (de sección A1):
Ley de Ampère para un toroide

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
(Gp:) n
(Gp:) i
(Gp:) g
(Gp:) A1
(Gp:) A2
(Gp:) l1a
(Gp:) l1b
(Gp:) l2
(Gp:) mrFe
(Gp:) f
Equivalencia magnética-eléctrica
Ley de Ampère para un componente de un único circuito magnético
(Gp:) VEE
(Gp:) R1
(Gp:) R2
(Gp:) R3
(Gp:) iEE
Ley de Ohm para un circuito de una única malla

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
(Gp:) n
(Gp:) i
(Gp:) g
(Gp:) A1
(Gp:) A2
(Gp:) l1a
(Gp:) l1b
(Gp:) l2
(Gp:) mrFe
(Gp:) f
Equivalencia magnética-eléctrica
(Gp:) VEE
(Gp:) R1
(Gp:) R2
(Gp:) R3
(Gp:) iEE
Fuerza magnetomotriz
Flujo magnético
Reluctancia
Permeabilidad absoluta
Fuerza electromotriz (tensión)
Corriente eléctrica
Resistencia
Conductividad
Þ
Þ
Þ
Þ

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Equivalencia magnética-eléctrica en circuitos con varias ramas
f1=B1A1
f2=B2A2
f3=B3A3
(Gp:) A2
(Gp:) A3
(Gp:) A1
f1 = f2 + f3
(consecuencia de la adivergencia de B)
(Gp:) i1=j1A1
(Gp:) i2=j2A2
(Gp:) i3=j3A3
(Gp:) A2
(Gp:) A1
(Gp:) A3
i1 = i2 + i3
(Kirchhoff)
También es válida

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Equivalencia magnética-eléctrica en circuitos con varias ramas
(Gp:) g
(Gp:) llat
(Gp:) lc/2
(Gp:) Alat
(Gp:) Ac
(Gp:) llat
(Gp:) lc/2
(Gp:) Rlat
(Gp:) Rlat
(Gp:) Rc
(Gp:) Rg
Þ Rlat
Þ Rg
Þ Rc

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Equivalencia magnética-eléctrica en circuitos con varias ramas
(Gp:) Rlat
(Gp:) Rlat
(Gp:) Rc
(Gp:) Rg
(Gp:) VEE
(Gp:) i
(Gp:) i1
(Gp:) i2
(Gp:) i3
(Gp:) f1
Ejemplo: cálculo de i1
n
COMPONENTES MAGNÉTICOS
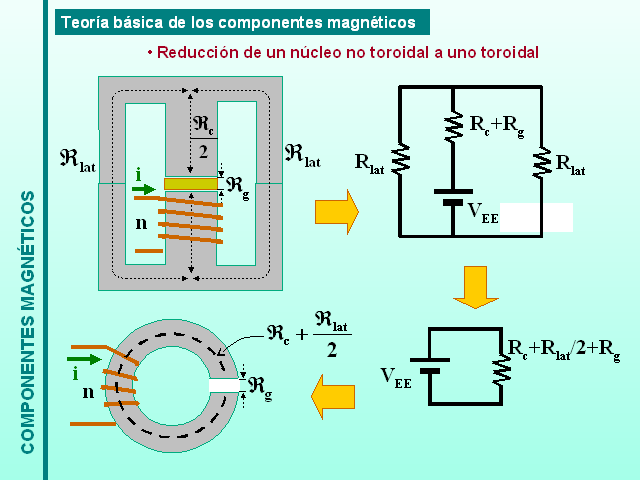
Teoría básica de los componentes magnéticos
Reducción de un núcleo no toroidal a uno toroidal
(Gp:) Rlat
(Gp:) Rlat
(Gp:) Rc+Rg
(Gp:) VEE
(Gp:) Rc+Rlat/2+Rg
(Gp:) VEE
(Gp:) i
(Gp:) n
(Gp:) i
(Gp:) n

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Datos de un fabricante
(Gp:) Ae
(Gp:) le
(Gp:) E30/15/7
Ve » Aele

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Datos de un fabricante
(Gp:) E30/15/7
Valor desde el que se puede calcular la reluctancia total del circuito magnético

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Datos de un fabricante: Introducción de un entrehierro
(Gp:) gn
(Gp:) gn
(Gp:) gn
(Gp:) g
(Gp:) g
(Gp:) g
g = 2gn
g = gn
g = gn
(Gp:) A2
(Gp:) A2
(Gp:) A1
(Gp:) A1 = 2A2

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Concepto de autoinducción (o inductancia)
(Gp:) – Por la Ley de Ampère sabemos que:
(Gp:) – Definimos autoinducción:
(Gp:) – Por tanto:
AL recibe el nombre de permeancia. Muchas veces se representa por P

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Cálculo de la autoinducción con entrehierro desde la permeancia AL sin entrehierro, AL0
(Gp:) – Por tanto:
(Gp:) – Partimos de:
(Gp:) – Como , entonces:
Siendo:
AL0: Permeancia sin entrehierro
n: número de espiras
g: longitud del entrehierro
Ae: Área efectiva de la sección del núcleo
m0: permeabilidad del vacío (4p10-7 Hm-1)

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Relación entre la tensión eléctrica y magnitudes magnéticas
(Gp:) Una de las Ecuaciones de Maxwell
Particularización al componente magnético
Ley de Faraday
(Gp:) +
(Gp:) –
(Gp:) v
(Gp:) ST
(Gp:) Por tanto:
(Gp:) n
(Gp:) f

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Relación entre la tensión eléctrica y corriente eléctrica
(Gp:) – Usando la definimos autoinducción, , obtenemos:
(Gp:) y como i sólo puede cambiar con el tiempo:
(Gp:) +
(Gp:) –
(Gp:) v
(Gp:) L
(Gp:) i
Otra forma de expresar la Ley de Faraday

COMPONENTES MAGNÉTICOS
Teoría básica de los componentes magnéticos
Resumen
(Gp:) g
(Gp:) L
(Gp:) Ae
(Gp:) f
(Gp:) n
(Gp:) +
(Gp:) –
(Gp:) v
(Gp:) i
Los componentes magnéticos se estudian reduciendo el comportamiento de su núcleo al de un toroide equivalente con posible entrehierro
El comportamiento tensión corriente del componente nos lo da la ley de Faraday:
La inductancia L del componente magnético depende del número de espiras al cuadrado y de la reluctancia del núcleo y del entrehierro, según la fórmula:
La densidad de flujo en el núcleo magnético vale:

COMPONENTES MAGNÉTICOS
Diseño de componentes magnéticos
(Gp:) g
(Gp:) L
(Gp:) n
(Gp:) +
(Gp:) –
(Gp:) v
(Gp:) i
Vamos a estudiar tres casos:
(Gp:) L1
(Gp:) n1
(Gp:) +
(Gp:) –
(Gp:) v1
(Gp:) i1
(Gp:) n2
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) i2
(Gp:) L2
(Gp:) L1
(Gp:) n1
(Gp:) +
(Gp:) –
(Gp:) v1
(Gp:) i1
(Gp:) n2
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) i2
(Gp:) L2
(Gp:) g
– Bobinas con un único devanado (almacenar energía eléctrica)
– Transformadores
(cambiar la escala de tensión y corriente y aislamiento galvánico)
– Bobinas con varios devanados (almacenar energía eléctrica, cambiar la escala de tensión y corriente y aislamiento galvánico)

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
(Gp:) g
(Gp:) L
(Gp:) n
(Gp:) +
(Gp:) –
(Gp:) v
(Gp:) i
Datos de partida:
– Valor de la inductancia deseada, L
– Forma de onda de la corriente por la bobina. En particular, valor máximo de la corriente, imax
– Características del núcleo de partida. En particular, de su permeancia sin entrehierro, AL0 y sus dimensiones (Ae y lm)
Datos a obtener:
– Necesidad o no de entrehierro. Si es necesario, su longitud, g
– Número de espiras, n
– Diámetro del conductor del devanado, d
– Verificación de si nos vale núcleo magnético a usar
Diseño no optimizado

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
(Gp:) g
(Gp:) L
(Gp:) n
(Gp:) +
(Gp:) –
(Gp:) v
(Gp:) i
Proceso de cálculo:
– Realizar el cálculo completo con un tamaño determinado de núcleo. Su elección se basa en la experiencia previa del diseñador.
– El cálculo anterior debe incluir la determinación de la longitud del entrehierro, si éste es necesario (caso más habitual)
– Con el número de espiras calculado, estimación de las pérdidas en los devanados en función del grosor del hilo empleado. La sección total de hilo conductor debe caber en el núcleo
– En caso que el diseño no se juzgue adecuado, cambiar de tamaño y/o forma del núcleo
Diseño no optimizado

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
(Gp:) L
(Gp:) n
(Gp:) i
Diseño sin entrehierro (habitualmente no es válido):
– Partimos de un núcleo elegido (AL0 y Ae), de L y de imax
Diseño no optimizado
Normalmente Bmax > Bsat (300-400 mT), por lo que el diseño no es válido
(el valor de AL0 no es el supuesto inicialmente al estar el núcleo saturado y haber perdido, por tanto, sus propiedades magnéticas)

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño con entrehierro:
– Partimos de un núcleo elegido (AL0 y Ae), de L, de imax y de la Bmax deseada, siempre menor que la de saturación
– Calculamos n:
Diseño no optimizado
(Gp:) L
(Gp:) n
(Gp:) i
(Gp:) g
(Gp:) (se debe elegir un número entero, el mayor más próximo)
– Calculamos g:
– Ahora ya conocemos n y g. El siguiente paso es calcular las pérdidas y reconsiderar el diseño

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño no optimizado
Las pérdidas se dividen en:
– Pérdidas en el devanado (vulgarmente, pérdidas en el cobre)
– Pérdidas en el núcleo (vulgarmente, pérdidas en el hierro)
Para calcular las pérdidas en el devanado hace falta:
– Calcular el valor eficaz de la forma de onda de la corriente
– Calcular el valor de la resistencia del devanado
Para calcular la resistencia del devanado hace falta:
– Calcular la longitud del hilo del devanado
– Calcular la sección del hilo del devanado

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño no optimizado
Cálculo de la longitud del hilo del devanado (ejemplo de sección circular):
(Gp:) rm
Cálculo de la sección del hilo del devanado
– Sección total de cobre en la “ventana” del núcleo:
(Gp:) (d es el diámetro del hilo de cobre)
– Sección total de la “ventana” del núcleo: AW
– Como el hilo de cobre no se ajusta perfectamente en la ventana, hay parte del área que no es posible llenar y queda vacía. Se define el “factor de ventana” fW:
(Gp:) (típicamente fW » 0,3)
(Gp:) AW

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño no optimizado
(Gp:) – Como el devanado debe caber en la ventana, se debe cumplir:
– Supongamos que toda la sección de cobre es útil para la circulación de corriente. Entonces la resistencia del devanado vale:
(Gp:) rm
(Gp:) AW
(Gp:) – Pérdidas en el devanado:
Para un núcleo dado, las pérdidas en el devanado crecen con n2

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño no optimizado
¿Es útil de verdad toda la sección de cobre para la circulación de corriente eléctrica? Hay que hablar de los efectos “pelicular” y “proximidad”
– Efecto pelicular: en un conductor aislado que conduce corriente eléctrica con una componente de alterna, el campo magnético variable que ésta genera redistribuye de forma no uniforme la densidad de corriente en el conductor, produciéndose zonas en las que casi no hay conducción de corriente
– Efecto proximidad: como el efecto pelicular, pero en presencia de un campo magnético producido por la conducción de corriente por otros trozos de conductor
(Gp:) Conductor macizo en continua
(Gp:) Conductor macizo único en alterna
(Gp:) Conductor macizo no único en alterna
(Gp:) Múltiples conductores paralelos en alterna

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño no optimizado
Concepto de profundidad pelicular (“skin”) o profundidad de penetración:
(Gp:) ds
A 60 Hz Þ ds= 8,5 mm
A 100 kHz Þ ds= 0,21 mm
A 1 MHz Þ ds= 0,067 mm
(esto ocurriría con sólo alterna; en la mayoría de las bobinas de los convertidores hay una fuerte componente de continua, por lo que la situación no es tan grave)
La mejor manera de aprovechar la sección de cobre es sustituir el conductor macizo por otro compuesto por muchos conductores de diámetro menor de 2ds. Esto encarece el devanado.
El hilo “litz” se basa en este principio
(Gp:) >2ds

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño no optimizado
Pérdidas en el núcleo de un componente magnético
– Por histéresis
La curva B-H real tiene histéresis. El funcionamiento del componente describe un área en la curva B-H que define las pérdidas por histéresis
– Por corrientes inducidas en el núcleo (“eddy currents”)
El flujo magnético variable induce corrientes en el propio núcleo. La circulación de estas corrientes provoca pérdidas
Es importante que el material férrico del núcleo tenga alta resistividad eléctrica
(Gp:) HFe
(Gp:) BFe

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño no optimizado
Cálculo analítico de las pérdidas en el núcleo
– Las pérdidas crecen con la componente de alterna de la densidad de flujo y con la frecuencia. Una fórmula empírica aproximada es:
Siendo:
k: una constante
Ve: volumen efectivo del núcleo
f: frecuencia de la componente alterna
Bp: valor de pico de la componente alterna de la densidad de flujo
x: exponente muy variable
y: exponente de valor próximo a 2
Para un núcleo dado y a una frecuencia fija, las pérdidas en el núcleo decrecen con n2
Siendo:
Ae: área efectiva del núcleo
ip: valor de pico de la componente alterna de la corriente

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño no optimizado
– Los valores de k, x e y se pueden obtener desde curvas de pérdidas suministradas por los fabricantes de núcleos

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño no optimizado
Pérdidas totales:
(Gp:) PFe
(Gp:) PT
(Gp:) PCu
(Gp:) n
(Gp:) Pérdidas
– Ahora ya conocemos las pérdidas totales en la bobina. Si éstas son suficientemente bajas, el diseño es adecuado. En caso contrario habrá que elegir un núcleo mayor.
– Sin embargo, hay otra forma de enfocar el diseño. Se trata de intentar trabajar a mínimas pérdidas, partiendo de elegir n para pérdidas mínimas.
(Gp:) Diseño realizado
(Gp:) Diseño de optimización de pérdidas

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño optimizado
(Gp:) PFe
(Gp:) PT
(Gp:) PCu
(Gp:) n
(Gp:) Pérdidas
– En esta función, el mínimo se alcanza cuando PFe = Pcu. Por tanto:
– Sin embargo, este diseño no garantiza que la densidad de flujo esté por debajo de la de saturación. Por tanto, hay que comprobarlo
(Gp:) nop

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Diseño optimizado
(Gp:) PFe
(Gp:) PT
(Gp:) PCu
(Gp:) n
(Gp:) Pérdidas
(Gp:) nop
– Si Bop < Bsat, entonces el diseño es posible.
(Gp:) – Sabemos que:
– Si Bop > Bsat, entonces el diseño no es posible. Hay que elegir otro núcleo o hacer un diseño no optimizado
(Gp:) B
(Gp:) n
(Gp:) Bsat
(Gp:) nop
(Gp:) Bop
(Gp:) B
(Gp:) n
(Gp:) Bsat
(Gp:) nop
(Gp:) Bop
COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
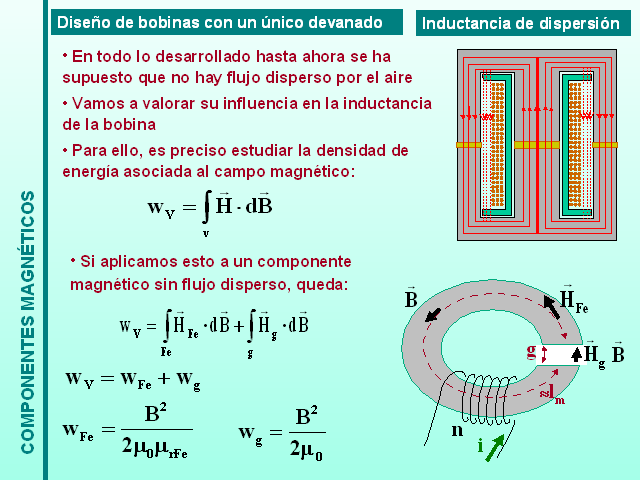
Inductancia de dispersión
En todo lo desarrollado hasta ahora se ha supuesto que no hay flujo disperso por el aire
Vamos a valorar su influencia en la inductancia de la bobina
Para ello, es preciso estudiar la densidad de energía asociada al campo magnético:
(Gp:) n
(Gp:) i
(Gp:) »lm
(Gp:) g
Si aplicamos esto a un componente magnético sin flujo disperso, queda:

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Inductancia de dispersión
Habitualmente, . Ejemplo:
g » 1 mm; lm» 70 mm; mrFe» 2200
La mayor parte de la energía se almacena en el entrehierro
(Gp:) i
(Gp:) n
(Gp:) Baja energía
(Gp:) Alta energía
La energía almacenada vale:

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Inductancia de dispersión
(Gp:) i
(Gp:) n
(Gp:) Baja energía
(Gp:) Alta energía
¿Es esto extraño?
No, es lo mismo que pasa en el equivalente eléctrico
(Gp:) Siendo Rg >>RFe
(Gp:) VEE
(Gp:) RFe
(Gp:) Rg
(Gp:) Baja potencia
(Gp:) Alta potencia
Cuanto más pequeña es la suma de reluctancias, más energía se almacena en el núcleo
Para una suma de reluctancias dada, cuanto mayor es la del entrehierro, más se almacena en él

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Inductancia de dispersión
Analicemos ahora lo que ocurre con el flujo disperso
– Representamos la fuerza magnetomotriz Fmm(x) en la ventana
– Aplicamos la Ley de Ampère a los caminos que describe el flujo disperso:
(Gp:) ni
(Gp:) ni2/3
(Gp:) ni/3
(Gp:) Fmm(x)
(Gp:) x
(Gp:) l1W
– La densidad de energía en la ventana vale:
– Y la energía en el volumen de las ventanas vale:

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Inductancia de dispersión
(Gp:) – Por tanto:
(Gp:) – Por otra parte:
(Gp:) – Por tanto:
siendo Ld la inductancia de dispersión
– En nuestro ejemplo:
(Gp:) ni
(Gp:) ni2/3
(Gp:) ni/3
(Gp:) Fmm(x)
(Gp:) x
(Gp:) l1W
(Gp:) l2W
(Gp:) l2Wa
(Gp:) l3W

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Inductancia de dispersión
Modelo equivalente eléctrico sin dispersión:
(Gp:) VEE
(Gp:) RFe
(Gp:) Rg
Modelo equivalente eléctrico con dispersión:
(Gp:) RFe
(Gp:) VEE
(Gp:) Rg
(Gp:) i1
(Gp:) RW
(Gp:) i2
(Gp:) iT
(Gp:) i1
(Gp:) Por tanto:
(Gp:) Siendo:
(Gp:) Por tanto:

COMPONENTES MAGNÉTICOS
Diseño de bobinas con un único devanado
Inductancia de dispersión
(Gp:) En conclusión, la inductancia total es la suma de la teórica sin dispersión más la de dispersión:
(Gp:) i
(Gp:) L1
(Gp:) Ld
(Gp:) LT
(Gp:) l1W
(Gp:) l2W
(Gp:) l2Wa
(Gp:) l3W
(Gp:) g/2
– En nuestro ejemplo:

(Gp:) +
(Gp:) –
(Gp:) v1
(Gp:) +
COMPONENTES MAGNÉTICOS
Diseño de transformadores
En una primera aproximación, vamos a despreciar el flujo disperso. Analizamos la teoría básica de un transformador
Relaciones entre n1, n2, L1 y L2:
(Gp:) L1
(Gp:) n1
(Gp:) n2
(Gp:) L2
(Gp:) io1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) io2=0
Colocamos una fuente de tensión en un devanado. Ocurren los siguientes fenómenos:
(Gp:) f
– Se produce un flujo magnético f y una corriente io1, de acuerdo con la Ley de Faraday:
– Como el otro devanado está atravesado por el mismo flujo:
(Gp:) – Y como está en vacío:
(Gp:) L1
(Gp:) n1
(Gp:) n2
(Gp:) L2
Sin flujo disperso

COMPONENTES MAGNÉTICOS
Diseño de transformadores
(Gp:) i2
Ahora colocamos una resistencia en la salida de tensión v2. Obligatoriamente circulara una corriente i2:
– Pero, el flujo tiene que estar determinado por la Ley de Faraday. ¿Cómo se compatibilizan ambas “obligaciones”?
(Gp:) +
(Gp:) –
(Gp:) v1
(Gp:) +
(Gp:) i1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) f
(Gp:) L1
(Gp:) n1
(Gp:) n2
(Gp:) L2
Sin flujo disperso
(Gp:) R2
– También obligatoriamente la corriente i2 tiene que generar un flujo f2:

COMPONENTES MAGNÉTICOS
Diseño de transformadores
El flujo total debe ser f. Asimismo, i2 crea un nuevo flujo f2. Obligatoriamente se debe crear otro flujo f1 para cancelar el efecto de f2:
(Gp:) i2
(Gp:) +
(Gp:) –
(Gp:) v1
(Gp:) +
(Gp:) i1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) f
(Gp:) L1
(Gp:) n1
(Gp:) n2
(Gp:) L2
(Gp:) R2
(Gp:) – Y también: . Por tanto:
(Gp:) – Teniendo en cuenta la relación entre L1 y L2, se obtiene:
Sin flujo disperso

COMPONENTES MAGNÉTICOS
Diseño de transformadores
(Gp:) i2
(Gp:) +
(Gp:) –
(Gp:) v1
(Gp:) +
(Gp:) i1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) L1
(Gp:) n1
(Gp:) n2
(Gp:) L2
(Gp:) R2
Sin flujo disperso
(Gp:) io2=0
(Gp:) +
(Gp:) –
(Gp:) v1
(Gp:) +
(Gp:) io1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) L1
(Gp:) n1
(Gp:) n2
(Gp:) L2
Resumen:

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Sin flujo disperso
Representación:
(Gp:) Transformador ideal (ni siquiera magnético)
(Gp:) io1
(Gp:) L1
(Gp:) n1:n2
(Gp:) v1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) +
(Gp:) –
(Gp:) i2
(Gp:) i1
(Gp:) i2n2/n1
(Gp:) R2
(Gp:) +
(Gp:) i2
(Gp:) +
(Gp:) nv1
(Gp:) ni2
(Gp:) v1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) +
(Gp:) –
(Gp:) i1i
(Gp:) i2
(Gp:) i1i
(Gp:) 1:n
(Gp:) v1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) +
(Gp:) –
(Gp:) v2 = v1n i2 = i1i/n

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Sin flujo disperso
Terminología habitual:
(Gp:) i1
(Gp:) i2’
(Gp:) Transformador ideal
(Gp:) im
(Gp:) Lm
(Gp:) n1:n2
(Gp:) v1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) +
(Gp:) –
(Gp:) i2
(Gp:) R2
(Gp:) +
Lm es la inductancia magnetizante. Aquí se ha “referido” al primario del transformador, pero se puede referir al secundario o a cualquier otro devanado (si existe). Interesa que sea lo mayor posible
Lm caracteriza el hecho de que el transformador electromagnético transfiere energía creando y compartiendo flujo magnético
La corriente por Lm es la corriente magnetizante im. En general interesa que sea lo menor posible

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Sin flujo disperso
Procedimiento de diseño:
– Partimos de un núcleo elegido (AL0 y Ae), de v1, del intervalo de tiempo ton = t1 – t0 en el que va a crecer el flujo (tiempo en el que v1 es, por ejemplo, positiva), del valor de B en t0 (es decir, de B0) y del valor máximo deseado de B (es decir, de Bmax), siempre menor que la de saturación
– Calculamos n1 desde la Ley de Faraday:
(Gp:) – Calculamos n2 en función de v2:
– Asignamos a cada devanado la mitad de la ventana. Calculamos la sección de los conductores y las pérdidas como en las bobinas (en el caso de los transformadores, el efecto proximidad es muy importante)
– Si el diseño no nos satisface, se recalcula con otro núcleo. También es posible adaptar el diseño optimizado a los transformadores

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Sin flujo disperso
El transformador tiene como misión transformar, no almacenar, energía eléctrica. Sin embargo, siempre se almacena una parte de energía eléctrica en la inductancia magnetizante
¿Debe colocarse un entrehierro en el circuito magnético de un transformador para que su núcleo férrico no se sature? No, si trabaja como tal
¿Por qué un entrehierro soluciona los problemas de saturación en una bobina y no en un transformador?
(Gp:) Transformador: el la densidad de flujo la fija la tensión:
(Gp:) luego B decrece al crecer n
(Gp:) y
(Gp:) luego B decrece al crecer g
(Gp:) Bobina: la densidad de flujo la fija la corriente y depende de la reluctancia del circuito magnético, que se puede modificar con g:

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Sin flujo disperso
(Gp:) i2
(Gp:) +
(Gp:) –
(Gp:) v1
(Gp:) +
(Gp:) i1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) L1
(Gp:) n1
(Gp:) n2
(Gp:) L2
(Gp:) R2
(Gp:) f
(Gp:) 0
(Gp:) L
(Gp:) Fe
(Gp:) A
(Gp:) 1
(Gp:) =
(Gp:) Â
(Gp:) å
(Gp:) i®f
(Gp:) VEE2®n2i2
(Gp:) VEE1®n1i1
Modelo equivalente eléctrico de las magnitudes magnéticas en el transformador
COMPONENTES MAGNÉTICOS
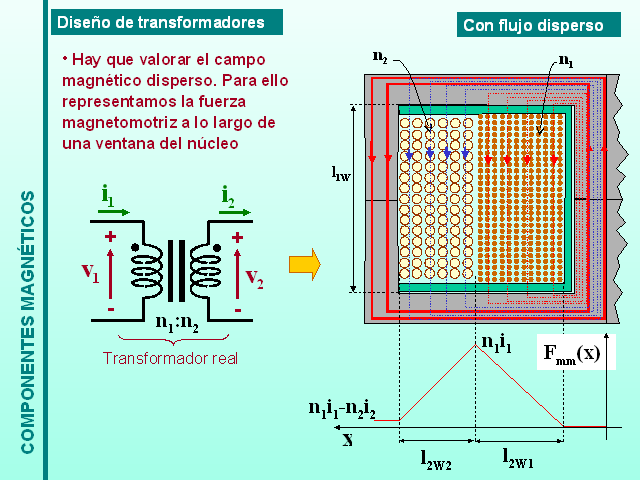
Diseño de transformadores
Con flujo disperso
Hay que valorar el campo magnético disperso. Para ello representamos la fuerza magnetomotriz a lo largo de una ventana del núcleo
(Gp:) l1W
(Gp:) n1i1
(Gp:) n1i1-n2i2
(Gp:) n1
(Gp:) n2
(Gp:) Fmm(x)
(Gp:) x
(Gp:) l2W1
(Gp:) l2W2
(Gp:) i1
(Gp:) Transformador real
(Gp:) n1:n2
(Gp:) v1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) +
(Gp:) –
(Gp:) i2

(Gp:) l3W
COMPONENTES MAGNÉTICOS
Diseño de transformadores
Con flujo disperso
Calculamos la intensidad del campo magnético a lo largo de una ventana del núcleo para después obtener la inductancia de dispersión
(Gp:) n1i1/l1W
(Gp:) x
(Gp:) H(x)
(Gp:) H(x)2
(Gp:) x

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Con flujo disperso
¿Qué se puede hacer para disminuir la inductancia de dispersión? Disminuir los valores de H en la ventana
(Gp:) l1W
(Gp:) Fmm(x)
(Gp:) x
(Gp:) n2/3
(Gp:) 2n1/3
(Gp:) 2n2/3
(Gp:) n1/3
(Gp:) H(x)2
(Gp:) x
(Gp:) n1i1-n2i2
(Gp:) n1i1/3
(Gp:) -n1i1/3
El entrelazado de devanados disminuye la inductancia de dispersión

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Con flujo disperso
(Gp:) n2/3
(Gp:) 2n1/3
(Gp:) 2n2/3
(Gp:) n1/3
(Gp:) Con entrelazado
(Gp:) n2
(Gp:) n1
(Gp:) Sin entrelazado
(Gp:) H(x)2
(Gp:) x
Alta Ld
Baja Ld
(Gp:) x
(Gp:) H(x)2

(Gp:) n2i2
(Gp:) n1i1
COMPONENTES MAGNÉTICOS
Diseño de transformadores
Modelo equivalente eléctrico de las magnitudes magnéticas en el transformador
Con flujo disperso
(Gp:) 2
(Gp:) Fe
(Gp:) Â
(Gp:) VEE2
(Gp:) RFe2
(Gp:) RFe1
(Gp:) RFe1
(Gp:) Rg
(Gp:) RFe3
(Gp:) VEE2
(Gp:) VEE1
(Gp:) VEE1
(Gp:) RFe3
(Gp:) RFe1
(Gp:) RFe1
(Gp:) RFe2
(Gp:) Rg

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Simplificamos el equivalente eléctrico
Con flujo disperso
(Gp:) VEE2
(Gp:) RFe2
(Gp:) RFe1
(Gp:) RFe1
(Gp:) Rg
(Gp:) RFe3
(Gp:) VEE2
(Gp:) VEE1
(Gp:) VEE1
(Gp:) RFe3
(Gp:) RFe1
(Gp:) RFe1
(Gp:) RFe2
(Gp:) Rg
(Gp:) VEE2
(Gp:) RFe2
(Gp:) RFe1
(Gp:) Rg
(Gp:) RFe3
(Gp:) RFe1
(Gp:) VEE1
(Gp:) VEE2
(Gp:) RFe2
(Gp:) 2RFe1+RFe3
(Gp:) Rg
(Gp:) VEE1

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Seguimos simplificamos el equivalente eléctrico
Con flujo disperso
Supongamos que dejamos el devanado secundario en circuito abierto Þ n2i2 = 0 Þ sustituimos la fuente de tensión VEE2 del equivalente eléctrico por un cortocircuito
(Gp:) VEE2
(Gp:) RFe2
(Gp:) 2RFe1+RFe3
(Gp:) Rg
(Gp:) VEE1
(Gp:) VEE2
(Gp:) RFe2
(Gp:) RFe1’
(Gp:) Rg
(Gp:) VEE1
(Gp:) RFe2
(Gp:) RFe1’
(Gp:) Rg
(Gp:) Req1

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Ahora volvemos al circuito magnético
Con flujo disperso
Multiplicamos por n12 tenemos en cuenta la relación entre reluctancias e inductancias:
Siendo:

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Con flujo disperso
Repetimos lo anterior, pero ahora dejando el primario en circuito abierto Þ n1i1 = 0 Þ sustituimos la fuente de tensión VEE1 del equivalente eléctrico por un cortocircuito. Siguiendo idéntico procedimiento, obtenemos:
Siendo:
Por tanto:

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Resumen de lo obtenido
Con flujo disperso
(Gp:) Primario
(Gp:) Secundario
(Gp:) Leq1
(Gp:) Leq2
(Gp:) n1:n2
(Gp:) v1
(Gp:) +
(Gp:) –
(Gp:) v2
(Gp:) +
(Gp:) –
(Gp:) i2
(Gp:) LFe11
(Gp:) LFe21
(Gp:) Ld1
(Gp:) Primario
(Gp:) Secundario
(Gp:) i1
(Gp:) i2n2/n1
(Gp:) Transformador ideal
Modelo en “p”

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Con flujo disperso
(Gp:) n1:n2
(Gp:) LFe1
(Gp:) Ld11
(Gp:) Primario
(Gp:) Secundario
(Gp:) Transformador ideal
(Gp:) Ld21
(Gp:) n2
(Gp:) n1
Con otras estructuras, las inductancias parásitas encajan mejor con un modelo en “T”
Modelo en “T”

COMPONENTES MAGNÉTICOS
Diseño de transformadores
Con flujo disperso
(Gp:) n1:n2
(Gp:) Lm1
(Gp:) Ld1
(Gp:) Primario
(Gp:) Secundario
(Gp:) Transformador ideal
El la práctica, se trabaja con un modelo simplificado de ambos. Se basa en una inductancia de dispersión y en la inductancia magnetizante
La inductancia de dispersión Ld1 se determina midiendo la impedancia del primario con la salida en cortocircuito
La inductancia magnetizante Lm1 se determina midiendo la impedancia del primario con la salida en circuito abierto y restando a esta medición el valor de Ld1

COMPONENTES MAGNÉTICOS
Diseño de bobinas con varios devanados
Realizan las misiones de las bobinas (almacenar energía) y de los transformadores (cambiar la escala tensión-corriente y suministrar aislamiento galvánico)
Para poder realizar correctamente las funciones de una bobina, habitualmente necesitan entrehierro.
Para poder realizar correctamente las funciones de un transformador, el acoplamiento entre devanados debe ser lo mejor posible (baja inductancia de dispersión)
Al contrario que en un transformador, la inductancia magnetizante referida a un devanado debe tener un valor concreto: la inductancia deseada para ese devanado
Las inductancias de todos los devanados están relacionadas entre sí al estar en el mismo núcleo:

COMPONENTES MAGNÉTICOS
Diseño de bobinas con varios devanados
Ejemplo de bobina con dos devanados
(Gp:) Entrehierro
(Gp:) Con entrelazado