1.- Un estudiante reparte propaganda
publicitaria en su tiempo libre. La empresa A le paga
0,05 € por impreso repartido y la empresa B, con
folletos más grandes, le paga 0,07 € por impreso. El
estudiante lleva dos bolsas: una para los impresos de tipo
A, en la que le caben 120, y otra para los de tipo
B, en la que caben 100. Ha calculado que cada día
puede repartir 150 impresos como máximo.
¿Cuántos impresos habrá de repartir de cada
clase para que su beneficio diario sea máximo?

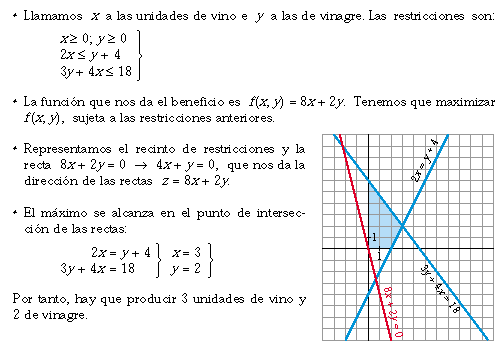
2.- Una industria vinícola produce
vino y vinagre. El doble de la producción de vino es
siempre menor o igual que la producción de vinagre
más cuatro unidades. Además, el triple de la
producción de vinagre más cuatro veces la
producción de vino es siempre menor o igual que 18
unidades. Halla el número de unidades de cada producto que
se deben producir para alcanzar un beneficio máximo,
sabiendo que cada unidad de vino deja un beneficio de 8 € y
cada unidad de vinagre 2 €.
3.- Un autobús Madrid-París
ofrece plazas para fumadores al precio de 100 € y a no
fumadores al precio de 60 €. Al no fumador se le deja llevar
50 kg de peso y al fumador 20 kg. Si el autobús tiene 90
plazas y admite un equipaje de hasta 3 000 kg,
¿cuál debería ser la oferta de la
compañía si se quiere obtener el máximo
beneficio?

4.- Una persona quiere invertir 100 000
€ en dos tipos de acciones, A y B. Las de tipo A tienen
más riesgo, pero producen un beneficio del 10%. Las de
tipo B son más seguras, pero producen solo el 7% nominal.
Decide invertir como máximo 60 000 € en la compra de
acciones A y, por lo menos, 20 000 € en la compra de
acciones B. Además, quiere que lo invertido en A sea, por
lo menos, igual a lo invertido en B. ¿Cómo debe
invertir los 100 000 € para que el beneficio anual sea
máximo?

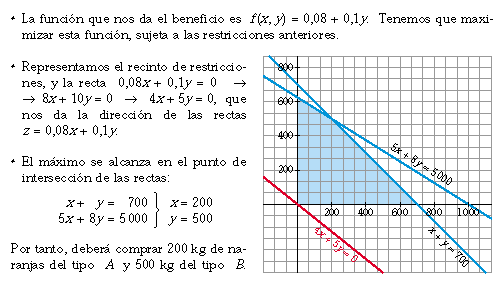
5.- Un comerciante acude a cierto mercado a
comprar naranjas con 500 €. Le ofrecen dos tipos de
naranjas: las de tipo A a 0,5 € el kg y las de tipo B a 0,8
€ el kg. Sabemos que solo dispone en su furgoneta de espacio
para transportar 700 kg de naranjas como máximo y que
piensa vender el kilo de naranjas de tipo A a 0,58 € y el de
tipo B a 0,9 €. ¿Cuántos kilogramos de
naranjas de cada tipo deberá comprar para obtener
beneficio máximo?

6.- Un sastre tiene 80 m2 de tela de
algodón y 120 m2 de tela de lana. Un traje de caballero
requiere 1 m2 de algodón y 3 m2 de lana y un vestido de
señora necesita 2 m2 de cada una de las telas. Calcula el
número de trajes y vestidos que debe confeccionar el
sastre para maximizar los beneficios si un traje y un vestido se
venden por el mismo precio.

7.- Se quiere promocionar una marca
desconocida, D, de aceites, utilizando una marca conocida, C.
Para ello, se hace la siguiente oferta: "Pague a solo 2,5 €
el litro de aceite C y a 1,25 € el litro de aceite D siempre
y cuando compre en total 6 litros o más y la cantidad de
aceite C esté comprendida entre la mitad y el doble de la
cantidad comprada de aceite D". Disponemos de un máximo de
31,25 €.
a) Representa gráficamente los modos
existentes de acogernos a la oferta.
b) Acogiéndonos a la oferta,
¿cuál es la mínima cantidad de aceite D que
podemos comprar? ¿Cuál es la máxima de
C?

8.- Se quiere elaborar una dieta para
ganado que satisfaga unas condiciones mínimas de
contenidos vitamínicos al día: 2 mg de vitamina A,
3 mg de vitamina B, 30 mg de la C y 2 mg de la D.
Para ello, se van a mezclar piensos de dos
tipos, P y Q, cuyo precio por kilo es, para ambos, de 0,3 €
y cuyo contenido vitamínico en miligramos por kilo es el
siguiente:

¿Cómo deben mezclarse los
piensos para que el gasto sea mínimo?

9.- Un pastelero fabrica dos tipos de
tartas T1 y T2, para lo que usa tres ingredientes, A, B y C.
Dispone de 150 kg de A, 90 kg de B y 150 kg de C. Para fabricar
una tarta T1 debe mezclar 1 kg de A, 1 kg de B y 2 kg de C,
mientras que para hacer una tarta T2 necesita 5 kg de A, 2 kg de
B y 1 kg de C.
a) Si se venden las tartas T1 a 10 €,
y las tartas T2 a 23 €, ¿qué cantidad debe
fabricar de cada clase para maximizar sus ingresos?
b) Si se fija el precio de una tarta del
tipo T1 en 15 €, ¿cuál será el precio
de una tarta del tipo T2 si una solución óptima es
fabricar 60 tartas del tipo T1 y 15 del tipo T2?


10.- Una fábrica produce chaquetas y
pantalones. Tres máquinas —de cortar, coser y
teñir— se emplean en la producción. Fabricar
una chaqueta representa usar la máquina de cortar una
hora, la de coser, tres horas y la de teñir, una hora.
Fabricar unos pantalones representa usar la máquina de
cortar una hora, la de coser, una hora y la de teñir,
ninguna hora. La máquina de teñir se puede usar
durante tres horas, la de coser, doce y la de cortar, siete. Todo
lo que se fabrica es vendido y se obtiene un beneficio de ocho
euros por cada chaqueta y cinco por cada pantalón.
¿Cómo emplearemos las máquinas para
conseguir el beneficio máximo?

11.- Un ganadero debe suministrar un
mínimo diario de 4 mg de vitamina A y 6 mg de vitamina B
en el pienso que da a sus reses. Dispone para ello de dos tipos
de pienso P1 y P2, cuyos contenidos vitamínicos por kg son
los que aparecen en la tabla:

Si el kilogramo de pienso P1 vale 0,4
€ y el del P2 0,6 €, ¿cómo deben
mezclarse los piensos para suministrar las vitaminas requeridas
con un coste mínimo?


12.- Se va a organizar una planta de un
taller de automóviles donde van a trabajar electricistas y
mecánicos. Por necesidades de mercado, es necesario que
haya mayor o igual número de mecánicos que de
electricistas y del número de mecánicos no supere
al doble que el de electricistas. En total hay disponibles 30
electricistas y 20 mecánicos. El beneficio de la empresa
por jornada es de 150 € por electricista y 120 € por
mecánico. ¿Cuántos trabajadores de cada
clase deben elegirse para obtener el máximo
beneficio?


13.- Una confitería es famosa por
sus dos especialidades en tartas: la tarta Imperial y la tarta de
Lima. La tarta Imperial requiere para su elaboración medio
kilo de azúcar y 8 huevos y tiene un precio de venta de 8
€. La tarta de Lima necesita 1 kilo de azúcar y 8
huevos, y tiene un precio de venta de 10 €. En el
almacén les quedan 10 kilos de azúcar y 120
huevos.
a) ¿Qué combinaciones de
especialidades pueden hacer? Plantea el problema y representa
gráficamente el conjunto de soluciones.
b) ¿Cuántas unidades de cada
especialidad han de producirse para obtener el mayor ingreso por
ventas?

14.- Un orfebre fabrica dos tipos de joyas.
La unidad de tipo A se hace con 1 g de oro y 1,5 g de plata y se
vende a 25 €. La de tipo B se vende a 30 € y lleva 1,5
g de oro y 1 g de plata. Si solo se dispone de 750 g de cada
metal, ¿cuántas joyas ha de fabricar de cada tipo
para obtener el máximo beneficio?

15.- Se desea realizar una mezcla con dos
sustancias, A y B, que ha de contener como mínimo 10
unidades de cada una de ellas. Estas sustancias nos las venden
dos proveedores en forma de lotes. El lote del primer proveedor
es tal que los contenidos de B y de A están en
relación de 4 a 1 y hay una unidad de A. El lote del
segundo proveedor es tal que los contenidos de A y de B
están en relación de 4 a 1 y hay una unidad de B.
El primer proveedor vende cada lote a 10 € y el segundo al
doble. Ambos proveedores nos venden lotes enteros o fracciones de
ellos. ¿Qué número de lotes hemos de comprar
para que el coste sea mínimo?


16.- Un veterinario aconseja a un granjero
dedicado a la cría de aves una dieta mínima que
consiste en 3 unidades de hierro y 4 unidades de vitaminas
diarias. El granjero sabe que cada kilo de maíz
proporciona 2,5 unidades de hierro y 1 de vitaminas y que cada
kilo de pienso compuesto proporciona 1 de hierro y 2 de
vitaminas. Sabiendo que el kilo de maíz vale 0,3 € y
el de pienso compuesto 0,52 €, se pide:
a) ¿Cuál es la
composición de la dieta diaria que minimiza los costes del
granjero? Explica los pasos seguidos para obtener la
respuesta.
b) ¿Cambiaría la
solución del problema si por escasez en el mercado el
granjero no pudiera disponer de más de 1 kilo diario de
pienso compuesto?
Razona la respuesta.


Enviado por:
Pablo Turmero