Los fluidos III

Introducción

El agua, el aire, el mar, la sangre, algunos nutrientes, lubricantes, combustibles etc., son fluidos ( líquidos y gases) que en nuestra vidas juegan un papel de gran importancia. Así se tiene que las propiedades de los fluidos, es decir de líquidos como gases se aplican tanto al flujo de aire a través de los tubos bronquiales como al flujo de sangre a través de los vasos sanguíneos El aprovechamiento de los recursos hidráulicos y el estudio de ellos por parte de la ingeniería nos lleva al buen uso de la energía hidráulica. Las estructuras hidráulicas, la ingeniería naval son factibles de analizarlas debido al estudio del comportamiento del agua.

El control y transmisión neumática, la refrigeración, el aire acondicionado, la meteorología, el aire comprimido son factibles de analizarlos debido al estudio del comportamiento del aire.

El estudio de la mecánica de fluidos resuelve la problemática de la construcción de las redes de distribución de agua, de gas, de oleoductos, de gasoductos.

En esta unidad se analizará brevemente el comportamiento de los fluidos. La mecánica de fluidos estudia los fluidos tanto en estado de equilibrio o reposo, que es la hidrostática, como también en estado de movimiento, que es la hidrodinámica.

La mecánica de fluidos moderna nace con Prandtl en las primera década de este siglo; es él el que realizó la síntesis entre la hidráulica práctica y la hidrodinámica. A lo largo de los siglos son muchas las personas que han contribuido con su aporte para llegar hasta el desarrollo actual de esta ciencia, entre ellas podemos citar a Arquímedes, Torricelli, Pascal, Newton, Bernoulli, Euler, Lagrange, Venturi, Poiseulli, Weisbach, Reynold, Froude, Stoke y el más reciente Prandtl.

En el siguiente punto se darán algunas definiciones y propiedades básicas para entender el comportamiento de los fluidos.

1.Propiedades de los fluidos y definiciones

Los conceptos de densidad y de viscosidad desempeñan papeles importantes en el movimiento de los fluidos, tanto en conductos cerrados como abiertos; la tensión superficial influye en el movimiento de pequeños chorros y ondas, altera el movimiento en los conductos de pequeña sección. el cuerpo humano emplea los tensioactivos para reducir la tensión superficial en el revestimiento mucosos de los alvéolos pulmonares que son las pequeñas cavidades en las que terminan los tubos bronquiales de los pulmones. La presión de vapor también desempeña un papel importante en el cambio de la fase de líquido a gas.

¿Que se entiende por fluido? Generalmente se acostumbra a decir que un fluido es una sustancia que se caracteriza por poseer un volumen definido, pero no una forma definida. Una definición adecuada de este concepto se basa en el concepto de fatiga o esfuerzo tangencial ((t).

Esfuerzo tangencial ((t). : Tomando un elemento de área pequeño dA sobre el que actúa un elemento de fuerza en general se define el esfuerzo por la expresión . Los esfuerzos pueden ser normales o bien tangenciales

Para los esfuerzos tangenciales o de cortadura ((t), la fuerza es paralela o tangente al área sobre la que actúa; se producen tanto en los sólidos como en los fluidos.

Para el caso de esfuerzos normales ( ), la fuerza es normal ( perpendicular ) al área que resiste la deformación, pudiendo ser de compresión , es decir , la fuerza se aplica contra la superficie, o esfuerzo de tracción, es decir, la fuerza se aplica en la superficie pero "tirando" de ella hacia fuera.

En la figura se muestran las dos fuerzas, una saliendo y la otra entrando a la superficie ?A

Los líquidos no soportan esfuerzo de tracción, pueden sólo soportar esfuerzos de compresión.

1.- Fluido

Se define como fluido a la sustancia que se deforma continuamente al ser sometida a un esfuerzo tangencial o cortante, no importando cuan pequeño sea este, o bien, sustancia que no acepta esfuerzo cortante cuando éste está en equilibrio o reposo.

Los fluidos están compuestos de moléculas que se encuentran en movimiento constante. El fluido está idealmente compuesto de una sustancia infinitesimal divisible, un continuo, no preocupándose por el comportamiento individual de las moléculas. La mecánica estadística y la teoría cinética de los gases contempla el estudio a nivel molecular.

2.- Presión

De acuerdo a lo expuesto en la definición de esfuerzo, se define presión media como la razón entre la fuerza normal que actúa sobre un área plana y dicha área:

La presión en un punto es el límite de la presión media, cuando el elemento de área tiende a cero (la presión no es una magnitud vectorial).

2.a Unidades de presión en los diferentes sistemas: La dimensión para medir presión es : (F) (L)-2 En el S.I. se llama Pascal ( Pa ) 1 Pa = 1 N/m2 En el C.C.S. se llama Baria 1 Baria = 1 Dina/cm2 En el sistema técnico gravitacional no tiene nombre especial y es kgf-/m2 Como unidad práctica para medir presión se usa la altura equivalente de columna de algún líquido determinado, se suele usar el mm columna de mercurio que se le llama Torr.

l milímetro de Hg = l Torr.

2.b Medición de la presión sanguínea

El instrumento que mide presión sanguínea se conoce con el nombre de esfigmomanometro.

El esfigmomanometro de mercurio corresponde a una variante del manómetro de tubo en U abierto donde el recipiente sustituye a la mitad del tubo en U y es lo suficientemente grande para que las variaciones en el nivel del mercurio puedan ignorarse. La lectura de presión se hace en el nivel superior de la columna de mercurio.

El brazalete se coloca alrededor del brazo a la altura del corazón, además como el antebrazo tiene un solo hueso, da facilidad para localizar la arteria humeral. La presión en el brazalete se eleva por encima de la presión sanguínea sistólica inyectando aire dentro de él, lo que se hace hasta que la arteria humeral quede aplastada y no permite el paso del flujo de sangre en las arterias del antebrazo, luego se suelta lentamente el aire y simultáneamente se usa el estetoscopio para escuchar la vuelta del pulso.

El primer sonido corresponde con la presión sistólica, ya que a esa presión máxima la sangre se abre paso a través de la arteria aplastada. Este valor se mide en la diferencias de alturas (expresada en mm ) de las columna de mercurio.

Después se deja escapar más aire del brazalete para bajar más la presión. El sonido se deja de escuchar cuando la presión iguala a la presión diastólica ya que la sangre a baja presión es capaz de pasar a través de la arteria del brazo.

Las presiones sanguíneas se expresan habitualmente como razones de presiones sistólica/diastólica y los valores típicos para un adulto sano en estado de reposo son aproximadamente 120/80 torr o bien 16/11 kPa

3. Densidad absoluta (p)

Los fluidos son agrupaciones de moléculas, separadas en los gases y más próximas en los líquidos, la distancia entre las moléculas es mucho mayor que el diámetro molecular. La densidad absoluta se define como siendo ( = 10-9 mm3 para líquidos y gases a la presión atmosférica.

En forma macroscópica podemos decir que la densidad (se lee rho ) es el cuociente entre la masa y su volumen respectivo Unidades de densidad absoluta: S.I. : Kg/ m3 ; C.G.S. : gr / cm3

4.- Densidad relativa (pr )

En algunas oportunidades se da la densidad relativa la cual se define como la razón entre la densidad absoluta de una sustancia y la densidad absoluta de otra sustancia que se toma como patrón., la densidad relativa de una sustancia es un número abstracto La densidad absoluta del agua, a la temperatura aproximada de 4°C y 1 atmósfera de presión es de:

1 gr/cm3 = 103 kg/m3 La densidad del aire a 0°C y una atmósfera de presión es de 1,293 kg/m3

Revise la tabla 7-2 del libro Física para ciencias de la vida del autor Cromer, en sus apuntes registre las densidades del agua destilada, de la sangre, del mercurio, del cobre, del hierro, del aire, plasma sanguíneo, etc

Anomalia del agua

Por su característica, los líquidos son prácticamente incompresibles y la mayoría de ellos, al aumentar la temperatura disminuye su densidad. Sin embargo, en toda regla hay excepción y, en este caso, el agua presenta esta excepción.

Entre 0 y 4° C el agua presenta una anomalía.

El gráfico adjunto muestra la relación de volumen versus temperatura para una cierta cantidad de agua de volumen inicial Vo.. Del gráfico se deduce que a los 4ºC el volumen de agua, el cual no ha cambiado de masa, toma el menor volumen, en consecuencia su mayor densidad.

Una consecuencia es que el hielo tiene una menor densidad (0,92 gr/cm3) y flota en agua tal como usted lo ha observado más de alguna vez.

Averigüe algo más acerca de esta anomalía , a nivel molecular.

5. Peso específico (p)

Este concepto es similar al de densidad, pero en vez de considerar la masa, se toma en cuenta el peso.

Se define como el peso de la unidad de volumen

o bien

La dimensión es (F/L3 ) ; en los distintos sistemas se mide a N/m3 ; Dina/cm3 ; kgf-/m3 .

6.- Viscosidad dinámica o absoluta (p)

Al analizar cuerpos en movimiento que se desplazaban sobre una superficie, aparecía la fuerza de roce. En los fluidos en movimiento , el roce está asociado a otro concepto, este concepto es el de viscosidad , fuerzas viscosas, el cual deberá de ser tomada en cuenta a la hora de realizar el balance energético.

Se entiende por viscosidad dinámica al rozamiento interno desarrollado, cuando una parte del fluido se mueve relativamente a una parte adyacente. El coeficiente de fricción interna del fluido se llama viscosidad y se designa por ( ( se lee muu).

En los fluidos, la deformación aumenta constantemente bajo la acción del esfuerzo cortante o tangencial , por pequeño que éste sea.

En la figura para poner en movimiento la superficie plana A1 con una velocidad constante se requiere aplicar una fuerza externa sobre la lámina A1 igual y contraria a la fuerza de rozamiento que ejerce el fluido sobre A1.

Suponiendo que el fluido contenido entre las placas está compuesto por una serie de capas, se observa que la capa de fluido en contacto con la superficie A1 se adhiere a esta superficie y se mueve con ella por lo que no hay movimiento de esta capa de fluido respecto a la superficie A1. Luego, esta capa de fluido adyacente a A1, que no desliza sino que se mueve con la misma velocidad con que se mueve A1, arrastra a la capa de fluido que se encuentra inmediatamente debajo de ella. La segunda capa se mueve por efecto del movimiento de la primera capa, con una velocidad menor y arrastra en su movimiento a la capa siguiente. Este proceso se repite hasta que se llega a la capa de fluido que se encuentra en contacto con la superficie A2 la que está en reposo por lo que la capa que está en contacto con esa capa tendrá velocidad nula.

De acuerdo con este estudio se puede establecer la siguiente expresión para la fuerza viscosa de un fluido:

donde ( es una constante característica del fluido llamada viscosidad dinámica. Esta expresión muestra que la fuerza viscosa, es proporcional a la velocidad al área de A1 e inversamente proporcional a la separación d entre las placas.

En general la viscosidad es una característica intrínseca del fluido, para los líquidos es directamente dependiente de la temperatura.

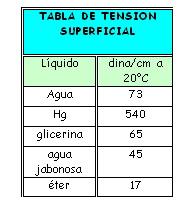
TABLA DE VISCOSIDADES

– Para un fluido ideal ( = 0 . Para un fluido real ( ( 0

Para un fluido en reposo, el fluido siendo real se comporta como ideal.

La viscosidad dinámica de los gases aumenta con la temperatura, en cambio en los líquidos disminuye y la viscosidad dinámica de los fluidos es prácticamente independiente de la presión.

Unidad para ( en distintos sistemas: En el S.I. : N s/m2 En el C.G.S. : Dina s/cm2 , esta unidad recibe el nombre de Poise.

El centipoise ( cP ) es la centésima parte del Poise.

7. Viscosidad cinemática ( p )

Es la viscosidad dinámica referida a la densidad del fluido.

Este concepto resulta de utilidad cuando se trabaja en hidrodinámica con algunos parámetros adimensionales, como lo es el número de Reynolds.

Averigue acerca de la experiencia que George Stoke realizó para calcular el coeficiente de viscosidad dinámica de algunos líquidos.

8. Tensión superficial

Cuando se analizan las superficies de los líquidos se observa algunas propiedades especiales.

Al igual que en los sólidos se da la cohesión molecular en los líquidos, es decir la fuerza de atracción entre las moléculas. Esas atracciones hacen que los líquidos presenten superficies que están bien definidas. Además de las fuerzas atractivas del líquido, las moléculas de los líquidos experimentan fuerzas repulsivas o atractivas con moléculas de otras sustancia como por ejemplo con las de la vasija que contiene al líquido, o bien, con otro líquido con el cual se ponga en contacto.

En general se puede decir que la Tensión Superficial es una fuerza que produce efectos de tensión en la superficie de los líquidos, en la superficie de separación de dos fluidos no miscibles, líquido con un gas o con un contorno sólido como una vasija.

Esta fuerza es debida a la cohesión intermolecular y la fuerza de adhesión del líquido al sólido.

La tensión superficial se manifiesta como si el líquido creara una fina membrana La molécula B, que muestra la figura, está rodeada por otras de su misma especie, es atraída por las vecinas de igual forma encontrándose en equilibrio, la fuerza de cohesión molecular no produce efecto resultante alguno.

Las moléculas A y C están rodeadas por otras moléculas. Hay una fuerza de cohesión dirigida hacia el interior del líquido. Sobre toda la capa próxima a la superficie del líquido actúan fuerzas normales a ellas y dirigidas hacia el interior. Las moléculas están más juntas y aparecen fuerzas repulsivas, las cuales equilibran a las de compresión originadas por la capa superficial.

Los fenómenos debido a la tensión superficial pueden explicarse estudiando una película delgada estirada, de algún líquido (agua de jabón, saponina).

En la figura puede verse el método clásico que permite investigar la tensión superficial. Hay una membrana líquida encuadrada en el marco ABCD.

Para mantener la membrana estirada en equilibrio se debe aplicar una fuerza perpendicular a la línea EH (que es una barra móvil) y tangente a la superficie del líquido. A esta fuerza se le llama tensión superficial y es tanto mayor su módulo, mientras mayor sea l, de modo que F ( 2 l o F = ( 2 l (1) donde ( es el coeficiente de tensión superficial y se puede expresar como ( = F/ l, siendo l el largo total sobre el que actúa la fuerza .

Si se quiere calcular el trabajo que se debe hacer para aumentar el área de la película superficial en un ldx, nos recordaremos de la definición para un diferencial de trabajo que es dW = F. dx, entonces :

teniendo en cuenta la ecuación (1) F = ( 2 l

se tendrá dW = ( 2 l dx de la figura dA =2 l dx luego dW =( dA ó

El fenómeno de la capilaridad se origina por la tensión superficial y por el valor de la relación entre el módulo de la fuerza de adhesión entre líquido y sólido con el módulo de la fuerza de cohesión del líquido.

Un líquido que moja al sólido tiene mayor adhesión molecular que cohesión molecular, en este caso la acción de la tensión superficial es la causa de que el líquido se eleve dentro de un pequeño tubo vertical que se sumerja parcialmente en él.

Un líquido que no moja al sólido tiene menor adhesión que cohesión, en éste la tensión superficial tiende a hacer descender el menisco en un pequeño tubo capilar.

Estos fenómenos de capilaridad, de que moje o no moje el líquido al sólido, debe tenerse en cuenta en la lectura de los manómetros de líquido.

Una columna de líquido puede quedar sostenida en un tubo delgado de vidrio (tubo capilar) debido a las fuerzas adhesivas y cohesivas que actúan sobre él. Es lo que se conoce como "acción capilar" La superficie del líquido hace contacto con la pared del tubo en una extensión igual al perímetro del tubo, es decir una longitud de 2( R. La fuerza de tensión superficial F forma un ángulo ( con la vertical, luego la fuerza resultante hacia arriba es F= ( 2( R cos (. al igualar este expresión al peso de la columna de líquido que es sostenida por esta fuerza, se tiene:

, luego

Transporte de agua en los árboles.

La evidencia sostiene en forma clara la teoría que el agua asciende en los árboles por presión negativa, la naturaleza produce de un modo habitual tales tipos de presiones." El agua en las plantas es conducida a través del xilema, un sistema de capilares formado por células muertas que han perdido el citoplasma. "Estos capilares tiene diámetros comprendidos entre 0,05 y 0,5 mm y pueden subir hasta una altura de 75m o más ." Podría pensarse que el agua sube por medio de la acción capilar. Sin embargo, la altura h a que sube el agua en un capilar de radio r = 0,02mm es 0,74m, la cual no alcanza la altura necesaria. " . Se han realizado medidas que permiten determinar la presión en el xilema de árboles altos las cuales demuestran que la presión en la mayoría de las veces es negativa en la copa de un árbol y que aumenta a medida que se va descendiendo ( ** Física. para ciencias de la vida : Alan Cromer)

Burbujas Una burbuja es una superficie esférica de líquido. En ella se encuentra presente la tensión superficial, la cual hace tender a encoger la burbuja. A esta situación se opone la presión que está al interior de ella ( pi) la cual es mayor que la presión externa( po).

Se puede llegar a demostrar que la relación entre la presión
externa , la presión interna y el coeficiente de tensión superficial en una burbuja de radio R viene dada por la ecuación (1) y para una gota viene dada por la ecuación (2):

Tension superficial en los pulmones

Los alvéolos , que son pequeños saquitos de aire en los pulmones son capaces de expansionarse y contraerse unas 15000 veces al día en un adulto mayor. Por medio de la membrana de los alvéolos se produce el intercambio de oxigeno y de dióxido de carbono y la tensión de las paredes se debe al tejido de la membrana y a un líquido que contiene un tensioactivo ( lipoproteina) que es el agente que da a la membrana la elasticidad suficiente para desarrollar los ajustes necesarios en la tensión de la pared.

En general un tensioactivo es una sustancia que reduce la tensión superficial de un líquido.

Los alvéolos pulmonares en las que terminan los tubos bronquiales de los pulmones son diminutas cavidades del orden de 10-2 cm de radio. La presión que se produce en una inspiración normal es aproximadamente de 3 Torr ( 3 mm de Mercurio) bajo la presión atmosférica ( 760 mm de Hg), lo que permite que el aire llegue a ellos por medio de los tubos bronquiales. Los alvéolos están recubiertos de un fluido de tejido mucoso que tiene aproximadamente una tensión superficial de 0,05N/m.

Durante una inspiración el radio de los alvéolos se extiende de 0,5x 10-4m hasta 1 x 10-4 m.

Se puede determinar la diferencia de presión ( presión manométrica )necesaria para hinchar un alvéolo la cual sería:

pi – po = = 15 mm de Hg

ya que la equivalencia entre la unidad de presión pascal y mm de Hg es de 101300Pa = 760mm de Hg Este resultado nos dice que la presión manométrica fuera del alvéolo debe ser 15mm de Hg menor que la presión dentro de él , es decir debiera ser de 18 mm por debajo de la atmosférica ( -18 mm Hg).

La presión manométrica que hay entre los pulmones y la cavidad pleural es de aproximadamente de -4 mm de Hg, es esta presión negativa la que mantiene los pulmones en contacto a las paredes de la cavidad pleural. Este valor nos dice que la diferencia de presión real es tan solo de 1 mm de Hg, es decir, 15 veces menor que la que se necesita para dilatar un alvéolo.

Los bebes recién nacidos tienen tan aplastados sus alvéolos que se necesita una diferencia de presión de unos 30 mm de Hg para inflarlos por primera vez, es decir, el esfuerzo que se hace la primera vez para vencer la tensión superficial es suficientemente grande.

9. Presión de vapor

Cuando los líquidos se evaporan, las moléculas se escapan de la superficie del líquido ejerciendo una presión parcial en el espacio adyacente conocida como presión de vapor, dependiendo de la temperatura y aumentando con ella.

Cuando la presión que actúa sobre el líquido es igual a su presión de vapor, se presenta la ebullición.

Estadistica de los fluidos

Recordemos que para un fluido que está en reposo, no hay fuerza cortante o tangenciales, únicamente pueden actuar fuerzas normales ( presión).

1. ESTUDIO DE LA PRESIÓN Y DE SUS VARIACIONES A TRAVÉS DEL FLUIDO

A. PRESIÓN EN UN PUNTO En un punto al interior de un fluido que está en reposo, la presión es la misma cualquiera que sea la orientación desde donde se haga la medida.

B. VARIACIÓN DE LA PRESIÓN EN UN FLUIDO EN REPOSO La presión al interior de un fluido en reposo tiene variaciones a lo largo de la vertical solamente. En planos horizontales no hay variación de la presión.

Podemos afirmar que: ''la presión en todos los puntos situados en un mismo plano horizontal en el seno de un fluido en reposo es la misma''. Para demostrar esta afirmación, imaginemos al interior de un fluido en reposo un "cilindro de fluido" horizontal de largo l y área basal infinitesimal dA. Las únicas fuerzas que actúan en dirección axial son las fuerzas de presión luego :

Esto significa que en puntos cualquiera de un mismo plano horizontal en una masa continua de un fluido en reposo, existe la misma presión ( los puntos A y B son puntos cualquiera del plano horizontal).

C. Presión al interior de un liquido

En el punto anterior, se vio que no hay variación de la presión en un plano horizontal, luego si es que hay variación, ésta debe ser en la vertical.

En forma cuantitativa se puede obtener una expresión que nos permita ver como varía la presión con la profundidad en un líquido de densidad constante. Para ello, consideremos una cierta cantidad de fluido en forma de prisma de sección basal A y de altura h.

Calculemos la presión p en la cara basal inferior

La fuerza que soporta debida al líquido es la fuerza peso, es decir mg. Pero la masa la podemos expresar como el producto entre la densidad y el volumen (V ( de acuerdo a la definición de densidad ( = m/ V) . Por otra parte el volumen del prisma es base por altura, luego el volumen es V = A h. De acuerdo a estas consideraciones se tendrá:

Es decir, hemos llegado a que la presión es directamente proporcional a la profundidad h y a la densidad del líquido. Mientras más profundo, mayor es la presión.

Si se quiere obtener la presión total a una profundidad h, se debe además considerar la presión existente en la superficie del líquido, como por ejemplo la presión atmosférica (po) Para ese caso la presión absoluta a la profundidad h será:

"p" es la presión absoluta en un punto al interior del líquido. "po" es la presión atmosférica o barométrica. "h" es la profundidad del punto con relación a la superficie libre.

En un líquido en reposo que ocupa una determinada región, la presión varía sólo con la vertical y es independiente de la forma del depósito. La figura siguiente muestra un depósito que tiene dos líquidos, y de acuerdo a lo visto se tiene que:

La presión para fluidos es compresible. es decir, para los gases, la expresión anterior no es válida( no se analizará esos casos)

d.- Atmosfera estandar o normal La presión atmosférica se mide con un barómetro. Un barómetro de mercurio es esencialmente un tubo delgado cerrado en uno de los extremos que se llena con mercurio que se coloca invertido en un recipiente que contiene mercurio como se indica en la siguiente figura

Parte del mercurio sale del tubo pero la presión atmosférica sobre la superficie del recipiente, equilibra una columna de mercurio de altura h. De aquí se tiene que patm = po = (gh, donde ( es la densidad del mercurio y h es la altura de la columna.

Se ha adoptado una atmósfera normal que aproximadamente coincide con la atmósfera real de varios puntos de la tierra con las siguientes características:

Po = 101.3 Kpa = 76 cm de Hg = 10.34 metros columna de H20 = 14.7 Lb/plg2 Este valor es válido a nivel del mar. En zonas más elevadas la presión es menor, es así por ejemplo que la ciudad de Santiago, la cual se encuentra a una altura aproximada de 560m sobre el nivel del mar, la presión es aproximadamente de 710mm de Hg.

e.- Unidades y escalas de medidas de presión Las presiones se expresan con respecto a un nivel de referencia. Si este nivel es el vacío, la presión se llama presión absoluta y es siempre positiva, y cuando se toma como origen la presión atmosférica local, se llama presión manométrica.

La presión manométrica es la diferencia entre la presión absoluta y la presión atmosférica local, la cual puede ser positiva o negativa.

f.- Instrumentos de medida de presión

Barómetro : mide la presión atmosférica. Averigue acerca del Barómetro de Torricelli y el aneroide.

Manómetro : mide las sobrepresiones o presiones manométricas positivas.

¿Es correcto pedirle al bombero de una estación de servicio de gasolina que le ponga 28 Lb a los neumáticos de un automóvil. Explique su respuesta. ¿Qué tipo de presión es la que se está midiendo?

Manómetro Diferencial : mide la diferencia de presión entre dos puntos.

Micromanómetro : mide presiones muy pequeñas.

Tubos piezométricos :

Son instrumentos para medir la presión estática en un líquido, midiendo la ascensión del mismo líquido en el tubo y no requiriendo otro líquido manométrico distinto. Son de gran precisión y sirven para medir presiones manométricas que no exceden mucho la presión atmosférica. ¿A que se debe esto?

Manómetro en U de líquido :

Sirve para medir sobrepresiones, también puede servir para medir depresiones. En la figura hay una sobrepresión. El líquido manométrico se debe escoger de densidad adecuada a las mediciones que se destina el manómetro.

Manómetro diferencial:

Mide la diferencia de presión entre dos puntos.

g.- Fuerza de flotacion o empuje Es un hecho experimental conocido, que un cuerpo sumergido en un fluido total o parcialmente, recibe una fuerza resultante vertical hacia arriba la que recibe el nombre de fuerza de flotación ó empuje Se puede demostrar que la fuerza de flotación o empuje es equivalente al producto entre: la densidad del fluido ((), el volumen del cuerpo sumergido ( total o parcialmente Vcs) y la aceleración de gravedad (g):

E = (L g VC.S

Para demostrar esto tomemos un cuerpo sólido de forma cilíndrica de altura h = (h 2 – h1) y base A, sumergido en un líquido flotando como muestra la figura. Recordemos que las fuerzas de presión son perpendiculares a la superficie y contra la superficie.

Las fuerzas horizontales se anulan por ser simétricas.

La fuerza de presión que ejerce el líquido de tipo vertical sobre la parte superior del cilindro es: Fl = p1A = (L g h 1 A , dirigida hacia abajo y la fuerza que actúa sobre la parte inferior del cilindro que es

F2 = P2A = (L g h 2 A , dirigida hacia arriba.

Entonces la fuerza resultante será F2 – Fl = (L g h 2 A – (L g h 1 A = (L g A ( h 2 – h 1 ) = (L g A h = (L g VCS.= EMPUJE , Esta fuerza resultante es la que ejerce el líquido y se le conoce como fuerza EMPUJE y es equivalente al peso del líquido que se desplaza cuando entra el cuerpo total o parcialmente Esto se puede ver que es así ya que : como (= m / V y m = (. V reemplazando en la ecuación anterior F2 – Fl = g (L VCS . = g m

FLUIDO = EMPUJE

Esto significa que el empuje es equivalente al peso de un volumen de fluido donde está sumergido, volumen que es igual al del cuerpo sumergido total o parcialmente.

Podemos enunciar lo que se conoce también como PRINCIPIO DE ARQUIMEDES: " Un cuerpo sumergido total o parcialmente experimenta una fuerza empuje hacia arriba, igual al peso del fluido desplazado ". Si esta fuerza de flotación o empuje que actúa hacia arriba sobre el cuerpo que está sumergido es igual al peso del cuerpo, entonces el cuerpo flota "entre aguas" o bien parcialmente emergiendo como lo hace por ejemplo un trozo de hielo en agua:

EMPUJE = PESO

Si la fuerza es menor que su peso, el cuerpo se hundiría.

Entonces para un cuerpo de densidad (S , cuyo peso es PESO = (S g VS , el cual flota en un líquido de densidad (L , se tiene que: (1) (L g VCS.= (SgVS ( 2 ) (L VCS.= (SVS La ecuación (2) permite establecer una relación que nos indica que parte es la que "aflora" para un cuerpo que está parcialmente sumergido y que está en estrecha relación entre las densidades del sólido y del líquido.

Por ejemplo, para un trozo de hielo que se encuentra flotando en agua, se puede saber que parte del volumen total del trozo es la que está sumergida, Para ello se tiene como dato que la densidad del agua es de 1gr/ cm3 y la del hielo es de 0,92gr/ cm3.

PESO = EMPUJE

(HIELO g VC = (LIQ g VCS 0,92 x Vc = 1x Vcs Vcs = 0,92 Vc

Es decir, el 92% del trozo de hielo está sumergido , y sólo el 8% es lo que emerge o se ve

Dinamica de los fluidos

Introducción La dinámica de los fluidos es el estudio de un fluido en movimiento y de las fuerzas que lo producen.

Una de las formas de describir el movimiento de un fluido fue desarrollado por Lagrange (1707 -1813) y es una generalización directa de los conceptos de la mecánica de las partículas, pero algo complicado

Otra forma más conveniente de analizar el movimiento de los fluidos fue desarrollada por Leonard Euler (1707-1813), en él se especifica la densidad y velocidad del fluido en cada punto del espacio y en cada instante.

Clasificacion de los flujos Al movimiento de un fluido se le llama flujo.

Los flujos pueden clasificarse de diversas formas, una de ellas es:

a) viscoso y no viscoso b) laminar y turbulento c) permanente y no permanente d) incompresible y compresible e) irrotacional y rotacional f) unidimensional

Flujo viscoso: es aquel en el cual los efectos viscosos, es decir, el roce, son importantes.

Flujo laminar: el fluido se mueve en láminas o capas paralelas.

Flujo turbulento: las partículas fluidas se mueven siguiendo trayectorias muy irregulares.

Flujo permanente: las propiedades y características del flujo son independientes del tiempo. Esto significa que no hay cambios en las propiedades y características del flujo en un punto al transcurrir el tiempo, pero si puede haber cambio de un punto a otro del espacio.

Flujo incompresible : son aquellos flujos en los cuales las variaciones de la densidad son pequeñas y pueden despreciarse, luego la densidad es constante.

Flujo irrotacional : es aquel flujo en el cual un elemento de fluido en cada punto del espacio no tiene velocidad angular respecto de ese punto.

Flujo unidimensional : es aquel en el cual pueden despreciarse las variaciones de las propiedades del flujo en dirección perpendicular a la dirección principal del flujo; otra forma de definirlo es la siguiente: todas las propiedades y características del flujo depende de sólo una variable espacial. De acuerdo a la clasificación anterior, un flujo puede ser por ejemplo: no viscoso permanente, incompresible; viscoso laminar.

Fluido ideal El concepto de Fluido ideal es útil en el estudio de la dinámica de fluidos. Se trata de un fluido imaginario que no ofrece resistencia al desplazamiento (no viscoso), es permanente, irrotacional, no se comprime y es unidimensional.

Definiremos a continuación los conceptos de línea de corriente y tubo de corriente o vena líquida.

Linea de corriente

Un flujo se representa comúnmente en forma gráfica mediante líneas de corriente, A la trayectoria seguida por una partícula de un líquido en movimiento se le llama línea de corriente, estas son curvas tales que la velocidad es tangente a ella en cada punto.

Tubo de Corriente

Es un conjunto de líneas de corriente que pasan por el contorno de un área pequeñísima (infinitesimal dA). De acuerdo a la definición de línea de corriente no hay paso de flujo a través de la superficie lateral del tubo de corriente .

Caudal

Se define como caudal volumétrico (Q) al cuociente entre el volumen (V) que pasa por una determinada sección o área y el tiempo (t) que demora en pasar ese volumen. Así por ejemplo si 20 litros de un líquido atraviesan una sección en 4 (s), entonces el caudal es de:

Esta expresión de caudal puede tomar otra forma, para eso se supone que la velocidad es la misma para todos los puntos de la sección ó área A,

Si v es la velocidad con que el líquido atraviesa la sección A, la distancia que recorre en un intervalo de tiempo (t es equivalente a la distancia

Por otra parte, el volumen lo podemos expresar como el de un cilindro de base A y altura luego la expresión para el caudal será:

Es decir el caudal de líquido que atraviesa la sección A en un tiempo (t puede también ser expresado como el producto entre la velocidad (rapidez V) por la sección o área que atraviesa.

La forma que toma el principio de conservación de la masa en un fluido en movimiento en régimen permanente, unidimensional, incompresible, irrotacional y no viscoso, es decir, de un fluido ideal, es la

ecuación de continuidad.

Ecuación de continuidad

Como no puede haber paso de fluido a través del tubo de corriente y además si no hay fuentes ni sumideros dentro del tubo, el caudal volumétrico ( Q) a la entrada y salida del tubo es el mismo, luego se tiene que:

El producto A v es constante

Esto significa que para un caudal determinado, la rapidez con que se desplaza el líquido es mayor en las secciones más pequeñas. Sección y velocidad son inversamente proporcionales.

De acuerdo con la ecuación de continuidad para flujo compresible

Qentrante = Qsaliente

De un modo similar se puede establecer que la masa que pasa por unidad de tiempo debe permanecer constante. Esto se conoce como caudal másico

Se puede demostrar que el caudal másico también es igual al producto entre la densidad, la rapidez y el área de la sección, es decir, ( A v Como el caudal másico es el mismo en la sección 1 y 2, entonces se tiene que :