
Un sistema binario se caracteriza por tener dos valores posibles que, en términos de voltaje, se corresponden a dos valores de tensión, los que se representan numéricamente por un “1” y por un “0”.
Generalmente, la “lógica positiva” hace corresponder un valor de tensión alto al “1” y un valor de tensión bajo al “0” (y viceversa para la “lógica negativa”):
Introducción a los sistemas digitales
Sistemas binarios
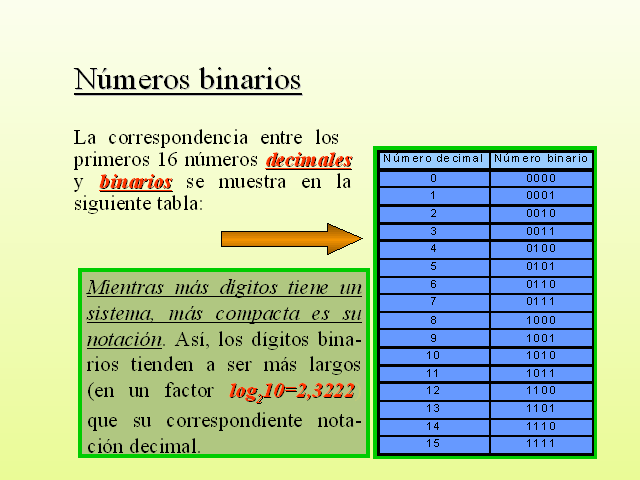
Números binarios
La correspondencia entre los primeros 16 números decimales y binarios se muestra en la siguiente tabla:
Mientras más dígitos tiene un sistema, más compacta es su notación. Así, los dígitos bina-rios tienden a ser más largos (en un factor log210=2,3222) que su correspondiente nota-ción decimal.

Las principales razones por las cuales utilizar sistemas de representación binaria son:
Porqué usar la representación binaria
Los sistemas de procesamiento de información se construyen en base a conmutadores;
Los procesos de toma de decisión, en un sistema digital, son binarios; y
Las señales binarias son más confiables que las que tienen más niveles de cuantificación.

Conmutadores
Porqué usar la representación binaria
Supóngase un sistema de iluminación basado en dos interruptores o con-mutadores (como el que existe en la parte inferior y superior de una escalera):

Toma de decisiones
Porqué usar la representación binaria
Gran parte de los procesos de decisión tienen carácter binario
Un sistema puede ca-racterizarse lingüísti-camente como:
Si (S1=1 y S2=0) o (S1=0 y S2=1), entonces B=1; caso contrario, B=0.
Confiabilidad
Las señales binarias son mucho más confiables para ser transmitidas entre dos puntos distantes. Al usar sólo dos niveles de voltaje para representar un dígito, el sistema es más inmune a la presencia de ruidos.

Descripciones formales
Definición de modelos lógicos
Una descripción abstracta de un sistema digital, expresado con enunciados lógicos formales, se denomina “DISEÑO LÓGICO”.
Los símbolos más comunes son:
Usando estos símbolos, el circuito de encendido de la ampolleta puede representarse como:

Usando este tipo de representación, podría definirse la operatoria de un sumador binario como:
o, en forma simbólica (para el caso de la “suma”), por:
Definición de modelos lógicos

En caso de sistemas multivariables (varias entradas y salidas), “x” será un vector de entradas y habrá una función asociada a cada salida. Estas funciones también suelen denominarse “funciones booleanas”, ya que responden al “álgebra de Boole”.
Definición de modelos lógicos
Un comportamiento de un sistema combinacional puede expresarse formalmente como z=f(x), donde “z” representa la salida del sistema y “x” la entrada (para un sistema de una entrada y una salida).

Para el caso del circuito de la ampolleta:
Puede apreciarse que el comportamiento de un circuito combina-cional puede repre-sentarse también a través de una tabla conocida como “tabla de verdad”.
Definición de modelos lógicos

Componentes lógicos
Sistemas con conmutadores
Los conmutadores son elementos que pueden tener dos estados posibles (son adecuados para entender dispositivos lógicos).
Los tipos de conmutadores eléctricos más comunes son:

Circuitos de conmutación
Circuito AND
En la siguiente figura se muestra este tipo de circuito, junto con el símbolo lógico más utilizado para una compuerta AND y la tabla de verdad correspondiente.
(Gp:) FUENTE
(Gp:)
(Gp:) CARGA
(Gp:)
(Gp:) S
(Gp:)
(Gp:) 1
(Gp:)
(Gp:) S
(Gp:)
(Gp:) 2
(Gp:)
(Gp:) Circuito AND
(Gp:)
(Gp:) AN
(Gp:) AND
(Gp:)
(Gp:) Comp
(Gp:) uerta AND
(Gp:)
(Gp:) S
(Gp:)
(Gp:) 1
(Gp:)
(Gp:) S
(Gp:)
(Gp:) 2
(Gp:)
(Gp:) z
(Gp:)
(Gp:) z
(Gp:)
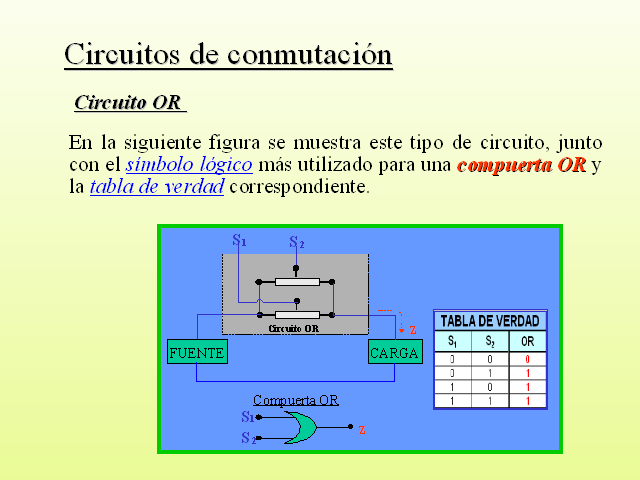
Circuitos de conmutación
Circuito OR
En la siguiente figura se muestra este tipo de circuito, junto con el símbolo lógico más utilizado para una compuerta OR y la tabla de verdad correspondiente.
(Gp:) FUENTE
(Gp:)
(Gp:) CARGA
(Gp:)
(Gp:) S
(Gp:)
(Gp:) 1
(Gp:)
(Gp:) S
(Gp:)
(Gp:) 2
(Gp:)
(Gp:) C
(Gp:) ircuito OR
(Gp:)
(Gp:) Compuerta OR
(Gp:)
(Gp:) S
(Gp:)
(Gp:) 1
(Gp:)
(Gp:) S
(Gp:)
(Gp:) 2
(Gp:)
(Gp:) z
(Gp:)
(Gp:) z
(Gp:)

Circuitos de conmutación
Circuito NOT
En la siguiente figura se muestra este tipo de circuito, junto con el símbolo lógico más utilizado para una compuerta NOT y la tabla de verdad correspondiente.
1

Expresiones lógicas
Para expresar las funciones lógicas asociadas a cada uno de los circuitos anteriores, se usan operadores lógicos.
Es importante tener en cuenta que los símbolos “.” y “+” son operadores lógicos y NO algebraicos.

Convenios de voltaje
Para la lógica TTL (“Transistor – Transistor Logic”) se ha determinado un convenio de voltajes, para especificar cuándo una entrada o salida se considera que tiene el valor lógico correspondiente.

Álgebra de Boole
Axiomas
Se definen a continuación:

Dos expresiones booleanas, E1 y E2 , se dicen que son equivalentes (es decir, E1 = E2 ) cuando, ante las mismas entradas, provocan las mismas salidas. Esto se puede comprobar a partir de la tabla de verdad, o bien, partiendo de una de ellas y aplicar álgebra de Boole, hasta llegar a la otra.
Equivalencia de expresiones booleanas
Ejemplo: Demostrar que E1 = E2 , donde:
¿es práctico usar la tabla de verdad para comprobarlo en este caso?

Una función lógica presenta una correspondencia “uno a uno” con un circuito lógico o con una tabla de verdad.
Correspondencia de la lógica combinacional
Sea la siguiente función lógica:
el circuito lógico y su tabla de verdad serán:

Representación de un sistema combinacional
Introducción
Los circuitos de Lógica Combinacional se caracterizan porque sus salidas se definen por una combinación lógica de sus entradas.

Minitérminos
Una función combina-cional distintiva son los minitérminos de “n” variables, y se los denota como mi. Son funciones booleanas cuya tabla de verdad tiene un “1” en la i-ésima fila, y un “0” en las restantes.

Forma canónica “Suma de minitérminos”
Dada una función z de “n” variables, cuya tabla de verdad tiene “1” en las filas a, b, …, k, y “0” en las demás. A partir de la definición de minitérmino, y usando la función OR, es evidente que:
z = ma + mb + … + mk
Ejemplo: Sean las funciones para z1=Z1(A,B,C,D), z2=Z2(A,B,C,D) y z3=Z3(A,B,C,D), caracterizadas por la siguiente tabla de verdad, determinar las funciones booleanas correspondientes:

Forma canónica “Suma de minitérminos”
Solución: Aplicando el concepto de minitérminos, las funciones busca-das serán:

Construcción algebraica
Cualquier expresión booleana puede convertirse a su forma canónica “suma de minitérminos” empleando las propieda-des del álgebra de Boole. A esta forma canónica también suele denominarse “Suma De Productos (SDP)”.
Ejemplo: Encontrar la forma canónica “suma de minitérminos” de:
Solución:
o bien:
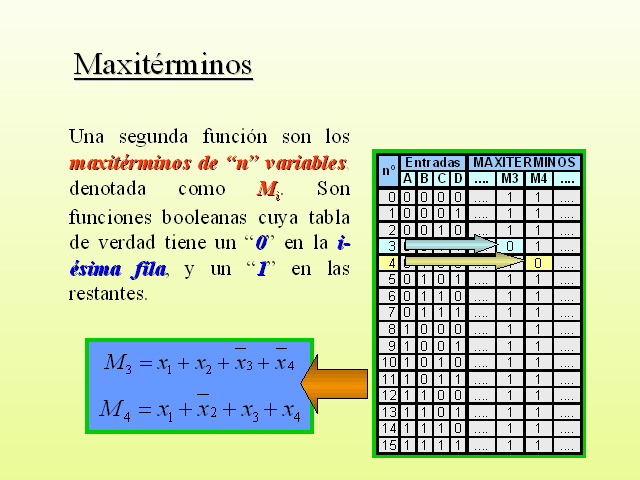
Maxitérminos
Una segunda función son los maxitérminos de “n” variables, denotada como Mi. Son funciones booleanas cuya tabla de verdad tiene un “0” en la i-ésima fila, y un “1” en las restantes.

Forma canónica “Producto de maxitérminos”
Toda función z tiene un conjunto único de maxitérminos Mi, que corresponde al conjunto de ceros que aparecen en la columna de salida de su tabla de verdad. La forma canónica de producto de maxitérminos será la función AND o producto lógico de estos maxitérminos. A esta forma canónica también suele denominarse “Producto De Sumas (PDS)”.
Ejemplo: Sea la la siguiente función booleana de tres variables:
la expresión canónica de producto de maxitérminos será:
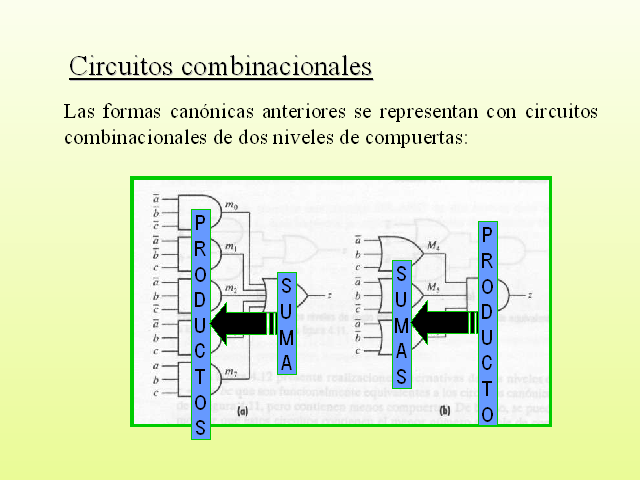
Circuitos combinacionales
Las formas canónicas anteriores se representan con circuitos combinacionales de dos niveles de compuertas:
(Gp:) SUMA
(Gp:) P
R
OD
U
C
T
O
S
(Gp:) DE
(Gp:) P
R
OD
U
C
T
O
(Gp:) SUMA
S
(Gp:) DE
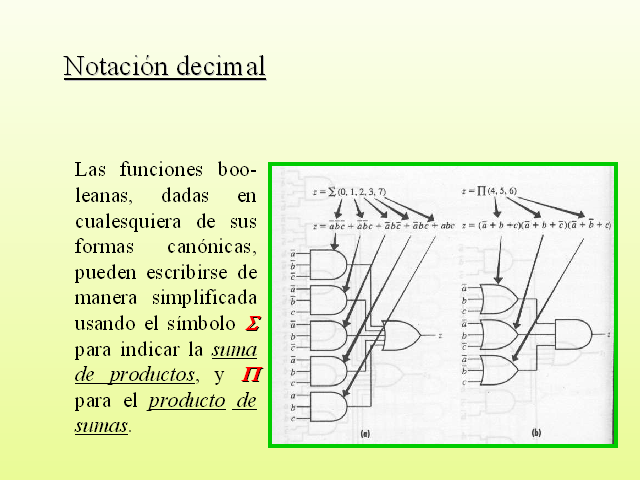
Notación decimal
Las funciones boo-leanas, dadas en cualesquiera de sus formas canónicas, pueden escribirse de manera simplificada usando el símbolo ? para indicar la suma de productos, y ? para el producto de sumas.

Formas de dos niveles
La profundidad de un circuito se mide por el máximo número de compuertas que una señal tiene que atravesar desde la entrada hasta la salida.
Las formas canónicas vistas tienen una profundidad de dos, considerando que se dispone de las entradas necesarias complementadas.
A pesar de que suelen ser los circuitos más rápidos que pueden lograrse con este tipo de implementación, esta disposición no implica ser la mejor desde el punto de vista del número de compuertas empleadas.

Formas de dos niveles
Los tres circuitos tienen la misma tabla de verdad.