Algebra de boole y compuertas

Representación de la Información
La computadoras necesitan almacenar datos e instrucciones en memoria
Sistema binario (sólo dos estados posibles)
Por qué?
Es mucho más sencillo identificar entre sólo dos estados
Es menos propenso a errores

Lógica digital
Los circuitos operan con valores [0, 1], que pueden ser interpretados lógicamente como [Falso, Verdadero].
Idea: implementar las operaciones lógicas y matemáticas combinando circuitos

George Boole, desarrolló un sistema algebraico para formalizar la lógica proposicional. El libro se llama “Análisis matemático de la lógica”.
George Boole
1815-1864
Algebra de Boole
El sistema consiste en un cálculo para resolver problemas de lógica proposicional (dos valores posibles [0, 1] y tres operaciones:
AND (y)
OR (o)
NOT (no) )

Las variables Booleanas sólo toman los valores binarios: 1 ó 0.
Una variable Booleana representa un el balor que puede tomar un bit, que como vimos quiere decir:
Binary digIT
Algebra de Boole

Operadores básicos
Un operador booleano puede ser completamente descripto usando tablas de verdad.
El operador AND es conocido como producto booleano (.) y el OR como co-producto booleano (+)
El operador NOT (¬ ó una barra encima de la expresión) conocido como complemento.

Funciones booleanas
Tabla de verdad de esta función:
El NOT tiene más precedencia que el resto de los operadores
Y el AND más que el OR

Identidades del Algebra de Boole

Ejemplo
Usando identidades booleanas podemos reducir esta función:

Fórmulas equivalentes
Varias fórmulas pueden tener la misma tabla de verdad
Son lógicamente equivalentes
En general se suelen elegir formas normales
Suma de productos:
F(x,y,z) = xy + xz +yz
Producto de sumas:
F(x,y,z) = (x+y) . (x+z) .(y+z)

Suma de Productos
Es fácil convertir una función a una suma de productos usando la tabla de verdad.
Elegimos los valores que dan 1 y hacemos un producto (AND) de la fila (negando si aparece un 0)
Luego sumamos todo (OR)
F(x,y,z) = (¬xy¬z)+(¬xyz)+(x¬y¬z)+(xy¬z)+(xyz)

Circuitos booleanos
Las computadores digitales contienen circuitos que implementan funciones booleanas
Cuando más simple la función más chico el circuito
Son más baratos, consumen menos, y en ocasiones son mas rápidos!
Podemos usar las identidades del algebra de Boole para reducir estas funciones.

Compuertas lógicas
Una compuerta es un dispositivo electrónico que produce un resultado en base a un conjunto de valores de valores de entrada
En realidad, están formadas por uno o varios transitores, pero lo podemos ver como una unidad.
Los circuitos integrados contienen colecciones de compuertas conectadas con algún propósito

Compuertas Lógicas
Las más simples: AND, OR, y NOT.
Se corresponden exactamente con las funciones booleanas que vimos

Compuertas lógicas
Una compuerta muy útil: el OR exclusivo (XOR)
La salida es 1 cuando los valores de entrada difieren.
Usamos el simbolo ? para el XOR.

Componentes digitales
Combinando compuertas se pueden implementar funciones booleanas
Este circuito implementa la siguiente función:
Simplificando las funciones se crean circuitos más chicos!

Ejemplo: La función Mayoría
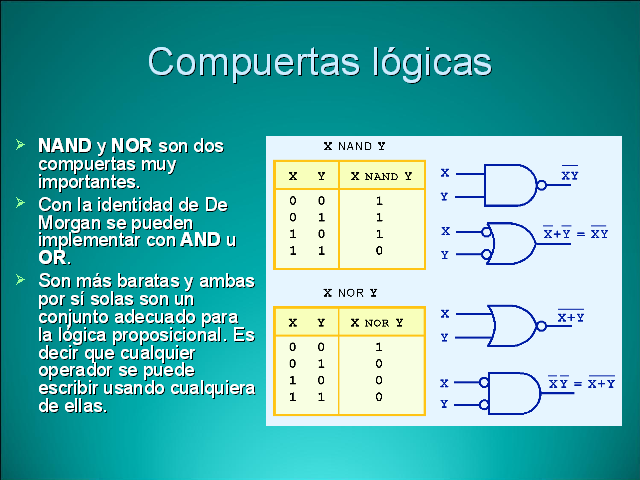
NAND y NOR son dos compuertas muy importantes.
Con la identidad de De Morgan se pueden implementar con AND u OR.
Son más baratas y ambas por sí solas son un conjunto adecuado para la lógica proposicional. Es decir que cualquier operador se puede escribir usando cualquiera de ellas.
Compuertas lógicas

NAND y NOR

Ejercicio
Ejemplo: NOT usando NAND
Utilizando solo NAND o NOR realizar circuitos con la misma funcionalidad que el AND y OR

Circuitos combinatorios
Producen una salida específica (casi) al instante que se le aplican valores de entrada
Implementan funciones booleanas
La aritmética y la lógica de la CPU se implementan con estos circuitos

Sumadores
Como podemos construir un circuito que sume dos bits X e Y?
F(X,Y) = X + Y (suma aritmética)
Que pasa si X=1 e Y=1?

Podemos usar un XOR para la suma y un AND para el acarreo
A este circuito se lo llama Half-Adder
Half-Adder
(Gp:) X
(Gp:) Y
(Gp:) ?
(Gp:) C
(Gp:) Half
Adder

¿Cómo se suman números de dos bits?
Ej:
1 1
+ 1 1
___________________
Full Adders

Full Adders
¿Cómo se suman números de dos bits?
Ej:
1
1 1
+ 1 1
___________________
0

¿Cómo se suman números de dos bits?
Ej:
1 1
1 1
+ 1 1
___________________
1 0
Full Adders

Full Adders
¿Cómo se suman números de dos bits?
Ej:
1 1
1 1
+ 1 1
___________________
1 1 0

(Gp:) Full Adder
(Gp:) X
(Gp:) Y
(Gp:) Ci
(Gp:) ?
(Gp:) Co
Full Adders
¿Cómo se suman números de dos bits?
Ej:
1 1
1 1
+ 1 1
___________________
1 1 0
En el caso de los Full Adders se asume que poseen una entrada más, el acarreo.

Cómo es la tabla de verdad de un Full Adder?
Podemos mejorar nuestro half-adder para considerar un “acarreo” en la entrada.
Full-Adder

¿Podemos adaptar nuestro half-adder para convertirlo en un full adder?
Full Adders

Half
Adder
X
Y
Ci
?
Co
Full Adder
Half
Adder
?
C
?
C
X
Y
Full Adders

He aquí el full adder
Full Adders

Ejercicio: diseñar un sumador de cuatro bits
usando half y/o full adders.
(Gp:) Ae
(Gp:) B
(Gp:) ?
(Gp:) As
(Gp:) Full
Adder
(Gp:) A
(Gp:) A
(Gp:) B
(Gp:) ?
(Gp:) As
(Gp:) Half
Adder
A4 A3 A2 A1
B4 B3 B2 B1
+
C5 C4 C3 C2 C1
Adders

(Gp:) A4 A3 A2 A1
(Gp:) B4 B3 B2 B1
(Gp:) +
(Gp:) C5 C4 C3 C2 C1
(Gp:) A1
(Gp:) B1
(Gp:) ?
(Gp:) As
(Gp:) HA
(Gp:) ?
(Gp:) As
(Gp:) FA
(Gp:) ?
(Gp:) As
(Gp:) FA
(Gp:) Ae
(Gp:) ?
(Gp:) As
(Gp:) FA
(Gp:) Ae
(Gp:) Ae
(Gp:) A2
(Gp:) B2
(Gp:) A3
(Gp:) B3
(Gp:) A4
(Gp:) B4
(Gp:) C1
(Gp:) C2
(Gp:) C3
(Gp:) C4
(Gp:) C5
Sumador de cuatro bits:
Adders

Decodificadores
Decodificadores de n entradas pueden seleccionar una de 2n salidas
Son muy importantes, por ejemplo:
Seleccionar una locación en una memoria a partir de una dirección colocada en el bus memoria

Decodificadores – Ejemplo
Decodificador 2-a-4
Si x = 0 e y = 1, que línea de salida queda habilitada?

Selecciona una salida de varias entradas
La entrada que es seleccionada como salida es determinada por las líneas de control
Para seleccionar entre n entradas, se necesitan log2n líneas de control.
Multiplexores
Demultiplexor
Exactamente lo contrario
Dada una entrada la direcciona entre n salidas, usando log2n líneas de control.

Así luce un multiplexor 4-a-1
Si S0 = 1 y S1 = 0, que entrada es transferida a la salida?
Multiplexor – Ejemplo

Función Mayoría

Ejercicio: Implementar la función Mayoría con un Multiplexor

Ejercicio: Implementar la función Mayoría con un Multiplexor

Ejercicio
Construir una ALU de 1 bit
3 entradas:
A, B, Carry
Cuatro operaciones:
A.B, A+B, NOT B, Suma(A,B,Carry)
Salidas
Resultado, CarryOut

Alu de 1bit
Decoder
Full Adder

Alu de 1bit

Un ALU de 8 bits


ROM usando un decoder

Links
Libro Tanenbaum
Demo compuertas: http://www.play-hookey.com/digital/derived_gates.html
Para ver Compuertas logicas en detalle: http://www.csc.sdstate.edu/%7egamradtk/csc317/csc317notes.html