
INTRODUCCIÓN PRIMER PRINCIPIO: Conservación de la
energía. La experiencia demuestra que no todas las
transformaciones energéticas permitidas por el primer
principio ocurren en la naturaleza. Es necesario formular un
segundo principio de la Termodinámica que nos informe
acerca de los procesos que son posibles en la naturaleza y los
que no lo son. El segundo principio admite diversas formulaciones
diferentes, todas ellas equivalentes. El estudio se aborda desde
el punto de vista más afín a la ingeniería:
las máquinas térmicas.

PROCESO PERMITIDO El bloque se mueve sobre la superficie
deteniéndose después de cierto tiempo. El trabajo
realizado se transforma en energía interna. Bloque y
superficie se calientan. El sistema cede energía interna
en forma de calor al medio ambiente hasta lograr el equilibrio.
RESULTADO: el trabajo mecánico se ha transformado
íntegramente en calor cedido al entorno. PROCESO NO
PERMITIDO El bloque disminuye su energía interna, el
bloque se enfría. La energía interna se transforma
en energía cinética. El bloque se mueve. El sistema
absorbe calor del medio ambiente hasta regresar al estado de
equilibrio térmico. RESULTADO: El calor tomado del medio
ambiente se ha transformado totalmente en trabajo. AMBOS PROCESOS
SON COHERENTES CON EL PRIMER PRINCIPIO NECESIDAD DEL SEGUNDO
PRINCIPIO SISTEMA: Un bloque de masa m sobre una superficie con
fricción

NECESIDAD DEL SEGUNDO PRINCIPIO SISTEMA: Un cuerpo caliente en
contacto con otro más frío PROCESO PERMITIDO El
cuerpo caliente cede parte de su energía interna, en forma
de calor, al cuerpo más frío. PROCESO NO PERMITIDO
El cuerpo más frío cede parte de su energía
interna, en forma de calor, al cuerpo caliente. NUEVAMENTE AMBOS
PROCESOS SON COHERENTES CON EL PRIMER PRINCIPIO, PERO SOLAMENTE
UNO DE ELLOS ES “ NATURAL”. LA FALTA DE
SIMETRÍA EN LOS ROLES DEL CALOR Y TRABAJO COMO FORMAS DE
TRANSFERENCIA DE ENERGÍA Y LA EXISTENCIA DE UNA
DIRECCIÓN “PRIVILEGIADA” PARA LOS PROCESOS
NATURALES NO SE INFIEREN DEL PRIMER PRINCIPIO DE LA
TERMODINÁMICA

MÁQUINAS TÉRMICAS La Termodinámica nace de
las máquinas térmicas. Máquina
térmica: dispositivo que transforma energía interna
en otra forma de energía útil. En general se dice
que transforma calor en trabajo

MÁQUINAS TÉRMICAS UNA MÁQUINA TÉRMICA
CONDUCE UNA SUSTANCIA DE TRABAJO A TRAVÉS DE UN PROCESO
CÍCLICO SE EXTRAE ENERGÍA DE UN FOCO A MAYOR
TEMPERATURA QC SE OBTIENE TRABAJO W LA MÁQUINA CEDE
ENERGÍA A UN FOCO TÉRMICO A MENOR TEMPERATURA
Qf

Primer principio aplicado al proceso cíclico que realiza
la máquina: ?U = Q – W donde Q = QC – lQf| Proceso
cíclico ?U = 0 Por tanto: W = Qc – lQf| EL TRABAJO
REALIZADO POR UNA MÁQUINA TÉRMICA ES IGUAL A LA
ENERGÍA NETA ABSORBIDA POR LA MÁQUINA

MÁQUINAS TÉRMICAS. CARACTERÍSTICAS Y ESQUEMA
DE PRESENTACIÓN ENUNCIADO DE KELVIN – PLANK ES IMPOSIBLE
CONSTRUIR UNA MÁQUINA TÉRMICA QUE, OPERANDO EN UN
CICLO, NO PRODUZCA OTRO EFECTO QUE TRANSFERIR ENERGÍA
TÉRMICA CONTINUAMENTE DE UN FOCO CALIENTE A UN FOCO
FRÍO Rendimiento. ? = w/Qc

MOTOR DE CUATRO TIEMPOS

CICLO OTTO P c ADIABÁTICA d Qc b Qf a ADIABÁTICA vb
va v La mezcla de aire-gasolina entre al cilindro en el punto a
La compresión a b es adiabática, es decir, no hay
transferencia de calor La combustión de los gases
está representada por la entrada de calor Qh que eleva la
temperatura a volumen constante El tiempo donde se realiza
trabajo o fase de potencia , corresponde a la expansión
adiabática c d. Durante el escape, corresponde al proceso
d a, donde se elimina calor Qc al foco frío.

Rendimiento de Ciclo Otto Proceso a b: Compresión
Adiabática TaVa?-1 = TbVb?-1 ; Q = 0 Proceso b c: Isocoro
Entrada de calor QC al sistema QC = Cv(Tc – Tb) Proceso c
d: Expansión Adiabática TcVc?-1 = TdVd?-1 ; Q = 0
Proceso d a: Isocoro Salida de calor QF del sistema QF = Cv(Ta
– Td) Rendimiento = 1 – (Vb/Va)?-1

SEGUNDO PRINCIPIO DE LA TERMODINÁMICA ENUNCIADO DE
CLAUSIUS ES IMPOSIBLE CONSTRUIR UNA MÁQUINA TÉRMICA
QUE, OPERANDO EN UN CICLO, NO PRODUZCA OTRO EFECTO QUE TRANSFERIR
ENERGÍA TÉRMICA CONTINUAMENTE DE UN FOCO
FRÍO A UN FOCO CALIENTE EFICACIA ? = QC/W

EQUIVALENCIA DE LOS ENUNCIADOS DE KELVIN Y DE CLAUSIUS

EQUIVALENCIA DE LOS ENUNCIADOS DE KELVIN Y DE CLAUSIUS

REFRIGERADORES REFRIGERADOR: Máquina compuesta de un
fluido refrigerante que es forzado a recorrer un circuito
cerrado, un compresor, un condensador, un tubo capilar
(válvula de expansión) y un evaporador. FLUIDO
REFRIGERANTE: baja temperatura de vaporización y baja
presión de condensación a temperatura ambiental.
COMPRESOR: máquina de succión accionada por un
motor eléctrico. Extrae fluido de una rama, bajando su
presión y lo inyecta en otra rama aumentando su
presión. Impulsa al fluido refrigerante a lo largo del
circuito

CONDENSADOR: formado por un tubo largo en forma de
serpentín. Localizado en la parte posterior del
refrigerador. A la salida del compresor el fluido presenta estado
gaseoso y debido a la presión y a la pérdida de
energía con el medio ambiente pasa a estado
líquido. TUBO CAPILAR: tubo de diámetro interno de
medio milímetro. El fluido que entra al tubo capilar en
forma líquida al salir se expande rápidamente
pasando al estado gaseoso. Expansión que ocurre en el
evaporador.

EVAPORADOR: Formado por un tubo en forma de serpentín
acoplado al congelador. Para pasar al estado gaseoso el fluido
refrigerante absorbe calor del congelador. Al salir del
evaporador el fluido llega al compresor y el ciclo comienza de
nuevo.




p(atm) 30 B C isoterma D adiabática 1.5 A v 2v v(L) Gas
ideal: cv= 3R/2 EJEMPLO.- Una máquina térmica
trabaja sobre tres moles de un gas monoatómico, realizando
el ciclo ABCD mostrado en la figura. El volumen en el estado C es
el doble del volumen en el estado B y TA= 20 ºC.

RENDIMIENTO DEL CICLO Qabs= 1125 atm?l Qced= 608 atm?l W= 516
atm?l ? = 46 %

EJEMPLO.- Un refrigerador trabaja según el ciclo ABC
mostrado en la figura. La sustancia de trabajo es un mol de gas
ideal diatómico P(atm) p C adiabática 1.3 A B 16 24
v(l) gas diatómico cv = 5R/2

COEFICIENTE DE EFICACIA DEL CICLO. W = 3.6 atm?l (trabajo sobre
el sistema) Q = 36.2 atm?l ( absorbido por el sistema) ? =
10

CONDICIONES DE REVERSIBILIDAD No debe realizarse trabajo por
rozamiento, fuerzas viscosas u otras fuerzas disipativas que
producen calor. No puede existir conducción de calor
debido a una diferencia de temperatura finita. El proceso debe
ser cuasiestático, de modo que el sistema se encuentre
siempre en un estado de equilibrio. Todo proceso que viole alguna
de las condiciones anteriores es irreversible. PROCESOS
REVERSIBLES

Máquina de Carnot La máquina de Carnot es una
máquina que trabaja cíclicamente entre dos focos
térmicos. La sustancia de trabajo sufre un proceso
cíclico reversible absorbiendo calor del foco caliente y
cediéndolo al foco frío. La reversibilidad del
proceso exige que la absorción y la cesión de calor
de los focos se produzca con la sustancia de trabajo a la misma
temperatura que los focos. Procesos isotermos reversibles. La
forma más sencilla de conectar los procesos isotermos en
ambos focos es mediante dos procesos adiabáticos
reversibles.
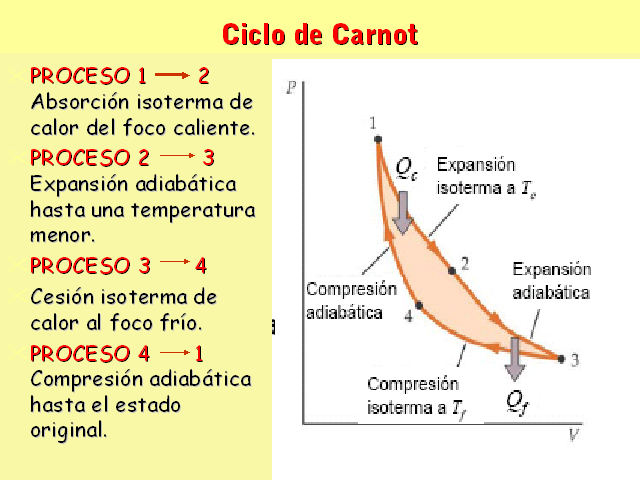
Ciclo de Carnot PROCESO 1 2 Absorción isoterma de calor
del foco caliente. PROCESO 2 3 Expansión adiabática
hasta una temperatura menor. PROCESO 3 4 Cesión isoterma
de calor al foco frío. PROCESO 4 1 Compresión
adiabática hasta el estado original.

Representación esquemática del ciclo de
Carnot

Teorema de Sadi Carnot Establecido por Sadi Carnot en 1824, antes
de que se enunciaran el primer y segundo principios de la
termodinámica. Constituye otra forma de enunciar el
segundo principio de la termodinámica. Ninguna
máquina térmica que funcione entre dos focos
térmicos puede tener un rendimiento mayor que una
máquina térmica reversible (máquina de
Carnot) que opere entre esos mismos focos
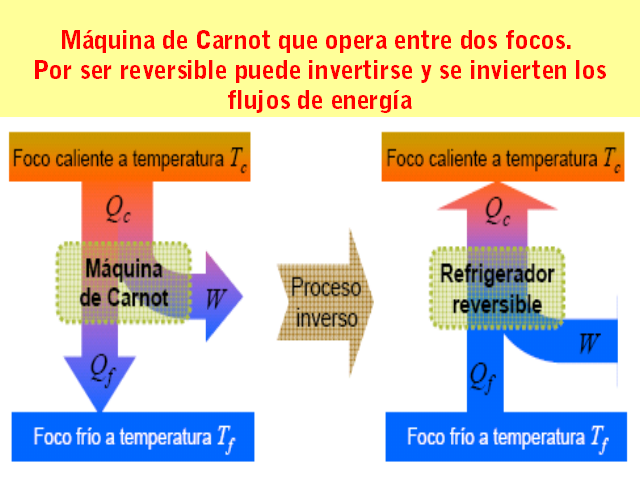
Máquina de Carnot que opera entre dos focos. Por ser
reversible puede invertirse y se invierten los flujos de
energía
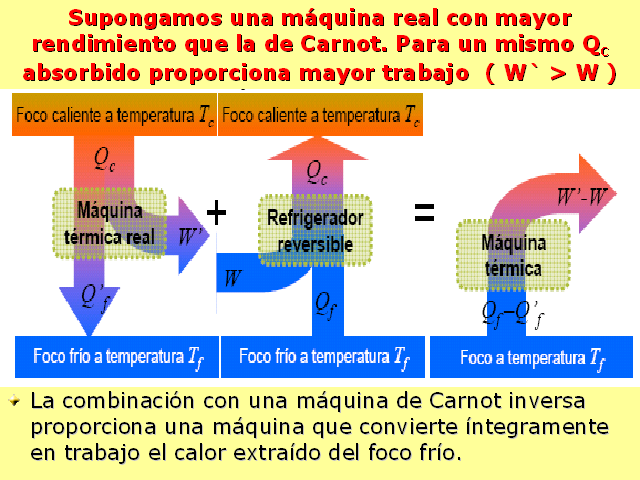
La combinación con una máquina de Carnot inversa
proporciona una máquina que convierte íntegramente
en trabajo el calor extraído del foco frío.
Supongamos una máquina real con mayor rendimiento que la
de Carnot. Para un mismo QC absorbido proporciona mayor trabajo (
W` > W )

Rendimiento de un ciclo de Carnot


Conclusiones El rendimiento de cualquier máquina de Carnot
que opere entre dos focos dados es el mismo. No depende de la
sustancia de trabajo. Solamente depende de la temperatura de los
focos. El segundo principio prohíbe un rendimiento igual a
1. Por lo tanto el máximo rendimiento de una
máquina no es 1, sino que viene dado por el rendimiento de
una máquina de Carnot que opere entre esos focos.
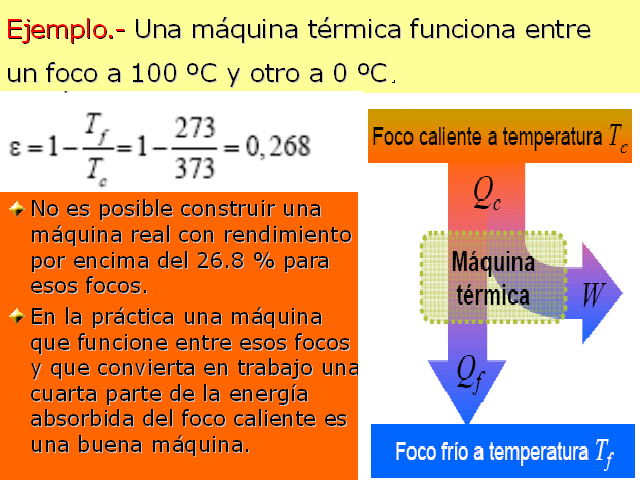
No es posible construir una máquina real con rendimiento
por encima del 26.8 % para esos focos. En la práctica una
máquina que funcione entre esos focos y que convierta en
trabajo una cuarta parte de la energía absorbida del foco
caliente es una buena máquina. Ejemplo.- Una
máquina térmica funciona entreun foco a 100 ºC
y otro a 0 ºC.

Ejemplo.- Una máquina frigorífica funciona entre un
foco a 100º C y otro a 0º C. Determinar su
máximo rendimiento teórico