
Introducción ¿Qué es Matlab?, MATrix
LABoratory Es un lenguaje de programación (inicialmente
escrito en C) para realizar cálculos numéricos con
vectores y matrices. Como caso particular puede también
trabajar con números escalares, tanto reales como
complejos. Cuenta con paquetes de funciones especializadas

Introducción Elementos básicos del escritorio de
Matlab Command Windows: Donde se ejecutan todas las instrucciones
y programas. Se escribe la instrucción o el nombre del
programa y se da a Enter. Command History: Muestra los
últimos comandos ejecutados en Command Windows. Se puede
recuperar el comando haciendo doble Current directory: Situarse
en el directorio donde se va a trabajar Help (también se
puede usar desde comand windows) Workspace: Para ver las
variables que se están usando y sus dimensiones (si son
matrices) Editor del Matlab: Todos los ficheros de comandos
Matlab deben de llevar la extensión .m
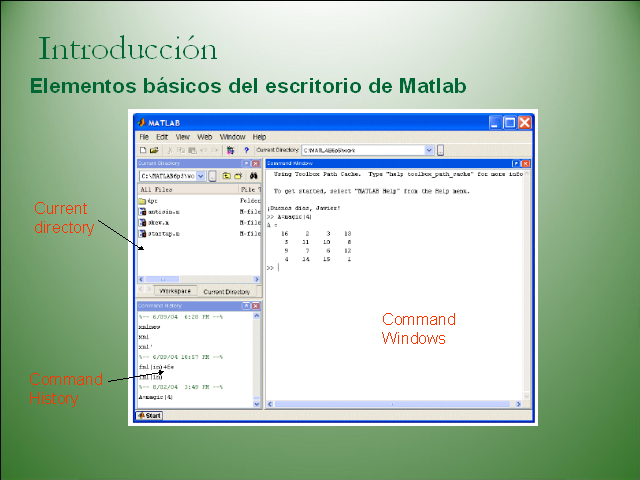
Introducción Elementos básicos del escritorio de
Matlab Command Windows Current directory Command History

Introducción Elementos básicos del escritorio de
Matlab Abrir el matlab. Usar View para sacar las ventanas que
hagan falta. Comand Windows: Donde se ejecutan todas las
instrucciones y programas. Se escribe la instrucción o el
nombre del programa y se da a Enter. Hacer ejemplo en
línea de comandos: x=2*3, y mirar en workspace la variable
x Current directory: Situarse en el directorio donde se va a
trabajar Help (también se puede usar desde comand windows)
(índice, search, DEMOS). Workspace: Para ver las variables
que se están usando Editor del Matlab: Todos los ficheros
de comandos Matlab deben de llevar la extensión .m En
current directoy crear un fichero nuevo main_prueba.m, decirles
lo de main. Correr el programa main_prueba.

Introducción Algunos comentarios sobre la ventana de
comandos Se pueden recuperar instrucciones con las teclas ?? Se
puede mover por la línea de comandos con las teclas ? ?.
Ir al comienzo de la línea con la tecla Inicio y al final
con Fin. Con Esc se borra toda la línea. Se puede cortar
la ejecución de un programa con Ctrl+C

Introducción Debugger Set/Clear breakingpoint: Coloca o
borra un punto de ruptura en la línea en que está
colocado el cursor Clear all breakingpoints:: Borra todos los
puntos de ruptura Step: Avanza un paso en el programa Step in:
Avanza un paso en el programa y si en ese paso se llama a una
función, entra en dicha función Step out: Avanza un
paso en el programa y si en ese paso se llama a una
función, entra en dicha función Continue: Continua
ejecutando hasta el siguiente punto de ruptura Quit debugging:
Termina la ejecución del debugger

Números y operaciones Datos numéricos: No hace
falta definir variables enteras, reales, etc. como en otros
lenguajes Números enteros: a=2 Números reales:
x=-35.2 Máximo de 19 cifras significativas
2.23e-3=2.23*10-3 Precisión y formatos: Por defecto tiene
un formato corto, pero se pueden usar otros >> format long
(14 cifras significativas) >> format short (5 cifras
significativas) >> format short e (notación
exponencial) >> format long e (notación exponencial)
>> format rat (aproximación racional) Ver en
menú de File: Preferences ? Command Windows

Preferences (en el menú de File)

Números y operaciones Datos numéricos: Son
sensibles a las mayúsculas: x=5, X=7 Información
sobre variables que se están usando y sus dimensiones (si
son matrices): Workspace. También tecleando >> who
>> whos (da más información) Para eliminar
alguna variable se ejecuta >> clear variable1 variable2 Si
se quieren borrar todas las variables: >> clear Constantes
características: pi=?, NaN (not a number, 0/0), Inf=?.
Números complejos: i=sqrt(-1) (sólo se puede usar i
o j), z=2+i*4, z=2+4i Cuidado con no usar luego ‘i’
como contador en un bucle trabajando con complejos.

Números y operaciones Operaciones aritméticas
elementales: Suma: +, Resta – Multiplicación: *,
División: / Potencias: ^ Orden de prioridad: Potencias,
divisiones y multiplicaciones y por último sumas y restas.
Usar () para cambiar la prioridad Ejemplo:
main_operaciones_numeros.m. Probar el Debugger

Introducción Debugger Set/Clear breakingpoint: Coloca o
borra un punto de ruptura en la línea en que está
colocado el cursor Clear all breakingpoints:: Borra todos los
puntos de ruptura Step: Avanza un paso en el programa Step in:
Avanza un paso en el programa y si en ese paso se llama a una
función, entra en dicha función Step out: Avanza un
paso en el programa y si en ese paso se llama a una
función, entra en dicha función Continue: Continua
ejecutando hasta el siguiente punto de ruptura Quit debugging:
Termina la ejecución del debugger

Números y operaciones Operaciones aritméticas
elementales: Ejemplo: main_operaciones_numeros.m
Instrucción clear. Funcionamiento de Debugger: run,
breakpoint, step Evaluar una línea. Cometer un error de
programación para que el Debugger te dé la
línea. Comentarios sobre el editor: ‘;’ para
que no escriba, % para comentar líneas,
‘…’ para continuar una linea No se pueden
dejar espacios en blanco en el nombre de un fichero

Números y operaciones Funciones de Matlab: exp(x), log(x),
log2(x) (en base 2), log10(x) (en base 10), sqrt(x) Funciones
trigonométricas: sin(x), cos(x), tan(x), asin(x), acos(x),
atan(x), atan2(x) (entre –pi y pi) Funciones
hiperbólicas: sinh(x), cosh(x), tanh(x), asinh(x),
acosh(x), atanh(x) Otras funciones: abs(x) (valor absoluto),
int(x) (parte entera), round(x) (redondea al entero más
próximo), sign(x) (función signo) Funciones para
números complejos: real(z) (parte real), imag(z) (parte
imaginaria), abs(z) (módulo), angle(z) (ángulo),
conj(z) (conjugado) Ejemplo: main_operaciones_numeros.m

Vectores y matrices Definición de vectores: Vectores fila;
elementos separados por blancos o comas >> v =[2 3 4]
Vectores columna: elementos separados por punto y coma (;)
>> w =[2;3;4;7;9;8] Dimensión de un vector w:
length(w) Generación de vectores fila: Especificando el
incremento h de sus componentes v=a:h:b Especificando su
dimensión n: linspace(a,b,n) (por defecto n=100)
Componentes logarítmicamente espaciadas logspace(a,b,n) (n
puntos logarítmicamente espaciados entre 10a y 10b. Por
defecto n=50) Ejemplo: main_operaciones_matrices.m

Vectores y matrices Definición de matrices: No hace falta
establecer de antemano su tamaño (se puede definir un
tamaño y cambiarlo posteriormente). Las matrices se
definen por filas; los elementos de una misma fila están
separados por blancos o comas. Las filas están separadas
por punto y coma (;). » M=[3 4 5; 6 7 8; 1 -1 0] Matriz
vacía: M=[ ]; Información de un elemento: M(1,3),
de una fila M(2,:), de una columna M(:,3). Cambiar el valor de
algún elemento: M(2,3)=1; Eliminar una columna: M(:,1)=[
], una fila: M(2,:)=[ ]; Ejemplo:
main_operaciones_matrices.m

Vectores y matrices Definición de matrices:
Generación de matrices: Generación de una matriz de
ceros, zeros(n,m) Generación de una matriz de unos,
ones(n,m) Inicialización de una matriz identidad eye(n,m)
Generación de una matriz de elementos aleatorios rand(n,m)
Añadir matrices: [X Y] columnas, [X; Y] filas Ejemplo:
main_operaciones_matrices.m

Operaciones con vectores y matrices Operaciones de vectores y
matrices con escalares: v: vector, k: escalar: v+k adición
o suma v-k sustracción o resta v*k multiplicación
v/k divide cada elemento de v por k k./v divide k por cada
elemento de v v.^k potenciación de cada componente de v a
k k.^v potenciación k elevado a cada componente de v
Ejemplo: main_operaciones_matrices.m

Operaciones con vectores y matrices Operaciones con vectores y
matrices: + adición o suma – sustracción o
resta * multiplicación matricial .* producto elemento a
elemento ^ potenciación .^ elevar a una potencia elemento
a elemento división-izquierda / división-derecha
./ y . división elemento a elemento matriz traspuesta:
B=A’ (en complejos calcula la traspuesta conjugada,
sólo la traspuesta es B=A.’) Ejemplo:
main_operaciones_matrices.m

Funciones para vectores y matrices Funciones de matlab para
vectores y matrices: sum(v) suma los elementos de un vector
prod(v) producto de los elementos de un vector dot(v,w) producto
escalar de vectores cross(v,w) producto vectorial de vectores
mean(v) (hace la media) diff(v) (vector cuyos elementos son la
resta de los elemento de v) [y,k]=max(v) valor máximo de
las componentes de un vector (k indica la posición),
min(v) (valor mínimo). El valor máximo de una
matriz M se obtendría como max(max(M)) y el mínimo
min(min(v)) Aplicadas algunas de estas funciones a matrices,
realizan dichas operaciones por columnas.

Funciones para vectores y matrices Funciones de Matlab para
vectores y matrices [n,m]=size(M) te da el número de filas
y columnas matriz inversa: B=inv(M), rango: rank(M) diag(M):
Obtencion de la diagonal de una matriz. sum(diag(M)) calcula la
traza de la matriz A. diag(M,k) busca la k-ésima diagonal.
norm(M) norma de una matriz (máximo de los valores
absolutos de los elementos de A) flipud(M) reordena la matriz,
haciendo la simétrica respecto de un eje horizontal.
fliplr(M) ) reordena la matriz, haciendo la simétrica
respecto de un eje vertical [V, landa]=eig(M) da una matriz
diagonal landa con los autovalores y otra V cuyas columnas son
los autovectores de M Ejemplo: main_operaciones_matrices.m

Funciones para vectores y matrices Guardar en ficheros y
recuperar datos: save nombre_fichero nombre_matriz1,
nombre_matriz2 load nombre_fichero nombre_matriz1, nombre_matriz2
save nombre_fichero nombre_matriz1 –ascii (guarda 8 cifras
decimales) save nombre_fichero nombre_matriz1 –ascii
–double (guarda 16 cifras decimales) Ejemplo:
main_operaciones_matrices.m

Polinomios Los polinomios se representan en Matlab por un vector
fila de dimensión n+1 siendo n el grado del polinomio.
Ejemplo: x3+2x-7 se representa por >> pol1=[1 0 2 -7]
Cálculo de las raíces: roots (da un vector columna,
aunque pol1 es un vector fila) >>raices=roots(pol1) Un
polinomio puede ser reconstruido a partir de sus raíces
con el comando poly >> p=poly(raices) (da un vector fila)
** Si el argumento de poly es una matriz se obtiene el polinomio
característico de la matriz.

Polinomios Funciones de Matlab para polinomios Calcular el valor
de un polinomio p en un punto dado x: polyval
>>y=polyval(p,x) Multiplicar y dividir polinomios:
conv(p,q) y deconv(p,q) Calcular el polinomio derivada:
polyder(p)

Gráficos 2D y 3D Funciones gráficas 2D y 3D
elementales 2D: plot() crea un gráfico a partir de
vectores con escalas lineales sobre ambos ejes, >>
plot(X,Y,’opción’) (opción: permite
elegir color y trazo de la curva) hold on: permite pintar
más gráficos en la misma figura (se desactiva con
hold off) grid activa una cuadrícula en el dibujo.
Escribiendo de nuevo grid se desactiva. 2D: loglog() escala
logarítmica en ambos ejes, semilogx(): escala lineal en el
eje de ordenadas y logarítmica en el eje de abscisas,
semilogy(): escala lineal en abscisas y logarítmica en
ordenadas Ejemplo: main_dibujos.m, y ver en Demos: Graphics

Gráficos 2D y 3D Funciones gráficas 2D y 3D
elementales 2D: subplot(n,m,k) subdivide una ventana
gráfica se puede en m particiones horizontales y n
verticales y k es la subdivisión que se activa. 2D:
polar(ángulo,r) para pintar en polares 2D:
fill(x,y,’opción’) dibuja una curva cerrada y
la rellena del color que se indique en
‘opción’ 3D: plot3 es análoga a su
homóloga bidimensional plot. » plot3(X,Y,Z,
’opción’)

Gráficos 2D y 3D Funciones gráficas 2D y 3D
elementales Ejemplo: main_dibujos.m, y ver en Demos: Graphics.
Usar en Help: Search para plot, para ver los tipos de
línea. Editor de la ventana gráfica.

Gráficos 2D y 3D Elección de la escala de los ejes
axis([x0 x1 y0 y1]) (2D), axis([x0 x1 y0 y1 z0 z1]) (3D) axis
auto: devuelve la escala a la de defecto axis off: desactiva los
etiquetados de los ejes desapareciendo los ejes, sus etiquetas y
la malla, axis on: lo activa de nuevo axis equal: los mismos
factores de escala para los dos ejes axis square: cierra con un
cuadrado la región delimitada por los ejes de coordenadas
actuales. Para elegir las etiquetas que aparecen en los ejes:
set(gca, ‘XTick’,-pi:pi/2,pi) %gca:get current axis
set(gca,
‘XTicklabel’,({‘-pi’,’-pi/2’,0,’pi/2’,’pi’})

Gráficos 2D y 3D Funciones para añadir
títulos a la gráfica title('título')
añade un título al dibujo. Para incluir en el texto
el valor de una variable numérica es preciso transformarla
mediante : int2str(n) convierte el valor de la variable entera n
en carácter num2str(x) convierte el valor de la variable
real o compleja x en carácter. Ejemplo: title(num2str(x))
xlabel(‘texto’) añade una etiqueta al eje de
abscisas. Con xlabel off desaparece. Lo mismo
ylabel(‘texto’) o zlabel(‘texto’)
text(x,y,'texto') introduce 'texto' en el lugar especificado por
las coordenadas x e y. Si x e y son vectores, el texto se repite
por cada par de elementos. gtext('texto') introduce texto con
ayuda del ratón.

Gráficos 2D y 3D Funciones de Matlab para gráficos
2D y 3D Imprimir gráficos: Print (botón File en
ventana gráfica) Guardar gráficos: Save
(botón File en ventana gráfica): Se crea un fichero
.fig que podrá volver a editarse y modificarse Exportar
gráficos: Export (botón File en ventana
gráfica) figure(n): Llamar una nueva figura o referirnos a
una figura ya hecha close all borra todas las figuras,
close(figure(n)) una en concreto

Ejercicio I Representar las funciones: y1= sin(3 p x)/ex
y2=cos(3p x)/ex con x variando entre 0 y 3 p,obteniendo una
única figura de la forma:

Ejercicio II Obtener la solución del sistema de
ecuaciones: 3x+2y-z=1 5x+y+3z=-2 3y-4z=3 Sea A de coeficientes
del sistema anterior. Calcular el máximo autovalor de A y
su autovector asociado como salida del programa

Gráficos 2D y 3D Representación gráfica de
superficies Creación de una malla a partir de vectores [X,
Y]=meshgrid(x,y) Gráfica de la malla construida sobre la
superficie Z(X,Y): mesh(X,Y,Z), meshc(X,Y,Z) (dibuja
además líneas de nivel en el plano z=0)
Gráfica de la superficie Z(X,Y): surf(X,Y,Z), surfc(X,Y,Z)
pcolor(Z) dibuja proyección con sombras de color sobre el
plano (la gama de colores está en consonancia con las
variaciones de Z) contour(X,Y,Z,v) y contour3(X,Y,Z,v) generan
las líneas de nivel de una superficie para los valores
dados en v. Para etiquetar las líneas, primero
cs=contour(Z) (para saber los valores del contorno) y luego
clabel(cs) o directamente clabel(cs,v) Ejemplo:
main_dibujo_superficie.m y ver en Demos: Graphics

Gráficos 2D y 3D Representación gráfica de
superficies Diferentes formas de representar los polígonos
coloreados: shading flat: sombrea con color constante para cada
polígono. shading interp: sombrea calculado por
interpolación de colores entre los vértices de cada
polígono shading faceted: sombreado constante con
líneas negras superpuestas (opción por defecto)
hidden off (desactiva la desaparición de líneas
escondidas), hidden on (lo activa) Manipulación de
gráficos view(azimut, elev), view([xd,yd,zd])
rotate(h,d,a) o rotate(h,d,a,o), ‘h’ es el objeto,
‘d’ es un vector que indica la dirección,
‘a’ un ángulo y ‘o’ el origen de
rotación En ventana gráfica: View (camera
toolbar)

Gráficos 2D y 3D Transformación de coordenadas
[ang,rad]=cart2pol(x,y), de cartesianas a polares
[ang,rad,z]=cart2pol(x,y,z), de cartesianas a cilindricas
[x,y]=pol2cart(ang,rad), de polares a cartesianas
[x,y,z]=pol2cart(ang,rad,z), de cilindricas a cartesianas
[angx,angz,rad]=cart2sph(x,y,z), de cartesianas a esfericas
[x,y,z]=aph2cart(angx,angz,rad), de esfericas a cartesianas

Gráficos 2D y 3D Creación de películas Una
película se compone de varias imágenes (frames)
getframe se emplea para guardar todas esas imágenes.
Devuelve un vector columna con la información necesaria
para reproducir la imagen que se acaba de representar, por
ejemplo con la función plot. Esos vectores se almacenan en
una matriz M. movie(M,n,fps) representa n veces la
película almacenada en M a una velocidad de fps
imágenes por segundo X=0:0.01:2*pi; for j=1:10
plot(x,sin(j*x)/2) M(j)=getframe; end movie(M,4,6) Ejemplo:
main_pelicula.m

Programación Ficheros de Matlab Ficheros de programa: Se
construyen mediante una secuencia de comandos. El fichero
principal se llamará main_nombre.m Ficheros de
función: para crear funciones propias. Son llamados por
los ficheros de programa. La primera línea es ejecutable y
empieza por la palabra function de la forma: function
arg_salida=funcion_nombre(arg_entrada, parametros) El fichero se
debe guardar como funcion_nombre.m Comandos de entrada y salida:
input: permite introducir datos: ae=input(‘Teclee valor de
a’); disp: muestra un texto por pantalla: disp(‘El
algoritmo no ha convergido’) Ejemplo:
main_pintarseno.m

Programación Ficheros de Matlab Ficheros de programa: Se
construyen mediante una secuencia de comandos. El fichero
principal se llamará main_nombre.m Ficheros de
función: para crear funciones propias. Son llamados por
los ficheros de programa. La primera línea es ejecutable y
empieza por la palabra function de la forma: function
arg_salida=funcion_nombre(arg_entrada, parametros) El fichero se
debe guardar como funcion_nombre.m Comandos de entrada y salida:
input: permite introducir datos: ae=input(‘Teclee valor de
a’); disp: muestra un texto por pantalla: disp(‘El
algoritmo no ha convergido’) Ejemplo: main_pintarseno.m.
Usar el Debugger para meterse en la función

Programación Funciones de funciones
fzero(‘nombre_funcion’,x0): Calcula el cero de una
función más próximo al valor de la variable
x0 fminsearch(‘funcion’,x0): calcula el mínimo
relativo de una función más próximo a x0
fminbnd(‘funcion‘,a,b): calcula un mínimo de
la función en el intervalo [a,b]

Programación Funciones de funciones
fzero(‘nombre_funcion’,x0): Calcula el cero de una
función más próximo al valor de la variable
x0 fminsearch(‘funcion’,x0): calcula el mínimo
relativo de una función más próximo a x0
fminbnd(‘funcion‘,a,b): calcula un mínimo de
la función en el intervalo [a,b] Ejemplo de fzero en
main_pintarseno

Programación Bucles for k=n1:incre:n2 end for
k=vector_columna end while end Ejemplo: main_bucles

Programación Bucles for k=n1:incre:n2 end for
k=vector_columna end while end Ejemplo: main_bucles. Ver
cómo ir rellenando una matriz.

Programación Estructuras de control condicionadas
Operaciones lógicas: >, <, >=,<=,== (igual) |
(or), &(and) ~ (no), ~= (no igual) Ejemplo: main_condicional
if end if else end if elseif else end

Programación Interpolación 1D: Se define un
polinomio de un cierto grado (ejemplo, n=2, ax^2+bx+c), para
hacer la interpolación: p=polyfit(x,y,n). Si se quiere la
interpolación en ciertos valores ’xi’:
yi=polyval(p,xi). yi = interp1(x,Y,xi,metodo). Métodos:
‘linear’ (interpolación lineal),
’cubic’ (cúbica), ’spline (spline
cúbica) 2D:
matriz_Z=interp2(X,Y,Z,matriz_X,matriz_Y,metodo). Métodos:
’bilinear’ (interpolación lineal),
’bicubic’ (cúbica)

Análisis numérico Integración 1D: quad,
quadl: integran una función en un intervalo [a,b]
quad(‘funcion’,a,b) 2D: dblquad: integran una
función en un intervalo [xmin,xmax]x[ymin,ymax]
dblquad('y*sin(x)+x*cos(y)',xmin,xmax,ymin,ymax)

Análisis numérico Resolución de ecuaciones
diferenciales Resolución de problemas de valores iniciales
para ecuaciones diferenciales ordinarias (ODEs)
[T,Y]=solver(‘F’,tspan,Y0) solver: algoritmo de
resolución de ODEs, ode45, ode23, ode113, ode15s,ode23s.
F: función que contiene las ecuaciones diferenciales en
forma matricial Tspan: vector de tiempos [t0 tfinal] de
integración. Y0: vector columna de condiciones iniciales
en t0