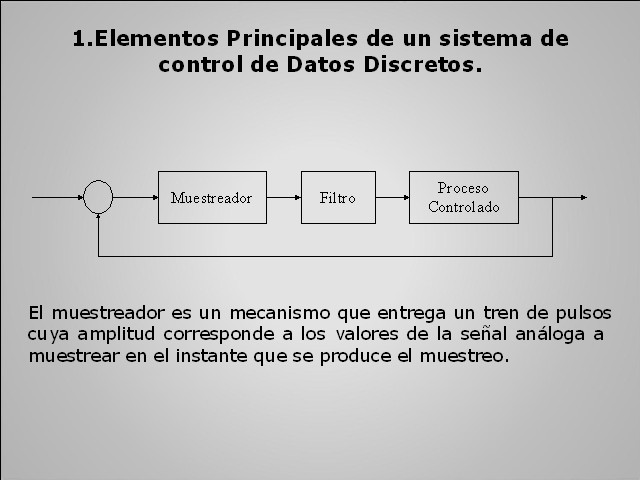
Elementos Principales de un sistema de control de Datos
Discretos. El muestreador es un mecanismo que entrega un tren de
pulsos cuya amplitud corresponde a los valores de la señal
análoga a muestrear en el instante que se produce el
muestreo. (Gp:) Muestreador (Gp:) Filtro (Gp:) Proceso
Controlado
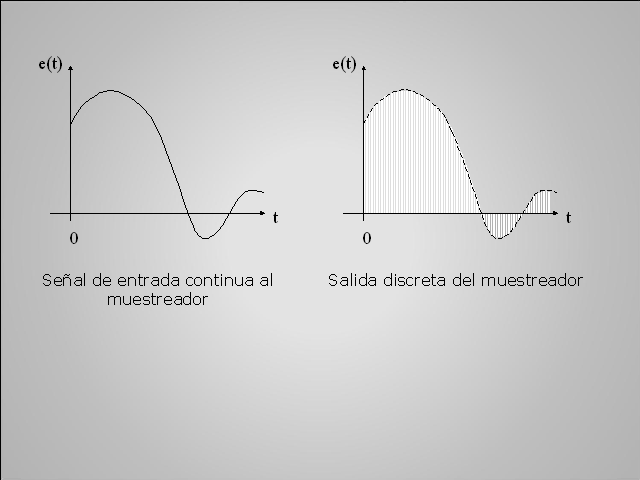
Señal de entrada continua al muestreador t 0 e(t) t 0 e(t)
Salida discreta del muestreador

Ejemplo de Sistema de Control Digital Prefiltro Proceso
Controlado A/D Control Digital DA + – + – Control
automático para un eje para el pilotaje automático
de un avión. Giroscopio Transduct. Posición Comando
Altitud

Prefiltro Proceso Controlado A/D Control Digital DA + – Sistema
con muestreo múltiple Los muestreadores adquieren muestras
de la señal con frecuencia constante, se cumple un periodo
de muestreo. Los retenedores mantienen el valor de la
señal retenida hasta que llega un nuevo valor
correspondiente a una nueva muestra. Giroscopio TX
Posición Retenedor Retenedor Comando Altitud

La Bucla Típica de Control Realimentada Computador Digital
Actuador DA + – Sensor A / D Reloj Planta Proceso

Tratamiento (Data Login): Recoger la máxima
información sobre el funcionamiento del proceso.
Medición de variables y parámetros. Pretratamiento:
– Normalizar – Convertir unidades – Linealizar parámetros
Procesamiento: – Cálculos – Análisis
estadística – Almacenamiento en dispositivos –
Presentación en plantilla o impresora Funciones de un
Computador de Proceso

Supervisión: – Alarmas: verificar el correcto
funcionamiento del proceso – aviso de falla. – Asistencia:
facilitar las operaciones normales del operador. –
Indicación de acciones a ejecutar. Presentación:
entrega información importante para la toma de decisiones
en la operación de mando y control. CUANTIZACIÓN:
En el proceso de conversión A / D o el proceso de
representar una señal en un número finito de
estados discretos, la precisión depende del # de bits de
la palabra de cuantización.

Muestra Cuantización en tiempo Codificación
Cuantización en amplitud Se define un nivel de
cuantización Q que corresponde a la distancia entre dos
niveles adyacentes de decisión. n = # de bits de la
palabra de cuantización. El error de redondeo es: X =
señal análoga. Xq = señal digital


El teorema del muestreo especifica que una señal de tiempo
continua con componentes de frecuencia hasta WC rad/seg,
teóricamente puede ser reconstruida sin distorsión
si se muestrea a una velocidad mayor de 2WC rad/seg. En procesos
con constantes de tiempo mayores se podrá utilizar un
tiempo de muestreo más grande. Debe tenerse en cuenta: El
equipo de medida: se recomienda diseñarlos con una Wcorte
= ancho de banda de red cerrada. El rechazo a las perturbaciones:
Se recomiendan frecuencias de muestreo entre 5 y 20 veces el
ancho de banda de la respuesta al ruido en red abierta. En la
medida en que se exijan tiempo de muestreo más altos, se
requiere de conversores y microprocesadores más
rápidos. Selección del Periodo de Muestreo.

La calidad del control: Generalmente disminuye con periodos de
muestreos largos. Muestrear entre 8 y 10 veces durante el ciclo
de oscilación amortiguada en la señal, si el
sistema es sub-amortiguado. Muestrear de 8 a 10 veces la
frecuencia del ancho de banda de red cerrada, el límite
inferior teórico es 2. Muestrear de 8 a 10 veces durante
el tiempo de subida si es sobreamortiguado.

Tipos de Señales Señal de Tiempo Continuo: (a) (b)
Es una señal que tiene valores para todo instante de
tiempo. Señal Análoga: Es una señal de
tiempo continuo con un rango continuo de valores.

Señal de Tiempo Discreto: Es una señal definida
solamente en instantes del tiempo generalmente iguales.
Señal de datos muestreados Señal Digital Si la
amplitud asume un rango continuo de valores se denomina
señal de datos muestreado. Si los posibles valores
están registrados a un conjunto de valores se denomina
señal digital.

Muestreo y Cuantificación Existen varios tipos de
muestreo: Muestreo Periódico: es el más usual, los
instantes de muestreo están igualmente espaciados cada T
segundos, sea T = KT, T: es el periodo de muestreo, con K
=0,1,2,3,… Muestreo de Orden Múltiple: El
patrón de tK`s se repite periódicamente: tK + r- tK
= constante, para todo tK. Muestreo Múltiple: Sistemas de
múltiples lazos que debido a la dinámica de cada
lazo requieren diferentes periodos de muestreo. Muestreo
Aleatorio: La variable tK es una variable aleatoria.

Tipos de Sistemas De acuerdo al tipo de señal: Sistema
Análogo: Si sólo existen en él
señales análogas se describen mediante ecuaciones
diferenciales. Sistema de Tiempo Discreto: Si sólo existen
en él señales discretas, se describen mediante
Ecuaciones de diferencias. Sistema de Datos Muestreados: Tienen
señales discretas (pulsos de amplitud modulada) y
señales de tiempo continuo Sistema Digital: Si incluye
señales de tiempo continuo y señales digitales en
forma de código numérico.

Sistemas Discretos: Es el que procesa secuencia, es decir recibe
una secuencia y entrega otra, la cual corresponde a una
frecuencia preestablecida de la secuencia de entrada. Secuencia
de salida = f (secuencia de entrada) En bloque funcional: Los
sistemas discretos se clasifican en: Estática
Dinámicos Causales No causales SISTEMA DISCRETO

Sistema Discreto Estática Sistema discreto
estático: La salida en un instante de muestreo depende de
la entrada en ese instante de muestreo Sistema Discreto
Dinámico: La salida puede ser función de la entrada
y la salida de índices de diferente orden al actuar
Sistema Discreto Dinámico

Sistema Discreto Dinámico Causal: El elemento de salida
puede estar influenciada por las salidas anteriores y por las
entradas hasta el instante de muestreo en que se produce la
salida. Sistema no causal: Este sistema puede generar elementos
de índice superior al elemento de entrada, realizar una
función a través de un algoritmo considerando los
elementos generados y entregar una secuencia de salida Sistema
Discreto Dinámico Casual Sistema Discreto Dinámico
no casual

Secuencias: Definición: Un conjunto numerado de elementos
en donde se hace corresponder a cada número entero el
valor de modelos elementos del conjunto de valores de la
señal de tiempo discreto. Una secuencia se representa como
{Xk}, donde K es el entero asociado a cada elemento e indica el
orden de ubicación relativa de ese elemento dentro de la
secuencia, K puede ser positiva o negativa. Se escoge el
índice 0 para indicar el elemento que se encuentra ubicado
en el origen de referencia y que define la frontera entre los
valores positivos y negativos del índice K. Ejemplo:

De igual forma también se puede expresar colocando los
elementos en el orden en que se encuentran en la secuencia. Puede
también especificarse

Secuencia impulso unitario: Secuencia escalón
unitario:

Secuencia exponencial:


Secuencia Sinosoidad

Muestreo de Señales Continuas: El muestreador es un
dispositivo lineal, cumple con el principio de
superposición

Durante el instante del muestreo el muestreador toma la
señal continua y toma la forma de la Fig. (a) para el
desarrollo matemático el muestreador actúa en un ,
el área bajo el impulso es igual al valor o magnitud de la
señal continua en el instante del muestreo, el impulso en
el punto del muestreo es dado por: Donde es el impulso
muestrario. Un muestreador con salida como la ecuación es
como muestreador impulso ideal. La secuencia de impulsos a la
salida del muestreador es:

Nota: Tomando TL a ambos lados de la ecuación

Reconstrucción de señales continuas a partir de
señales discretas Considere la señal de control
producida intermitentemente cada T segundos por un computador
expresado por una serie de impulsos:

Retenedor de orden cero Ideal Retenedor de primer orden

Una simple manera de convertir una señal discreta en una
señal continua es sostener la señal discreta en el
valor constante ___________ hasta que el siguiente valor llegue.
Entonces si es el resultado de la señal continua, para En
particular, para y para para La ecuación anterior
corresponde al retenedor de orden cero

Considerando dos valores discretos sucesivos, y se asume que el
siguiente periodo , la señal continua puede ser dada por
una extrapolación lineal de los dos valores previos para y
La ecuación anterior corresponde al retenedor de primer
orden. El retenedor de primer orden requiere al menos de dos
valores para hacerlo. Construcción de la señal
continua, en tanto que el de orden cero requiere de un solo
valor. Nota: 1. El fundamento matemático del retenedor
independiente del orden es:

Considere una señal continua , el cual debe ser constante
de valores discretos La serie de Taylor alrededor del valor
muestreado es dado por: Si consideramos solo el término de
orden cero, entonces el retenedor de orden cero es: , Si
consideramos el término constante y el de primer
orden:

La derivada de , puede ser aproximada por: Entonces el elemento
retenedor de primer orden: 2. La salida del elemento retenedor de
orden cero es un pulso con una altura constante igual a y una
duración La transformación de Laplace del retenedor
es:

La F. de T. del retenedor de orden cero es: 3. De igual forma la
F. de T. del retenedor de primer orden es:

Conversión de modelos continuos o modelos discretos
Control Digital D/A Convert. retenedor proceso A/D Convert. Ref.
+ –

Caso modelo discreto del retenedor digital PID Sea el valor
muestreado en el instante de muestreo, al compararlo con el valor
del resulta en: , la acción central proporcional es: La
acción de control integral es basado en la
integración del ERROR sobre un periodo de tiempo como los
valores del ERROR son variables en modo discreto, entonces la
Puede ser aproximado por integración numérica
(usando integración rectángular) Área
=

Entonces la acción de control en modo integral está
dado por: Para el modo derivativo necesitamos una
evaluación numérica de la derivada

La aproximación de primer orden para la derivada es:
Entonces la acción de control en el modo derivado es: La
acción de control para el PID digital es modulada: La
ecuación anterior es conocida como ecuación de
diferencias Ejemplo: modelo en tiempo discreto de un proceso de
primer orden.

Dado un proceso no lineal de primer orden: Aproximando la
derivada por diferencia de primer orden ; entonces en un instante
de tiempo dado Para un sistema lineal de primer orden

Usando la aproximación de la derivada, entonces resulta
en: Ejemplo: modelo discreto para un proceso de segundo orden
Dado el sistema lineal La aproximación de la derivada de
primer orden ;

Para la segunda derivada Entonces al reemplazar en la
ecuación del modelo