
¿Por qué unos procesos ocurren en un sentidoy no en
el contrario?

ESPONTANEIDAD. NECESIDAD DE UNA SEGUNDA LEY. 1 Cambio
espontáneo: Aquél que tiende a ocurrir sinnecesidad
de ser impulsado por una influencia externa. ¿Cómo
se puede explicar esta direccionalidad? ¿Con el primer
principio de la Termodinámica? No

No En muchos procesos espontáneos la energía
disminuye. Primeros intentos de explicación La
dirección del cambio químico espontáneo es
aquéllaen la que disminuye la entalpía del sistema.
Reacción exotérmica Û Reacción
espontánea (Gp:) Pero:

SEGUNDO PRINCIPIO DE LATERMODINÁMICA. ENTROPÍA. 2
(Gp:) 1er Principio Energía interna (U) 2º Principio
Entropía (S) (Gp:) Entropía (S) (Gp:)
Función de estado Propiedad extensiva Unidades:
J×K-1

En todo proceso reversible, la entropía del universo
permanece constante. En todo proceso irreversible, la
entropía del universo aumenta. Segundo Principio de la
Termodinámica (Gp:) Proceso reversible: DSuniv = DSsis +
DSent = 0 Proceso irreversible: DSuniv = DSsis + DSent > 0
(Gp:) espontáneo Criterio de espontaneidad: DSuniv >
0

(Gp:) Rudolf Julius Emmanuel Clausius (1822-1888) “Der
Energie der Welt ist konstant;die Entropy der Welt strebt einem
Maximum zu” 1850: Teoría del calor. Energía
como función de estado. 1854: Verwandlungsinhalt. 1865:
Entropía y 2º Pcpio. Termodinámica “La
energía del mundo es constante;la entropía del
mundo lucha por alcanzar un máximo”

Caso particular: Sistema aislado (Gp:) Cualquier proceso deja a
los alrededores sin modificación alguna DSent = 0 Þ
DSuniv = DSsis (Gp:) Proceso reversible, sistema aislado: DSsis =
0 Proceso irreversible, sistema aislado: DSsis > 0 ¡Ojo!
Si no está aislado: Hay que tener en cuentala
variación de entropía del sistema y la de los
alrededores. En un proceso espontáneo aumenta la S del
universo.

La entropía puede considerarse como una medida del
desorden (Gp:) S (Gp:) Sólido (Gp:) Líquido
(Gp:) Gas (Gp:) S (Gp:) S (Gp:) Soluto (Gp:) + (Gp:)
Disolvente (Gp:) Disolución (Gp:) S

¿Cómo es que el agua a menos de 0ºC congela
espontáneamente?¿Acaso no disminuye la
entropía? DSuniv = DSsis + DSent > 0 (Gp:) < 0 (Gp:)
> 0

CÁLCULOS DE ENTROPÍA. 3 3.1. Expansión
isoterma reversible de un gas ideal. (Gp:) T=cte [Levine, pg
58-59,124] DU = 0 (gas ideal y T=cte) [Tema 3]

3.2. Expansión isoterma irreversible de un gas ideal.
(Gp:) S: función de estado 3.3. Cambio de fase. (Gp:)
Vaporización: líq®gas (Gp:) > 0 (Gp:) > 0
> 0 Sgas > Slíq ; DSvap = Sgas- Slíq > 0
Regla de Trouton: A la temperatura de ebullición
estándar,la entropía de vaporización molar
tiene, para muchos líquidos,un valor aproximado de 87
J×K-1×mol-1.

3.4. Cambio de temperatura. (Gp:) P = cte (Gp:) [Tema 3] (Gp:)
SiCp= cte (Gp:) V = cte (Gp:) [Tema 3] (Gp:) SiCv= cte

INTERPRETACIÓN MOLECULARDE LA ENTROPÍA. 4 Un
sistema puede describirse de dos formas: *
Macroscópicamente (P, V, T) * Microscópicamente
(posición y velocidad de cada átomo) Con un estado
macroscópico hay muchos estados
microscópicoscompatibles. La entropía es una medida
del número de estados microscópicosasociados con un
estado macroscópico determinado. Estado
macroscópico: * Ordenado * Desordenado Estado
microscópico: * Orden exacto de los naipes

Un sistema desordenado es más probable que uno
ordenadoporque tiene más estados microscópicos
disponibles. La entropía tiene una tendencia natural a
aumentar dado quecorresponde al cambio de condiciones de baja
probabilidada estados de probabilidad mayor. Implicaciones:
¿cómo se puede explicar la vida? (Gp:) “La
vida es una lucha constante para poder generar
suficienteentropía en nuestro entorno como para seguir
construyendo ymanteniendo nuestras complejas
interioridades” (Gp:) [Atkins, pg 626]

ENTROPÍAS ABSOLUTAS.3er PRINCIPIO DE LA
TERMODINÁMICA. 5 DH = Hprod – Hreac (Gp:) No la usamos
porque no podemosmedir entalpías absolutas. 3er Principio
de la Termodinámica: La entropía de un cristal puro
y perfecto a 0 K es cero. (Gp:) Proporciona un origen de
entropías (Gp:) Podemos tabular entropías
absolutas


Se tabulan entropías molares estándar (Gp:)
Utilidad: Cálculo de entropías de reacción
estándar (DSº) [Mahan, pg 358]
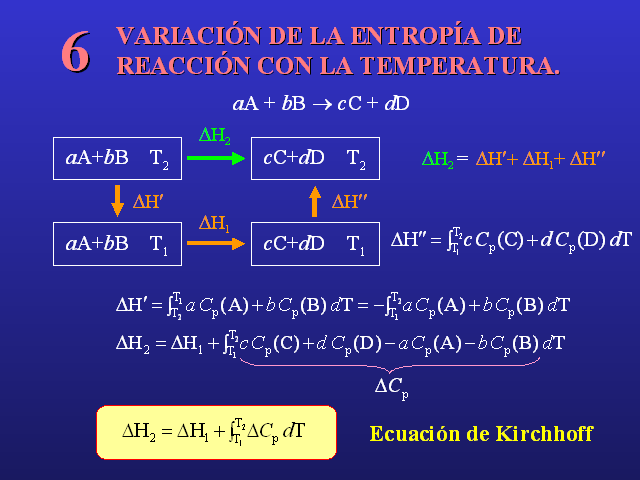
VARIACIÓN DE LA ENTROPÍA DEREACCIÓN CON LA
TEMPERATURA. 6 (Gp:) aA + bB ® cC + dD (Gp:) aA+bB T2 (Gp:)
cC+dD T1 (Gp:) cC+dD T2 (Gp:) aA+bB T1 (Gp:) DH¢ (Gp:)
DH¢¢ (Gp:) DH2 (Gp:) DH1 (Gp:) DH2 = (Gp:) DH¢+
DH1+ DH¢¢ (Gp:) DCp (Gp:) Ecuación de
Kirchhoff

VARIACIÓN DE LA ENTROPÍA DEREACCIÓN CON LA
TEMPERATURA. 6 aA + bB ® cC + dD (Gp:) aA+bB T2 (Gp:) cC+dD
T1 (Gp:) cC+dD T2 (Gp:) aA+bB T1 (Gp:) DS¢ (Gp:)
DS¢¢ (Gp:) DS2 (Gp:) DS1 (Gp:) DS2 = (Gp:) DS¢+
DS1+ DS¢¢ (Gp:) DCp/T

(Gp:) Si DCp=cte

ENERGÍA LIBRE. 7 (Gp:) Criterio de espontaneidad: DSuniv
> 0 (Gp:) ¿No podríamos disponer de un criterio
de espontaneidadexpresado sólo en función de las
propiedades del sistema? (Gp:) Sup. P y T = ctes Qsis = Qp =
DHsis ; Qent = -Qsis = -DHsis

DHsis – TDSsis < 0 Josiah Willard Gibbs (1839-1903)
(Gp:) Energía librede Gibbs (G) G = H – TS (Gp:)
Función de estado Propiedad extensiva Unidades: J DG = DH
– TDS Si DG < 0 proceso irreversible (espontáneo)
Si DG > 0 proceso no espontáneo Si DG = 0 proceso
reversible (equilibrio) A P y T constantes, el sentido del cambio
espontáneo es el sentidode la disminución de
G.

(Gp:) DG = DH – TDS (Gp:) DH DS DG
¿Espontáneo? – + – Sí – si
½DH½>½TDS½ (T bajas) Sí
– – + si ½DH½<½TDS½ (T
altas) No + si ½DH½>½TDS½ (T
bajas) No + + – si
½DH½<½TDS½ (T altas) Sí +
– + No

Energía libre estándar de formación
(DGfº) de una sustancia:Variación de energía
libre estándar de reacción para la formación
de unmol de la sustancia a partir de sus elementos en su estado
más estable.(Unid: J×mol-1) Si DGº < 0
reactivos ® productos: espontánea Si DGº > 0
reactivos ® productos: no espontánea (reactivos ¬
productos: espontánea) Si DGº = 0 estado de
equilibrio: reactivos « productos (Gp:) DHfº Sº
(Gp:) DHº DSº (Gp:) DGº = DHº –
TDSº