
2 Supongamos, como es habitual, que estamos utilizando una
calculadora electrónica para realizar operaciones
aritméticas. Es también bastante común que
operemos entre valores que tienen diferentes números de
cifras, por ejemplo: 755,250 / 133,04 La calculadora normalmente
expresa el resultado empleando todo su visor, es decir que el
número final se presenta con 8, 10 ó 12
dígitos, según la máquina. En nuestro caso
el resultado es: Cifras significativas y redondeo
5,676864101

3 La tendencia generalizada para expresar el resultado es tomar
todos los decimales mostrados o bien efectuar un
“redondeo” con cierta arbitrariedad. En nuestro
planteo podría ser: 755,250 / 133,044 = 5,676864101 o bien
7,55 / 1334 = 5,67 Veremos que ninguno de los dos métodos
tiene un sentido claro, en especial cuando el valor final se
obtiene con números medidos o calculados a partir de
magnitudes obtenidas por determinaciones con instrumentos de
medición. Se dará un concepto importante en los
cálculos numéricos: es el de las “cifras
significativas” de un número, (dígitos
significativos ó cif.sig.), que debe ser siempre tenido en
cuenta. Cifras significativas y redondeo

4 En efecto, sea un valor numérico cualquiera, resultado
de una medición o de un cálculo aritmético.
Estará compuesto en general por “n”
dígitos y tendrá una parte entera y una decimal,
separadas por la “coma” correspondiente. Tanto una
parte como la otra pueden ser nulas y también puede valer
“0” cualquier dígito intermedio. Del total de
“n” valores, existe sin ninguna duda, un grupo menor
de dígitos que se conocen o se deben conocer con
seguridad. Se puede hablar en consecuencia de: Cifras
Significativas El concepto señalado se asocia, ya sea con
el tema de que se trate (geométrico, contable,
físico, etc.) o bien con la “exactitud” de los
datos del cálculo. La determinación de las cifras
significativas de un número, para diferentes casos, se
detalla en las siguientes reglas: Cifras significativas y
redondeo

5 1. Los dígitos distintos de cero siempre son
significativos, cualquiera sea su posición (sean de la
parte entera o de la parte decimal): a) 137,4 4 cif.sig. b) c) d)
3415,9 852, 283 45 5 6 2 “ “ “ 2. Los ceros a
la izquierda del primer dígito distinto de cero nunca son
significativos (tanto en la parte entera como en la decimal): e)
0,375 3 cif.sig. f) g) h) 0,000375 0,002978 0,00085 3 4 2 “
“ “ Cifras significativas y redondeo
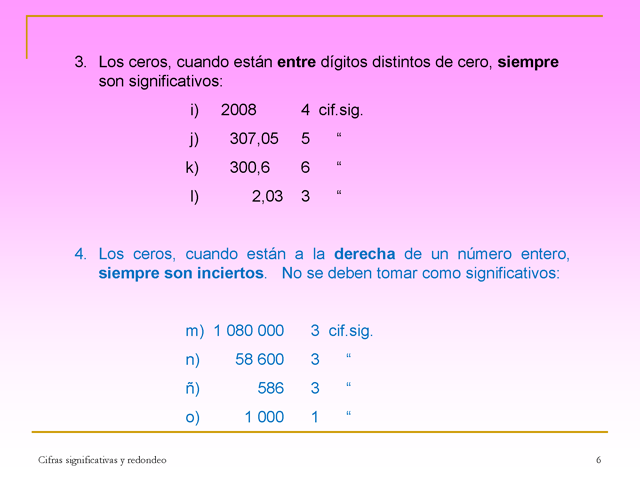
i) 6 3. Los ceros, cuando están entre dígitos
distintos de cero, siempre son significativos: 2008 4 cif.sig. j)
k) l) 307,05 300,6 2,03 5 6 3 “ “ “ 4. Los
ceros, cuando están a la derecha de un número
entero, siempre son inciertos. No se deben tomar como
significativos: m) 1 080 000 3 cif.sig. n) ñ) o) 58 600
586 1 000 3 3 1 “ “ “ Cifras significativas y
redondeo

coma t) 7 5. Los ceros, al final de un número, si
están después de la decimal, siempre son
significativos: p) 42,0 3 cif.sig. q) r) s) 42,000 206,0 1,020 5
4 4 “ “ “ 6. En el caso de que un número
cualquiera, esté expresado en notación
científica de la forma: N = a . 10n , el número de
cif.sig. siempre es el de las cifras significativas de
“a”, pero deben incluirse en este caso, todos los
ceros de “a”, en cualquier posición en que se
encuentren: 7,31 . 104 3 cif.sig. u) v) w) 2,10 . 106 2,100. 106
5,029 402 . 108 3 4 7 “ “ “ Cifras
significativas y redondeo

10 • Si se efectuara un riguroso “cálculo de
errores”, las afirmaciones que siguen podrían
expresarse con mas propiedad. Pero lo que se quiere destacar es
un comportamiento sencillo frente a la interpretación de
los resultados antes señalados. Se puede enunciar la
siguiente regla: “Cuando se realiza un cálculo
aritmético y se opera con valores numéricos que
tienen, cada uno de ellos, un número propio de cifras
significativas, el resultado tendrá como máximo un
valor de éstas, correspondiente al mas corto de los
operandos. • De otra manera, si admitimos que la
“exactitud” de un valor es mayor, cuanto mayor es el
número de cif.sig., se puede afirmar: “el resultado
no puede ser mas exacto, que el valor menos exacto involucrado en
el cálculo”. Cifras significativas y redondeo

x) / / z) a) 11 Algunos Ejemplos de cálculos: 7,55 / 1334
= 0,00565967 (forma incorrecta) 7,55 / 1334 = 0,0056 (forma
incorrecta) 7,55 / 1334 = 0,00565 (forma correcta; 3 cif.sig.) y)
89,3 89,3 0,210 = 425,238 095 2 (incorrecto) 0,210 = 425
(correcto; 3 cif.sig) (9,29 . 102) x (2,62 . 103) = 2 433 980
(incorrecto) (9,29 . 102) x (2,62 . 103) = 2,43 . 106 (correcto;
3 cif.sig.) 0,12 x 1000 = 120 ( correcto; 2 cif.sig.) Cifras
significativas y redondeo

• 12 Un tema íntimamente relacionado con lo anterior
es el tratamiento de las cifras decimales de un número,
con el objeto de reducir su longitud. Se suele hacer de dos
maneras: 1. Truncado: simplemente se “eliminan” todos
los dígitos significativos después de
“k” de ellos: por ej. sea 2/3 = 0,666666666 si k = 4
pero si k = 2 2/3 = 0,6666 2/3 = 0,66 2. Redondeo: para un dado
valor de “k”, si el decimal “k+1” es 0;
1; 2; 3 ó 4, se trunca en k; pero si “k+1”
vale 5; 6; 7; 8; ó 9, el decimal “k” se
incremente en 1 y se trunca en k. por ej. Sea 2/3 = 0,666666666
Cifras significativas y redondeo si k = 4 ó si k = 2 2/3 =
0,6667 2/3 = 0,67

13 • El método que conduce a mejores resultados y
también el mas utilizado es el de redondeo. • Tomemos
por ejemplo redondear el número p = 3,141592654 tal como
lo expresa el visor de una calculadora, con 9 cifras decimales:
redondeo a 8 cifras decimales: 3,14159265 “ “ 7
“ 6 “ : : 3,1415927 3.141593 “ “ “
“ “ 5 4 3 2 1 “ “ “ “ “
“ “ “ “ “ : : : : : 3,14159 3,1416
3,142 3,14 3,1 Cifras significativas y redondeo

14 • Si se tuviese que calcular la longitud de una
circunferencia, teniendo como dato el diámetro, con un
valor de 12,54 m (4 cif.sig.), de acuerdo con lo visto
anteriormente, solo tendría sentido utilizar un valor de p
= 3,142 (también de 4 cif.sig): Long.circunf. = p .
Diám. = 3,142 x 12,54 m = 39,40068 m Valor que redondeado
al 2º decimal es : 39,40 m (4 cif.sig.) • Por otra
parte, si hubiésemos utilizado para el cálculo un
valor de p con todos los decimales tendríamos:
Long.circunf. = 3,141592654 x 12,54 m = 39,39557188 m Valor que
redondeado al 2º decimal es nuevamente : 39,40 m • Se
comprueba claramente que no se obtiene un valor
“mejor” por utilizar un gran número de
decimales. Se suele creer falsamente, que se mejora la
“exactitud” de un cálculo empleando muchas
cifras. Cifras significativas y redondeo

15 • Veamos otro ejemplo: 4,21 x 0,78508 = 3,3051868 4,21 x
0,78535 = 3,3063235 4,21 x 0,78554 = 3,3071234 4,21 x 0,78573 =
3.3079233 4,21 x 0,78592 = 3,3087232 • En todos estos
productos el factor con menos cifras significativas es 4,21 (3
cif.sig.), en consecuencia el resultado solo puede tener como
máximo también 3 cif.sig. • Con el criterio de
redondeo visto, el valor final sería: 3,31 Este valor es
sensiblemente independiente de las cifras decimales de orden
superior del segundo factor. Cifras significativas y redondeo