Álgebra de Boole. Fundamentos y aplicaciones básicas en la electrónica digital moderna (Presentación PowerPoint)

2 • La profundización teórica del tema
“Algebra de Boole” puede ser consultada en una
extensa bibliografía, a la que no se pretende reemplazar.
Simplemente entrando en “Internet”, en un
“buscador” como “Google”, “Algebra
de Boole” permite acceder a muchos artículos de gran
calidad. • Solo daremos una definición y
mencionaremos los enunciados de algunas leyes básicas (sin
discriminar entre “postulados” y
“teoremas”), como para iniciarnos en este tema.
• La idea fundamental es empezar a entender el
Álgebra de Boole en el contexto de las aplicaciones en la
electrónica digital moderna. • Con los ejemplos que
se verán, se pretende tener una idea razonablemente clara
sobre los principios elementales de funcionamiento que rigen los
sistemas de cálculo de máquinas ariméticas y
computadoras electrónicas. Algebra de Boole –
Aplicaciones

• o * • • 3 Definición del Álgebra
de Boole Es toda clase o conjunto de elementos que: 1. pueden
tomar dos valores estados claramente distintos (o perfectamente
diferenciados ) 2. están relacionados entre sí por
dos operaciones binarias*, llamadas suma lógica (+) y
producto lógico (·). operación binaria es
aquella que, definida entre elementos de un conjunto, da por
resultado un elemento del mismo conjunto. Se incorpora
también la negación ( ´ ), aunque no entre en
la definición. Son ejemplos de álgebras de Boole:
el álgebra de proposiciones o de juicios formales y el
álgebra de redes eléctricas o de
conmutación, vistos anteriormente. Algebra de Boole –
Aplicaciones

4 • Las variables o elementos, se indican con letras
mayúsculas: A, B, C, D, etc. .(aunque en
“Álgebra Proposicional”, como se acostumbra,
se hayan utilizado letras minúsculas). También se
pueden utilizar números o nombres representativos. •
Los dos estados posibles se anotan: “0” y
“1”. • De igual manera que en el álgebra
convencional, la suma lógica se indica con (+) y el
producto lógico con (·) o simplemente se elimina.
• Así el producto a·b se puede poner ab . La
negación puede señalarse con: – , ~, con un
guión superior o simplemente con ´. Por ejemplo la
función lógica: puede escribirse: F =
A+B+(B·(-C)) · ( (~D)+E) F = A+B+(BC)(D+E) Algebra
de Boole – Aplicaciones
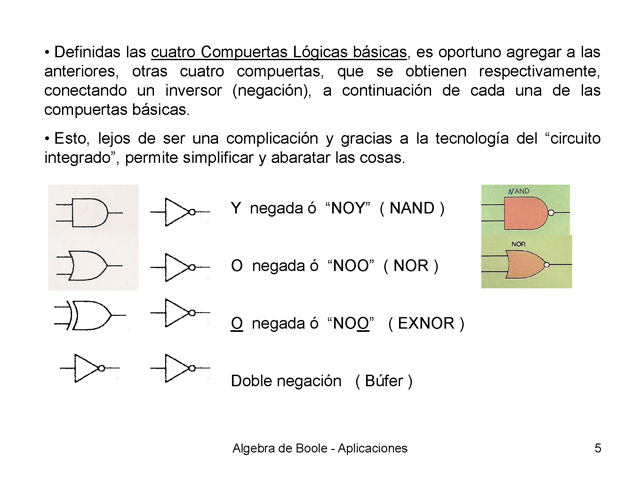
5 • Definidas las cuatro Compuertas Lógicas
básicas, es oportuno agregar a las anteriores, otras
cuatro compuertas, que se obtienen respectivamente, conectando un
inversor (negación), a continuación de cada una de
las compuertas básicas. • Esto, lejos de ser una
complicación y gracias a la tecnología del
“circuito integrado”, permite simplificar y abaratar
las cosas. Y negada ó “NOY” ( NAND ) O negada
ó “NOO” ( NOR ) O negada ó
“NOO” ( EXNOR ) Doble negación ( Búfer
) Algebra de Boole – Aplicaciones

6 • En la tabla se indican los símbolos
gráficos de las nuevas compuertas, que se forman
agregándole en la salida de las básicas, un
pequeño circulo que indica la inversión. •
También en cada caso está la “tabla de
verdad” y la correspondiente “Expresión
Booleana”. Algebra de Boole – Aplicaciones

7 • Existen compuertas de hasta ocho entradas. Ejemplos de
símbolos y Tablas de Verdad, se dan a continuación,
para tres y cuatro entradas, tanto para NAND como para NOR.
Algebra de Boole – Aplicaciones

8 • Habiendo definido : las “proposiciones” los
“conectivos lógicos” las “compuertas
lógicas” y sus correspondientes
“símbolos gráficos”, podemos a partir
de ahora operar con estos conceptos a través del:
“Algebra de Boole”. • En nuestros razonamientos
nos independizaremos de los elementos materiales, aunque a
título informativo mencionaremos, cuando corresponda, los
componentes reales existentes. Algebra de Boole –
Aplicaciones

9 Enunciados, teoremas, propiedades, leyes ó reglas del
Algebra de Boole. En cada caso, se da a continuación del
nombre de la propiedad, la expresión matemática
Booleana, la materialización en forma de circuito de
compuertas simples y una breve explicación. Para mayor
claridad, se presenta la misma tabla en dos secciones. Algebra de
Boole – Aplicaciones
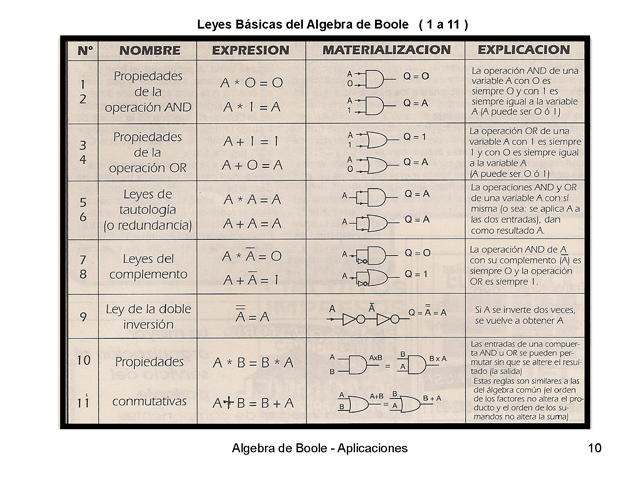
10 Leyes Básicas del Algebra de Boole ( 1 a 11 ) Algebra
de Boole – Aplicaciones

11 ( 12 a 22 ) Algebra de Boole – Aplicaciones

• 12 • Una primera aplicación de los conceptos
anteriores es proponerse sintetizar una “Disyunción
Excluyente O (EXOR)”, utilizando solo compuertas
básicas O, Y y NO (OR, AND y NOT). A 0 B 0 Y 0 Recordemos
el símbolo y su tabla de verdad: 0 1 1 1 0 1 1 1 0 La
tabla se puede describir con palabras, de varias formas, por
ejemplo: 1. La salida toma el estado “1”, si una y
solo una de las entradas está en “1”. 2. La
salida es “1”, si A = 1 ó B = 1, pero no ambas
a la vez. Esta expresión nos llevaría a : A O B =
(A+B) . (AB) 3. La salida es “0”, si A y B son ambas
iguales a “1” ó ambas iguales a
“0”. La función Booleana sería: A O B =
(A B) + (A B) 4. La salida es “0”, si ambas entradas
son iguales entre sí. Algebra de Boole – Aplicaciones Etc.
Etc. Etc.

) 13 • De esta manera en forma intuitiva, se puede encontrar
la expresión Booleana conveniente. Pero cuando el problema
se complica porque el enunciado que se plantea es mas avanzado,
se requiere entonces tener alguna forma sistemática para
expresar la función lógica correspondiente. •
El método que se propone, entre otros, se llama
“Suma de Productos” y consiste en: 1º Crear la
tabla de verdad del enunciado planteado. A 0 0 1 1 B 0 1 0 1 Y 0
1 1 0 2º Disponer de una suma de tantos paréntesis
como “unos” haya en la tabla de verdad, en la
proposición de salida. En nuestro caso: dos. AOB = ( ) + (
3º Dentro de cada paréntesis irá un producto
lógico entre todas las variables de la entrada,
tomándolas directas cuando valgan “1” y
negadas cuando su valor sea “0”: A O B = ( A. B ) + (
A . B ) Algebra de Boole – Aplicaciones

14 • Cada producto formado se llama
“minitérmino” y resulta claro que su valor
será “1”, solo cuando se dé la
combinación de “0s y 1s” correspondiente. A O
B = ( AB ) + ( A B) • Finalmente el circuito de compuertas
lógicas para el O excluyente, será: Algebra de
Boole – Aplicaciones

15 • Para continuar con aplicaciones significativas, se
propone tomar como objeto, el funcionamiento macroscópico
de una simple calculadora digital de cuatro operaciones. •
Recordemos que en la vida diaria se utiliza la familiar
numeración decimal, pero toda máquina que realice
operaciones aritméticas, desde una simple calculadora
hasta la mas compleja computadora, opera internamente, sin
ninguna excepción, en el sistema de numeración
binaria. • Se crea entonces la necesidad de introducir un
“sistema codificador” en la entrada de la
máquina, que vincule el teclado numérico exterior
con los elementos internos de cálculo. • Enunciado:
Codificador Decimal a Binario: Se trata de convertir al sistema
binario natural, un dígito expresado en forma decimal.
Tendrá evidentemente diez entradas vinculadas a las
teclas, de forma tal que cuando solo una de ellas es oprimida,
aparezca en cuatro puntos internos, el conjunto de ceros y unos
de la combinación binaria natural correspondiente. Algebra
de Boole – Aplicaciones

16 • Planteo Lógico: Llamaremos con los
dígitos 0; 1; 2; 3; 4; 5; 6; 7; 8 y 9, a las diez
proposiciones de entrada (cada tecla tiene dos estados: oprimida
o no). • Las proposiciones de salida serán D; C; B y
A y estarán en correspondencia con los valores de cada
posición binaria 8; 4; 2 y 1. las entradas, se toma como
“tecla oprimida”. El valor lógico
“1” para 0 1 0 0 1 0 1 0 2 0 0 1 3 0 0 0 4 0 0 0 5 0
0 0 6 0 0 0 7 0 0 0 8 0 0 0 9 0 0 0 D 0 0 0 C 0 0 0 B 0 0 1 A 0 1
0 • Tabla de Verdad: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 1 1 1 1 0 0 1 0
0 1 1 0 0 1 0 1 0 1 0 1 Algebra de Boole – Aplicaciones

17 • Con la observación de la tabla se deducen, en
forma intuitiva, las correspondientes “Funciones
Booleanas”: A = 1+3+5+7+9 B = 2+3+6+7 Entradas desde el C =
4+5+6+7 D = 8+9 Que se materializan con el circuito de compuertas
lógicas “ O “, de varias entradas. A B C D
teclado. Algebra de Boole – Aplicaciones

18 • La siguiente aplicación nos lleva a la
operación inversa de la anterior, es decir el
órgano de cálculo arroja un resultado
numérico binario, y debe interpretarse como un
número decimal. • La necesidad ahora es de crear un
sistema “decodificador” en el interior de la
máquina. • Enunciado: Decodificador Binario a Decimal
. Se trata de convertir un binario natural en un dígito
decimal. El sistema tendrá cuatro proposiciones de
entrada, diez de salida y estarán vinculadas de manera tal
que para cada combinación de los estados binarios, se
excite solo la salida decimal correspondiente. • Planteo
Lógico: En forma semejante al caso anterior, esta vez las
proposiciones de entrada serán las letras D; C; B; y A ,
mientras que con los dígitos 0; 1; 2; . . .9 se nombran
las diez proposiciones de salida. Algebra de Boole –
Aplicaciones

19 D C B A 0 1 2 3 4 5 6 7 8 9 • Tabla de Verdad: 0 0 0 0 0
0 0 1 1 1 Los espacios en blanco son obviamente
“ceros”, que no se 0 0 0 0 1 1 0 1 1 1 colocan para
mayor claridad de la tabla. 0 0 0 0 1 1 1 1 1 1 0 0 0 0 1 1 0 0 0
1 0 1 0 1 1 1 1 1 1 1 Funciones Booleanas: Aplicando el
método de Suma de productos se tendrá para cada
proposición de salida, un único producto
lógico entre las variables de entrada. Se toman directas
si valen “1” y serán negadas si valen
“0”. Algebra de Boole – Aplicaciones

0 2 3 4 5 6 7 8 9 20 Circuito de Compuertas Lógicas: 1 Los
inversores colocados en cada entrada, proveen al sistema la
posibilidad de elegir la proposición directa o negada
según la tabla. Es muy utilizado el recurso de generar
barras con las proposiciones directas y negadas. No solo se
ahorran inversores, sino que se hace mas sencilla la
interpretación del gráfico y se simplifica el
cableado. Se utilizan solo compuertas Y (AND). Algebra de Boole –
Aplicaciones

8 21 A 0 • En este segundo circuito hay algunas
simplificaciones. B 1 2 • Como vemos solo hay dos 3
compuertas NAND de cuatro entradas, seis de tres entradas y dos
de dos entradas, en vez de utilizar diez compuertas de cuatro
entradas. C D 4 5 6 7 • Las compuertas NAND proveen
simplificaciones en los sistemas posteriores. Algebra de Boole –
Aplicaciones 9

A B C 22 • Siguiendo con la calculadora elemental,
observemos que la indicación numérica del visor, se
realiza mediante una representación llamada de “
Siete segmentos “ ó de “Siete Barras”.
Todos estamos familiarizados con esta indicación, que
también se utiliza en ascensores, indicadores
numéricos, relojes digitales, etc. • Los segmentos
luminosos pueden ser “cristales líquidos (LCD) en
calculadoras y relojes, ó diodos LED, lámparas
comunes o hasta tubos fluorescentes en otros sistemas . Pero la
denominacion de los segmentos generalmente aceptada es la que se
indica. • Decodificador ABCD a 7 segmentos. • El
enunciado y el planteo lógico de este circuito, resulta
claro con el gráfico que se agrega. D Algebra de Boole –
Aplicaciones

23 • Tabla de Verdad del decodificador BCD a 7 Seg. Nº
0 1 2 3 4 5 6 7 8 9 D 0 0 0 0 0 0 0 0 1 1 C 0 0 0 0 1 1 1 1 0 0 B
0 0 1 1 0 0 1 1 0 0 A 0 1 0 1 0 1 0 1 0 1 a 1 0 1 1 0 1 1 1 1 1 b
1 1 1 1 1 0 0 1 1 1 c 1 1 0 1 1 1 1 1 1 1 d 1 0 1 1 0 1 1 0 1 1 e
1 0 1 0 0 0 1 0 1 0 f 1 0 0 0 1 1 1 0 1 1 g 0 0 1 1 1 1 1 0 1 1
• Para expresar las funciones Booleanas se puede aplicar el
método de la Suma de Productos. Por ejemplo para reconocer
el segmento “a”se tendría una suma
lógica de ocho productos; para el segmento “e”
solo cuatro productos; etc. • Inmediatamente se comprueba
que las expresiones son muy largas. Algebra de Boole –
Aplicaciones

24 Algebra de Boole – Aplicaciones

1 2 3 4 7 9 25 • Cabe hacer varias simplificaciones
Booleanas y algunas experimentales, pero por sencillez no daremos
el detalle. A B C D 0 • El circuito de Compuertas
Lógicas ya simplificado, pero razonablemente entendible se
muestra a continuación: 5 6 • Se puede reconocer a la
izquierda del dibujo, una versión del decodificador
binario a decimal anterior. a b c d e f g Algebra de Boole –
Aplicaciones

26 • De los Circuitos Lógicos anteriores vimos que,
aún cuando se han simplificado bastante, la
implementación práctica de los mismos
requirió el empleo de muchas compuertas elementales.
• Si se tiene en cuenta que la solución encontrada
fue para un solo dígito decimal y normalmente su manejan
como mínimo ocho dígitos, empezamos a vislumbrar el
crecimiento de la cantidad de “compuertas
lógicas” que son necesarias disponer en cuanto se
avanza en el diseño de un dispositivo tan
“simple” como una sencilla calculadora. • Nos
ocuparemos ahora, en forma muy somera, de lo relativo a los
elementos de cálculo, que naturalmente también
serán resueltos con compuertas lógicas elementales.
• Mostraremos primero, como funciona un circuito
“Sumador Digital”. Algebra de Boole –
Aplicaciones

27 • Se considera necesario hacer un esquema en bloques que
permita fijar conceptualmente lo que todos sabemos: como se
realiza una “Suma”. Por supuesto que se describe en
términos de una adición entre dos números
binarios de cuatro dígitos cada uno. D1 D2 C1 C2 B1 B2 A1
A2 Sumador AcD SD AcC SC AcB SB AcA SA • Distinguimos entre
el primer bloque de la derecha, que recibe dos entradas y genera
dos salidas y que se lo llama “Semisumador” y los
siguientes bloques que reciben tres entradas y tienen
también dos salidas y son nombrados como “Sumador
Total”. Algebra de Boole – Aplicaciones

30 • Tabla de verdad del Semisumador: Llamaremos A1 y A2 a
los dígitos de entrada; SA a la suma directa y AcA al
acarreo, arrastre o el simple “me llevo”. • En
la tabla, podemos ver que la suma equivale a un “o
excluyente” (O), mientras que el acarreo es claramente
equivalente a la “conjunción” (Y). •
Estas observaciones nos llevan directamente a las funciones
Booleanas: A1 0 0 1 1 A2 0 1 0 1 AcA 0 0 0 1 SA 0 1 1 0 SA = A1 O
A2 = (A 1 . A2) + (A1 . A2) AcA = A1 . A2 • El circuito de
compuertas lógicas muestra una compuerta Y y un O
excluyente (O) que por supuesto puede ser reemplazado por el
diagrama ya visto. Algebra de Boole – Aplicaciones A1 A2 SumaA
AcA

31 • Tabla de verdad del Sumador Total: En este caso las
entradas son tres, no solo los dos dígitos a sumar B! Y B2
, sino también el arrastre anterior AcA. Las salidas son
solo dos, una la suma SB y la segunda el acarreo AcB. AcA B2 B1
AcB SB Acarreo Suma 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0
1 0 0 0 1 0 1 1 1 0 1 1 0 1 0 0 1 Algebra de Boole –
Aplicaciones

34 • Ecuaciones Booleanas: Aplicamos a la tabla precedente
el método de la “suma de productos”. Tenemos
en cada caso cuatro unos, que originan la suma lógica de
cuatro productos, respectivamente para cada salida. SB = (AcA B1
B2) + (AcA B1 B2) + (AcA B1 B2) + (AcA B1 B2) 1 2 3 4 AcB = (AcA
B1 B2) + (AcA B1 B2) + (AcA B1 B2) + (AcA B1 B2) 5 6 7 8 Se
pueden simplificar sacando factor común AcA de 1 y 2 y
luego AcA de 3 y 4. Se obtiene que: SB = AcA (B1 O B2) + AcA (B1
O B2) Y además de 5 y 8 y de 6 y 7 : AcB = B1 B2 + AcA (
B1 O B2) Algebra de Boole – Aplicaciones

35 • Circuito de compuertas lógicas debidamente
simplificado. Responde a las expresiones recuadradas anteriores.
El O entre las entradas B1 y B2, aparece en ambas ecuaciones,
pero no se repite en el esquema. AcA B2 B1 Algebra de Boole –
Aplicaciones Acarreo o arrastre AcB Suma SB

36 • Se demuestra que la “Resta” puede ser
efectuada, en numeración binaria, mediante una suma, por
supuesto que utilizando un cierto artificio de electrónica
digital que no merece llamarse operación, pero donde
también se usan compuertas lógicas. (Se demuestra
en el apéndice). • La Multiplicación, sabemos
que por definición es una suma reiterada. • La
División también puede verse como la
repetición de una resta, que a su vez se puede convertir
en sumas. • Por lo tanto, aún sin
demostración, se puede afirmar que con
“sumadores” y algunos “artilugios”
adecuados, concebimos con relativa facilidad la idea de que, las
operaciones aritméticas elementales, se realizan en los
sistemas de cálculo actuales, respaldados por las ideas
que aquí se han desarrollado. Algebra de Boole –
Aplicaciones

1º 37 • Para finalizar, es útil mostrar como se
puede concebir un elemento de “memoria” de un
“bit”, empleando solamente dos inversores. Se trata
de “retener” un “0” ó un
“1”, cuando éste se aplique durante un corto
período de tiempo. • Un “0” de corta
duración en la entrada A, impone un “1” en B a
través del 1º inversor; a A B la vez que el 2º
inversor coloca un “0” permanente en A, aunque el
valor original en la entrada haya desaparecido. B 2º A
• En igual forma un “1” de corta duración
en A, es retenido o memorizado con una consideración
complementaria de la anterior. • Existen muchas variantes de
memoria, basadas en otras compuertas lógicas, pero esta es
significativa por su simpleza. Algebra de Boole –
Aplicaciones

38 • Se puede continuar con la síntesis de muchos
circuitos que cumplan diferentes tareas en los sistemas de
computación, pero creemos que el objetivo de fundamentar
las bases “Lógico-matemáticas” de esta
moderna técnica, ha sido cumplido. • Gracias por su
atención. • Se sugiere comentar el tema. FIN Algebra
de Boole – Aplicaciones

• 39 APÉNDICES: 1. “Decodificador o Selector de
16 Direcciones”. 2. Código ASCII . 3. Familia TTL de
compuertas lógicas integradas. 4. Multiplexor y
Demultiplexor 5. Varios. Algebra de Boole – Aplicaciones

40 Decodificador “ Binario a Decimal o a Hexadecimal(16
salidas)” (4 : 16), tambien llamado “Selector de
Direcciones”. Algebra de Boole – Aplicaciones

ESTA PRESENTACIÓN CONTIENE MAS DIAPOSITIVAS DISPONIBLES EN
LA VERSIÓN DE DESCARGA