
(Gp:) LONGITUD DE ONDA (l) (Gp:) 10 -13 10 -11 10 -9 10 -7 10 -5
10 -3 10 -2 10 -1 10 0 10 2 10 3 metros (m) (Gp:) FRECUENCIA (n)
(Gp:) 10 21 10 19 10 17 10 15 10 13 10 11 10 10 10 9 10 8 10 6 10
5 Hertz (Hz) (Gp:) RAYOS GAMMA RAYOS X UV VISIBLE INFRARROJO
MICROONDAS ONDAS DE RADIO (Gp:) RMN (Gp:) Grupos funcionales
(Gp:) Núcleos individuales (Gp:) IR (Gp:) UV
Introducción El fenómeno de la RMN fue descubierto
por Purcell y Bloch (Premio Nobel de Física 1952) 1
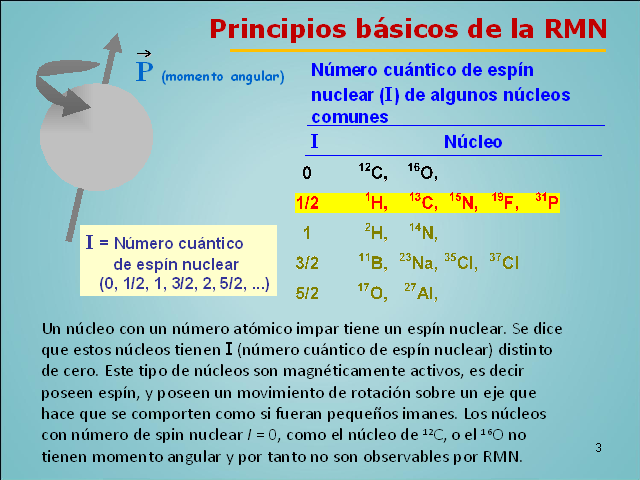
2 I = Número cuántico de espín nuclear (0,
1/2, 1, 3/2, 2, 5/2, …) (Gp:) P (momento angular) Principios
básicos de la RMN (Gp:) Número cuántico de
espín nuclear (I) de algunos núcleos comunes I
Núcleo Un núcleo con un número
atómico impar tiene un espín nuclear. Se dice que
estos núcleos tienen I (número cuántico de
espín nuclear) distinto de cero. Este tipo de
núcleos son magnéticamente activos, es decir poseen
espín, y poseen un movimiento de rotación sobre un
eje que hace que se comporten como si fueran pequeños
imanes. Los núcleos con número de spin nuclear I =
0, como el núcleo de 12C, o el 16O no tienen momento
angular y por tanto no son observables por RMN. ?
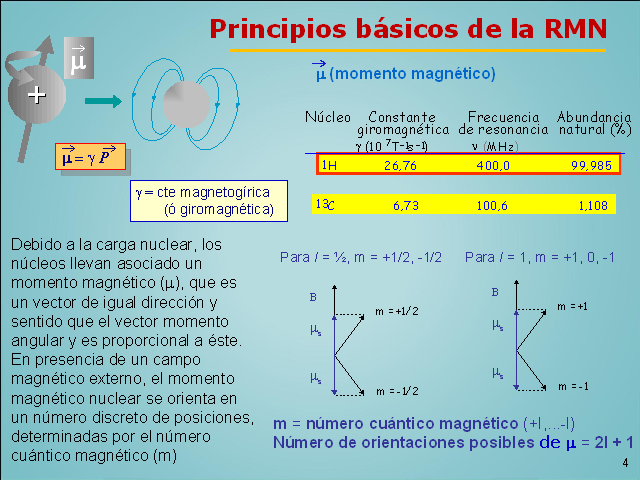
3 Principios básicos de la RMN Para I = ½, m =
+1/2, -1/2 Para I = 1, m = +1, 0, -1 (Gp:) ?z (Gp:) ?z (Gp:) B
(Gp:) m = +1/2 (Gp:) m = -1/2 (Gp:) ?z (Gp:) ?z (Gp:) B (Gp:) m =
+1 (Gp:) m = -1 m (momento magnético) m = número
cuántico magnético (+I,…-I) Número de
orientaciones posibles de m = 2I + 1 (Gp:) m (Gp:) + (Gp:) m = g
P (Gp:) g = cte magnetogírica (ó
giromagnética) (Gp:) Núcleo (Gp:) Constante (Gp:)
Frecuencia (Gp:) Abundancia (Gp:) giromagnética (Gp:) de
resonancia (Gp:) natural (%) (Gp:) g (Gp:) (10 (Gp:) 7 (Gp:) T
(Gp:) -1 (Gp:) s (Gp:) -1 (Gp:) ) (Gp:) n (Gp:) (MHz) (Gp:) 1
(Gp:) H (Gp:) 26,76 (Gp:) 400,0 (Gp:) 99,985 (Gp:) 13 (Gp:) C
(Gp:) 6,73 (Gp:) 100,6 (Gp:) 1,108 ? ? ? ? Debido a la carga
nuclear, los núcleos llevan asociado un momento
magnético (m), que es un vector de igual dirección
y sentido que el vector momento angular y es proporcional a
éste. En presencia de un campo magnético externo,
el momento magnético nuclear se orienta en un
número discreto de posiciones, determinadas por el
número cuántico magnético (m)

4 (Gp:) Polo magnético (Gp:) Polo magnético (Gp:)
B0 (Gp:) a (m=+1/2) (Gp:) b (m=-1/2) (Gp:) DE = hn (Gp:) a (Gp:)
a (Gp:) a (Gp:) b (Gp:) b (Gp:) b E INFLUENCIA DE UN CAMPO
MAGNÉTICO EXTERNO Núcleos con I = 1/2

5 Campo Magnético (B0) Energía a b INFLUENCIA DE UN
CAMPO MAGNÉTICO EXTERNO (Gp:) g hBo (Gp:) 2p (Gp:) ?E = hn
= n = Frecuencia de Larmor (Gp:) g Bo (Gp:) 2p (Gp:) n = (Gp:)
Frecuencia de Larmor La frecuencia requerida para pasar del
estado ? al ? (que en realidad es simplemente un cambio en la
orientación del spin nuclear), se denomina frecuencia de
resonancia (n) y es proporcional a Bo y a g.

6 (Gp:) (Gp:) Núcleo (Gp:) Constante (Gp:) Frecuencia
(Gp:) Abundancia (Gp:) giromagnética (Gp:) de resonancia
(Gp:) natural (%) (Gp:) g (Gp:) (10 (Gp:) 7 (Gp:) T (Gp:) -1
(Gp:) s (Gp:) -1 (Gp:) ) (Gp:) n (Gp:) (MHz) Para un campo
magnetico Bo = 9.4 T (Gp:) 1 (Gp:) H (Gp:) 26,76 (Gp:) 400,0
(Gp:) 99,985 (Gp:) 2 (Gp:) H (Gp:) 4,11 (Gp:) 61,4 (Gp:) 0,015
(Gp:) 13 (Gp:) C (Gp:) 6,73 (Gp:) 100,6 (Gp:) 1,108 (Gp:) 14
(Gp:) N (Gp:) 1,93 (Gp:) 28,9 (Gp:) 99,63 (Gp:) 15 (Gp:) N (Gp:)
-2,71 (Gp:) 40,5 (Gp:) 0,37 (Gp:) 17 (Gp:) O (Gp:) -3,63 (Gp:)
54,3 (Gp:) 0,037 (Gp:) 19 (Gp:) F (Gp:) 25,18 (Gp:) 376,5 (Gp:) 1
(Gp:) 00,0 (Gp:) 31 (Gp:) P (Gp:) 10,84 (Gp:) 162,1 (Gp:) 100,0
Principios básicos de la RMN Cada núcleo tiene su
frecuencia de resonancia característica, que depende de su
constante giromagnética y del campo magnético
externo aplicado.

7 2.2. Niveles poblacionales, 1 Na Nb = e (Gp:) Ej.: Para Bo =
4,7 Teslas y T = 300 K (Gp:) kT (Gp:) DE (Gp:) = 6,4 x 10-5 (Gp:)
Nb (Gp:) Na (Gp:) = 1.00006 (Gp:) DE << kT (Gp:) Na ? Nb
(Gp:) En RMN (Gp:) DE >> kT (Gp:) Na >> Nb (Gp:) En
otras espectroscopias (Gp:) En RMN es como si detectáramos
sólo 1 de cada 100.000 núcleos presentes (Gp:)
PROBLEMAS DE SENSIBILIDAD (Gp:) a (Gp:) b (Gp:) DE = hn Ley de
distribución de Boltzmann

8 2.2. Niveles poblacionales, 2 UV IR RMN DE DE DE Se muestra
aquí la diferencia de energía entre los distintos
estados energéticos que dan lugar a las distintas
espectrocopias.

9 (Gp:) Irradiación con absorción de hn (Gp:)
Irradiación con absorción de hn (Gp:) a (Gp:) b DE
A favor del campo Contra el campo Estado aa (Gp:) Polo
magnético (Gp:) Polo magnético (Gp:) B0 (Gp:) a
(Gp:) a (Gp:) Polo magnético (Gp:) Polo magnético
(Gp:) B0 (Gp:) b (Gp:) a (Gp:) a (Gp:) b (Gp:) Estado ab 2.3. El
proceso de la resonancia, 1

10 RELAJACIÓN DE ESPÍN (Gp:) a (Gp:) b (Gp:) a
(Gp:) b (Gp:) a (Gp:) b El retorno al equilibrio se denomina
RELAJACIÓN 2.3. El proceso de la resonancia, 2 Pulso de
radiofre-cuencia relajación Cuando se deja de aplicar el
pulso, el vector magnetización tiende a recuperar su
posición de equilibrio mediante un proceso de
relajación (emite la energía absorbida). Este
proceso de relajación da lugar a la FID, que es una onda
sinusoidal exponencialmente amortiguada. Esto es lo que se
denomina caída libre de inducción (FID, free
induction decay).

11 Tres requerimientos esenciales: Un campo magnético (Bo)
homogéneo e intenso Una fuente de radiación de
radiofrecuencia (B1) para excitar los núcleos de la
muestra Un método para detectar la señal de RMN
(Gp:) El campo magnético es suministrado por: Imán
permanente Electroimán Bobina superconductora (Gp:) 60-90
MHz (Gp:) 100-850 MHz (Gp:) Bobina superconductora
Espectrómetro de RMN, 1

12 Antiguamente (1950-70) ONDA CONTINUA Actualmente (desde 1970)
TECNICA DE PULSOS (FT) Espectrómetro de RMN, 2

13 Espectrómetro de RMN, 3 El solenoide es superconductor
sólo a muy bajas temperaturas, por eso se encuentra
rodeado de He líquido (T = 4 K), para evitar que el He se
evapore rápidamente, está protegido por alrededor
por N2 líquido (T = -196 oC)

14 Espectrómetro de RMN, 4 Diagrama de la
adquisición de un espectro de RMN:
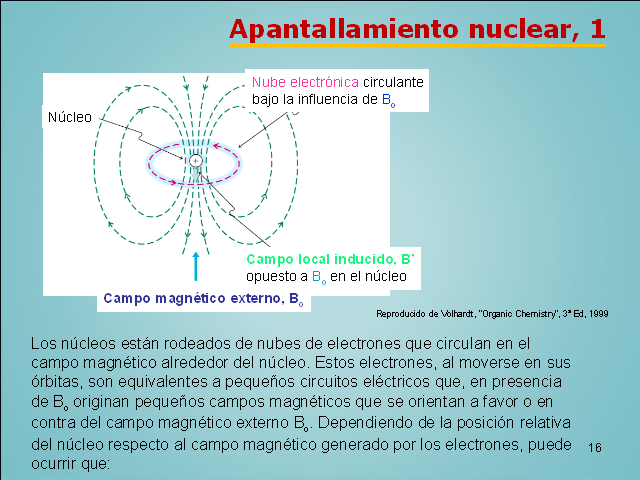
15 (Gp:) Nube electrónica circulante bajo la influencia de
Bo (Gp:) Campo magnético externo, Bo (Gp:) Núcleo
(Gp:) Campo local inducido, B’ opuesto a Bo en el
núcleo Apantallamiento nuclear, 1 Reproducido de Volhardt,
“Organic Chemistry”, 3ª Ed, 1999 Los
núcleos están rodeados de nubes de electrones que
circulan en el campo magnético alrededor del
núcleo. Estos electrones, al moverse en sus
órbitas, son equivalentes a pequeños circuitos
eléctricos que, en presencia de Bo originan
pequeños campos magnéticos que se orientan a favor
o en contra del campo magnético externo Bo. Dependiendo de
la posición relativa del núcleo respecto al campo
magnético generado por los electrones, puede ocurrir
que:

16 Apantallamiento nuclear, 2 Bnúcleo = Bo +
B’electrones (Gp:) Nube electrónica circulante bajo
la influencia de Bo (Gp:) Campo magnético externo, Bo
(Gp:) Núcleo (Gp:) Campo local inducido, B’ opuesto
a Bo en el núcleo (Gp:) Efecto Núcleo
Bnúcleo < Bo Diamagnético Apantallado
Bnúcleo > Bo Paramagnético Desapantallado (Gp:)
Bo (Gp:) B’e (Gp:) Bo (Gp:) B’e

17 (Gp:) 480 Hz (Gp:) 320 Hz Apantallamiento nuclear, 3
Reproducido de Volhardt, “Organic Chemistry”, 3ª
Ed, 1999 (Gp:) ?? B ?? (Gp:) Bo = 2.1 Tesla Para Bo = 2.1 T no =
90.000.000 Hz (1H resuena a 90 MHz) TMS (Ref) En un espectro de
RMN no se representan frecuencias absolutas de resonancia, porque
darían lugar a números demasiado altos. Para
evitarlo, se elige una señal como referencia y lo que se
determina es la separación entre la frecuencia de
resonancia de un núcleo y una frecuencia de referencia.
Esta magnitud se mide en Hz.

18 Apantallamiento nuclear, 4 Se trabaja con la diferencia
respecto a una referencia (nseñal – nref) (Gp:)
Problema: dependencia de n de Bo Solución: dividir por no
(n aparato) (nseñal – nref) no (Gp:) Para Bo = 2.1 T
no = 90.000.000 Hz 480 / 90.000.000 = 5.33 x 10-6 (Gp:) Para Bo =
4.2 T no = 180.000.000 Hz 960 /180.000.000 = 5.33 x 10-6 (Gp:)
Problema: números muy pequeños Solución:
multiplicar por 106 (ppm) (nseñal – nref) no (Gp:) ?
106 (Gp:) d = (Gp:) ClCH2OCH3 (Gp:) 480 Hz (Gp:) 320 Hz (Gp:) Bo
(T) 2.1 4.2 960 Hz 640 Hz (Gp:) Tetrametilsilano (TMS) (Gp:)
REFERENCIA INTERNA:

19 Desplazamiento químico, 1 (Gp:) (nseñal –
nref) no (Gp:) ? 106 (Gp:) d = Desplazamiento químico (d)
: Posición de una señal en el espectro Se expresa
en función de la de una sustancia de referencia (Gp:) n
depende de la envoltura electrónica n depende de la
estructura Como patrón se utiliza TETRAMETILSILANO (TMS)
Ventajas del TMS : 1) Señal única 2) Líquido
volátil 3) Aparece a n < n señales (n TMS = 0
ppm) 4) No interacciona con la muestra Partes por millón
(ppm)

20 (Gp:) 480 Hz (Gp:) 320 Hz (Gp:) ?? B ?? (Gp:) Bo = 2.1 Tesla
Para Bo = 2.1 T no = 90.000.000 Hz (1H resuena a 90 MHz) TMS
(Ref) 5.33 ppm 3.55 ppm ¡ Observa: 1 ppm = 90 Hz !
Desplazamiento químico, 2

21 0 1 2 3 4 5 6 7 8 d (1H) ppm TMS MeCN Me2CO Me2SO C6H6 (Gp:)
(n) (Gp:) (d) (Gp:) APANTALLAMIENTO (Gp:) Desapantallado (Gp:)
apantallado (Gp:) A medida que el núcleo está
más apantallado (como consecuencia de su entorno
electónico) el campo magnético efectivo que percibe
es menor y por tanto resuena a menor frecuencia, es decir,
aparece a menor desplazamiento químico en el espectro.
Desplazamiento químico, 3

22 El desplazamiento químico de un protón depende
de su entorno, y aquí se muestran los desplazamientos
químicos aproximados para distintos tipos de compuestos.
El desplazamiento químico depende, entre otros factores,
del grado de sustitución y de la electronegatividad de los
sustituyentes. Así, hay diferencias entre protones de
grupos alquilo primarios, secundarios o terciarios. Afecta
también la electronegatividad del sustituyente al que
está unido el protón y la distancia al sustituyente
electronegativo. Hay casos muy interesantes como los de los
protones aromáticos, vinílicos y
aldehídicos, en los que el desplazamiento químico
tiene valores anormalmente altos… Desplazamiento
químico, 4

23 Desplazamiento químico, 5

Campo externo, B0 Blocal (Gp:) Blocal Blocal (Gp:) Blocal
ALQUENOS Desplazamiento químico, 6 La circulación
de los electrones ? origina un campo inducido que se suma al
campo externo Bo en la zona ocupada por los protones y
éstos resuenan a frecuencias más altas, mostrando
valores de desplazamiento químico, entre 5 y 6 ppm. La
distribución de la densidad electrónica alrededor
de los enlaces no es simétrica y el desplazamiento
químico de los núcleos vecinos dependerá de
su posición relativa con respecto a ella. Este efecto
anisótropo generado por la circulación de
electrones en átomos vecinos se da fundamentalmente en
moléculas con electrones ?. 24

25 Factores de los que depende d 1. Grado de sustitución
2. Electronegatividad del sustituyente (desprotección
magnética local) 3. Distancia del sustituyente 4.
Presencia de dobles y/o triples enlaces (anisotropía
magnética local) 5. Interacciones intermoleculares:
puentes de hidrógeno, disolvente, etc. (Gp:) CH3X EN (X) d
(ppm) CH3F 4.0 4.26 CH3OH 3.4 3.40 CH3Cl 3.2 3.05 CH3Br 3.0 2.68
CH3I 2.7 2.16 CH3H 2.2 0.23 (Gp:) d aumenta con la EN del
sustituyente (Gp:) Desprotección magnética local
Desplazamiento químico, 7 Un efecto – I producirá
un desapantalla-miento y un aumento del valor de desplazamiento
químico (Gp:) alcanos (Gp:) alquinos (Gp:) alquenos (Gp:)
d 1. Grado de sustitución 2. Electronegatividad del
sustituyente

26 ALQUENOS ALDEHIDOS Desplazamiento químico, 8
Hidrógenos olefínicos: desplazamiento
químico (d): 5 – 6 ppm Hidrógeno de
aldehído: desplazamiento químico (d): 9 – 10 ppm El
hidrógeno de aldehído está aún
más desapantallado que los olefínicos y
aromáticos. La razón es que el H aldehídico
está desprotegido tanto por la circulación de los
electrones en el doble enlace, como por el efecto atractor de
electrones del oxígeno.

27 AROMÁTICOS Campo externo, B0 (Gp:) Blocal (Gp:) Blocal
Corriente de anillo (Gp:) Blocal (Gp:) Blocal Desplazamiento
químico, 9 El campo magnético Bo induce una
corriente circular a través de los orbitales p del anillo
aromático. Dicha corriente (corriente de anillo) induce un
campo magnético que se opone al campo externo Bo en el
centro del anillo. Los átomos de hidrógeno unidos
directamente al anillo aromático se encuentran en la zona
donde el campo magnético generado por los electrones se
suma al externo, por lo que éstos resultan
desapantallados. H del benceno: desplazamiento químico
(d): 7.3 ppm aprox.

28 ALQUINOS Desplazamiento químico, 10 El acetileno es una
molécula lineal, la nube de electrones ? que constituye el
triple enlace tiene una simetría axial alrededor del eje
de la molécula y en presencia de un campo magnético
externo,orientado en la dirección del eje de la
molécula, la circulación de electrones ? origina un
campo magnético que se opone al exterior en la
posición que ocupan los protones, por lo que éstos
resultan apantallados (efecto diamagnético, resuenan a
menor frecuencia).

29 10 9 8 7 6 5 4 3 2 1 0 COOH Ar–OH R–OH R–NH
R–CHO Ar–H C?CH C?CH C?CH–CHn CO–CHn
Ar–CHn Hal–CHn O–CHn N–CHn C–CHn
TMS (Gp:) Aromático (Gp:) Olefínico (Gp:)
Alifático Desplazamiento químico, 11

30 Protones equivalentes Protones equivalentes son los que
están en el mismo entorno químico y originan una
única señal en el espectro de 1H-RMN. En este caso
los protones del Me del metanol originan los tres la misma
señal, el protón unido al átomo de
oxígeno sale a mayor d.

31 La integral de una señal es proporcional al
número de núcleos equivalentes que la originan
Integral = área total del pico Protones equivalentes.
Integral, 1

32 La integral de una señal es proporcional al
número de núcleos equivalentes que la originan
Integral = área total del pico Protones equivalentes.
Integral, 2

33 EL ESPECTRO DEL ETANOL Reproducido de P.J. Hore,
“Nuclear Magnetic Resonance”, OCP, 1995 30 MHz (Gp:)
400 MHz (Gp:) Reproducido de D. Canet, “Nuclear Magnetic
Resonance”, Wiley, 1996 6. Acoplamiento spin-spin El campo
magnético que rodea a los núcleos está
influído por el resto de los momentos magnéticos de
la molécula, como son los de otros núcleos vecinos.
Así, si un protón debería dar una
señal a una frecuencia correspondiente a su d, esta
señal puede aparecer desdoblada en varias dependiendo de
la orientación magnética de los núcleos
vecinos.

34 dX dA n (frecuencia) JAX JXA (Gp:) JAX = JXA J = constante de
acoplamiento. Se mide en (Hz) J no depende del campo
magnético aplicado Bo, sino de la relación entre
los núcleos (mismo valor en cualquier aparato) Doblete
Doblete 6. Acoplamiento spin-spin. Constante de acoplamiento
(J)

35 Cuando el protón Ha cercano está alineado y en
el mismo sentido del campo magnético externo, desapantalla
a Hb. Cuando Ha está alineado en contra del campo,
apantalla a Hb. La señal para los protones Hb se
acoplará en picos de la misma altura (doblete). La
absorción Ha está afectada por tres combinaciones
de espines Hb: Si los protones Hb refuerzan el campo externo,
esto desapantallará a Ha. Si un Hb está alineados
en contra del campo y el otro Hb refuerza el campo, el efecto se
cancelará. Si los protones Hb están en contra del
campo externo, esto apantallará a Ha . La señal de
Ha será un triplete (relación 1:2:1). 6.
Acoplamiento spin-spin. Constante de acoplamiento (J) DOBLETE
TRIPLETE

36 (Gp:) JA,X (Gp:) JA,X (Gp:) nA (Gp:) nx (Gp:) DnA,X (Gp:)
Origina espectros de PRIMER ORDEN (Gp:) DnA,X >> JA,X (Gp:)
JA,B (Gp:) nA (Gp:) nB (Gp:) DnA,B (Gp:) JA,B (Gp:) Origina
espectros COMPLEJOS (Gp:) DnA,B ? JA,B (Gp:) 1) ACOPLAMIENTO
DÉBIL (Gp:) 2) ACOPLAMIENTO FUERTE Acoplamiento spin-spin.
Espectros de PRIMER ORDEN

37 6. Acoplamiento spin-spin. Constantes de acoplamiento (J) El
valor de J, que depende de distintos factores en especial del
tipo de hibridación de los átomos implicados,
disminuye con el número de enlaces: 2J = 12-15 Hz 3J = 6-8
Hz

38 Constantes de acoplamiento

39 Reglas de desdoblamiento Válidas para espectros de
primer orden Dd (Hz) >10 JA,X Los núcleos equivalentes
no se acoplan entre sí. El acoplamiento con n
núcleos equivalentes origina un desdoblamiento en (2nI+1)
líneas. En el caso del protón, I = 1/2 por tanto el
acoplamiento con n núcleos equivalentes origina un
desdoblamiento en (n +1) líneas. Todas las líneas
de un multiplete están igualmente separadas. La
separación corresponde al valor de la constante de
acoplamiento. La intensidad relativa de las líneas de un
multiplete viene dada por el triangulo de Pascal.

ESTA PRESENTACIÓN CONTIENE MAS DIAPOSITIVAS DISPONIBLES EN
LA VERSIÓN DE DESCARGA