Determinantes Álgebra Lineal

Objetivos

OBJETIVO GENERAL:

Conocer a fondo la determinante de una matriz,
entendiendo sus propiedades, aplicaciones, historia
bibliográfica de los principales a portadores al estudio
de estas y métodos de resolución.

OBJETIVOS ESPECIFICOS:

• Conocer la definición de la
  función determinante.

• Calcular determinantes de matrices de 2×2; 3×3 y de
  mayor tamaño.

• Conocer las propiedades para facilitar el
  cálculo de determinantes de cualquier tipo de matriz
  cuadrada.

• Determinar distintas fórmulas para calcular
  determinantes de cualquier orden.

• Conocer una forma para multiplicar dos determinantes
  de manera directa, es decir, sin calcular previamente el
  determinante de una matriz.

• Calcular la inversa de una matriz cuadrada por el
  método de determinantes y adjuntas.

• Calcular el determinante de una matriz
  transpuesta

• Aplicar la Regla de Cramer para la resolución
  de sistemas de ecuaciones lineales.

• Utilizar determinantes para facilitar el
  cálculo de áreas y volúmenes.

Introducción
biográfica

Los determinantes se introdujeron en el occidente en el
siglo XVI, estos fueron antes que las matrices que no aparecieron
hasta el siglo XIX. Algunos de los más grandes
matemáticos ayudaron al desarrollo de las propiedades de
los determinantes. La mayoría dice que el estudio de los
determinantes se empezó con Leibniz ya que el empleo los
determinantes con relación a los sistemas de ecuaciones
lineales simultaneas. Pero las contribuciones más
productivas a la teoría de los determinantes fueron las
del matemático francés Augustín-Louis Cauchy
(1789-1857), fue un escritor potente ya que publico casi 800
artículos. Sus contribuciones al estudio de las
matemáticas fueron revolucionarias, él fue el
primero en definir los conceptos de límites y continuidad
así como el de convergencia de una serie infinita.
Además de fundar la teoría de los números
complejos, la teoría de la probabilidad, geometría,
teoría de la propagación de ondas; contribuyo a la
teoría de determinantes y de ecuaciones
diferenciables.

Hay algunos otros matemáticos que deben ser
nombrados aquí. El desarrollo de un determinante por
cofactores fue empleado por primera vez por el matemático
francés Pierre de Laplace (1749-1827).

Un contribuyente principal de la teoría de los
determinantes estando solo Cauchy antes que él fue el
matemático alemán Carl Gustav Jacobi
(1804-1851).Fue con él con quien la palabra determinante
ganó la aceptación definitiva. Lo primero en lo que
Jacobi empleo los determinantes fue en la funciones, al
establecer la teoría de las funciones de varias variables,
Sylvester llamó más tarde jacobiano a este
determinante.

En su sentido original, el determinante determina la
unicidad de la solución de un sistema de ecuaciones
lineales. Fue introducido para el caso de orden 2 por Cardano en
1545 en su obra Ars Magna presentado como una regla para la
resolución de sistemas de dos ecuaciones con dos
incógnitas. Esta primera fórmula lleva el nombre de
regula de modo.

El japonés Kowa Seki introdujo los determinantes
de orden 3 y 4 en la misma época que el alemán
Leibniz.

La aparición de determinantes de órdenes
superiores tardó aún más de cien años
en llegar. Curiosamente el japonés Kowa Seki y el
alemán Leibniz otorgaron los primeros ejemplos casi
simultáneamente.

Leibniz estudió los distintos tipos de sistemas
de ecuaciones lineales. Al no disponer de la notación
matricial, representaba los coeficientes de las incógnitas
con una pareja de índices: así pues escribía
ij para representar ai, j. En 1678 se interesó por un
sistema de tres ecuaciones con tres incógnitas y obtuvo,
para dicho ejemplo, la fórmula de desarrollo a lo largo de
una columna. El mismo año, escribió un determinante
de orden 4, correcto en todo salvo en el signo.1 Leibniz no
publicó este trabajo, que pareció quedar olvidado
hasta que los resultados fueron redescubiertos de forma
independiente cincuenta años más tarde.

En el mismo periodo, Kowa Seki publicó un
manuscrito sobre los determinantes, donde se hallan
fórmulas generales difíciles de interpretar. Parece
que se dan fórmulas correctas para determinantes de
tamaño 3 y 4, y de nuevo los signos mal para los
determinantes de tamaño superior.2 El descubrimiento se
queda sin futuro a causa del cierre de Japón al mundo
exterior por órdenes del shogun, lo que se ve reflejado en
la expulsión de los Jesuitas en 1638.

Definición de
la función determinante

El determinante es una herramienta matemática, se
puede encontrar o extraer un determinante únicamente de
las matrices que son cuadradas (tienen igual número de
filas y columnas), y es un numero real (en caso de que la matriz
sea real) consistente en la suma de los productos elementales de
la matriz.

El orden de un determinante viene dado por el
número de filas y columnas que tenga. Existen diferentes
métodos para resolverlos, que veremos a
continuación.

Nota: Es necesario indicar que usaremos los
símbolos Det(A) o │A│ para referirnos al
determinante de A.

El determinante de una matriz puede ser positivo, negativo o
cero.

PROPIEDADES DE LOS DETERMINANTES:

1. El determinante de una matriz
cuadrada coincide con el determinante de su traspuesta, es
decir: 

2. Si intercambiamos dos filas o dos
columnas de una matriz cuadrada, su determinante cambia de signo
aunque son iguales en valor absoluto.

3. Si  multiplicamos todos los
elementos de una fila o columna de una matriz cuadrada por un
número  k, su determinante queda multiplicado por
dicho número.

Como generalización de esta propiedad, si
multiplicamos todos los elementos de una matriz cuadrada de
orden  n  por un número  k, su determinante
queda multiplicado por  kn, es decir: Det (k. A) = kn.
Det (A).

4. El determinante del producto de dos
matrices cuadradas del mismo orden es igual al producto de los
determinantes de dichas matrices: Det (A. B) = Det (A)* Det
(B).

5. Si una matriz cuadrada tiene todos
los elementos de una fila o columna nulos, su determinante es
cero.

 6. Si una matriz cuadrada tiene
dos filas o dos columnas iguales su determinante es
cero.

7. Si una matriz cuadrada tiene dos
filas o columnas proporcionales su determinante es
cero.

8. Si todos los elementos de una fila o
columna de una matriz cuadrada se descomponen en dos sumandos,
entonces su determinante es igual a la suma de dos determinantes
que tienen en dicha fila o columna el primero y el segundo
sumando respectivamente, siendo los restantes elementos iguales a
los del determinante inicial.

9. Si una fila o columna de una matriz
cuadrada es combinación lineal de dos o más de las
restantes filas o columnas, su determinante es cero.

10. Si a una fila o columna de una
matriz cuadrada se le suma otra paralela a ella, su determinante
no varía.

11. Si a una fila o columna de una
matriz cuadrada se le suma otra paralela a ella multiplicada por
un número, su determinante no varía.

4.-CALCULO DE DETERMINANTES POR
PROPIEDADES:

1) Comprobar en la siguiente matriz que
detA = detAt

Solución:

Desarrollamos por cofactores eliminando la primera
columna:

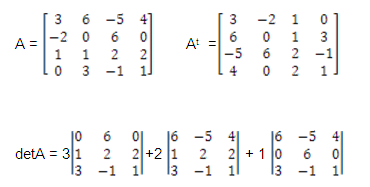
Estas matrices de 3×3 las resolvemos por el
método de sarrus.

detA = 3(0+36-6) + 2(12-30-4-24+12+5) +
(36-72)

detA = 90 + 2(-29) – 36 = – 4

De la misma forma aplicamos cofactores para eliminar la
segunda columna de la matriz transpuesta.

Las matrices de 3×3 las resolvemos por
sarrus.

detAt = 2( 12 – 30 – 4- 24 + 12 + 5) – 6( 3
+ 12 – 18 – 6)

detAt = 2(- 29 ) – 6(-9)

detAt = – 4

Conclusión: Hemos demostrado así que detA
= detAt

2) Encuentre el determinante de la
matriz transpuesta si:

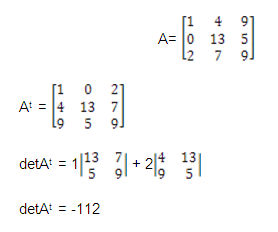
3) Por reducción de la segunda
fila encuentre el determinante de la matriz transpuesta
si:

4) Demuestre que si intercambiamos dos
filas de una matriz su determinante varia en el signo.

5) Compruebe que si A es una matriz
cuadrada con una columna de ceros, su determinante es
cero.

Conclusión: De esta forma hemos llegado a
demostrar que si una matriz tiene una fila o columna de ceros su
determinante siempre será cero.

6) Compruebe que detA = 0, si A es una
matriz cuadrada con dos filas iguales.

7) Compruebe que detA = 0 si la
terceracolumna es proporcional a la primera columna.

8) Aplicando las propiedades de los
determinantes, evaluar el determinante de:

9) Aplicando las propiedades de los
determinantes encuentre el determinante de:

10) Aplicando las propiedades de los
determinantes encontrar el determinante de A.

11) Evalúe el determinante de la
siguiente matriz, aplicando las propiedades de los
determinantes

12) Aplicando las
propiedades de los determinantes reduzca los siguientes
determinantes a determinantes de menor orden y
resuélvalos.

13) Encuentre los
determinantes de las siguientes matrices:

14) Encontrar el
determinante si:

15) Encontrar el
determinante de las siguientes matrices aplicando la propiedad
#4

16) Encontrar el
determinante de la matriz y de su transpuesta si A es una matriz
formada por números complejos.

17) Desarrollar aplicando
la propiedad 3

18) Desarrollar aplicando
la propiedad 4.

19) Aplicar la propiedad
5.

20) Aplicar la propiedad 7.

La tercera fila es combinación lineal de la
primera entonces |A|=0

21)Aplicando la propiedad 8 y 6
obtenemos la propiedad 9

22) Resolver aplicando la propiedad
7.

23) Resolver aplicando la propiedad
6.

24) Encontrar el determinante aplicando
la propiedad 8.

Fórmulas para
desarrollar determinantes

5.1.- DETERMINANTES DE PRIMER
ORDEN:

El determinante de una matriz de primer orden se define
simplemente como el elemento de la matriz. Por ejemplo, si A=[3]
, entonces det(A)= 3

[a11]=a11

5.2.- DETERMINANTES DE SEGUNDO
ORDEN:

Una matriz de orden 2×2 está dada por la
diferencia de los productos de las dos diagonales de la
matriz.

• EJEMPLO 1:

Encuentre el determinante de la matriz
siguiente:

• EJEMPLO 2:

Encuentre el determinante de la siguiente
matriz:

• EJEMPLO 3:

Encuentre el determinante de la siguiente
matriz:

5.3.- DETERMINANTES DE TERCER ORDEN:

Para resolver determinantes de tercer orden aplicaremos
dos procesos que seconocen como: La Regla de Sarrus y el
Método de la Estrella:

5.3.1.- REGLA DE SARRUS:

La regla de sarrus es de fácil
memorización para calcular el determinante de una matriz
de 3×3. Lleva este nombre en honor a su inventor el
matemático francés Pierre Frederic
Sarrus.

Ahora consideremos la siguiente matriz:

Su determinante se puede calcular de la siguiente
manera:

• 1) Aumentamos las dos primeras columnas de la
  matriz a la derecha de esta matriz y asi ahora quedaran cinco
  columnas.

• 2) Sumamos el producto de las diagonales
  descendientes, y restamos el producto de las diagonales
  ascendiente estas son:

(a11x a22 a33) + (a12 x a23x a31) + (a13 x a21 xa32)
– (a12 x a21 x a33) – (a11 x a23 x a32) – (a13
x a22 x a31)

También podemos resolvereste determinante por el
método de la estrella:

5.3.2.- METODO DE LA ESTRELLA:

Los términos con signo + están formados
por los elementos de la diagonal principal y los de las
diagonales paralelas con su correspondiente vértice
opuesto.

5.4.- DETERMINANTES DE CUALQUIER
ORDEN:

5.4.1.-METODO DE GAUSS:

Para calcular con este método primero definiremos
lo siguiente:

• Determinante de una matriz triangular:

Si A es una matriz triangular de orden n, entonces su
determinante es el producto de los elementos de la diagonal
principal, es decir;

detA = a11 x a22 x
a33…….xann

Ahora continuamos con el concepto anterior:

Se conoce como método de Gauss a un método
para facilitar el cálculo de determinantes usando la
propiedad de estos. Dicho método consiste en hallar un
determinante equivalente (con el mismo valor) al que se pretende
calcular, pero triangular. De esta forma el problema se reduce a
calcular un determinante de una matriz triangular, caso que es
fácil usando las propiedades de los
determinantes.

Para conseguir triangulizar el determinante se puede
aplicar las siguientes operaciones:

1.- Permutar do filas o columnas.

2.- Multiplicar o dividir una línea por un
número no nulo.

3.- Sumarle o restarle a una línea otra paralela
multiplicada por un número no nulo.

Aplicando todas estas operaciones llegamos a la
siguiente matriz:

5.4.2.- METODO DE MENORES Y
COFACTORES:

DEFINICION DE LOS MENORES Y COFACTORES DE UNA
MATRIZ:

Si A es una matriz cuadrada, entonces el menor del
elemento aij se denota por Mij y se define como el determinante
de la submatriz que queda después de quitar el
i-ésimo renglón y la j-ésima columna de A.
El numero (–1)i+jMij se denota por Cij y se denomina
cofactor del elemento aij.

• EJEMPLO 1:

Observemos que

• EJEMPLO 2:

Encuentre todos los menores y cofactores de:

Solución:

Para encontrar el menor M11, se elimina el primer
renglón y la primera columna de A y se evalúa el
determinante de la matriz resultante.

El determinante de una matriz Anxn es igual a la suma de
los productos obtenidos multiplicando los elementos decualquier
fila o columna por sus respectivos cofactores respetando las
reglas ya vista anteriormente.

En este caso está desarrollada la primera
columna, pero puede ampliarse este método para cualquier
fila o columna, siempre y cuando se respeten el patrón de
signos de los cofactores.

• EJEMPLO 2:

Evaluar det (A) por desarrollo por cofactores a lo largo
de la primera columna de A.

Solución:

5.4.3.- ELIMINACION CONTINUA:

Este método fue visto en clases, y consiste que
en cada matriz que se vaya obteniendo al reducir una variable se
la debe ir dividiendo para el elementoprincipal elevado a la(n-2)
donde n es el orden de cada matriz que se vaya
obteniendo.

Ejemplo:

Encontrar el determinante por medio de
eliminación continua:

5.5.- EJERCICIOS:

1) Calcular el determinante de la siguiente
matriz:

Det(A) = 5 x 6 = 30

2) Por el método de Gauss hallar el
siguiente determinante:

Det F = 275

• 3)  Por la regla de sarrus hallar el
  determinante de la siguiente matriz:

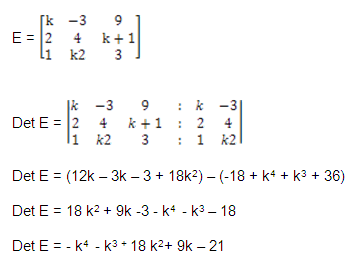
• 4)  Por el método de la estrella hallar
  el siguiente determinante:

Det(A) = [(8x4x2) + (-3x7x-1) + (2x-6×1) –
(1x4x-1) – (-3x2x2) – (7x-6×8)]

Det(A) = 64 + 21 – 12 +4 + 12 +336

Det(A) = 425

• 5)  Calcular el determinante de B.

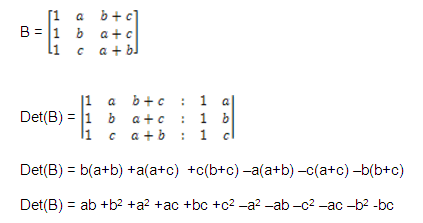
Det(B) = 0

• 6)  Encontrar el determinante por medio de
  eliminación continua:

• 7) Use el método de los cofactores para
  encontrar el determinante de la siguiente matriz:

• 9) Por reducción de la segunda fila
  resuelva el siguiente determinante:

• 10) En el ejercicio anterior encuentre el
  determinante eliminando la segunda columna.

6.-PRODUCTO DE DETERMINANTES.

Teorema de Cauchy: El producto de dos
determinantes semejantes se puede poner en forma de una
determinante semejante a los factores y cuyos elementos sean las
sumas de los productos de los elementos de una línea de un
factor, por los elementos correspondientes de otra línea
del otro factor.

Sean para la sencillez del segundo grado sabiendo que lo
que se demuestre en este caso es general para todos; lo que se
quiere probar es que:

6.1.- EJERCICIOS:

• 1) Multiplicar filas por filas, y filas por
  columnas, comprobar el resultado.

• 2) Dividir las siguientes matrices:

• 3) Elevar al cuadrado la siguiente
  determinante:

• 4) Elevar al cubo la siguiente
  determinante:

• 5) Halle el producto
  de:

• 6) Hallar 3A+2C2 si se sabe que:

7.-DETERMINANTES DE ORDEN N-SIMO

El símbolo:

Este símbolo es una forma abreviada de expresar
el polinomio construido por la suma algebraica de todos los
productos posibles, cada uno de n factores de manera
que:

1)En cada producto figura solamente un elemento de cada
fila y uno solo de cada columna habrá por lo tanto n!
productos.

2)El signo de cada producto es positivo o negativo
,según que el numero de inversiones de los
subíndices sea par o impar, después de haber
colocado las letras en el orden en el que figuran en la primera
fila.

La suma algebraica así obtenida se denomina
desarrollo o valor del determinante. Cada producto, con su signo,
recibe el nombre de término del desarrollo del
determinante.

Un determinante de orden n se representa también
por

Con esta notación cada elemento se caracteriza
por dos subíndices, el primero indica la fila y el segundo
la columna a la que pertenece o donde se encuentra. Así,
pues a23 es el elemento de la segunda fila y la tercera
columna.

La diagonal principal de un determinante está
formado por los elementos de la matriz situados sobre la recta
que une el primer elemento de la primera fila con el
último de la ultima fila.

CALCULO DE DETERMINANTES DE ORDEN
N-ESIMO

Consiste en conseguir que una de las
líneas del determinante esté formada por elementos
nulos, menos uno: el elemento base o pivote, que
valdrá 1 ó -1.

Para esto haremos lo siguiente:

• 1. Si
  algún elemento del determinante vale
  la unidad, se elige una de las dos líneas:
  la fila o la columna, que contienen a dicho elemento (se
  debe escoger aquella que contenga el mayor número
  posible de elementos nulos).

2. En caso negativo:

8.- DETERMINANTE DE LA MATRIZ INVERSA DE
UNA MATRIZ NOSINGULAR:

8.1.- EJERCICIOS:

• 11)  Encuentre la inversa de la
  siguiente matriz:

• 12)  Encuentre la inversa de la
  siguiente matriz:

La matriz no es inversible

• 14) Encuentre el determinante de
  B(inversa)

• 15) Hallar la matriz inversa de:

9.-DETERMINANTE DE UNA MATRIZ
TRANSPUESTA

Si A es una matriz cuadrada entonces es cierto
que:

9.1.- EJERCICIOS:

En los siguientes ejercicios encuentre el determinante
de la matriz y de su transpuesta.

• 1) Hallar w(transpuesta) y su
  determinante y demostrar que W=a su transpuesta
  volviéndola a transponer.

10.- ADJUNTO DE UNA
MATRIZ

Ejemplo:

La traspuesta de la matriz de los
cofactores anteriores proporciona el adjunto
de A:

Observemos que esta propiedad nos permite
hallar por otro método la inversa de una
matriz.

 Ejemplo:

 Consideremos la matriz

Ejercicio:

 Calcular, por la propiedad anterior,
la inversa de las siguientes matrices:

a) Primero hallaremos el
determinante de la matriz A:

El siguiente paso es hallar el adjunto de
la matriz B, así pues, los cofactores de los
cuatro elementos de B son:

La traspuesta de la matriz de los
cofactores anteriores proporciona el adjunto
de A:

APLICACIONES DE LOS DETERMINANTES: OBTENCION DE LA
INVERSA DE UNA MATRIZ:

Si A es una matriz invertible de nxn, entonces es cierto
que:

A continuación daremos a conocer como se obtiene
la adjunta de una matriz:

Al inicio de este capítulo ya dimos a conocer
como se obtiene los cofactores de una matriz, ya que necesitamos
este concepto para definir la adjunta de una matriz, y
está definida por:

La adjunta de una matriz es igual a los cofactores
transpuestos de la matriz.

10.1.- EJERCICIOS:

1) Obtenga la inversa de una matriz aplicando
determinantes:

• 7) Hallar la matriz
  inversa:

Aplicaciones de los
determinantes: regla de Cramer

La regla de Cramer llamada así por su inventor
Gabriel Cramer (1704-1752), matemático suizo, aunque
Cramer no está considerado al lado de los grandes
matemáticos de su tiempo, sus contribuciones como
diseminador de las ideas matemáticas le ganaron un bien
merecido lugar en la historia de las
matemáticas.

La siguiente regla proporciona una forma útil
para la solución de ciertos sistemas lineales den
ecuaciones con n incógnitas. Esta fórmula,
denominada Regla de Cramer es de interés marginal para
efectos de cómputo, aunque es útil para estudiar
las propiedades matemáticas de una solución sin
necesidad de resolver el sistema.

Regla de Cramer:

12.1.- EJERCICIOS:

Aplicar la regla de Cramer para resolver los siguientes
ejercicios:

Como la tercera fila es combinación lineal de las
otras dos entonces la solución de este sistema es
infinitas soluciones porque el determinante es cero.

La solución de este sistema es infinitas
soluciones por tener el determinante igual a 0.

Aplicaciones de los
determinantes: obtención de áreas, volúmenes
y ecuaciones de rectas y planos

13.1.- ÁREA DE UN TRIANGULO EN EL PLANO
XY:

El área de un triangulo cuyos vértices son
(x1, y1), (x2, y2), (x3, y3) está dada por:

El signo (±) se obtiene para obtener un
área positiva.

13.1.2.- PRUEBA PARA DETERMINAR SI TRES PUNTOS EN EL
PLANO XY SON COLONIALES:

Tres puntos (x1, y1), (x2, y2), (x3, y3) son colineales
si y solo si:

13.2.- ÁREA DE LOS
POLÍGONOS:

Con el resto de polígonos primero tenemos que
dividirlos en varios triángulos, crear el determinante y
sumar todos los resultados parciales de los
determinantes.

13.2.1.- ECUACIÓN DE LA RECTA QUE PASA POR LOS
PUNTOS (X1, Y1) Y (X2, Y2) EN EL PLANO XY:

La ecuación de la recta que pasa por los puntos
distintos (x1, y1) y (x2, y2) está dada por:

• Ejemplo:

Encuentre la solución de la recta que pasa por
los puntos (2, 4), (-1, 3)

13.3.- VOLUMEN DE UN TETRAEDRO:

El volumen de un tetraedro cuyos vértices son
(x1, y1, z1), (x2, y2, z2), (x3, y3, z3) y (x4, y4, z4)
está dado por:

13.3.1.- PRUEBA PARA DETERMINAR PUNTOS COPLANARES EN
EL ESPACIO:

Cuatro puntos (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) y
(x4, y4, z4) son coplanares si y solo si:

13.4.- EVALUACIÓN DE UN PLANO FORMADO POR TRES
PUNTOS:

La ecuación del plano que pasapor
los puntos (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) está
dada por:

13.5.- EJERCICIOS:

1) Encuentre el área del triangulo que tiene
como vértices A(-3,2) B(5,-1) C(2,4)

Solución:

2)Compruebe que estos puntos son colineales:

A(1,2) B(3,4) C(5,6)

Como el determinante es cero entonces los tres puntos si son
colineales.

3) Encuentre la solución de la recta que pasa
por los puntos dados:

A(-2,3) B(-2,-4)

4) Encuentre el volumen del tetraedro que tiene los
vértices dados:

(0,4,1) (4,0,0) (3,5,2) (2,2,5)

5)Determine si los puntos dados son coplanares:
(0,0,-1); (0,-1,0); (1,1,0); (2,1,2)

6)Encuentre una ecuación del plano que pase por
los puntos dados:

(1,2,7); (4,4,2); (3,3,4)

Conclusiones

En el primer punto del trabajo tuvimos un concepto
general de lo que son los determinantes y varios conceptos y
aplicaciones previas para determinarlos como son los menores, los
cofactores, entre otros.

Demostramos también todas las propiedades de los
determinantes con los cuales nos facilitan mucho el trabajo y nos
ayuda a terminar más rápido el proceso
aplicado.

Las diferentes formas de resolución nos
llevó a un enfoque mucho más amplio en la
resolución del determinante, por ejemplo el método
de cofactores se usa mucho en la resolución de el
determinante de 2 x 2, el método de Sarus y el
método de la estrella nos permite trabajar de una manera
muy rápida en determinantes de 3×3 y el método de
Gauss que es un proceso muy fácil y conocido nos permite
resolver determinantes de cualquier orden.

En el punto de las aplicaciones se pudo ver formas mucho
más simples que podemos usar para la resolución de
la inversa, la adjunta, en geometría analítica la
obtención del área de un triángulo, la
determinación de colinealidad de dos puntos, así
como la ecuación de la recta entre dos puntos,
etc.

Recomendaciones

Reconocer las distintas maneras de resolver una
determinante para encontrar una manera sencilla y
rápida.

Reconocer los conceptos básicos de una
determinante y aplicarlos para evitar
confusiones.

Si después de revisado todo el trabajo queda
alguna duda recomiendo revisar
la bibliografía que esta al
final.Bibliografía

• Introduccion al algebra lineal: Larson-
  Edwards

• Introduccion al algebra lineal: Howard Anton,
  tercera edición

• Algebra lineal y sus aplicaciones, David C. Lay,
  segunda edicion

• Teoria y problemas de Matrices: Frank
  Ayres

• Geometria Analitica de Lehmann

• Algebra Superior Spiegel Murray

webgrafia

•
http://descartes.cnice.mec.es/materiales_didacticos/determinantes_api/propiedades_de_los_determinantes.htm

•
http://www.virtual.unal.edu.co/cursos/ciencias/2001004/lecciones_html/cap4/cap4s2.html

•
http://www.terra.es/personal2/jpb00000/tmatrizinversa.htm

Autor:

Mateo Caldas Calle