
1 Objetivos Utilizar adecuadamente el modelo del transformador
ideal y las relaciones de corriente , voltaje y potencia que lo
caracterizan. Describir el funcionamiento de los equipos tales
como: Autotransformadores y Transformadores trifásicos.
4.4 El transformador ideal 4.5 Autotransformadores y
Transformadores Trifásicos Contenido

2 Para el circuito que se muestra en la Figura 11 deseamos
determinar todos los voltajes y corrientes especificados.
Ejemplo

3 Solución Debido a las relaciones entre los puntos, las
corrientes y voltajes, las ecuaciones del transformador son: La
impedancia reflejada en la entrada del transformador es: Por lo
tanto la corriente en la fuente es: Z1 = 16(2 + j)=32 + j16
O

4 El voltaje a través de la entrada del transformador es:
De aquí V2 es: La corriente I2 es: V1 = I1Z1 =
(2.33|-13.5º)(32 + j16) = 83.5|13.07º V Otra
técnica para simplificar el análisis de circuitos
que contienen un transformador incluye el uso del teorema de
Thévenin o de Norton para obtener un circuito equivalente
que reemplace el transformador y el circuito primario o
secundario.
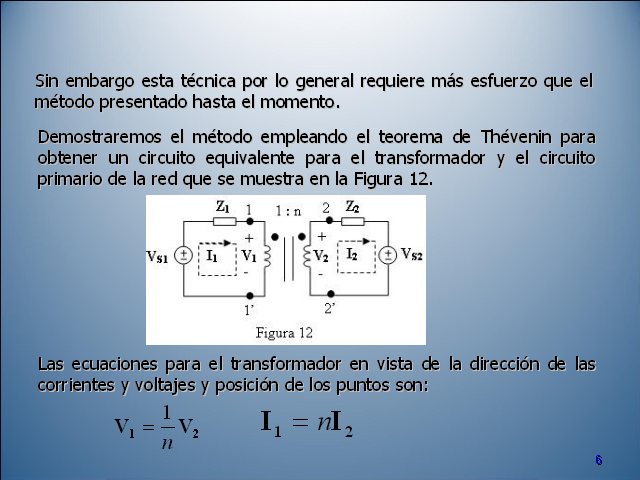
5 Sin embargo esta técnica por lo general requiere
más esfuerzo que el método presentado hasta el
momento. Las ecuaciones para el transformador en vista de la
dirección de las corrientes y voltajes y posición
de los puntos son: Demostraremos el método empleando el
teorema de Thévenin para obtener un circuito equivalente
para el transformador y el circuito primario de la red que se
muestra en la Figura 12.

6 Al formar un equivalente de Thévenin en las terminales
2-2’, como se muestra en la Figura 13, notamos que I2 = 0
y, por lo tanto I1 = 0. De aquí que: La impedancia
equivalente de Thévenin obtenida al examinar las
terminales de circuito abierto con VS1 reemplazada por un corto
circuito es Z1 que cuando se refleja en el secundario `por la
razón de vueltas es: VTH = V2= nV1= nVS1 ZTH = n2Z1 Por lo
tanto el circuito equivalente resultante puede verse en la Figura
14.

7 De manera semejante, podemos mostrar que el reemplazo del
transformador y de su circuito secundario por un circuito
equivalente de Thévenin en las terminales 1-1’, da
como resultado la red que se muestra en la Figura 15. Se puede
mostrar en general, que cuando se desarrolla un circuito
equivalente para el transformador y su circuito primario, cada
voltaje primario se multiplica por n, cada corriente primaria se
divide entre n, y cada impedancia primaria se multiplica por n2.
De manera similar, cuando se desarrolla un circuito equivalente
para el transformador y su circuito secundario, cada voltaje
secundario se divide entre n, cada corriente secundaria se
multiplica por n, y cada impedancia primaria se divide entre
n2.

8 Se debe recordar, por nuestro análisis anterior, que si
cada punto en el transformador se invierte, entonces n se
reemplaza por –n en los circuitos equivalentes. Ejemplo
Dado el circuito mostrado en la Figura 16, deseamos dibujar las
dos redes obtenidos reemplazando el transformador y el primario,
y el transformador y el secundario, con circuitos
equivalentes.

9 Solución: Debido a la relación entre corrientes y
voltajes asignados y la localización de los puntos,
podemos obtener el circuito equivalente para el secundario como
sigue: la fuente del primario al ser pasada al secundario es nVS1
= -24|0o V y la impedancia es n2Z1 = 15 – j12 O, ya que
n=2. Entonces el circuito equivalente se muestra en la Figura
17.

10 Para obtener el circuito equivalente para el primario, la
fuente del primario al ser pasada al primario es VS2/n = -24|30o
V y la impedancia es Z1/n2 = 3 + j1 O, ya que n=2. Entonces el
circuito equivalente se muestra en la Figura 18.

11 Ejemplo Determinar el voltaje de salida Vo para el circuito
mostrado en la Figura 19. Solución Comenzamos nuestro
análisis formando un equivalente de Thévenin para
el circuito primario, como es mostrado en la Figura 20.

12 El Voltaje de Thévenin y la impedancia de
Thévenin son: El circuito inicial se reduce al circuito
mostrado en la Figura 21.

13 Como la variable que buscamos esta en el secundario, entonces
pasamos el primario hacia el secundario obteniendo así el
circuito mostrado en la Figura 22. Entonces el voltaje de salida
es:

14 Los transformadores de dos devanados presentados hasta ahora
proporcionan aislamiento eléctrico entre el devanado
primario y el secundario, como se muestra en la Figura 23 (a).
Autotransformadores ideales Es posible, sin embargo,
interconectar los devanados primario y secundario en serie,
creando un dispositivo de tres terminales, como se muestra en la
Figura 23 (b).

15 Los circuitos equivalentes para la conexión aditiva y
sustractiva se muestran en la Figura 24. Este arreglo ofrece
ciertas ventajas prácticas sobre el caso aislado. Observe
que el arreglo de tres terminales es esencialmente un devanado
continuo con un punto de derivación interno (terminal Y).
Tal dispositivo comúnmente esta disponible y se llama
autotransformador. El punto de derivación puede ajustarse
para proporcionar un voltaje variable en la salida. El
autotransformador puede usarse en cualquier aplicación
práctica que requiera un transformador normal, con tal de
que no se requiera aislamiento eléctrico.

16 Es particularmente útil donde se necesita un suministro
de voltaje de salida variable (por ejemplo, en el ambiente de un
laboratorio). La Figura 25 muestra los circuitos de
conexión del autotransformador en conexión de
disminución y en conexión de
elevación.

17 Examinemos la conexión del autotransformador en
conexión de disminución que se muestra en la Figura
25. De las relaciones del transformador tenemos: Usando LVK nos
da: Entonces:

18 Sabemos que la clasificación de potencia del devanado
N1 debe ser la misma que la clasificación del devanado N2.
Sin embargo, la ecuación anterior ilustra que la
clasificación de potencia del devanado N1 (es decir, la
clasificación de potencia del transformador) es
sólo una fracción [N1/(N1+N2)] de la potencia que
es requerida por la carga. Ejemplo Un transformador de 5KVA
220V/110V se conectará para servir a una carga de 110V
desde una fuente de 330V. (a) Dibuje el diagrama apropiado del
circuito (b) Determine la carga máxima que puede ser
servida sin sobrecargar el transformador.

19 Solución (a) El diagrama apropiado del circuito se
muestra en la Figura 26, donde el devanado de 220V se asigna a N1
y el devanado de 110V se asigna a N2. (b) Como N1/N2 = 220/110,
N1 = 2N2 y Por lo tanto

20 Ejemplo Un transformador de 5KVA 220V/110V es usado para
servir a una carga de 330V desde una fuente de 220V. (a) Dibuje
el diagrama apropiado del circuito (b) Calcule todas las
corrientes si cada devanado opera a las condiciones de
clasificación (c) Calcule la potencia aparente de la
carga. Solución (a) El diagrama apropiado del circuito se
muestra en la Figura 27, donde el devanado de 220V se asigna a N1
y el devanado de 110V se asigna a N2.

21 (b) (c) S2 =V2I2 = (330)(45.45) = 15000VA, Observe que
ésta cantidad es tres veces la clasificación del
devanado. Ejemplo Para el ejemplo anterior determinemos todos los
voltajes y corrientes fasoriales si V2 = 330|0o V y si el factor
de potencia de la carga es 0.8 atrasado. Solución
Suponemos que V1 = 220|? V entonces VXY = (110/220)220|? = 110|?
V. Ahora V2 = V1 + VXY = 220|? + 110|? = 330|? V.

22 Los ejemplos han ilustrados que los transformadores de dos
devanados son capaces de entregar más potencia cuando se
conectan como autotransformador. En el transformador de dos
devanados la potencia se transfiere inductivamente, mientras que
en el autotransformador la potencia es transferida inductiva y
conductivamente. Sin embargo, como V2 = 330|?, ?=0o. Como el
factor de potencia de la carga esta atrasado, ?2 = -cos-1(0.8) =
-36.9º, y por consiguiente I2 = 45.45|-36.9º..
También IYZ=(N2/N1)I2=(110/220)(45.45)|-36.9º
=22.72|-36.9 A. Como I1=I2 + IYZ= 45.45|-36.9º + IYZ
=22.72|-36.9º= 68.18|-36.9 A. El análisis indica que
resultados similares habrían sido alcanzados para
cualquier ángulo ? o factor de potencia; es decir, V1, VXY
y V2 están en general en fase, como lo están I1, I2
e IYZ.

23 Transformadores Trifásicos Los transformadores
desempeñan un papel clave en la transmisión de
potencia trifásica de corriente alterna. Se utilizan para
elevar el voltaje de la estación generadora a la red de
transmisión de potencia de alto voltaje y para bajar el
voltaje de la red de transmisión a las cargas. La
transformación trifásica puede realizarse
utilizando un banco de transformadores de una sola fase o un
transformador trifásico. Si se usa un banco de
transformadores monofásicos, es importante asegurar que
todos los transformadores tengan características
similares, para mantener un sistema balanceado. Hay cuatro formas
posibles balanceadas en las que el transformador trifásico
puede conectarse: Y-Y, delta-delta, Y-delta, y delta-Y, como
puede ser visto en la Figura 28.

24

25

26 Los transformadores primarios con frecuencia se conectan en
delta. La razón para usar esta configuración delta
es que permite que la componente dominante de tercer
armónica, que existe típicamente en la corriente
primaria, circule en la malla primaria sin ser inducida en el
secundario. La configuración delta-delta tiene una
propiedad única. Si uno de los transformadores por alguna
razón se elimina (por ejemplo, para reparación o
mantenimiento), los otros dos transformadores, que forma ahora
una delta abierta, aún pueden proporcionar voltajes
trifásicos balanceados a una carga reducida. Cada vez que
el secundario se conecta en Y y la línea neutra se usa,
las cargas monofásicas (línea a neutro) y
trifásica (línea a línea) pueden ser
abastecidas

27 En las configuraciones Y-Y y delta-delta, las corrientes y
voltajes de línea difieren por la razón de vueltas
n. En las configuraciones Y-delta y delta-Y, entra en juego un
factor ?3. Ejemplo Una carga trifásica de 100KVA con fp de
0.8 es abastecida por un alimentador trifásico cuya
impedancia por fase es 0.01 + j0.02 O. En su extremo transmisor
el alimentador se conecta al lado de bajo voltaje de un
transformador trifásico de 12KV Y: 208V ? que suponemos es
ideal. Si el voltaje de línea en la carga es 200V, se
desea encontrar: (a) La corriente de línea en la carga (b)
El voltaje de línea en el extremo transmisor del
alimentador (c) El voltaje y corriente de línea en el lado
de alto voltaje del transformador.

28 La red se muestra en la Figura 29 Solución El voltaje
VAB = VL = 200V y por lo tanto VAN = VAB/?3= 115.5V Ya que S
=?3VLIL entonces la corriente de línea es:

29 Si ahora suponemos que VAN = 115|0o V y como el factor de
potencia es 0.8 atrasado, ? = cos-1(0.8) = 36.9º, entonces
la corriente IA’A = 288.7|-36.9 A. Entonces el voltaje de
fase en extremo transmisor del alimentador es: VA’N’
= (0.01 + j0.02)IA’A + 115.5|0o = 121.3|1.36º V
Así el voltaje de línea en el lado de bajo voltaje
del transmisor es: VL = ?3VA’N’ = 210.1 V Los
transformadores de potencia trifásica se clasifican en el
voltaje de línea, haciendo caso omiso de las conexiones Y
o delta internas. Como se supone que el transformador es ideal,
el voltaje de línea en el lado de alto voltaje del
transformador es:

30 De manera similar, la corriente de línea en el lado de
alto voltaje del transformador es: Es interesante notar que la
razón de vueltas por fase del transformador es
(12000/?3)/208. Sin embargo, el voltaje de fase en el lado de
alto voltaje del transformador es línea a neutro debido a
la conexión en Y. Por tanto, si el voltaje de línea
se determina utilizando la razón de vueltas por fase,
obtenemos: Y el factor ?3 se cancela. Consideraciones similares
afectan la corriente.