Análisis del riesgo y rendimiento de las inversiones de Chargers Products (Estudio de caso)

Caso – Capítulo 5 Análisis del Riesgo y Rendimiento
de las Inversiones de Chargers Products Junior Sayou, analista
financiero de Chargers Products, una empresa fabricante de bancas
de estadio, debe evaluar el riesgo y el rendimiento de dos
activos, X y Y. la empresa esta considerando agregar estos
activos a su cartera diversificada de activos. Para evaluar el
rendimiento y el riesgo de cada activo, Junior recolecto datos
sobre el flujo de efectivo anual y los valores de cada activo, a
principio y fin de año, durante los últimos 10
años, 1997-2006. La tabla presentada a continuación
resume estos datos. La investigación de Junior sugiere que
ambos activos tendrán, en promedio, un rendimiento futuro
similar al que tuvieron durante los últimos 10
años. Por lo tanto, cree que el rendimiento anual esperado
puede calcularse determinando el rendimiento anual promedio de
cada activo en los últimos 10 años.

Caso – Capítulo 5

Caso – Capítulo 5 Junior cree que el riesgo de cada activo
puede evaluarse de dos modos: en forma independiente y como parte
de una cartera diversificada de los activos de la empresa. El
riesgo de los activos independientes se calcula usando la
desviación estándar y el coeficiente de
variación de los rendimientos de los últimos 10
años. El modelo de precios de activos de capital (CAPM) se
utiliza para evaluar el riesgo del activo como parte de la
cartera de los activos de la empresa. Mediante algunas
técnicas cuantitativas complejas, Junior calculo los
coeficientes beta de los activos X y Y de 1.60 y 1.10
respectivamente. Además, encontró que la tasa libre
de riesgo es actualmente del 7 por ciento y que el rendimiento de
mercado es el 10 por ciento.

Caso – Capítulo 5 Calcule la tasa de rendimiento anual de
cada activo en cada uno de los 10 últimos años y
utilice estos valores para determinar el rendimiento anual
promedio de cada activo durante el periodo de 10 años.
   

Caso – Capítulo 5

Caso – Capítulo 5

Caso – Capítulo 5 b) Use los rendimientos calculados en el
inciso a para determinar: 1) la desviación estándar
y 2) el coeficiente de variación de los rendimientos de
cada activo durante al periodo de 10 años, 1997-2006. c)
Utilice los resultados que obtuvo en los incisos a y b para
evaluar y analizar el rendimiento y el riesgo relacionados con
cada activo. ¿Qué activo parece preferible?
Explique. Juzgando solamente con base a sus desviaciones
estándar la empresa preferiría el activo Y, que es
menor al activo X (2,27% contra 8,89%), igualmente el coeficiente
de variación (CV) es menor en el activo Y con respecto al
X (2,24% contra 0,75%), el CV para comparar el riesgo del activo
es efectivo, porque también considera el tamaño
relativo o rendimiento esperado de los activos por lo que Junior
Sayou debe recomendar a la empresa Chargers Products agregar el
activo Y a su cartera diversificada de activos.

Caso – Capítulo 5 d) Use el CAPM para calcular el
rendimiento requerido de cada activo. Compare este valor con los
rendimientos anuales promedio calculados en el inciso a.

Caso – Capítulo 5 Comparación: Utilizando el CAPM
(Modelo de valuación de activos de capital) se obtuvo un
11,8 % para el activo X y un 10,3% para el activo Y. Los betas
utilizados para el calculo son mayores que uno por lo que la
rentabilidad esperada de los fondos propios será mayor a
la rentabilidad del mercado, los rendimientos del activo X son
más sensibles a los cambios en los rendimientos del
mercado y, por consiguiente más riesgosos que el activo Y.
La Tasa de rendimiento promedio es una forma de expresar con base
anual, la utilidad neta que se obtiene de la inversión
promedio, el rendimiento anual promedio obtenido en el inciso a
para el activo X fue de 11,734 mientras que para el activo Y fue
de 11,139, por lo que se nota que con el activo X se obtiene mas
rendimiento.

Caso – Capítulo 5 e) Compare los resultados que obtuvo en
los incisos c y d. ¿Qué recomendaciones le
daría a Junior con respecto a invertir en alguno de los
dos activos? Explique a Junior por que le conviene mas usar el
coeficiente beta en vez de la desviación estándar y
el coeficiente de variación para evaluar el riesgo de cada
activo.   Comparando los incisos c y d, se puede notar que
en el c es preferible agregar el activo Y, mientras que
utilizando el CAPM vemos que el activo X es mas riesgoso que el
Y, por lo que se le recomendaría invertir en el activo Y,
para Junior es mas conveniente usar el coeficiente beta en vez de
la desviación estándar y el coeficiente de
variación por que es una medida relativa del riesgo no
diversificable, es un índice del grado de movimiento del
rendimiento de un activo en respuesta al cambio en el rendimiento
del mercado, el concepto de Beta de una acción o de una
cartera juega un papel importante en la determinación de
su riesgo, mientras que la desviación estándar y el
coeficiente de variación comparan el riesgo del activo
considerando el tamaño relativo, o rendimiento esperado,
de dichos activos pero no lo evalúa con respecto al
mercado, además el coeficiente beta evalúa a los
activos como parte de una cartera diversificada, mientras que el
CV y desviación estándar lo evalúan de forma
independiente.

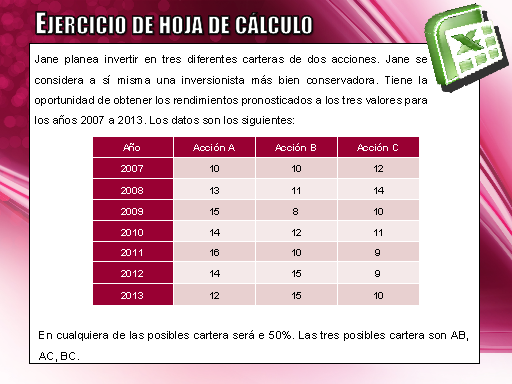
Ejercicio de hoja de cálculo Jane planea invertir en tres
diferentes carteras de dos acciones. Jane se considera a
sí misma una inversionista más bien conservadora.
Tiene la oportunidad de obtener los rendimientos pronosticados a
los tres valores para los años 2007 a 2013. Los datos son
los siguientes: En cualquiera de las posibles cartera será
e 50%. Las tres posibles cartera son AB, AC, BC.

Ejercicio de hoja de cálculo Calcule el rendimiento
esperado de cada acción individual. El rendimiento
esperado se determina calculando la media del rendimiento de cada
año

Ejercicio de hoja de cálculo Calcule la desviación
estándar de cada acción individual. Utilizando las
fórmulas de Excel (=DESVEST) se determina la
desviación estándar de los datos, es decir, el
riesgo de la inversión

Ejercicio de hoja de cálculo Calcule los rendimientos
esperados de las carteras AB, AC y BC. Para el cálculo del
rendimiento de la cartera AB, se realiza un promedio entre los
rendimiento de: La acción A Y La acción B
Obteniendo Y por último se calcula el promedio de la
columna AB

Ejercicio de hoja de cálculo Calcule las desviaciones
estándar de las carteras AB, AC y BC. Para el
cálculo de la deviación estándar de la
cartera AB, se utiliza la fórmula de Excel (=desvest) a la
columna de datos AB y así para cada cartera

Ejercicio de hoja de cálculo ¿Recomendaría
que Jane invirtiera en la acción única A o en la
cartera integrada por las acciones A y B? Explique su respuesta
desde un punto de vista de relación de riesgo y
rendimiento. La tabla siguiente muestra un resumen de la
rentabilidad y el riesgo de la acción A y la cartera AB:
La acción A tiene una rentabilidad mayor que la cartera AB
pero el riesgo se comporta de forma inversa. Por lo que se decide
realizar la siguiente recomendación: Para reducir el
riesgo de la inversión es mejor invertir en la cartera
combinada AB.

Ejercicio de hoja de cálculo ¿Recomendaría
que Jane invirtiera en la acción única B o en la
cartera integrada por las acciones B y C? Explique su respuesta
desde un punto de vista de la relación riesgo y
rendimiento. La tabla siguiente muestra un resumen de la
rentabilidad y el riesgo de la acción B y la cartera BC:
La acción B tiene una rentabilidad mayor que la cartera BC
pero el riesgo se comporta de forma inversa. Por lo que se decide
realizar la siguiente recomendación: Para reducir el
riesgo de la inversión es mejor invertir en la cartera
combinada BC.