
2 2 ? ? 2 2 2 2 2 2 SUPERFICIES CUADRÁTICAS
Introducción: La presente monografía tiene como
objetivo identificar las superficies cuadráticas y
reconocer su presencia en la naturaleza, así como mostrar
ejemplos visuales de la aplicación de éstas en
diferentes ámbitos del desarrollo humano. Debemos precisar
que no se da una definición rigurosa de superficie,
más bien intuitiva. Superficie ? Se llama superficie al
conjunto de puntos del espacio euclidiano tridimensional cuyas
coordenadas satisfacen una ecuación de la forma F ? x, y,
z ? ? 0 . Aunque la ecuación anterior expresa una
relación entre tres variables, no siempre será
así, por ejemplo: ? La ecuación y ? 2 , representa
un plano en 3 La ecuación x ? y ? 1, representa un
cilindro en 3 También debemos aclarar que la
ecuación F ? x, y, z ? ? 0 no siempre representa una
superficie. Así tenemos x ? y ? z ? 1 ? 0 que no tiene
solución en 3 Podemos decir heurísticamente que:
visto desde cerca los alrededores de un punto de una superficie
estos se parecen al plano cartesiano. O también, podemos
imaginar a una superficie como un plano deformado. ? Se llama
superficie cuadrática o cuádrica, aquella cuya
ecuación es de la forma: Ax +By +Cz
+Dxy+Exz+Fyz+Gx+Hy+Iz+J=0 Donde, al menos uno de los seis
primeros coeficientes A, B, C, D, E y F es diferente de
cero.

x2 y 2 z 2 Superficies Cuadráticas Las superficies
cuadráticas se clasifican en: ?Elipsoides. ?Paraboloides.
?Hiperboloides. ?Conos. ?Cilindros. Identificación de las
superficies cuadráticas Para identificar una
cuádrica tenemos varias opciones. Por ejemplo: Cuando los
tres coeficientes D, E y F son nulos simultáneamente, el
eje o los ejes de la superficie son paralelos a los ejes
coordenados. En estas circunstancias, los signos de los
coeficientes A, B y C permiten hacer una pre-
identificación de la superficie: Si A, B y C tienen el
mismo signo, la ecuación representará un elipsoide
cuando dichos valores sean diferentes; sin embargo si son
iguales, representará a una esfera*. Elipsoide Esfera *los
gráficos mostrados en este paper han sido creados con el
software científico MATHEMATICA 7.0 EL ELIPSOIDE: La
ecuación de un elipsoide con centro en el origen de
coordenadas y ejes coincidentes con los ejes cartesianos, es: 2 ?
2 ? 2 ? 1 , donde a ? 0, b ? 0 y c ? 0 son a b c las longitudes
de los semiejes del elipsoide respecto de los ejes x, y, z, y
determinan la forma del elipsoide. Si los tres son iguales, se
trata de una esfera. Gráficamente se tiene: Lic. Ellis R.
Hidalgo M. 2 Piura, Mayo 2013

2 2 2 1 2 Superficies Cuadráticas Ejemplo:
Clasificar y dibujar la superficie cuya ecuación
cuadrática es x ? 4 y ? 6z ? 1 . Solución: Debemos
empezar dándole forma a los coeficientes, para poner la
ecuación en la forma canónica: x 2 ? 4 y 2 ? 6 z 2
? 1 x 2 y 2 z 2 ? 1 ? 1 ? 1 4 6 La última ecuación
tiene la forma canónica de un elipsoide elíptico,
donde a ? 1, b ? 1 y c ? 16 , cuya gráfica se muestra,
observar que en la proyección sobre el plano XY, el eje
mayor de la elipse está sobre el eje X. Un vistazo al
mundo: Arquitecturas maravillosas!!! ? La forma natural de los
huevos es un elipsoide. ? La estructura arquitectónica
corresponde al Centro Nacional de las Artes Escénicas
(Pekín, China-2007), se trata en realidad de un espacio en
forma elipsoidal de 12 000 m2 con capacidad para 5 452 butacas. A
su vez el edificio está rodeado por un lago artificial.
Lic. Ellis R. Hidalgo M. 3 Piura, Mayo 2013

? ? ? ? ? ? ; 2 2 ? ? ? 0 z 2 1 2 a ? Superficies
Cuadráticas EL PARABOLOIDE ELÍPTICO: La
ecuación de un paraboloide elíptico con
vértice en el origen de coordenadas y eje sobre el eje z
tiene por ecuación: z x 2 y 2 c a 2 b2 , donde a ? 0, b ?
0 y c ? 0 Análogamente se tendrán los paraboloides:
x y 2 z 2 a b2 c2 y x 2 z 2 b a 2 c 2 Nota: Si a ? b , asume el
nombre de paraboloide circular. Ejemplo: Clasificar y dibujar la
superficie cuya ecuación cuadrática es 2x ? 4z ? y
? 0 . Solución: Debemos empezar escribiendo su
ecuación en forma canónica: 2 x2 ? 4 z 2 ? y ? 0 ?
x2 z 2 y 2 1 4 ? y 4 ? x 2 2 ? 2 La última ecuación
tiene la forma canónica de un paraboloide elíptico,
donde 2, b ? 4 y c ? 1 , observar que en la proyección
sobre el plano XZ, el eje mayor de la elipse es paralela al eje
X. Lic. Ellis R. Hidalgo M. 4 Piura, Mayo 2013
y 2 x 2 y 2 z 2 ? Superficies Cuadráticas Un
vistazo al mundo: Arquitecturas maravillosas!!! ? Las copas de
champagne nos dan una idea “digestible” de un
paraboloide. ? Las antenas parabólicas son un claro
ejemplo de la aplicación que tienen los paraboloides.
Puesto que, se demuestra que todos los rayos son reflejados hacia
el foco de la parábola generatriz. De igual modo son
usados en los faros de los automóviles, en las linternas.
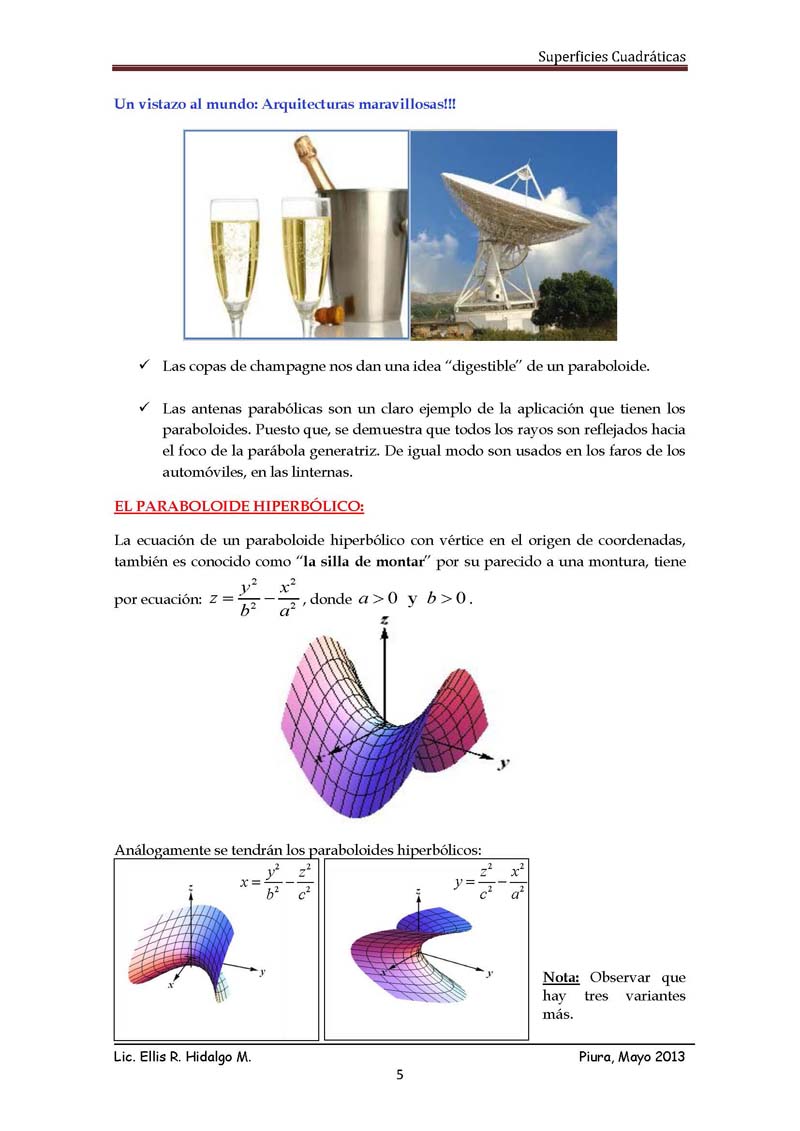
EL PARABOLOIDE HIPERBÓLICO: La ecuación de un
paraboloide hiperbólico con vértice en el origen de
coordenadas, también es conocido como “la silla de
montar” por su parecido a una montura, tiene por
ecuación: z ? 2 ? 2 , donde a ? 0 y b ? 0 . b a
Análogamente se tendrán los paraboloides
hiperbólicos: x ? 2 ? 2 b c Lic. Ellis R. Hidalgo M. 5 y ?
z 2 x2 c2 a 2 Nota: Observar que hay tres variantes más.
Piura, Mayo 2013

Superficies Cuadráticas Un vistazo al mundo:
Arquitecturas maravillosas!!! ? Algunas empresas se basan en
atractivas geometrías para registrar su marca. ? La
estructura arquitectónica corresponde al
L’Oceanographic (El oceanográfico), que se halla en
la ciudad de Ciudad de las Artes y las Ciencias (Valencia –
España 2002) donde se representa los diferentes
hábitats marinos (de mares y océanos), de
aproximadamente unos 100 000 m². HIPERBÓLOIDES: El
hiperboloide es la superficie de revolución (al igual que
el elipsoide y el paraboloide circular) generada por la
rotación de una hipérbola alrededor de uno de sus
dos ejes de simetría. Dependiendo del eje elegido, el
hiperboloide puede ser de una o dos hojas. Para entenderlo mejor,
se considera a continuación el caso de la hipérbola
y ? 1 x de referencia, si lo giramos alrededor del eje
transversal (azul), se obtiene el hiperboloide de una hoja. Pero,
si lo hacemos girar respecto al eje conjugado (rojo),
tendrá dos hojas. y x Lic. Ellis R. Hidalgo M. 6 Piura,
Mayo 2013

? ? ? ? ? ? 2 2 2 ? ? ? ? ? 1 Superficies
Cuadráticas EL HIPERBÓLOIDE DE UNA HOJA: La
ecuación de un hiperboloide de una hoja, con eje sobre el
eje z tiene por ecuación: x2 y 2 z 2 a 2 b2 c 2 ? 1 ,
donde a ? 0, b ? 0 y c ? 0 Análogamente se tendrán
los hiperboloides: x2 y 2 z 2 a 2 b2 c2 ? 1 ; ? x2 y 2 z 2 a 2 b2
c 2 ? 1 Nota: Obsérvese que el eje está definido
por la variable con coeficiente negativo. Ejemplo: Clasificar y
dibujar la superficie cuya ecuación es 2 x ? 6 y ? 4 z ?
12 ? 0 . Solución: Debemos empezar escribiendo su
ecuación en forma canónica: 2 x2 ? 6 y 2 ? 4 z 2 ?
12 ? 0 x2 y 2 z 2 6 2 3 x2 y 2 z 2 6 2 3 Lic. Ellis R. Hidalgo M.
? 1 ? 0 dividiendo entre 12 pasando ? ?1? al otro miembro Piura,
Mayo 2013 7

? ? ? ? ? ? ? ? ? ? ? ? Superficies Cuadráticas La
última ecuación tiene la forma canónica de
un hiperboloide de una hoja, donde a ? 6, b ? 2 y c ? 3 EL
HIPERBÓLOIDE DE DOS HOJAS: La ecuación de un
hiperboloide de dos hoja, con eje sobre el eje z tiene por
ecuación: x2 y 2 z 2 a 2 b2 c2 ? ?1 , donde a ? 0, b ? 0 y
c ? 0 Análogamente se tendrán los hiperboloides de
dos hojas: x2 y 2 z 2 a 2 b2 c2 ? ?1 ; x2 y 2 z 2 a 2 b2 c 2 ? 1
Ejemplo: Clasificar y dibujar la superficie cuya ecuación
cuadrática es 2×2 ? 6 y2 ? 4 z 2 ? 12 ? 0 .
Solución: Debemos empezar escribiendo su ecuación
en forma canónica: 2 x 2 ? 6 y 2 ? 4 z 2 ? 12 ? 0 x 2 y 2
z 2 6 2 3 x 2 y 2 z 2 6 2 3 y 2 x2 z 2 2 6 3 Lic. Ellis R.
Hidalgo M. ? 1 ? 0 ? ?1 ? 1 8 dividiendo entre 12 multiplicando
por ? ?1? ordenando Piura, Mayo 2013

z 2 x 2 y 2 y 2 x 2 z 2 ? ? Superficies Cuadráticas
La última ecuación tiene la forma canónica
de un hiperboloide de dos hojas, donde a ? 6, b ? 2 y c ? 3
CONOS: Son cuádricas formada por el desplazamiento de una
recta (llamada generatriz) que pasa siempre por un punto fijo
(llamado vértice) a lo largo de una curva plana (cerrada o
abierta) que se halla en una plano diferente al del
vértice, denominada directriz del cono. Pueden visitar
está dirección, para visualizar la idea:
http://www.youtube.com/watch?v=tfcL1vU8pFk CONO ELÍPTICO:
Cuando el vértice es el origen de coordenadas y la
directriz es una elipse sobre un plano paralelo al plano XY, la
superficie generada es un cono elíptico con eje sobre el
eje z tiene por ecuación: 2 ? 2 ? 2 , donde a ? 0, b ? 0 y
c ? 0 c a b Análogamente se tendrán conos: 2 ? 2 ?
2 ; b a c Lic. Ellis R. Hidalgo M. 9 x2 y 2 z 2 a 2 b2 c 2 Piura,
Mayo 2013

? ? ? ? 2 Superficies Cuadráticas Nota: Si a ? b ,
asume el nombre de cono circular. Ejemplo: Clasificar y dibujar
la superficie cuya ecuación cuadrática es x2 ? 2 y
2 ? 4 z 2 ? 0 . Solución: Debemos empezar escribiendo su
ecuación en forma canónica: x 2 ? 2 y 2 ? 4 z 2 ? 0
x 2 y 2 z 2 4 2 1 ? 0 dividiendo entre 4 y 2 x 2 z 2 2 4 1
despejando ? y ? La última ecuación tiene la forma
canónica de cono elíptico con eje sobre el eje Y,
donde a ? 2, b ? 2 y c ? 1 , observe la forma elíptica del
cono. CILINDROS: Son cuádricas formada por el
desplazamiento paralelo de una recta llamada generatriz a lo
largo de una curva plana, que puede ser cerrada o abierta,
denominada directriz del cilindro. Pueden visitar está
dirección, para visualizar la idea:
http://www.youtube.com/watch?v=15olaoynp7A Las superficies
cilíndricas son de tipos diversos, y por tanto sus
ecuaciones son variadas, entre las notables tenemos: ? Cilindro
Elíptico. ? Cilindro Parabólico ? Cilindro
Hiperbólico. Luego se muestran tan sólo tres
ejemplos de la variedad de las superficies cilíndricas que
se pueden construir. Lic. Ellis R. Hidalgo M. 10 Piura, Mayo
2013

? y a x 2 2 ? Superficies Cuadráticas CILINDRO
ELÍPTICO: Por ejemplo para la ecuación tiene la
superficie: x2 y 2 a 2 b2 ? 1, a ? 0, b ? 0 , se CILINDRO
PARABÓLICO: Por ejemplo para la ecuación tenemos la
superficie: ? , a ? 0, b ? 0 , b CILINDRO HIPERBÓLICO: Por
ejemplo para la ecuación x2 y 2 a 2 b 2 ? 1 , a ? 0, b ? 0
, tenemos la superficie: Esperamos haber cumplido con nuestro
objetivo, rogamos a los estudiantes en quienes caiga esta
monografía no dejar de maravillarse con las
matemáticas. También sugerimos el uso del empleo de
software científico para enriquecer vuestra
comprensión, por ejemplo: pueden acceder ONLINE Lic. Ellis
R. Hidalgo M. a http://www.wolframalpha.com 11 Piura, Mayo
2013

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 a Superficies
Cuadráticas Específicamente podrían acceder
a
http://www.wolframalpha.com/input/?i=quadratic+surfaces&lk=4&num=1
Para terminar, unos Ejercicios: Identificar y bosquejar la
gráfica de las siguientes superficies. 01. 4 y ? z ? x ?
16 y ? 4 z ? 20 ? 0 02. x ? y ? z ? 2 x ? 2 y ? 4 z ? 2 ? 0 03. x
? y ? z ? 4 x ? 2 y ? 2 z ? 4 ? 0 04. x ? y ? 4z 05. x ? y ? 4z
06. x ? y ? 4z 07. 16×2 ? 4 y2 ? z 2 ? 1 ? 0 08. x 2 ? y2 ? 4x ?
6 y ? z ? 9 ? 0 09. y2 ? 9z 2 ? x2 ? 9 ? 0 010. x2 ? y 2 ? 3 z 2
? 2x ? 1 ? 0 011. y ? 4 z 012. x ? 4z ? 1 Comentarios o
sugerencias: ellis.unp@facebook.com , www.facebook.com/ellis.unp
REFERENCIAS BIBLIOGRÁFICAS: 1.- RON LARSON – BRUCE
EDWARDS 2.- JAMES STEWART 3.- JERROLD MARSDEN – ANTHONY
TROMBA 4.- EDUARDO ESPINOZA RAMOS 5.- CLAUDIO PITA RUIZ Lic.
Ellis R. Hidalgo M. 12 “CÁLCULO 2”. 9na Ed.
México D.F., Mc Graw-Hill, 2010 “MULTIVARIABLE
CALCULUS” 7va Ed. USA, Cengage Learning, 2008.
“CÁLCULO VECTORIAL” 5ta Ed. Madrid,
Addison-Wesley, 2004. “GEOMETRÍA VECTORIAL EN R
” Servicios Gráficos J.J., Lima 2004
“CÁLCULO VECTORIAL” 1 Ed. MéxicoD.F.,
Prentice-Hall, 1995. Piura, Mayo 2013