Medidas de tendencia central y de posición con Excel y GeoGrebra

??¯ =
??¯ =
??¯ =
??
??
MEDIDAS DE TENDENCIA CENTRAL CON EXCEL Y GEOGEBRA

MEDIA ARITMÉTICA

MEDIA ARITMÉTICA SIMPLE
a) Para Datos sin Agrupar
La media de una población es el parámetro ?? (que se lee “miu”). Si hay N observaciones en el conjunto
de datos de la población, la media se calcula así:

??1 + ??2 + ??3 + ? + ???? ? ????
?? = =
?? ??
La media de una muestra es un estadístico ??¯ (que se lee “x barra”). Con n observaciones en el conjunto
de datos de la muestra (??1 , ??2 , … ), la media se determina así:
??¯ =
??1 + ??2 + ??3 + ? + ???? ? ????
=
?? ??
b) Para Datos Agrupados en Tablas de Frecuencias.- Cuando una serie se la agrupa en serie simple
con frecuencias para obtener la media aritmética, se multiplica la variable por la frecuencia respectiva
(f), luego se obtiene la suma de todos estos productos y luego a este valor se lo divide para el número de
elementos (n). Todo esto puede representarse mediante una fórmula matemática, así:

??1 · ??1 + ??2 · ??2 + ??3 · ??3 + ? + ???? · ???? ? ?? · ???? ? ????
= =
??1 + ??2 + ??3 +··· ???? ? ?? ??

Donde ?? = ? ?? es la frecuencia total (o sea, el número total de casos)

c) Para Datos Agrupados en Intervalos.- Cuando una serie se la agrupa en intervalos para obtener la
media aritmética, se multiplica la marca de clase de intervalo (????) por la frecuencia respectiva (??), luego
se obtiene la suma de todos estos productos y luego a este valor se lo divide para el número de elementos.
Todo esto se representa mediante la siguiente fórmula matemática:

??1 · ????1 + ??2 · ????2 + ??3 · ????3 + ? ???? · ?????? ? ?? · ?????? ? ?? · ????
= =
??1 + ??2 + ??3 +··· ???? ? ?? ??

Ejemplo ilustrativo: Calcular la media aritmética de las siguientes calificaciones de Estadística
tomadas de una muestra de 20, sin agrupar, agrupando en tablas de frecuencias y agrupando en
intervalos.
4, 8, 10, 10, 5, 10, 9, 8, 6, 8, 10, 8, 5, 7, 4, 4, 8, 8, 6 y 6

Solución:
1) Sin agrupar
? ???? 4 + 8 + 10 + 10 + 5 + 10 + 9 + 8 + 6 + 8 + 10 + 8 + 5 + 7 + 4 + 4 + 8 + 8 + 6 + 6
=
?? 20
??¯ =
144
20
= 7,2

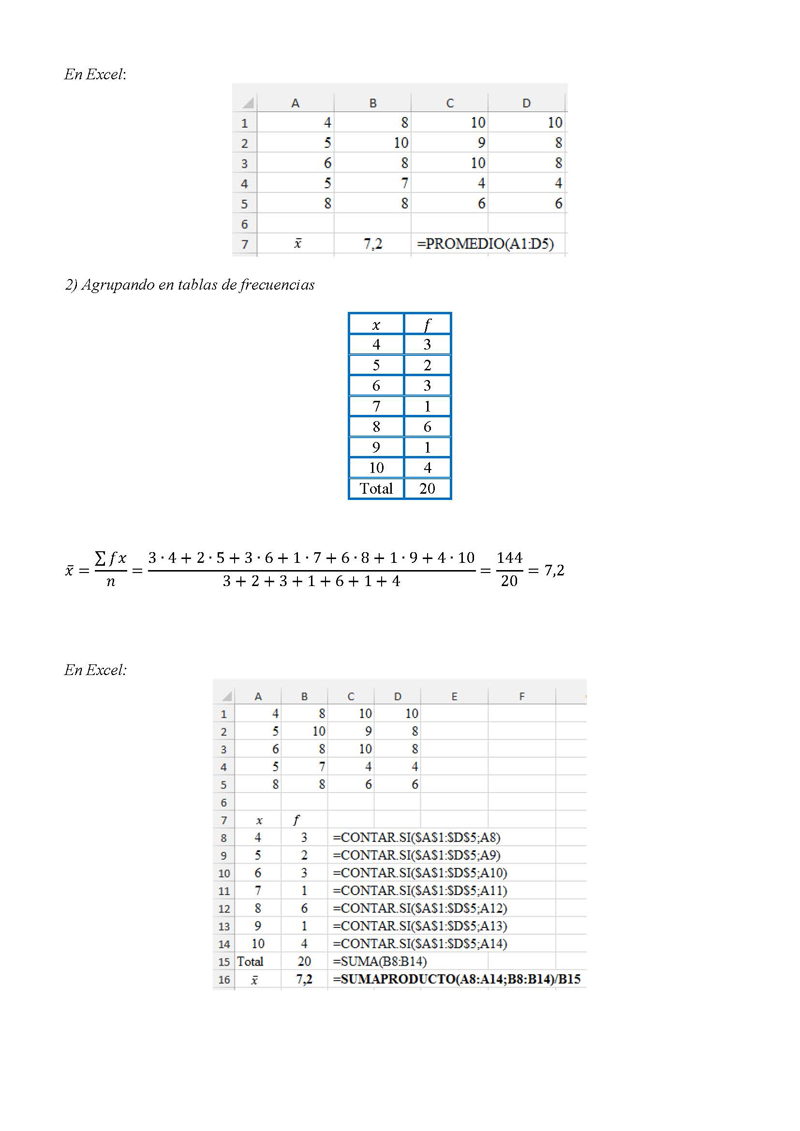
En Excel:

2) Agrupando en tablas de frecuencias
??
4
5
6
7
8
9
10
Total
??
3
2
3
1
6
1
4
20
??¯ =
? ???? 3 · 4 + 2 · 5 + 3 · 6 + 1 · 7 + 6 · 8 + 1 · 9 + 4 · 10 144
= =
?? 3+2+3+1+6+1+4 20
= 7,2
En Excel:

5
3) Agrupando en intervalos
Intervalos
4- 5
6 -7
8- 9
10-11
??
5
4
7
4
????
4,5
6,5
8,5
10,5
??¯ =
? ?? · ???? 5 · 4,5 + 4 · 6,5 + 7 · 8,5 + 4 · 10,5 150
= =
?? 5+4+7+4 20
= 7,5
Nota: Cuando se agrupa en intervalos los cálculos son sólo aproximaciones
En Excel:

Ejemplo ilustrativo de un problema:
A un estudiante le han realizado cinco evaluaciones en Matemática y su media es 7,8. Si en otras dos
evaluaciones obtiene 7 y 10, ¿cuál es el nuevo valor medio?.
Solución:
Simbolizando, “A un estudiante le han realizado cinco evaluaciones en Estadística y su media es 8”, se
obtiene:
??1 + ??2 + ??3 + ??4 + ??5
= 7,8 ? ??1 + ??2 + ??3 + ??4 + ??5 = 7,8 · 5 = 39
Simbolizando, “Si en otras dos pruebas obtiene 7 y 10, el nuevo valor medio será”, se obtiene:
??1 + ??2 + ??3 + ??4 + ??5 + 7 + 10
= ??¯
7
Remplazando ??1 + ??2 + ??3 + ??4 + ??5 = 39 en la expresión anterior se obtiene:
39 + 7 + 10 56
= ??¯ ? = ??¯ = 8
7 7

??¯ =
?? · ??
MEDIA ARITMÉTICA PONDERADA

Cuando los números ??1 , ??2 , ??3 , … ???? se les asocian ciertos factores peso (o pesos) ??1 , ??2 , ??3 , … ???? ,
dependientes de la relevancia asignada a cada número, en tal caso se requiere calcular la media aritmética
ponderada, la cual se calcula así:

??1 · ??1 + ??2 · ??2 + ??3 · ??3 + ? ???? · ???? ? ?? · ??
=
??1 + ??2 + ??3 + ? ???? ? ??

Ejemplo ilustrativo: Se tiene una información acerca de las utilidades por pan y cantidades vendidas de
panes de tres tiendas. Calcular la media aritmética promedio de la utilidad por pan.

Tienda Utilidad/pan Cantidad vendida
Solución:
1
2
3
1
0,8
0,9
2000
1800
2100
??¯ =
? ?? · ?? 2000 · 1 + 1800 · 0,8 + 2100 · 0,9 5330
= =
? ?? 2000 + 1800 + 2100 5900
= 0,90339
En Excel:

Ejemplo ilustrativo de un problema:
Una estudiante de secundaria de ecuador de la Unidad Educativa “Ibarra” obtiene en el primer quimestre,
6 en la primera parcial, 9 en la segunda parcial, 6 en la tercera parcial. Si el promedio del quimestre es
de 7,2, ¿cuál fue la calificación del examen?. Recuerde que el sistema educativo ecuatoriano secundario
las tres parciales aportan al promedio con el 80% y la nota del examen con el 20%

Solución
Evaluación Calificación(x) Ponderación(??)
1ra parcial
2da parcial
3ra parcial
examen
Total
6
9
6
??
80/3
80/3
80/3
20
100
160
240
160
20??
560 + 20??
??¯ =
? ?? · ??
? ??
= 7,2 =
560 + 20??
100
? 100 · 7,2 = 560 + 20?? ? 720 – 560 = 20?? ? 160 = 20??
?? =
160
20
? ?? = 8
MEDIA GEOMÉTRICA

??
??
a) Para Datos No Agrupados
Se emplea la ecuación:

?? = v??1 · ??2 · ??3 ··· ????

O aplicando logaritmos la ecuación:
???????? =
log ??1 + log ??2 + log ??3 + ? log ????
??
Ejemplo ilustrativo: La media geométrica es útil en el cálculo de tasas de crecimiento; por ejemplo, si
el crecimiento de las ventas en un pequeño negocio son 3%, 4%,8%,9% y 10%, hallar la media de
crecimiento.

Solución:
5
?? = v??1 · ??2 · ??3 ··· ???? = v3 · 4 · 8 · 9 · 10 = 6,128

Respuesta: 6,128%

O utilizando logaritmos:
log ??1 + log ??2 + log ??3 + ? log ???? log 3 + log 4 + log 8 + log 9 + log 10
???????? = =
?? 5
0,4771 + 0,6021 + 0,9031 + 0,9542 +1 3,9365
???????? = = = 0,7873
5 5
?? = ?????????????? 0,7873 = 6,128

En Excel:

b) Para Datos Agrupados en Tablas de Frecuencias

Se emplea la siguiente ecuación:
log ?? =
? log ???? · ????
??
Donde:
???? = ???????????????????? ???????????????? ???? ???????? ???????? ????
Ejemplo ilustrativo: Calcular la media geométrica para las siguientes calificaciones de Estadística:
Solución:
????
4
6
8
9
10
????
5
8
9
10
8

1
1
1
1
???
Se llena la siguiente tabla, realizando los cálculos respectivos:
????
4
6
8
9
10
Total
????
5
8
9
10
8
40
log ????
0,602
0,778
0,903
0,954
1,000
log ???? · ????
3,010
6,225
8,128
9,542
8,000
34,906
Se aplica la siguiente ecuación para obtener la respuesta.
log ?? =
? log ???? · ???? 34,906
=
?? 40
= 0,873
G = anti log 0,873 = 7,458

En Excel:

c) Para Datos Agrupados en Intervalos
Se emplea la ecuación:
log ?? =
? log ???? · ????
??
Donde:
xm = ?????????? ???? ??????????

MEDIA ARMÓNICA

a) Para Datos No Agrupados
Sean los números ??1 , ??2 , … ???? .La media armónica H se obtiene con la siguiente ecuación:
?? ??
?? = =
??=1 ???? ??1 + ??2 + ? ????
O con la siguiente ecuación:
?? =
1
1 1 1 1
?? (??1 + ??2 + ? ???? )
Ejemplo ilustrativo: La velocidad de producción de azúcar de tres máquinas procesadoras son 0,5, 0,3
y 0,4 minutos por kilogramo. Hallar el tiempo promedio de producción después de una jornada de 4800
minutos del proceso.

Solución:

1
???
=
???
??
??=1 ??
= =
Como en la razón minutos/kilogramos (min/kg) cada máquina trabaja 4800 min, la razón contante es el
tiempo de trabajo (4800 min), es decir la contante es la unidad del numerador, por lo tanto se debe
emplear el promedio armónico.
?? =
??

??=1 ????
=
1
??1
??
1 1
+ ??2 + ? ????
=
1
0,5
3
1 1
+ 0,3 + 0,4
= 0,383
O empleando la otra ecuación:
?? =
1 1
1 1 1 1 1 1 1 1
?? (??1 + ??2 + ? ???? ) 3 (0,5 + 0,3 + 0,4)
= 0,383
El tiempo promedio de producción es 0,383 minutos por kilogramo de azúcar.

En Excel :

b) Para Datos Agrupados en Tablas de Frecuencias
Se emplea cualquiera de las siguientes ecuaciones:
?? =
??

??=1
????
????
=
??
??1 ??2 ????
??1 + ??2 + ? ????
?? =
1
1 ??1 ??2 ????
?? (??1 + ??2 + ? ???? )
Ejemplo ilustrativo: En la siguiente tabla se presentan los datos sobre el tiempo en horas que se demoran
en realizar la misma obra determinados obreros. Calcular el tiempo promedio que se demora en realizar
la obra un obrero tipo (un obrero promedio).

Tiempo Obreros
Solución:
4
5
6
7
9
4
5
7
2
2
?? =
??
??? ??
??
=
?? 20 20
??1 ??2 ?? 4 5 7 2 2 463
??1 + ??2 + ? ???? 4 + 5 + 6 + 7 + 9 126
=
2520
463
= 5,44
En Excel:

????
???
??=1
??
????
???
??=1
c) Para Datos Agrupados en Intervalos
Se emplea la siguiente ecuación:
?? =
??

??????
=
??1
????1
??
??2 ????
+ ????2 + ? ????
Ejemplo ilustrativo: En la siguiente tabla se presentan los datos sobre el tiempo en minutos que se
demoran para resolver una prueba de Estadística determinados estudiantes. Calcular el tiempo promedio
que se demora en resolver la prueba un estudiante tipo.
Tiempo
[40-50)
[50-60)
[60-70)
[70-80)
[80-90]

Solución:
Realizando los cálculos respectivos se obtiene:
Estudiantes
4
8
10
7
11
????
[40-50)
[50-60)
[60-70)
[70-80)
[80-90]
Total
????
4
8
10
7
11
40
??????
45
55
65
75
85
???? /??????
0,089
0,145
0,154
0,093
0,129
0,611
Aplicado la ecuación se obtiene:
?? =
??

??????
=
??
??1 ??2 ????
????1 + ????2 + ? ??????
=
40
0,611
= 65,47
En Excel:

2 2
2
LA MEDIANA
La mediana, llamada algunas veces media posicional, es el valor del término medio que divide una
distribución de datos ordenados en dos partes iguales, es decir, el 50% de los datos se ubican sobre la
mediana o hacia los puntajes altos y el 50% restante hacia los puntajes bajos.
a) Para Datos No Agrupados
1) Si el número n de datos es impar, la mediana es el dato que se encuentra a la mitad de la lista. Para
calcular su posición se aplica la siguiente ecuación:
???? = ????+1 = ????+1
Ejemplo ilustrativo:
Calcular la mediana de las siguientes calificaciones del curso de Estadística evaluadas sobre diez: 10, 8,
6, 4, 9, 7, 10, 9 y 6
Solución:
Se ordena los datos de menor a mayor:
4 6 6 7 8 9 9 10 10
??1 ??2 ??3 ??4 ??5 ??6 ??7 ??8 ??9
Se aplica la ecuación:
???? = ????+1
2
???? = ??9+1 = ???? = ??5
2
La mediana es el valor de x5 (quinto dato), es decir, Md=8
En Excel :

2
2
2
2
En GeoGebra :
Escribir los datos: Mediana[ 10,8,6,4,9,7,10,6 ]. Enter

2) Si el número n de datos es par, la mediana es la media aritmética de los dos datos que se encuentran
a la mitad de la lista. Para calcular su posición se aplica la siguiente ecuación:
???? =
???? + ????+1
2
Ejemplo ilustrativo: Calcular la mediana de las siguientes calificaciones del curso de Matemática
evaluadas sobre diez: 10, 8, 9, 6, 4, 8, 9, 7, 10 y 9

Solución:
Se ordena los datos de menor a mayor:

4 6 7 8 8 9 9 9 10 10
??1 ??2 ??3 ??4 ??5 ??6 ??7 ??8 ??9 ??10
???? =
???? + ????+1
2
=
??5 + ??6 8 + 9
=
2 2
= 8,5
b) Para Datos Agrupados en Tablas de Frecuencia
Para calcular la posición de la mediana se aplica la siguiente ecuación:
???? =
?? + 1
2
Ejemplo ilustrativo:
Dados los siguientes 20 números: 1, 3, 3, 5, 5, 5, 5, 2, 2, 2, 6, 6, 4, 4, 4 ,4, 5, 5, 5, 5
Agrupar los datos en tabla de frecuencia y calcular la mediana.

Solución:

Agrupando en frecuencias
??
1
2
3
4
5
6
Total

Calculando la posición de la mediana se obtiene:
??
1
3
2
4
8
2
20
???? =
?? + 1 20 + 1
=
2 2
= 10,5
Como la posición de la mediana es 10,5, su valor es el promedio de los datos décimo y undécimo. Para
observar con claridad cuáles son los datos décimo y undécimo se aconseja calcular la frecuencia
acumulada.
??
1
2
3
4
5
6
?? ????
1 1
3 4
2 6
4 10
8 18
2 20
Total 20
Se observa que el décimo dato es 4 y el undécimo es 5, por lo tanto:
???? =
4+5
2
= 4,5
c) Para Datos Agrupados en Intervalos
??
???? = ???????? + (2
– ????
??????
) · ??
En donde:
???????? = Límite inferior del intervalo de clase de la mediana
?? = Número total de datos
???? =Frecuencia acumulada del intervalo de clase que antecede al intervalo de clase de la mediana.
?????? = Frecuencia absoluta del intervalo de clase de la mediana
?? = Ancho del intervalo
Ejemplo ilustrativo: Calcular la mediana empleando la fórmula y mediante un histograma de
frecuencias acumuladas.
Se calcula la frecuencia acumulada como se muestra en la siguiente tabla:
Intervalos
?? ????
[ 45,55)
6
6
[ 55,65) 10 16
[ 65,75) 19 35
[ 75,85) 11 46
Solución:
[ 85,95)
4 50

Se calcula la posición de la mediana de la siguiente manera:
?? 50
=
2 2
= 25
Por lo tanto el intervalo o clase de la mediana es [65,75).

Al aplicar la ecuación respectiva se obtiene:
??
???? = ???????? + (2
– ????
??????
50
) · ?? ? ???? = 65 + ( 2
– 16
19
9
) · 10 = 65 + ( ) · 10 = 65 +
19
90
19
= 69,737
Resolviendo de manera gráfica

Observando el gráfico se determina que Md = 65+AE

Los triángulos ABC y AED son semejantes, por lo que se cumple:
???? ????
=
???? ????
75 – 65 ????
=
35 – 16 25 – 16
?
10 ????
=
19 9
Despejando AE se obtiene:
10 90
· 9 = ???? ? ???? = = 4,737
19 19
Entonces, Md = 65+AE = 65+4,737= ?Md = 69,737

MEDIDAS DE POSICIÓN

[
1
2
[
]
4
4
4
4
Son similares a la mediana en que también subdividen una distribución de mediciones de acuerdo con la
proporción de frecuencias observadas. Mientas que la mediana divide a una distribución en mitades, los
cuartiles (Q) la dividen en cuartos, los deciles (D) la dividen en décimos y los puntos percentiles (P) la
dividen en centésimos.
Colectivamente, cuartiles, deciles y percentiles se denominan cuantiles. Puesto que sirven para ubicar
datos particulares dentro de ciertas porciones de una distribución de datos, toman el nombre de medidas
de posición.

CUARTILES.- Son cada uno de los 3 valores ??1 , ??2 , ??3 que dividen a la distribución de los datos en 4
partes iguales.

Primer cuartil: ??1 = ??25 , segundo cuartil: ??2 = ??5 = ??50 = Mediana, tercer cuartil: ??3 = ??75

a) Para Datos No Agrupados

La posición o ubicación de los cuartiles se encuentra aplicando la siguiente ecuación:
???? = ?? ??·??
4
+ ]
= ?? ??·??+2
4
Donde:
n = número total de datos
k = número del cuartil

Ejemplo ilustrativo: Encuentre los cuartiles dada la siguiente distribución: 6, 9, 9, 12, 12, 12, 15 y 17

Solución:
Para calcular los cuartiles se ordena los datos de menor a mayor
6 9 9 12 12 12 15 17
??1 ??2 ??3 ??4 ??5 ??6 ??7 ??8

Aplicando la ecuación para el cuartil uno se obtiene:

???? = ??[??·??+2] = ??[??+2] = ??[8+2]=??[10]=??2,5

Como la posición del cuartil 1 es 2,5, su valor es el promedio de los datos segundo y tercero
??1 = ??2,5=
??2 + ??3 9 + 9
=
2 2
=9
O también la posición 2,5 dice que el cuartil 1 está ubicado al 50% del trayecto comprendido entre el
segundo dato, que es 9 y el tercer dato que es 9, es decir, Q1= 9+0,5(9-9) = 9

Interpretación: Este resultado indica que el 25% de los datos es inferior a 9
En Excel:

En GeoGebra:

4
4
4
4
4
4
4
4
4
4
Aplicando la ecuación para el cuartil dos se obtiene:
???? = ??[??·??+2] ? ??2 = ??[??·2+2] = ??[2??+2]= ??[2·8+2]= ??[16+2]=??4,5=
??4 + ??5 12 + 12
=
2 2
= 12
O también la posición 4,5 dice que el cuartil 2 está ubicado al 50% del trayecto comprendido entre el
cuarto dato, que es 12 y el quinto dato que también es 12, es decir,
??2 = 12 + 0,5(12 – 12) = 12
Interpretación: Este resultado indica que el 50% de los datos es inferior a 12

En Excel:

En GeoGebra:
Para calcular el cuartil 2 se repite los pasos para calcular la Mediana:

Aplicando la ecuación para el cuartil tres se obtiene:
???? = ??[??·??+2] ? ??3 = ??[3??+2]=??[3·8+2]=??[24+2]=??26 = ??6,5=
??6 + ??7 12 + 15
=
2 2
= 13,5
O también la posición 6,5 dice que el cuartil 2 está ubicado al 50% del trayecto comprendido entre el
doceavo dato, que es 12 y el quinceavo dato que es 15, es decir, ??3 = 12+0,5(15-12)
??3 = 12+0,5(3)=12+1,5=13,5
Interpretación: Este resultado indica que el 75% de los datos es inferior a 13,5

En GeoGebra:

En Excel:
Repetir los pasos para el cuartil 1, y en la opción de cuartil escribir 3.
Notas importantes:
-Los cálculos en Excel para un número impar de datos coinciden con los cálculos realizados con las
ecuaciones.
-Para un número par de datos, aunque en ciertas ocasiones coinciden, suele existir diferencias en los
cálculos del Q1 y Q3 realizados con Excel. Este error de cálculo es: e = 0,25d, en donde d es la distancia
de separación de los datos
-Para el Q1 se resta el error al valor obtenido con Excel
-Para el Q3 se suma el error al valor obtenido con Excel
En nuestro ejemplo ?? = 0,25(??7 – ??6 ) = 0,25(15 – 12) = 0,25(3) = 0,75. Al sumar el error al valor
??3 inicialmente calculado con Excel se obtiene el valor correcto como se muestra en la siguiente figura:
Diagrama de caja y bigotes

Un diagrama de caja y bigotes es una representación gráfica que ayuda a visualizar una distribución de
datos: caja desde ??1 a ??3 (50% de los datos), y bigotes el recorrido (distancia desde valor mínimo hasta
el valor máximo).
De acuerdo al ejemplo ilustrativo del cálculo de cuartiles para datos sin agrupar de la distribución de
datos 6, 9, 9, 12, 12, 12, 15 y 17 se obtienen:
Valor mínimo = 6
??1 = 9; ??2 = 12; ??3 = 13,5
Valor máximo = 17
Por lo tanto el diagrama de caja y bigotes es:
El diagrama de caja y bigotes en GeoGebra se elabora de la siguiente manera:
a) Ingrese al programa.En la casilla Entrada escriba las primeras letras de DiagramaCaja
b) Seleccione DiagramaCaja[ < Offset_y>, < Escala_y>, < Lista de Datos en Bruto> ] y dicha opción
escriba DiagramaCaja[ 2,1,{6,9,9,12,12,12,15,17}]. Enter

c) Editando el diagrama de caja y bigotes se obtiene:
b) Para Datos Agrupados en Tablas de Frecuencias
Se aplica la misma ecuación empleada para el cálculo en los datos no agrupados

4
2
2
2
4
Ejemplo ilustrativo: Dada la siguiente tabla, calcular el cuartil 2:
?? ??
6 1
9 2
12 3
15 1
17 1
Solución:
1) Cálculo del cuartil 2
Aplicando la primera ecuación para el cuartil dos se obtiene:

???? = ??[??·??+2] ? ??2 = ??[??·2+2] = ??[2(??+1)]= ??[??+1]=??[8+1]= ??[9]= ??4,5
4

Como la posición del cuartil 2 es 4,5, su valor es el promedio de los datos cuarto y quinto
Para observar con claridad cuáles son los datos cuarto y quinto se aconseja calcular la frecuencia
acumulada
?? ?? ????
6 1 1
9 2 3
12 3 6
15 1 7
17 1 8

Se observa que el cuarto dato es 12 y el quinto dato es 12, por lo tanto
??2 = ??4,5=
??4 + ??5 12 + 12
=
2 2
= 12
c) Para Datos Agrupados en Intervalos
Se emplea la siguiente ecuación:
nk
Qk = LiQ + ( 4
– Fa
fQ
) · ??
Donde:
?????? = Límite inferior del intervalo de clase del cuartil
?? = Número total de datos
???? = Frecuencia acumulada del intervalo de clase que antecede al intervalo de clase del cuartil
???? = Frecuencia absoluta del intervalo de clase del cuartil
?? = Ancho del intervalo de clase del cuartil

Ejemplo ilustrativo: Dado los siguientes datos sobre pesos de un grupo de 50 personas:
Intervalos
45- 55
55- 65
65- 75
75- 85
85- 95
1) Calcular los cuartiles empleando la ecuación
??
6
10
19
11
4

-6
50
20
2) Calcular los cuartiles empleando un histograma para ??????(%) (Frecuencia relativa acumulada mediada
en porcentajes)

Solución:
1) Cálculo de los cuartiles empleando la ecuación

1.1) Cálculo del primer cuartil

Primero se calcula nk/4 y después se averigua el intervalo en el que está el cuartil, este intervalo recibe
el nombre de intervalo o clase del primer cuartil. Para averiguar el intervalo en el que están los cuartiles
se aconseja calcular la frecuencia acumulada
?? · ?? 50 · 1
=
4 4
= 12,5
Intervalos
45 – 55
55 – 65
65 – 75
75 – 85
85 – 95
n
??
6
10
19
11
4
50
????
6
16
35
46
50
Por lo tanto en este ejemplo:
El intervalo del segundo cuartil es 55-65.
El número total de datos es n =10
Se observa que 6 valores están por debajo del valor 55, es decir Fa = 6.
La frecuencia absoluta ???? del intervalo del cuartil es 10
El ancho del intervalo del cuartil es c = 65-55 =10.
Al aplicar la ecuación se obtiene:
nk
Qk = LiQ + ( 4
– Fa
fQ
50 · 1
) · c = 55 + ( 4
10
) · 10 = 55 + ( 4 ) · 10
-6
10
13
Q1 = 55 + ( ) · 10 = 55 + 6,5 = 61,5

1.2) Cálculo del segundo cuartil
Primero se calcula nk/4 y después se averigua el intervalo en el que está el cuartil, este intervalo recibe
el nombre de intervalo o clase del cuartil.
?? · 2 50 · 2
=
4 4
= 25
Por lo tanto para el segundo cuartil se tiene:
Intervalo: 65-75
n=10
Fa=16
fQ =19
c =75-65 =10

Al aplicar la ecuación se obtiene:

– 16
19
100
– 35
11
150
nk
Qk = LiQ + ( 4
– Fa
fQ
)·c
50 · 2
Q2 = 65 + ( 4
) · 10 = 65 + ( 4
– 16
19
9
) · 10 = 65 + ( ) · 10 = 65 + 4,737 = 69,937
19
1.3) Cálculo del tercer cuartil

Primero se calcula nk/4 y después se averigua el intervalo en el que está el cuartil, este intervalo recibe
el nombre de intervalo o clase del cuartil.
?? · 3 50 · 3
=
4 4
= 37,5
Por lo tanto para el segundo cuartil se tiene:
Intervalo: 75-85

?? = 10
???? = 35
???? = 11
?? = 85 – 75 = 10

Al aplicar la ecuación se obtiene:
nk
Qk = LiQ + ( 4
– Fa
fQ
)·c
50 · 3
Q3 = 75 + ( 4
) · 10 = 75 + ( 4
– 35
11
5
) · 10 = 75 + ( ) · 10 = 75 + 2,273 = 77,273
22
2) Cálculo de los cuartiles empleando un histograma para ??????(%)

2.1) Calculando la ??????(%) se obtiene:
Intervalos
45 – 55
55 – 65
65 – 75
75 – 85
85 – 95
??
6
10
19
11
4
????
6
16
35
46
50
????
0,12
0,20
0,38
0,22
0,08
?????? (%)
12
32
70
92
100
N
50
2.2) Elaborando el histograma en Excel y en Paint se obtiene la siguiente figura:

10
38
Histograma para la ??????(%)

2.3) Cálculo del primer cuartil

Observando en gráfico tenemos que el Q1 = 55 + AE

Los triángulos ABC y AED son semejantes, por lo que se cumple:
???? ????
=
???? ????
65 – 55 ????
=
32 – 12 25 – 12
?
10 ????
=
20 13
Despejando AE se obtiene:
10
20
· 13 = ???? ? ???? = 6,5
Entonces, Q1 = 55 + 6,5 = 61,5

2.3) Cálculo del segundo cuartil

Observando en gráfico tenemos que el Q2 = 65 + CI

Los triángulos CFG y CIH son semejantes, por lo que se cumple:
???? ????
=
???? ????
?
75 – 65 ????
=
70 – 32 50 – 32
?
10 ????
=
38 18
Despejando CI se obtiene:
· 18 = ???? ? ???? = 4,737

Entonces, Q2 = 65 + 4,737 = 69,737

[
+ ]
[
]
[
]
[
]
[
]= [
]= [
]=
2.3) Cálculo del tercer cuartil
Observando en gráfico tenemos que el Q3 = 75 + GM

Los triángulos GJK y GML son semejantes, por lo que se cumple:
???? ????
=
???? ????
?
85 – 75 ????
=
92 – 70 75 – 70
?
10 ????
=
22 5
Despejando CI se obtiene:
10
· 5 = ???? ? ???? = 2,273
22
Entonces, ??3 = 75 + 2,273 = 77,273

B) DECILES

a) Para Datos No Agrupados
La posición o ubicación de los deciles se encuentra aplicando la siguiente ecuación:
???? = ?? ??·?? 1 = ?? ??·??+5
10 2 10
Donde:
n = número total de datos.
k = número del decil.

Ejemplo ilustrativo:Calcular el quinto decil de la siguiente distribución: 6, 9, 9, 12, 12, 12, 15 y 17

Solución: Para calcular los deciles se ordena los datos de menor a mayor.
6 9 9 12 12 12 15 17
??1 ??2 ??3 ??4 ??5 ??6 ??7 ??8

Aplicando la ecuación para el quinto decil se obtiene:
???? = ?? ??·??+5
10
??5 = ?? ??·5+5 = ?? 5??+5 ?? 5·8+10 ?? 40+5 ??4,5=
10 10 10 10
??4 + ??5 12 + 12
=
2 2
= 12
O también la posición 4,5 dice que el decil 5 está ubicado al 50% del trayecto comprendido entre el
cuarto dato, que es 12 y el quinto dato que también es 12, es decir,
D5= 12+0,5(12-12) = 12

En Excel:
Como D5 es igual a P50 :

[
+ ]
[
]
[
]= [
]= [
]=
[
]
b) Para Datos Agrupados en Tablas de Frecuencia
Se emplea la misma ecuación utilizada en el cálculo de los deciles para datos sin agrupar.

c) Para Datos Agrupados en Intervalos
Se emplea la siguiente ecuación:
nk
Dk = LiD + (10
– Fa
fD
) · ??
Donde:
?????? = Límite inferior del intervalo de clase del decil.
?? = número total de datos.
???? = Frecuencia acumulada del intervalo de clase que antecede al intervalo de clase del decil.
???? = Frecuencia absoluta del intervalo de clase del decil.
?? = Ancho del intervalo de clase del decil.

C) PERCENTILES O CENTILES
a) Para Datos No Agrupados
La posición o ubicación de los percentiles se encuentra aplicando la siguiente ecuación:
???? = ?? ??·?? 1 = ?? ??·??+50
100 2 100
Donde:
n = número total de datos
k = número del percentil
Ejemplo ilustrativo: Calcular los percentiles de orden 20 y 33 del peso de diez personas que pesan
(en kg)
80, 78, 65, 73, 65, 67, 72, 68, 70 y 72
Solución:
Se ordena los datos de menor a mayor se tiene:

65 65 67 68 70 72 72 73 78 80
??1 ??2 ??3 ??4 ??5 ??6 ??7 ??8 ??9 ??10
1) Cálculo del percentil de orden 20 se obtiene:
???? = ?? ??·??+50 = ?? ??·20+50 ?? 10·20+50 ?? 250 ??2,5=
100 100 100 100
??2 + ??3 65 + 67
=
2 2
= 66
En Excel se obtiene un valor aproximado insertando la función PERCENTIL.INC(A1:A10:0,2) como se
muestra en la siguiente figura:

100
100
100
100
2) Cálculo del percentil de orden 33 se obtiene:
???? = ??[??·??+50] = ??[??·33+50]=??[10·33+50]=??[380]=??3,8=
??3 + ??4 67 + 68
=
2 2
= 67,5 = 68
En Excel:

b) Para Datos Agrupados en Tablas de Frecuencia
Se emplea la misma ecuación utilizada en el cálculo de los percentiles para datos sin agrupar.

c) Para Datos Agrupados en Intervalos
Se emplea la ecuación:

nk
Pk = LiP + (100 – Fa) · c
fP

Donde:
?????? =Límite inferior del intervalo de clase del percentil.
?? = número total de datos.
???? = Frecuencia acumulada del intervalo de clase que antecede al intervalo de clase del percentil.
???? = Frecuencia absoluta del intervalo de clase del percentil.
?? = Ancho del intervalo de clase del percentil.

MODA

a) Para Datos No Agrupados
Se observa el dato que tiene mayor frecuencia

Ejemplo ilustrativo N° 1: Determinar la moda del conjunto de datos 2, 4, 6, 8, 8 y 10

Solución: Mo = 8, porque es el dato que ocurre con mayor frecuencia. A este conjunto de datos se le
llama unimodal

En Excel:
Ejemplo ilustrativo N° 2: Determinar la moda del conjunto de datos: 2, 4, 6, 8 y 10
Solución: Este conjunto de datos no tiene moda, porque todos los datos tienen la misma frecuencia.
Ejemplo ilustrativo N° 3: Determinar la moda del conjunto de datos: 8, 4, 6, 6, 8, 2 y 10
Solución: Este conjunto de datos tiene dos modas, 8 y 6, y se llama bimodal.
En Excel:
Se inserta la función MODA.VARIOS, la cual debe especificarse como fórmula de matriz, para lo cual
se selecciona las celdas donde aparecerá la respuesta (B9:B10). Luego se inserta la función MODA
.VARIOS, se selecciona las celdas respectivas (A1:A7). Finalmente, se presiona Ctrl+Blog
Mayús+Enter.
b) Para Datos Agrupados en Tablas de Frecuencia
Se observa el dato tiene mayor frecuencia
Ejemplo ilustrativo: Calcule la moda o modas (si las hay) de los siguientes datos:
?? f
2 1
4 2
6 3
8 1
10 1
Solución:
Se observa que el dato con mayor frecuencia es 6, por lo tanto Mo = 6

???? + ????
80
11
c) Para Datos Agrupados en Intervalos
Se halla en el intervalo o clase que tenga la frecuencia más alta, llamada intervalo o clase modal. Se
emplea la siguiente ecuación:
???? = ?????? + (
????
???? + ????
) · ??
????0= Límite inferior de la clase modal.
???? = Diferencia entre la frecuencia absoluta de la clase modal y la clase que la antecede.
???? = Diferencia entre la frecuencia absoluta de la clase modal y la clase que le sigue.
?? = ancho de la clase modal.

Ejemplo ilustrativo: Calcule la moda o modas (si las hay) de los siguientes datos:

Intervalo o Clase ??
10-19
20-29
30-39
40-49
50-59
3
7
15
12
8
Solución: Se observa que la clase modal es 30-39, ya que es el intervalo con la mayor frecuencia.
Aplicando la ecuación
???? = ?????? + (
Se tiene:
????
) · ??
15 – 7
???? = 30 + (
(15 – 7) + (15 – 12)
8
) · 10 = 30 + ( ) · 10 = 30 +
8+3
= 37,27
Gráficamente empleando un histograma se calcula la moda de la siguiente manera:

La clase modal es 30-39, ya que es el intervalo con la mayor frecuencia
Observando el histograma se tiene que Mo = 30 + FB
Los triángulos ABC y EBD son semejantes, por lo que se cumple:

???? ????
=
???? ????
Donde:

AC = Diferencia entre la frecuencia absoluta de la clase modal y la clase que la antecede.
BG es igual al ancho del intervalo 30-39 menos FB.
DE = Diferencia entre la frecuencia absoluta de la clase modal y la clase que le sigue.

Remplazando valores y despejando FB se tiene:
???? 10 – ???? ???? 10 – ????
= ? = ? 3???? = 8(10 – ????) ? 3???? = 80 – 8????
15 – 7 15 – 12 8 3
80
3???? + 8???? = 80 ? 11???? = 80 ? ???? = = 7,27
11
Por lo tanto Mo = 30 + FB = 30+7,27 = 37,27
Fuente:
Suárez, Mario. & Tapia, Fausto. (2014). Interaprendizaje de Estadística Básica. Ibarra, Ecuador:
Universidad Técnica de Norte
Suárez, Mario. (2014). Probabilidades y Estadística empleando las TIC. Ibarra, Ecuador: Imprenta
GRAFICOLOR
Libros y artículos del Mgs. Mario Suárez sobre Aritmética, Álgebra, Geometría, Trigonometría, Lógica
Matemática, Probabilidades, Estadística Descriptiva, Estadística Inferencial, Cálculo Diferencial, Cálculo
Integral, y Planificaciones Didácticas se encuentran publicados en:
http://es.scribd.com/mariosuarezibujes
http://repositorio.utn.edu.ec/handle/123456789/760
http://www.docentesinnovadores.net/Usuarios/Ver/29591