Vectors and the geometry of space

Enviado por Efrain Olivo

Partes: 1, 2

Monografias.com

C H A P T E R 1 1
Vectors and the Geometry of Space
Section 11.1

Section 11.2

Section 11.3

Section 11.4

Section 11.5

Section 11.6

Section 11.7
Vectors in the Plane……………………………………………………………………..2

Space Coordinates and Vectors in Space ……………………………………..13

The Dot Product of Two Vectors…………………………………………………22

The Cross Product of Two Vectors in Space ………………………………..30

Lines and Planes in Space …………………………………………………………..37

Surfaces in Space……………………………………………………………………….50

Cylindrical and Spherical Coordinates …………………………………………57
Review Exercises …………………………………………………………………………………………….68

Problem Solving ……………………………………………………………………………………………..76

Monografias.com

y
3
y
y
3
2
C H A P T E R 1 1
Vectors and the Geometry of Space

Section 11.1 Vectors in the Plane
1. (a) v
(b)
5 1, 4 2
4, 2
7. u
v
6 0, 2 3
9 3, 5 10
6, 5
6, 5
5
4
u
v
(4, 2)
8. u
11 4 , 4 1
15, 3
2
1
v
x
v
u
25 0, 10 13
v
15, 3
1
2
3
4
5
9. (b) v
5 2, 5 0
3, 5
2. (a) v
(b)
3 3, 2 4
y
0, 6
(c) v
(a), (d)
3i 5j
y
-3 -2 -1
-1
1
2
3
x
5
4
(3, 5)
(5, 5)
-2
-3
v
3
2
v
-4
-5
1
(2, 0)
x
-6
(0, – 6)
-1
-1
1
2
3
4
5
3. (a) v
4 2, 3 3
6, 0
10. (b) v
3 4, 6 6
1, 12
(b)
4
(c) v
(a), (d)
i 12 j
y
(-1, 12)
-8
(-6, 0)
-6
-4
v
-2
2
x
v
8
6
(3, 6)
-2
4
2
-4
-8 – 6 – 4 -2
2
6 8 10
x
– 4
4. (a) v
1 2, 3 1
3, 2
– 6
(4, -6)
(b)
11. (b) v
(c) v
6 8, 1 3
2i 4 j
2, 4
(- 3, 2)
2
(a), (d)
y
6
v
1
4
2
(8, 3)
v
-3
-2
-1
x
-4 -2
2
4
(6, – 1)
8
x
5. u
v
u

6. u
v
u
5 3, 6 2
3 1, 8 4
v

1 4 , 8 0
7 2, 7 1
v
2, 4
2, 4

5, 8
5, 8
(-2, -4)
-6
© 2010 Brooks/Cole, Cengage Learning

Monografias.com

3
6
y
y
3
6
6
2
2 2
2
7
2
v
3
3
5
y
3
2
3
y
2
3
2 3
y
Section 11.1
Vectors in the Plane
12. (b) v
5 0, 1 4
5, 3
17. (a) 2 v
2 3, 5
6, 10
(c) v 5i 3j
(a) and (d).
(- 5, 3)
4
y
10
8
6
y
(3, 5)
(6, 10)
v
2
4
v
2v
2
x
-6 -4
(- 5, -1)
-2
-2
2
-2
-2
2
4
6
8
10
x
(0, – 4)
(b) 3v
9, 15
13. (b) v
6 6, 6 2
0, 4
(3, 5)
(c) v
4 j
3
v
x
(a) and (d).
(6, 6)
-15 -12 -9 -6 -3
-3v -6
-9
(-9, – 15)
-12
4
(0, 4)
v
-15
2
(6, 2)
(c)
7 v
21, 35
x
y
2
4
6
18
(21, 35 (
14. (b) v
(c) v
3 7, 1 1
10i
10, 0
15
12
9
6
(3, 5)
(a) and (d).
y
3
v
x
3
-3
-3
3
6
9
12 15 18
2
(-10, 0)
v
1
x
(d)
2 v
2, 10
-8 -6 -4 -2
(-3, -1)
-2
-3
2 4 6 8
(7, -1)
4
(3, 5)
3
v
(2, 10 (
15. (b) v
1
2
3 , 3
4
3
1, 5
2
1
2
3
v
(c) v
i
5
3
j
-1
-1
1
2
3
4
5
x
(a) and (d)
3
( 1 , 3(
(- 1, 5 ( 2
v

( 3 , 4 (
– 2
-1
1
2
x
16. (b) v
(c) v
0.84 0.12, 1.25 0.60
0.72i 0.65 j
0.72, 0.65
(a) and (d).
1.25
1.00
0.75
0.50
0.25
(0.12, 0.60)
(0.84, 1.25)

(0.72, 0.65)

v
x
0.25 0.50 0.75 1.00 1.25
© 2010 Brooks/Cole, Cengage Learning

Monografias.com

4
y
u
2
2
2
3
3
2
y
3
3
3
v
1
1
x
2
y
2
y
-1
Chapter 11
Vectors and the Geometry of Space
18. (a) 4 v
4 2, 3
8, 12
21.
y
(- 8, 12) 12
10
4v
8
6
4
u – v
– v
x
(-2, 3)
v
x
-8 – 6 – 4 -2

(b) 1 v
2

1, 3
4
6
22.
y
u + 2v
y
(-2, 3)
3
2
2v
v
x
u
x
-3 -2 -1
– 1 v
3
-2
-3
(1, – 3(
23. (a)
2 u
2
3
4, 9
8 , 6
(b) v u
2, 5 4, 9
2, 14
(c) 0 v
0, 0
(c) 2u 5v
2 4, 9 5 2, 5
18, 7
(-2, 3)
24. (a)
2 u
2
3
3, 8
2, 16
2
(b) v u
8, 25 3, 8
11, 33
-3
-2
-1
0v
(c) 2u 5v
2 3, 8 5 8, 25
34, 109
-1
(d) 6u
12, 18
25. v
3
2
2i
j
3i
3 j
3, 3
y
(- 2, 3)
1
-6
v
-2
2
6
10
14
x
2
3
x
-6
-10
-14
– 6v
-1

-2
3
2
u
u
-18
(12, -18)
-3
19.
26. v
2i
j i 2 j
3i j
3, 1
y
– u
2
x
1
w
v
x
1
2
3
u
20. Twice as long as given vector u.
y

u
2u

Monografias.com

5
y
4
§ 3 · § 5 ·
©
2 ¹
© 2 ¹
v
2
© 2 ¹ © 2 ¹
v
2
2
2
2
Section 11.1
Vectors in the Plane
27. v
2i
j 2 i 2 j
4i 3j
4, 3
38. v
5, 15
v
25 225
250
5 10
2w
u
v
v
5, 15
5 10

10 3 10
,
10 10
unit vector
2
u + 2w
u
4
6
x
39. v
3 5
,
2 2
-2

28. v
5u 3w
5 2, 1 3 1, 2
7, 11
2
¨ ¸ ¨ ¸
34
2
-4 -2
2
y
4
6
8
10
x
u
v
v
§ 3 · § 5 ·
¨ ¸, ¨ ¸
34
3
34
,
5
34
-3w
5u
2
-6
-8
-10
-12
40. v
6.2, 3.4
3 34 5 34
,
34 34
unit vector
29. u1 4
u2 2
1
3
u1
u2
Q
3
5
3, 5
v

u
v
v
6.2 3.4
6.2, 3.4
5 2

50 5 2

31 2 17 2
,
50 50
unit vector
30. u1 5
u2 3
4
9
u1
u2
9
6
41. u
1, 1 , v
1, 2
Q
9, 6
Terminal point
(a)
u
1 1
2
31.
v
0 72
7
(b)
v
1 4
5
(c)
u v
0, 1
32.
v
3
2
0
3
u v
0 1
1
33.

34.
v

v
42 32

122 5
2
5
13
(d)
u
u

u
u
1
1
2
1, 1
35.
v
62 5
2
61
(e)
v
v
1
5
1, 2
36.
v
10 2
32
109
v
v
1
37. v

v
3, 12

3 12
153
(f )
u v
u v
0, 1
u
v
v
3, 12
153
3
153
,
12
153
u v
u v
1
17 4 17
,
17 17
unit vector
© 2010 Brooks/Cole, Cengage Learning

Monografias.com

6
1
x
6¨
6 0, 1
©
¹
Chapter 11
Vectors and the Geometry of Space
42. u
0, 1 , v
3, 3
44. u
2, 4 , v
5, 5
(a)

(b)

v
u v
0 1
9 9
3, 2
1

3 2
(a)

(b)

v
u v
4 16
25 25
7, 1
2 5

5 2
u v
9 4
13
u v
49 1
5 2
(d)
u
u
0, 1
(d)
u
u
1
2 5
2, 4
u
u
1
u
u
1
(e)
v
v
1
3 2
3, 3
(e)
v
v
1
5 2
5, 5
v
v
1
v
v
1
(f )
u v
u v
1
13
3, 2
(f )
u v
u v
1
5 2
7, 1
u v
u v
1
u v
u v
1
43. u
1,
1
2
, v
2, 3
45.
u
u
2, 1
5 | 2.236
7
y
(a)

(b)
u

v
1
4
4 9
5
2
13
v
v
u v
5, 4
41 | 6.403
7, 5
6
5
4
3
2
1
v
u
u + v
(c)
u v

u v
7
3,
2

9
49
4
85
2
u v 74 | 8.602
u v d u v
74 d 5 41
-1
1
2
3
4
5
6
7
(d)

(e)
u
u

u
u

v
v

v
v
1

1
2
5

1
13
1
1,
2

2, 3
46.
u 3, 2
u 13 | 3.606
v 1, 2
v 5 | 2.236
u v 2, 0
u v 2
u+ v d u v
u

u+v
-3 -2 -1
3
2
1

-1
-2
-3
y
1
v
2
3
x
(f )
u v
u v
u v
u v
1
2
85
3,
7
2
47.
2 d 13

u 1
0, 3 0, 1
u 3
§ u ·
¨ u ¸
5

0, 6
v
0, 6
© 2010 Brooks/Cole, Cengage Learning

Monografias.com

7
4¨
©
¹
¬ ¼ ¬ ¼
5¨
©
¹
1
S
,
,
2¨
©
¹
3i
52. v
¬ ¼
¬ ¼
5
,
j
a
¬ ¼
¬ ¼
u
v
j
¸i
¨
©
¹
,
j
u
3
3
v
u
v
Section 11.1
Vectors in the Plane
48.
u
u
§ u ·
¨ u ¸
1
1, 1
2

2 2 1, 1
58.
u

v
u v
5ªcos 0.5 º i 5ªsin 0.5 º j
5 cos 0.5 i 5 sin 0.5 j
5 cos 0.5 i 5 sin 0.5 j
10 cos 0.5 i 10 cos 0.5, 0
v
2 2, 2 2
59. Answers will vary. Sample answer: A scalar is a real
49.
u
u
§ u ·
¨ u ¸
1
5
1, 2

5
5

2
5
1
5
2
5

5, 2 5
number such as 2. A vector is represented by a directed
line segment. A vector has both magnitude and direction.
For example 3, 1 has direction and a magnitude
6
of 2.
v

5, 2 5
60. See page 766:
(ku1, ku2)
50.
u
u
1
2 3
3, 3
(u1, u2)
(u1 + v1, u2 + v2)
u + v
ku
ku2
§ u ·
¨ u ¸
1
3
3, 3
u
(v1, v2)
v
u2

v2
u1
u
(u1, u2)
u2
v
1,
3
v1
u1
ku1
51. v
3ª cos 0q i sin 0q jº

5ª cos 120q i sin 120q jº
3, 0
61. (a) Vector. The velocity has both magnitude and
direction.
(b) Scalar. The price is a number.
i
2
5 3
2
5 5 3
2 2
62. (a) Scalar. The temperature is a number.
(b) Vector. The weight has magnitude and direction.
53. v
2ª cos 150q i sin 150q jº
3i j 3, 1
For Exercises 63–68,
au bw a i 2j b i j
b i 2a b j.
54. v
4ª cos 3.5q i sin 3.5q jº
63. v 2i j. So, a b 2, 2a b
simultaneously, you have a 1, b
1. Solving
1.
| 3.9925i 0.2442 j
3.9925, 0.2442
64. v
3j. So, a b
0, 2a b
3. Solving
simultaneously, you have a
1, b
1.
55.
cos 0q i sin 0q j i
3 cos 45q i 3 sin 45q j
3 2
2
i
3 2
2
65. v 3i. So, a b 3, 2a b
simultaneously, you have a 1, b
0. Solving
2.
u v
§ 2 3 2 ·
¨ 2 ¸
3 2
2
2 3 2 3 2
2 2
66. v 3i 3j. So, a b
simultaneously, you have a
3, 2a b
2, b
1.
3. Solving
56.
4 cos 0q i 4 sin 0q j
4i
67. v
i j. So, a b
1, 2a b
1. Solving
2 cos 30q i 2 sin 30q j
i
3j
simultaneously, you have a
2 , b
1 .
u v
5i
3j
5,
3
68. v
i 7 j. So, a b
1, 2a b
7. Solving
57.
2 cos 4 i 2 sin 4 j
simultaneously, you have a
2, b
3.
cos 2 i sin 2 j
u v
2 cos 4 cos 2 i 2 sin 4 sin 2 j
2 cos 4 cos 2, 2 sin 4 sin 2
© 2010 Brooks/Cole, Cengage Learning

Monografias.com

8
6
y
8
6
x
6
y
4
3
y
2
1
1
y
4
x
y
3
1
2
1
y
2
4
x
1
Chapter 11
Vectors and the Geometry of Space
69. f x
x 2 , f c x
2 x, f c 3
10
(a) m
6. Let w
1, 6 , w
37, then r
w
w
r
1
37
1, 6 .
(a)
4
(b)
(b) m
1 . Let w
6, 1 , w
37, then r
w
w
r
1
37
6, 1 .
-2
2
2
(3, 9)
4
6
8
10
70. f x
x 2 5, f c x
2 x, f c 1
2
(a) m
2. Let w
1, 2 , w
5, then r
w
w
r
1
5
1, 2 .
(a)

(1, 4)
(b)
(b) m
1
2
. Let w
2, 1 , w
5, then r
w
w
r
1
5
2, 1 .
-3
-1
2
1

-1
1
2
3
x
71. f x
x3 , f c x
3x 2
3 at x
1.
(a) m
3. Let w
1, 3 , w
10, then
w
w
r
1
10
1, 3 .
(a)
(b) m
. Let w
3
3, 1 , w
10, then
w
w
r
1
10
3, 1 .
(1, 1)
(b)
x
1
2
72. f x
x3 , f c x
3x 2
12 at x
2.
(a) m
12. Let w
1, 12 , w
145, then
w
w
r
1
145
1, 12 .
-6
-4
-2
-4
2
(a)
(b) m

1
12
. Let w
12, 1 , w
145, then
w
w
r
1
145
12, 1 .
-6
(b)
-10
73. f x
25 x 2
f c x
x
25 x 2
3
4
at x
3.
4
3
(a)
(3, 4)
(b)
(a) m
. Let w
4
4, 3 , w
5, then
w
w
r 4, 3 .
5
(b) m
4
3
. Let w
3, 4 , w
5, then
w
w
r
1
5
3, 4 .
-1
1
2
3
4
5
x
74. f x
tan x
f c x
sec2 x
2 at x
S
4
2.0
1.5
(a)
(a) m
2. Let w
1, 2 , w
5, then
w
w
r
1
5
1, 2 .
– p
– p
1.0
0.5
p
4
(b)

p
2
(b) m
. Let w
2
2, 1 , w
5, then
w
w
r
1
5
2, 1 .
-1.0
© 2010 Brooks/Cole, Cengage Learning

Monografias.com

9
2
j
y
1
2
6
x
R
R
81.
2
2
§ 90 ·
© 430.88 ¹
2
arctan « »
D
Section 11.1
Vectors in the Plane
75.
u

u v
i
2
2 j
2
2
78. (a) v
(b) v
(c)
9 3, 1 4
6i 5 j
6, 5
v
u v u

2
2
i
2
2
j

2
2
,
2
2
6
5
4
(6, 5)
3
v
76.
u
2 3i 2 j
2
1
u v
v
3i 3 3j
u v u
3 2 3 i 3
3 2 j
(d)
-1

v
3 4 5

62 52
61
3 2 3, 3 3 2

77. (a)–(c) Programs will vary.
(d) Magnitude | 63.5
79.
F1
F2
F3
2, TF1
3, TF2
2.5, TF3
33q
125q
110q
Direction | 8.26q
T R
F1 F2 F3 | 1.33
TF1 F2 F3 | 132.5q
80.
F1
F2
F3
2, TF1
4, TF2
3, TF3
10q
140q
200q
F1 F2 F3 | 4.09
T R
TF1 F2 F3 | 163.0q
F1 F2
500 cos 30qi 500 sin 30q j 200 cos 45q i 200 sin 45q j
250
3 100 2 i 250 100 2 j
F1 F2
250
3 100 2
250 100 2
| 584.6 lb
tan T
250 100 2
250 3 100 2
? T | 10.7q
82. (a) 180 cos 30qi sin 30q j 275i | 430.88i 90 j
Direction: D | arctan¨ ¸ | 0.206 | 11.8q
Magnitude:
430.882 902 | 440.18 newtons
(b) M
275 180 cos T 2
180 sin T
ª 180 sin T º
¬ 275 180 cos T ¼
(c)
T
M
D
0q
455
0q
30q
440.2
11.8q
60q
396.9
23.1q
90q
328.7
33.2q
120q
241.9
40.1q
150q
149.3
37.1q
180q
95
0
(d)
500
M
50
a
0
0
180
0
0
180
(e) M decreases because the forces change from acting in the same direction to acting in the opposite direction as T increases
from 0q to 180q.

Monografias.com

10
125
125
75 3 50 2 i 75 50 2
2
2
2
2
R
¬
¼
¬
¼
¬ ¼ ¬ ¼ ¬ ¼
2
R
2
arctan¨
T R
q.
© ¹
S .
3
P
1
P2
Chapter 11

83. F1 F2 F3

T R

84. F1 F2 F3
Vectors and the Geometry of Space

75 cos 30qi 75 sin 30q j 100 cos 45qi 100 sin 45q j 125 cos 120qi 125 sin 120q j
3 j
F1 F2 F3 | 228.5 lb
TF1 F2 F3 | 71.3q
ª400 cos 30q i sin 30q j º ª280 cos 45q i sin 45q j º ª350 cos 135q i sin 135q j º
ª200 3 140 2 175 2 ºi ª 200 140 2 175 2 º j
200
3 35 2
200 315 2
| 385.2483 newtons
§ 200 315 2 ·
¨ 200 3 35 2 ¸ | 0.6908 | 39.6q

85. (a) The forces act along the same direction. T
(b) The forces cancel out each other. T
180q.
(c) No, the magnitude of the resultant can not be greater than the sum.
86. F1

(a)
20, 0 , F2
F1 F2
10 cos T sin T
20 10 cos T , 10 sin T
400 400 cos T 100 cos2 T 100 sin 2 T
500 400 cos T
(b)
0
40
2
0
(c) The range is 10 d F1 F2 d 30.
The maximum is 30, which occur at T
The minimum is 10 at T
(d) The minimum of the resultant is 10.
87. 4, 1 , 6, 5 , 10, 3
0 and T
2S .
8
y
8
y
8
y
6
4
(1, 2)
(8, 4)
6
4
(1, 2)
(6, 5)
(8, 4)
6
4
(1, 2)
(8, 4)
2

(- 4, -1)
2
4
(3, 1)
6
8
x
2
-4 -2
-2
2
4
(3, 1)
6
8
x
2
-2
-2
(3, 1)
4
6
8
(10, 3)
x
10
-4
-4
-4
88.
u
1 u
7 1, 5 2
2, 1
6, 3
1, 2 2, 1 3, 3
1, 2 2 2, 1 5, 4

Monografias.com

11
CB
CA
JJJ
JJJ
G
G
y
A
u
v
0
u ¨
©
¹
100.
0 or
§ 24 ·
T2
§ 24 ·
© 10 ¹
u
v
§ 1 ·
0.
© 2 ¹
3 and adding to the
§ 1 ·
0 gives
© 2 ¹
5000
0
v
v
u v
§ 547.64 ·
© 692.53 ¹
2
2
Section 11.1
Vectors in the Plane
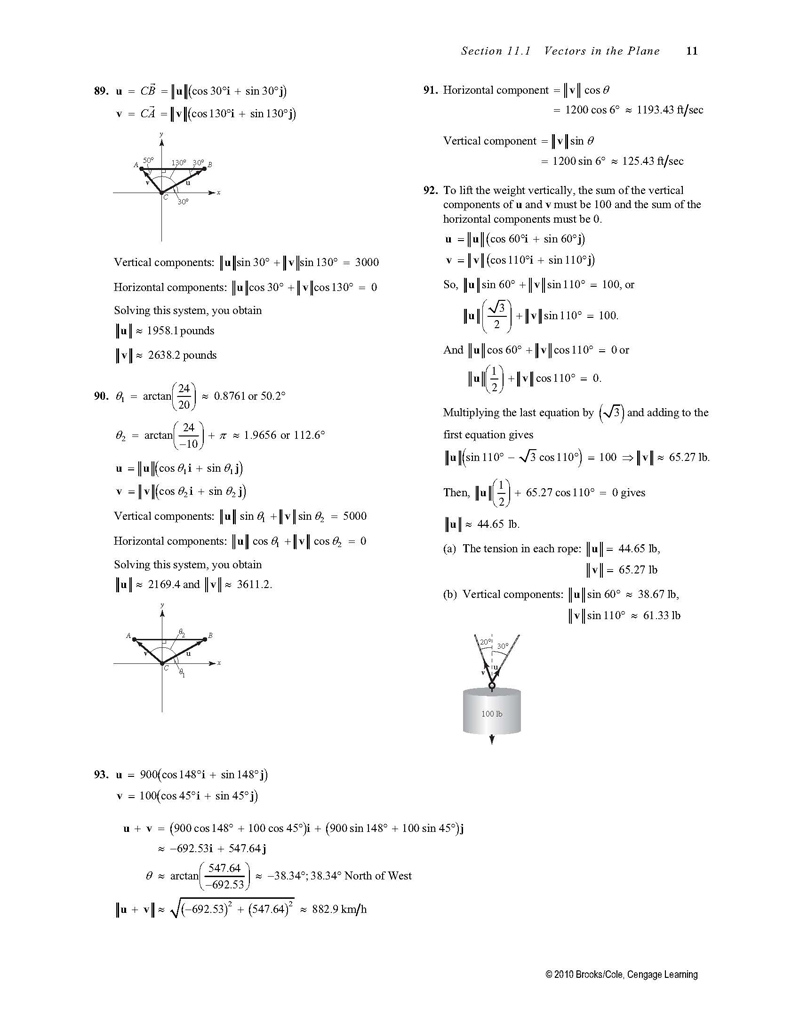
89. u
v
50°
u cos 30qi sin 30q j
v cos 130qi sin 130q j

130° 30° B
91. Horizontal component

Vertical component
v cos T
1200 cos 6q | 1193.43 ft sec

v sin T
1200 sin 6q | 125.43 ft sec
v
C
u
30°
x
92. To lift the weight vertically, the sum of the vertical
components of u and v must be 100 and the sum of the
horizontal components must be 0.
u cos 60qi sin 60q j
Vertical components: u sin 30q v sin 130q
3000
v cos 110qi sin 110q j
Horizontal components: u cos 30q v cos 130q
So, u sin 60q v sin 110q
100, or
Solving this system, you obtain
u | 1958.1 pounds
v | 2638.2 pounds

90. T1 arctan¨ ¸ | 0.8761 or 50.2q
© 20 ¹
arctan¨ ¸ S | 1.9656 or 112.6q
u cos T1 i sin T1 j
v cos T 2 i sin T 2 j
Vertical components: u sin T1 v sin T2
§ 3 ·
¨ 2 ¸ v sin 110q
And u cos 60q v cos 110q

u ¨ ¸ v cos 110q

Multiplying the last equation by
first equation gives
u sin 110q 3 cos 110q 100 ? v | 65.27 lb.

Then, u ¨ ¸ 65.27 cos 110q
u | 44.65 lb.
Horizontal components: u cos T1 v cos T 2
(a) The tension in each rope: u
44.65 lb,
Solving this system, you obtain
u | 2169.4 and v | 3611.2.
y
65.27 lb
(b) Vertical components: u sin 60q | 38.67 lb,
v sin 110q | 61.33 lb
A
v
C
?2

?1
u
B
x
20°

v
30°

Monografias.com

12
u v
v
¸i j
¨
y
c
u
2
a
x
u
v
1
x
2
¬
¼
¬
¼
u
¸i sin¨
v «cos¨ u
¸ cos¨ ¸ cos¨ ¸ j
2 u
¬ ¼
¼
§ T
©
§ T
©
¸ cos¨
¸ cos¨
¸
¸
tan¨ u
©
¸
Chapter 11
Vectors and the Geometry of Space
94.
u
400i plane

400 25 2 i 25 2 j | 364.64i 35.36 j
50 cos 135qi sin 135q j 25 2i 25 2 j wind
tan T
35.36
364.64
? T | 5.54q
Direction North of East: | N 84.46q E
Speed: | 336.35 mi h
95. True

96. True

97. True
102. Let the triangle have vertices at 0, 0 , a, 0 , and
b, c . Let u be the vector joining 0, 0 and b, c , as
indicated in the figure. Then v, the vector joining the
midpoints, is
98. False
a

99. False
b
0
v
§ a b a · c
© 2 2 ¹ 2
b
c
i + j
2
2
(b, c)
( a + b , 2 (
ai bj

100. True
2 a
1
2
bi cj
1
2
u.
(0, 0)
v
( 2 , 0 (
(a, 0)
101.
cos2 T sin 2 T
sin 2 T cos2 T
1,
103. Let u and v be the vectors that determine the
parallelogram, as indicated in the figure. The two
diagonals are u v and v u. So,
r x u v , s 4 v u . But,
r s
u
x u v y v u
y u x y v.
So, x y
1 and x y
0. Solving you have
1 .
x
y
s
u
r
v
104. w
u v v u
u ª v cos T v i v sin T v jº v ª u cos Tu i u sin Tu jº
v ª cos Tu cos T v i sin Tu sin T v jº
ª § T T v · § Tu T v · § Tu T v · § Tu T v · º
¬ © 2 ¹ © 2 ¹ © 2 ¹ © 2 ¹ »
tan T w
sin¨ u

cos¨ u
T v · § Tu
2 ¹ ©
T v · § Tu
2 ¹ ©
T v ·
2 ¹
T v ·
2 ¹
§ T T v ·
2 ¹
So, T w
Tu
T v 2 and w bisects the angle between u and v.
105. The set is a circle of radius 5, centered at the origin.
u
x, y
x 2 y 2
5 ? x 2 y 2
25
© 2010 Brooks/Cole, Cengage Learning

Monografias.com

13
gt .
y
§
¸ g ¨
¸
t
2
g 2
a
2
gx 2
2v0
x
2v0
2v0
2 g
2 g
v0
2
2v0
2 g
v0
2
2
gx 2 gx 2 § v 2 ·
2
gx 2
2v0
gt
2
v2 § g · v 2
2 g © v0
¹
2 g
2
2v0
2v0
2 g
v0
2
3
z
4
2
6
z
2
Section 11.2
Space Coordinates and Vectors in Space
106. Let x
v0t cos D and y
v0t sin D
1 2
2
x
v0 cos D
? y
v0 sin D ¨
©
x · 1 § x ·
v0 cos D ¹ 2 © v0 cos D ¹
x tan D

x tan D
2v0
2 x sec2 D

1 tan 2 D
(x, y)
gx 2 gx 2 v 2
2 2 tan 2 D x tan D 0
gx 2 gx 2 ª § v 2 · v 4 º
2 2 «tan 2 D 2 tan D ¨ 0 ¸ 20 2 »
2v0 ¬ © gx ¹ g x ¼
v0
2 g
2 2 ¨ tan D 0 ¸
2v0 2v0 © gx ¹
2
If y d
v0
2 g
2 , then D can be chosen to hit the point x, y . To hit 0, y : Let D
90q. Then
y
v0t
1 2
2
v0
2 g
2
0 ¨ t 1¸ , and you need y d 0 .
The set H is given by 0 d x, 0 y and y d
v0
2 g
gx 2
2
Note: The parabola y
gx 2
2 is called the “parabola of safety.”
Section 11.2 Space Coordinates and Vectors in Space
1. A 2, 3, 4
B 1, 2, 2
2. A 2, 3, 1
B 3, 1, 4
5.
(5, – 2, 2) – 3
3
4
x
(5, – 2, – 2)
2
1
3
2
1

– 2
– 3
z
1 2
3
y
3.
6
z
6.
z
5
4
8
(2, 1, 3)
(-1, 2, 1)
6
(4, 0, 5)
2
1
x
4
3
2
2 3
4
y
x
6
– 2
– 4
6
y
– 6
(0, 4, – 5)
4.
8
7. x
3, y
4, z
5: 3, 4, 5
(3, -2, 5) 6
8. x
7, y
2, z
1:
7, 2, 1
x
6
y
( 3 , 4, -2(
9. y
0, x
12: 12, 0, 0
10. x
0, y
3, z
2: 0, 3, 2
© 2010 Brooks/Cole, Cengage Learning

Monografias.com

14
4.
2
2
35. ¨
¸
,
,
2 2
§ 3 ·
© 2
¹
2
2
,
,
© 2
¹
2
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
25
2
2
2
2
2
2
2
2
2
Chapter 11
Vectors and the Geometry of Space
11. The z-coordinate is 0.
30. A 3, 4, 1 , B 0, 6, 2 , C 3, 5, 6
12. The x-coordinate is 0.
13. The point is 6 units above the xy-plane.
14. The point is 2 units in front of the xz-plane.
AB
AC
BC
9 4 1
0 1 25
9 1 16
14
26
26
15. The point is on the plane parallel to the yz -plane that
Because AC
BC , the triangle is isosceles.
passes through x 3.
16. The point is on the plane parallel to the xy-plane that
31. A 1, 0, 2 , B 1, 5, 2 , C 3, 1, 1
passes through z
5 2.
AB
0 25 16
41
17. The point is to the left of the xz-plane.
18. The point is in front of the yz-plane.
AC

BC
4 1 9
4 36 1
14

41
19. The point is on or between the planes y
y 3.
3 and
Because AB
BC , the triangle is isosceles.
20. The point is in front of the plane x
32. A 4, 1, 1 , B 2, 0, 4 , C 3, 5, 1
21. The point x, y, z is 3 units below the xy-plane, and
below either quadrant I or III.
22. The point x, y, z is 4 units above the xy-plane, and
above either quadrant II or IV.
AB
AC
BC
Neither
4 1 9
1 36 0
1 25 9
14
37
35
23. The point could be above the xy-plane and so above
quadrants II or IV, or below the xy-plane, and so below
quadrants I or III.
24. The point could be above the xy-plane, and so above
quadrants I and III, or below the xy-plane, and so below
quadrants II or IV.
33. The z-coordinate is changed by 5 units:
0, 0, 9 , 2, 6, 12 , 6, 4, 3

34. The y-coordinate is changed by 3 units:
3, 7, 1 , 0, 9, 2 , 3, 8, 6
25. d
4 0 2 0 7 0
16 4 49 69
§ 5 2 9 3 7 3 ·
© 2 ¹
¨ , 3, 5¸
26. d
2 2
5 3 2 2
§ 4 8 0 8 6 20 ·
36. ¨ ¸
6, 4, 7
16 64 16
96
4 6
37. Center: 0, 2, 5
27. d
6 1 2 2 2 4
25 0 36 61
Radius: 2
x 0 y 2 z 5
28. d
4 2 2
5 2 6 3
38. Center: 4, 1, 1
4 49 9 62
29. A 0, 0, 4 , B 2, 6, 7 , C 6, 4, 8
Radius: 5
x 4 y 1 z 1
AB

AC
22 62 32
62 42 12
49
7

196
14
39. Center:

Radius:
2, 0, 0 0, 6, 0
2
10
1, 3, 0
BC
BC
4 2 15
245 49 196
2
245
AB AC
7 5
x
1 y 3 z 0
10
Right triangle

Monografias.com

15
2
2
2
2
2
2
2
§ 2 81 ·
2
2
©
4 ¹
§ 9 ·
2
©
2 ¹
2
§ 9 ·
© 2
¹
2
2
2
3
3
9
2
2
2
3
0
3
2
2
2
40. Center: 3, 2, 4
Section 11.2
Space Coordinates and Vectors in Space
r
3
tangent to yz-plane
x
3 y 2 z 4
2
9
41.
x
x 2 y 2 z 2 2 x 6 y 8 z 1
2 x 1 y 6 y 9 z 8 z 16
0
1 1 9 16
x
1 y 3 z 4
2
25
Center: 1, 3, 4
Radius: 5
42.
x 2 y 2 z 2 9 x 2 y 10 z 19
0
¨ x 9 x ¸ y 2 y 1 z 10 z 25
2
¨ x ¸ y 1 z 5
19

109
4
81
4
1 25
Center: ¨ , 1, 5¸
Radius:
109
2
43.
9 x 2 9 y 2 9 z 2 6 x 18 y 1
0
x y z
2 x
2 y
1
9
0
x
2

2 x

1
9
y
2
2 y 1 z
2
1
1
9
1
x 1 y 1
z 0
1
Center: 1 , 1, 0
Radius: 1

44. 4 x 2 4 y 2 4 z 2 24 x 4 y 8 z 23
x
2
6 x 9 y y
1
4
z
2
2 z 1
23
4
9
1
4
1
x
3 y
1
2

2
z 1
2
16
Center: 3, 1 , 1
Radius: 4

45. x 2 y 2 z 2 d 36
Solid sphere of radius 6 centered at origin.

46. x 2 y 2 z 2 ! 4
Set of all points in space outside the ball of radius 2 centered at the origin.

Monografias.com

16
47.
2
2
2
x
48.
2
2
2
x
,
,
5
4
3
2
1
z
,
,
z
8
6
4
2
,
3
2
v
Chapter 11
Vectors and the Geometry of Space

x 2 y 2 z 2 4 x 6 y 8 z 13
x2 4 x 4 y 2 6 y 9 z 2 8 z 16
4 9 16 13
2 y 3 z 4 16
Interior of sphere of radius 4 centered at 2, 3, 4 .

x 2 y 2 z 2 ! 4 x 6 y 8 z 13
x2 4 x 4 y 2 6 y 9 z 2 8 z 16
! 13 4 9 16
2 y 3 z 4 ! 16
Set of all points in space outside the ball of radius 4 centered at 2, 3, 4 .
49. (a) v
2 4, 4 2, 3 1
2, 2, 2
53.
4 3, 1 2, 6 0
1, 1, 6
(b) v
2i 2 j 2k
1, 1, 6
1 1 36
38
(c)
-2
– 3
< – 2, 2, 2>
54.
1, 1, 6
Unit vector:
38

1 4, 7 5 , 3 2
1
38
1 6
38 38

5, 12, 5
3
2
1
1
2
3
4
y
5, 12, 5
25 144 25
194
x

50. (a) v
4 0, 0 5, 3 1
4, 5, 2
Unit vector:
5, 12, 5
194
5
194
12
194
5
194
(b) v
(c)
4i 5 j 2h
55.
5 4 , 3 3, 0 1
1, 0, 1
1 1
1, 0, 1
2
< 4, – 5, 2 >
Unit vector:
1, 0, 1
2
1
2
, 0,
1
2
x
6
4
2
2
4
6
y
56. 2 1, 4 2 , 2 4
1, 6, 6
51. (a) v
(b) v
(c)
0 3, 3 3, 3 0
3i 3k
z
< -3, 0, 3>
5
4
-3
3, 0, 3
1, 6, 6 1 36 36
1, 6, 6 1
Unit vector: ,
73 73

57. (b) v 3 1 , 3 2, 4 3
4i j k
(c) v
73
6 6
73 73

4, 1, 1
-2
2
3
1
1
1
2
3
4
y
(a), (d)
5
z
(3, 3, 4)
x
4
3
(0, 0, 0) 2
(-1, 2, 3)
52. (a) v
2 2, 3 3, 4 0
0, 0, 4
– 2
(b) v
4k
(4, 1, 1) 2
4
2
4
y
(c)
4
3
2
1
z
< 0, 0, 4 >
x
x
3
2
1
1
2
3
y
© 2010 Brooks/Cole, Cengage Learning

Monografias.com

17
z
z
4
3
z
8
6
4
2
Q
2
x
6
y
3
3 2
2
2
2
5
8
6
4
2
– 2
1
2
3
y
x
2
2
3
2
2
2
z
2
2
Section 11.2
Space Coordinates and Vectors in Space
58. (b) v
4 2, 3 1 , 7 2
6, 4, 9
62. (a) v
2, 2, 1
(c) v
(a), (d)
6i 4 j 9k

(- 4, 3, 7)
12
9
6
(- 6, 4, 9)
2
1
3
x
3
3
>- 2, 2, -1>
y
x
9
9
y
(b) 2 v
4, 4, 2
(2, -1, – 2)
59. q1 , q2 , q3 0, 6, 2
3, 5, 6
Q
3, 1, 8
>4, – 4, 2>
60. q1 , q2 , q3 0, 2,
1, 4 , 3
5
2
1, 2 , 1
(c)
1 v
6

1, 1,
1
2
z
61. (a) 2 v
2, 4, 4
z
5
4
>1, -1, 1 >
1
3
2
< 2, 4, 4>
x
y
4
-2
2
3
1
1
2
y
(d)
5 v
5, 5,
5
2
x
z
(b) v
1, 2, 2
z

3
< 5, -5, 2 <
2
– 2
– 3
x
6
y
– 3
< – 1, -2, -2>
2
3
63. z
u v
1, 2, 3 2, 2, 1
1, 0, 4
– 2
– 3
64. z
u v 2w
1, 2, 3 2, 2, 1 8, 0, 8
7, 0, 4
(c)
3 v
3 , 3, 3

z
65. z
2u 4v w
2, 4, 6 8, 8, 4 4, 0, 4
6, 12, 6
– 3
-2
-2
– 3
< 3 , 3, 3>
66. z
5u 3v 1 w
x
3
2
– 2
– 3
1
y
5, 10, 15 6, 6, 3 2, 0, 2
3, 4, 20
(d) 0v
0, 0, 0
67. 2z 3u
2 z1 3
2 z1 , z2 , z3 3 1, 2, 3
4 ? z1
7
2
4, 0, 4
-3

x
-2
2
3
1
3
2
1

Monografias.com

18
0
2
i 3 k 2 1 i 3 k and
3
2
2
3
4
j 9 k 3 k .
4
8
3 i 3 1 i 2 j
3 3
K
K
K
K
K
KK
2
K
K
v
2
K
K
K
K
K
Chapter 11
Vectors and the Geometry of Space
68. 2u v w 3z
2 1, 2, 3 2, 2, 1 4, 0, 4 3 z1 , z2 , z3
0, 0, 0
0, 6, 9 3z1 , 3z2 , 3z3
0, 0, 0
0 3z1
0 ? z1
6 3z2
9 3z3
0 ? z2
0 ? z3
2
3
z
0, 2, 3
69. (a) and (b) are parallel because
6, 4, 10 2 3, 2, 5 and
2, 4 , 10 3 3, 2, 5 .

70. (b) and (d) are parallel because
4 j 2 j

2 2 3 4
71. z 3i 4 j 2k
(a) is parallel because 6i 8j 4k 2z.
72. z 7, 8, 3
(b) is parallel because z z 14, 16, 6 .
73. P 0, 2, 5 , Q 3, 4, 4 , R 2, 2, 1
JJJK
PQ 3, 6, 9
JJJ
PR 2, 4, 6
77. A 2, 9, 1 , B 3, 11, 4 , C 0, 10, 2 , D 1, 12, 5
JJJ
AB 1, 2, 3
JJJK
CD 1, 2, 3
JJJK
AC 2, 1, 1
JJJK
BD 2, 1, 1
JJJ JJJK JJJK JJJK
Because AB CD and AC BD, the given points
form the vertices of a parallelogram.
78. A 1, 1, 3 B 9, 1, 2 , C 11, 2, 9 , D 3, 4, 4
JJJ
AB 8, 2, 5
JJJK
DC 8, 2, 5
JJJK
AD 2, 3, 7
JJJ
BC 2, 3, 7
JJJ JJJK JJJK JJJ
Because AB DC and AD BC , the given points
form the vertices of a parallelogram.
3, 6, 9 3 2, 4, 6
JJJK JJJ
So, PQ and PR are parallel, the points are collinear.

74. P 4, 2, 7 , Q 2, 0, 3 , R 7, 3, 9
JJJK
PQ 6, 2, 4
JJJ
PR 3, 1, 2
79. v
v

80. v
v

81. v
0, 0, 0
0

1, 0, 3
1 0 9 10

3j 5k 0, 3, 5
3, 1, 2 1 6, 2, 4
JJJK JJJ
So, PQ and PR are parallel. The points are collinear.

75. P 1, 2, 4 , Q 2, 5, 0 , R 0, 1, 5
JJJK
PQ 1, 3, 4
JJJ
PR 1, 1, 1
JJJK JJJ
Because PQ and PR are not parallel, the points are not
collinear.
76. P 0, 0, 0 , Q 1, 3, 2 , R 2, 6, 4
JJJK
PQ 1, 3, 2
JJJ
PR 2, 6, 4
v

82. v
v

83. v
v

84. v
0 9 25

2i 5 j k
4 25 1

i 2 j 3k
1 4 9

4i 3j 7k
16 9 49
34

2, 5, 1
30

1, 2, 3
14

4, 3, 7

74
JJJK JJJ
Because PQ and PR are not parallel, the points are not
collinear.

Monografias.com

19
7
3
2
7
,
, ,
,
,
¬ ¼
1
z
y
v
z
8
6
3
Section 11.2
Space Coordinates and Vectors in Space
85. v
2, 1, 2
91.
cv
c 2i 2 j k
4c 2 4c 2 c 2
v
4 1 4
3
9c
2
7
(a)
v
v
1
3
2, 1, 2
9c
2

c
49
r 7
(b)
v
v

1
3
2, 1, 2
92.
cu
14c
c i 2 j 3k
4
c 2 4c 2 9c 2
4
86. v
6, 0, 8
14c 2
16
v
36 0 64
10
c
r 8
(a)
v
v
1
10
6, 0, 8
93. v
10
u
u
10
0, 3, 3
3 2
(b)
v
v

1
10
6, 0, 8
10 0,
1
2
1
2
0,
10 10
,
2 2
87. v
v
3, 2, 5
9 4 25
38
94. v
3
u
u
3
1, 1, 1
3
(a)
v
v
1
38
3, 2, 5
3
1
3
,
1
3
,
1
3
3
3
,
3
3
,
3
3
(b)
v
v

1
38
3, 2, 5
95. v
3 u
2 u
3 2, 2, 1
2 3
3 2 2 1
2 3 3 3
1, 1,
1
2
88. v
v
8, 0, 0
8
96. v
7
u
u
7
4, 6, 2
2 14
14 21 7
14 14 14
(a)
v
v
1
8
1, 0, 0
97. v
2ªcos r30q j sin r30q k º
3j r k 0, 3, r1
(b)
v
v
1, 0, 0
8
2
-2
89. (a)–(d) Programs will vary.

(e) u v
4, 7.5, 2
-2
2
-1
1
1

-1
< 0,
3, 1>
u v | 8.732
x
-2
< 0,
3, – 1>
u | 5.099
v | 9.019
98. v
5 cos 45qi sin 45qk
5 2
2
i k or
90. The terminal points of the vectors tu, u tv and
5 cos 135qi sin 135qk
5 2
2
i k
su tv are collinear.
su + tv
5 2
2
(i + k)
5 2
2
(- i + k)
4
2
su
u + tv
6
x
6
y
u
v
tv
99.
v
3, 6, 3
2 v
2, 4, 2
4, 3, 0
2, 4, 2
2, 1, 2
© 2010 Brooks/Cole, Cengage Learning

Monografias.com

20
2
2
3
3

3
2
2
2
4
3
z
1
v
0
8
h
8
8
L2 182
8L
T
T
2
2
2
2
2
2
2
2
0
K K
K K K
K
Chapter 11
Vectors and the Geometry of Space
100.
v
5, 6, 3
108.
r r0
x
1 y 1 z 1
2
2
1, 2, 5
10 ,
2 v
4, 2
10 , 4, 2
13 , 6, 3
x 1 y 1 z 1
This is a sphere of radius 2 and center 1, 1, 1 .
101. (a)
109. (a) The height of the right triangle is h
JJJK
The vector PQ is given by
JJJK
PQ 0, 18, h .
L2 182 .
x
1
u
1
y
The tension vector T in each wire is
(b) w
au bv
ai a b j bk
T
c 0, 18, h where ch
24
3
8.
a 0, a b 0, b 0
So, a and b are both zero.
So, T
0, 18, h and
(c) ai a b j bk
a 1, a b 2, b
w u v
(d) ai a b j bk
a 1, a b 2, b
Not possible
i 2 j k
1

i 2 j 3k
3
182 h 2
h
182 L2 182

, L ! 18.
L2 182
Q (0, 0, h)
102. A sphere of radius 4 centered at x1 , y1 , z1 .
v
x x2 y y1 , z z1
L
x
x1 y y1 z z1
2
4
(0, 18, 0)
x
x1 y y1 z z1
2
16
(0, 0, 0)
18
P
103. x0 is directed distance to yz-plane.
y0 is directed distance to xz-plane.
(b)
L
T
20
18.4
25
11.5
30
10
35
9.3
40
9.0
45
8.7
50
8.6
z0 is directed distance to xy-plane.
104. d
x2
x1 y2 y1 z2 z1
2
(c)
30
L = 18
105.
x
x0 y y0 z z0
2
r 2
T =8
0
100
106. Two nonzero vectors u and v are parallel if u
some scalar c.
cv for
0
x 18 is a vertical asymptote and y
horizontal asymptote.
8 is a
107.
B
(d)
lim
L o18
8L
L2 182
f
C
lim
L of
8L
L2 182
lim
L of
8
1 18 L
2
8
A
JJJ JJJ JJJK
AB BC AC
JJJ JJJ JJJ
So, AB BC CA
JJJK JJJ
AC CA
(e) From the table, T

110. As in Exercise 109(c), x
asymptote. So, lim T
r0 o a
10 implies L 30 inches.

Monografias.com

21
K
z
69
23
69
x
C
AB
AC
K
K
K
F
2
2
2
2
0
§ 2 8
©
3
16 · § 2 1 ·
2
2
9 ¹
©
9 ¹
1
9
§ 4 · § 1 ·
2
©
3 ¹
©
3 ¹
§ 4 1 ·
© 3
3 ¹
Section 11.2
Space Coordinates and Vectors in Space
111. Let D be the angle between v and the coordinate axes.
v cos D i cos D j cos D k
v 3 cos D 1
JJJ
113. AB
JJJK
AC
JJJK
AD
0, 70, 115 , F1
60, 0, 115 , F2
45, 65, 115 , F3
C1 0, 70, 115
C2 60, 0, 115
C3 45, 65, 115
cos D

v
1
3
3
3
3
3
i j k
3
3
1, 1, 1
F
So:
F1 F2 F3 0, 0, 500
60C2 45C3 0
70C1 65C3 0
115 C1 C2 C3 500
0.6
Solving this system yields C1
104 , C
2
28 ,
and
0.4
0.2
(
3
3
,
3
3
,
3
3
(
C3
112 . So:
0.6
0.4
0.2
0.4
y
F1 | 202.919 N
F2 | 157.909 N
F3 | 226.521N
112.
550
302,500
c 2
c 75i 50 j 100k
18,125c 2
16.689655
c | 4.085
F | 4.085 75i 50 j 100k
| 306i 204 j 409k
114. Let A lie on the y-axis and the wall on the x-axis. Then A
JJJ JJJK
AB 8, 10, 6 , AC 10, 10, 6 .

AB
10 2, AC
2 59
JJJ
JJJK
420 JJJJK , F2
650 JJJJJ
Thus, F1
AB
AC
0, 10, 0 , B
8, 0, 6 ,
10, 0, 6 and
F1 F2 | 237.6, 297.0, 178.2 423.1, 423.1, 253.9 | 185.5, 720.1, 432.1
F | 860.0 lb
115. d AP
2d BP
x 2 y 1 z 1
x 1 2
y 2 z 2
x 2 y 2 z 2 2 y 2 z 2
4 x 2 y 2 z 2 2 x 4 y 5
3x 2 3 y 2 3z 2 8 x 18 y 2 z 18
6
16
9
9
¨ x x
¸ y 6 y 9 ¨ z 3 z ¸
44
9

Sphere; center: ¨ , 3, ¸, radius:
2
¨ x ¸ y 3 ¨ z ¸

Monografias.com

22
i
2
2
2
2
1
6
2
2
2
2
2
2
2
2
2
Chapter 11
Vectors and the Geometry of Space
Section 11.3 The Dot Product of Two Vectors
1. u
3, 4 , v
1, 5
6. u
i, v
2

(d) u ? v v 17 1, 5 17, 85
(e) u ? 2v 2 u ? v 2 17 34

(d) u ? v v 22 2, 3 44, 66
(e) u ? 2v 2 u ? v 2 22 44
(a) u ? v 3 1 4 5 17
(b) u ? u 3 3 4 4 25
(c) u 32 42 25

2. u 4, 10 , v 2, 3
(a) u ? v 4 2 10 3 22
(b) u ? u 4 4 10 10 116
(c) u 42 102 116
(a) u ? v 1
(b) u ? u 1
(c) u 1
(d) u ? v v i
(e) u ? 2v 2 u ? v 2

7. u 2i j k , v i k
(a) u ? v 2 1 1 0 1 1
(b) u ? u 2 2 1 1 1 1
(c) u 22 1 12 6
(d) u ? v v v i k
(e) u ? 2v 2 u ? v 2
3. u = 6, 4 , v 3, 2
(a) u ? v 6 3 4 2 26
(b) u ? u 6 6 4 4 52
(c) u 62 4 52
(d) u ? v v 26 3, 2 78, 52
(e) u ? 2v 2 u ? v 2 26 52
8. u 2i j 2k , v i 3j 2k
(a) u ? v 2 1 1 3 2 2
(b) u ? u 2 2 1 1 2 2
(c) u 22 12 2 9
(d) u ? v v 5 i 3j 2k
(e) u ? 2v 2 u ? v 2 5
5
9

5i 15 j 10k
10
4. u
4, 8 , v
7, 5
9.
u ? v
u v
cos T
(a) u ? v
(b) u ? u
4 7 8 5
4 4 8 8
12
80
u ? v
8 5 cos
S
3
20
(c) u
(d) u ? v v
(e) u ? 2v
4 2 82
12 7, 5
2 u ? v
80

84, 60
2 12
24
10.
u ? v
u v

u ? v
cos T

40 25 cos
5S
6
500 3
5. u
2, 3, 4 , v
0, 6, 5
11. u
1, 1 , v
2, 2
(a) u ? v
(b) u ? u

29
cos T

T
u ? v
u v
S
2
0
2 8
0
(d)
u ? v v
2 0, 6, 5
0, 12, 10
12. u
3, 1 , v
2, 1
(e) u ? 2v
2 u ? v
2 2
4
cos T
u ? v
u v
5
10 5
1
2
T
S
4
© 2010 Brooks/Cole, Cengage Learning

Monografias.com

23
3
2
,
6
§ 1 ·
arccos¨ ¸ | 98.1q
1 ,
2
3
2
T
§ S · § S ·
©
6 ¹
© 6 ¹
§ 3S · § 3S ·
© 4 ¹
© 4 ¹
1
2
u
v
j
3
6
¨
2 ©
¹
©
¹
3

T
cos T
S
0
0
arccos¨
©
¹
T
cos T
T
arccos¨
©
¹
5 3
5
AC
CA
BC
CB
3
5
3
3 21
14
2 2
K K
K
2
K
2 2 2 2
K
K K
2
K K
Section 11.3
The Dot Product of Two Vectors
13. u
3i j, v
2i 4 j
20. u
2, 18 , v
1
cos T
u ? v
u v
2
10 20
1
5 2
u z cv ? not parallel
u ? v 0 ? orthogonal
© 5 2 ¹
21. u 4, 3 , v
u z cv ? not parallel
14.
cos¨ ¸i sin¨ ¸ j

cos¨ ¸i sin¨ ¸ j
3
2

i j
2

i
2
2
2
u ? v

22. u
u
0 ? orthogonal
1 i 2 j , v 2i 4 j
1 v ? parallel
cos T
u ? v
u v
3 § 2 · 1 § 2 ·
¨ 2 ¸ 2 ¨ 2 ¸
2
4
1
23. u j 6k , v i 2 j k
u z cv ? not parallel
u ? v 8 z 0 ? not orthogonal
Neither
ª 2
arccos «
¬ 4
1
º
3 »
¼
105q
24. u 2i 3j k , v
u z cv ? not parallel
2i j k
15. u
1, 1, 1 , v
2, 1, 1
u ? v
0 ? orthogonal
cos T
u ? v
u v
2
3 6
2
3
25. u 2, 3, 1 , v 1, 1, 1
u z cv ? not parallel
u ? v 0 ? orthogonal
T
arccos
2
3
| 61.9q
26. u
cos T , sin T , 1 ,
16. u 3i 2 j k , v
u ? v
u v

T =
2
2i 3j
3 2 2 3 0
u v
v sin T , cos T , 0
u z cv ? not parallel
u ? v 0 ? orthogonal
27. The vector 1, 2, 0 joining 1, 2, 0 and 0, 0, 0 is
perpendicular to the vector 2, 1, 0 joining
17. u
3i 4 j, v = 2 j 3k
2, 1, 0 and 0, 0, 0 :
1, 2, 0 ? 2, 1, 0
cos T
u ? v
u v
8
5 13
8 13
65
The triangle has a right angle, so it is a right triangle.
28. Consider the vector 3, 0, 0 joining 0, 0, 0 and
§ 8 13 ·
¨ 65 ¸ | 116.3q

18. u 2i 3j k , v i 2 j k
u ? v 9 9
u v 14 6 2 21
§ 3 21 ·
¨ 14 ¸ | 10.9q

19. u 4, 0 , v 1, 1
u z cv ? not parallel
u ? v 4 z 0 ? not orthogonal
Neither
3, 0, 0 , and the vector 1, 2, 3 joining 0, 0, 0 and
1, 2, 3 : 3, 0, 0 ? 1, 2, 3 3 0
The triangle has an obtuse angle, so it is an obtuse triangle.
29. A 2, 0, 1 , B 0, 1, 2 , C 1 , 3 , 0
JJJ

Partes: 1, 2

Página siguiente