
• • 1 Estructuras III Introducción a los
Elementos Finitos Introducción1 El campo de la
mecánica se puede dividir en 3 grandes áreas: 1.
Teórica 2. Aplicada 3. Numérica El área
teórica se encarga de estudiar las leyes y principios de
la mecánica por su valor científico. Por ejemplo
las leyes de Newton y las leyes de la cinemática entre
otras. El área aplicada transfiere los conocimientos
teóricos a las aplicaciones científicas e
ingenieriles. En general esa transferencia de conocimientos es
utilizada para la generación de modelos matemáticos
que representen a los fenómenos físicos. El
área numérica aparece para resolver aquellos
problemas que son difíciles de resolver
analíticamente. Hoy en día los avances de la
computación permiten resolver de ésta manera
algunos problemas de manera muy sencilla. El resultado obtenido a
partir de la resolución numérica utilizando a la
computación como herramienta de apoyo es lo que se define
como “mecánica computacional”. Los resultados
obtenidos a partir de la mecánica compuacional
deberán ser interpretados teniendo en cuenta la
evolución de los fenómenos físicos.
Mecánica computacional Se puede hacer una división
de los grupos que forman la mecánica computacional
según la escala física del fenómeno que se
quiere estudiar: Nano mecánica y micro mecánica
Mecánica del continuo o Sólidos y estructuras o
Fluidos o Multi físicos (sólido – fluido) El
primero de estos se encarga de los fenómenos a nivel
molecular y atómico. Las leyes que gobiernan estos modelos
son aquellas relacionadas con la física y la
química. La micro mecánica se encarga
principalmente de los fenómenos físicos a niveles
cristalográficos y granulares. La parte de la
mecánica del contínuo estudia los fenómenos
físicos a nivel macroscópico. Las áreas
tradicionales de este último campo son la de los
sólidos y los fluidos. Problemas estáticos y
dinámicos Los problemas de mecánica del continuo se
pueden dividir de acuerdo a los efectos inerciales a ser tenidos
en cuenta: • Estáticos • Dinámicos En los
problemas dinámicos existe una dependencia del tiempo, en
estos problemas las fuerzas inerciales son parte del problema. En
los problemas estáticos o cuasi estáticos las
fuerzas inerciales son nulas o despreciables. Felippa –
Introduction to finite element method Página 1/29

2 2 Estructuras III Introducción a los Elementos Finitos
Comportamientos lineales y no lineales Llamaremos a los problemas
lineales, a aquellos en los la respuesta a una
perturbación del sistema (estructura con cargas aplicadas)
responde a una relación lineal con el valor de la
perturbación. Los problemas no lineales pueden asociarse
al comportamiento del material y a la geometría del
modelo. Alcance de este estudio Con lo visto anteriormente
podemos realizar un desglose de los campos que queremos cubrir en
este curso: • Mecánica o Computacional Del continuo
• Sólidos – estructuras o Estáticos
Lineales Muchos problemas de ingeniería involucran una
complejidad tal que nos vemos forzados a realizar un modelo
matemático que represente al fenómeno
físico. Una manera sencilla de simplificar el modelo es
sub dividir el problema en partes o elementos para luego volverlo
a construir ensamblando las partes para predecir el
comportamiento del sistema completo. Por ejemplo, una estructura
como la de la figura que sigue. Aquí se tiene un
reticulado isoestáticamente restringido. Para su
resolución será necesario separar la estructura en
dos partes, resolver los subsistemas, que se pueden equilibrar
por si mismos, para luego realizar la reconexión del
sistema para ver obtener el resultado final, que será la
obtención de los esfuerzos en cada uno de sus miembros
considerando los efectos del sistema completo. Oñate
– Una introducción generalizada al método de
los elementos finitos Página 2/29

Estructuras III Introducción a los Elementos Finitos
Elemento 2 P Nodo Elemento 1 P Hay sistemas en los cuales las
partes son claramente diferenciables, estando estas conectadas
por uniones comúnmente llamadas nodos. A tales sistemas se
los denomina discretos. A veces estas divisiones no son posibles
por lo que se llega a un modelo matemático que se
manifiesta en ecuaciones diferenciales (problemas de elasticidad
tridimensional). Este tipo de sistemas recibe el nombre de
sistemas contínuos. En algunos casos la solución
analítica de estos problemas es difícil de
encontrar. Para disminuir la complejidad del problema la
propuesta será recurrir al modelo contínuo con
infinitos grados de libertad a uno de finitos grados de libertad.
Esto es lo que se define como un sistema discreto.
Introducción El método de los elementos finitos
(MEF en castellano o FEM en inglés) es un método de
cálculo utilizado en diversos problemas de
ingeniería, que se basa en considerar al cuerpo o
estructura dividido en elementos discretos, con determinadas
condiciones de vínculo entre sí, generándose
un sistema de ecuaciones que se resuelve numéricamente y
proporciona el estado Página 3/29

• • • • • • • Estructuras III
Introducción a los Elementos Finitos de tensiones y
deformaciones. También se utiliza en matemáticas
como método nodal aproximado para resolver ecuaciones
diferenciales en forma numérica. Es un procedimiento
numérico aplicable a un gran número de problemas
con condiciones de borde impuestas (en las estructuras las
condiciones de borde serian: restricciones y cargas externas).
Varios de estos problemas no tienen solución
analítica o es muy difícil obtenerla, por lo que se
convierte en la única alternativa de resolución.
Con este método se pueden resolver sistemas los cuales no
son fáciles de resolver mediante modelos
matemáticos simples. Existen dos tipos de caminos para su
formulación, basándose en el principio de los
trabajos virtuales, es decir, formulaciones variacionales, o
mediante el método de Garlekin, Método directo o
bien con Raleigh Ritz.. Si bien fue originalmente desarrollado
para el análisis de estructuras, con este método se
pueden representar entre otros, los siguientes fenómenos
físicos: Fenómenos termodinámicos:
distribución de temperaturas en un sólido.
Simulación de efectos dinámicos: Choque de dos
cuerpos. Geomecánica: Comportamiento de la corteza
terrestre. Concepto La base del método de los elementos
finitos es la representación de un cuerpo por un ensamble
de subdivisiones llamadas elementos. Estos elementos se
interconectan a través de puntos llamados nodos. Una
manera de discretizar un cuerpo o estructura es dividirla en un
sistema equivalente de cuerpos pequeños, tal que su
ensamble representa el cuerpo original. La solución que se
obtiene para cada unidad se combina para obtener la
solución total. Por ende, La solución del problema
consiste en encontrar los desplazamientos de estos puntos y a
partir de ellos, las deformaciones y las tensiones del sistema
analizado. Las propiedades de los elementos que unen a los nodos,
están dadas por el material asignado al elemento, que
definen la rigidez del mismo, y la geometría de la
estructura a modelizar (a partir de las Leyes de la
Elástica). Las deformaciones y las fuerzas externas se
relacionan entre si mediante la rigidez y las relaciones
constitutivas del elemento. Trabajando en régimen
elástico, las ecuaciones que definen el sistema pueden
expresarse de forma matricial como se muestra a
continuación: [K] .{d}={F} Donde : [K]: es la matriz
rigidez del sistema {d}: es el vector desplazamientos {F}: es el
vector de esfuerzos Los tipos de elementos utilizados
generalmente en la resolución a través de Fem son:
Elementos Lineales (1-D) Página 4/29

• • Estructuras III Estos pueden ser: o o o o Resorte
Barras Vigas Caños Introducción a los Elementos
Finitos Elementos Planos (2-D) Estos pueden ser: o o membranas
placas Elementos Sólidos (3-D) Es importante destacar que
se puede utilizar combinaciones de estos elementos actuando en
conjunto. Proceso de Análisis por Elementos Finitos El
proceso de análisis por elementos finitos se puede
describir como: Página 5/29

• • • • • • Estructuras III
Introducción a los Elementos Finitos Modelado
Geométrico Modelado de Elementos Finitos Definición
del Ambiente Análisis Corroboración de Resultados
Modelado Geométrico: Creación del modelo
matemático del objeto o del conjunto. Reproducción
del sólido en forma precisa y de la geometría de la
superficie. Modelado de Elementos Finitos: Subdividir la
geometría del modelo en elementos discretos. Asignar las
propiedades del material y del elemento. Definición del
Ambiente: Aplicar las cargas y las condiciones de borde para
simular el ambiente de la operación. Análisis:
Computar los resultados (tensiones, deformaciones, etc.) a partir
de análisis estáticos, dinámicos o de
transferencia de calor. Corroboración de Resultados:
Comparar los resultados con los criterios de diseño.
Rediseñar la estructura y repetir el proceso si fuese
necesario. En la actualidad la utilización de este
método ha crecido notablemente debido a la
utilización de software avanzado (además de un
hardware potente que debe poseer gran velocidad y mucha memoria).
Cabe destacar que la utilización de software no implica la
obtención del resultado exacto y real, es solo una
aproximación y esta en el criterio del usuario el saber
discernir entre un resultado coherente y uno que no lo es;
además de conocer los márgenes de error y las
limitaciones del modelo y el método. Método Directo
Elemento Resorte Página 6/29

• • • • • ? ? ? ? ? = ? ?.? ? ? ? ? ? ?
? ?? ? ? – k ? ? ? Estructuras III Introducción a los
Elementos Finitos Los elementos tipo resorte más sencillos
son definidos solamente con rigidez en sentido longitudinal del
mismo, o sea son capaces de resistir esfuerzos de tracción
– compresión. El elemento se define con las
siguientes características: Eje de coordenadas local: x
Nodos: i, j Desplazamientos de los nodos (grados de libertad):
ui, uj Fuerzas internas: fi, fj Rigidez del elemento: k Se debe
recordar que las fuerzas del sistema podrán actuar
solamente en los nodos de los elementos. Las fuerzas internas del
resorte se pueden expresar en función de los
desplazamientos nodales y la rigidez del elemento: Ke fi = Ke (ui
– uj) fj fi fj = Ke (uj – ui) x Se puede expresar este sistema de
forma matricial. Las fuerzas internas como un vector columna
llamado f, así como el vector de los desplazamientos
nodales (u): fi ui f= fj , u= uj Los desplazamientos contemplados
en el modelo matemático (en la dirección x del
elemento) serán los grados de libertad del elemento (GL).
Cuando alguno de estos desplazamientos es una condición de
borde (desplazamiento conocido) este GL pasa a ser un dato del
sistema; pasando entonces a ser la fuerza en el nodo la
incógnita a resolver en el mismo. ? fi? ? k ? fj ? ?- k –
k ? ?ui? k ? ?uj? Siendo ? k ?- k ? la matriz rigidez del
elemento. k ? Debe observarse que la matriz rigidez es
simétrica de modo que se cumpla el equilibrio del sistema
de fuerzas del elemento. Página 7/29

• Donde Estructuras III Introducción a los Elementos
Finitos La matriz del elemento es cuadrada, el orden de la misma
se relaciona directamente con la cantidad de grados de libertad.
Para el elemento definido anteriormente la matriz rigidez es de
orden 2. Sistema de Resortes Considerando un par de resortes en
serie: Para el Elemento 1: Para el Elemento 2: es la fuerza
interna local del Nodo i actuando en el Elemento m (i=1,2).
Considerando la condición de equilibrio estático de
fuerzas: F externas = F internas Nodo 1: Nodo 2: Nodo 3:
Desarrollando con los valores de las fuerzas internas en
función de la rigidez de cada elemento: Página
8/29

Estructuras III De forma Matricial: Introducción a los
Elementos Finitos O bien, Donde: K.U=F K: es la matriz rigidez
del sistema completo de resortes Se puede plantear por separado y
luego plantear superposición: Planteando
superposición se obtiene: A modo de ejemplo si
consideramos un sistema que posee las siguientes condiciones:
Página 9/29

• Estructuras III Introducción a los Elementos
Finitos Reemplazando: Se reduce a: Y, Como incógnita
tenemos: Resolviendo, Reemplazando se obtiene la fuerza de
reacción: Como conclusión, para un sistema de
“n” nodos, el método de elementos finitos
permite generar “n” ecuaciones, las cuales
deberán tener “n” incógnitas para ser
un sistema definido. Las incógnitas podrán ser
parte del vector desplazamiento o ser parte del vector fuerza.
Cada nodo deberá tener su desplazamiento o su fuerza
actuante como condición de borde impuesta. Este sistema
permite, cómo veremos más adelante resolver
sistemas isoestáticos e hiperestáticos sin
necesidad de cambiar el método. Elemento barra en una
dimensión Consideremos una barra de sección
constante: Página 10/29

• Estructuras III El sistema se compone de:
Introducción a los Elementos Finitos • • •
• Dos Nodos: Modulo de Elasticidad Área de la
Sección Transversal Longitud del Elemento i, j E A L El
mismo está sujeto a: • Fuerzas internas: fi, fj El
elemento tiene dos grados de libertad, en el sentido longitudinal
del elemento, cualquier desplazamiento de los nodos en el sentido
normal al elemento no generara esfuerzos internos: Dos
desplazamientos: ui, uj Sabiendo que la rigidez a tracción
/ compresión de una barra es: Y haciendo una
analogía con el elemento resorte, tenemos que: Por lo
tanto, O bien, Por lo tanto, la ecuación de equilibrio del
Elemento será: Para la resolución de este sistema
se procede de la misma manera que en el elemento resorte.
Página 11/29

• Estructuras III Elemento Barra en Dos Dimensiones
Introducción a los Elementos Finitos Local x,y
ui´,vi´ Global X,Y ui,vi 1 grado de Libertad por 2
grados de Libertad por nodo nodo Nota: El desplazamiento lateral
vi´ no contribuye a la deformación de la barra. La
idea es trabajar con las coordenadas globales, por lo tanto se
deben hacer las siguientes transformaciones: Donde: Escrito en
forma matricial: Página 12/29

Estructuras III Introducción a los Elementos Finitos O
bien, Donde la matriz transformación: Donde la
relación con la matriz ortogonal: A modo de ejemplo, se
puede decir que para un sistema de elemento barra con dos nodos
tenemos que: O bien, Con, Las fuerzas nodales son transformadas
de la misma manera: Para obtener la matriz rigidez en dos
dimensiones: En el sistema local de coordenadas tenemos que: Esto
se puede escribir en su totalidad como: Página 13/29

Estructuras III Introducción a los Elementos Finitos O
bien, Utilizando las transformaciones Obtenemos: Multiplicando
ambos lados por TT y como TT*T=I , obtenemos: La matriz rigidez
en el sistema global quedara de la siguiente manera: La cual es
una matriz simétrica de 4X4. Escrita de manera explicita
tenemos que: Donde los cosenos directores l y m son:
Página 14/29

• • • • • Estructuras III
Introducción a los Elementos Finitos Elemento Viga Se
considera una viga en el plano. Esta toma esfuerzos de Corte,
Axiles y Momentos, todas consideradas en el plano. Cada Nodo
posee tres Grados de Libertad (u, v, q). Un elemento que toma
estas cargas, tiene asociado para el calculo a E, J, l y A. El
sistema se compone de: • • • • • Dos
Nodos: Modulo de Elasticidad Área de la Sección
Transversal Longitud del Elemento Momento de Inercia i, j E A L I
El mismo está sujeto a: Fuerzas internas en los Nodos:
Momento en los Nodos: Habrá tres grados de libertad por
cada nodo Cuatro desplazamientos: Dos Giros: Fi, Fj, Vi, Vj Mi,
Mj ui, uj, vi, vj ?i, ?j Para crear la Matriz Rigidez se suponen
casos con desplazamientos unitarios, que luego mediante
Superposición se ensamblan y dan forma a dicha matriz. Se
adoptan giros en sentido horario y desplazamientos positivos. Se
supone ui=1 uj, vi, vj, ?i, ?j =0 Página 15/29

Estructuras III Introducción a los Elementos Finitos
Aplicando la Ley de Hooke, tal como se hace con elemento barra,
tenemos que: Por lo tanto, Hi = EA l · ui Realizando un
equilibrio de fuerzas, Hi = EA l Hj = – EA l Se supone vi =1 ui,
uj, vj, ?i, ?j = 0 Mi Mj Se puede demostrar calculando por
Método de las Fuerzas que para un Desplazamiento
Transversal en el extremo i, los esfuerzos en el sistema son: Vi
= 12EJ l3 M i = – 6EJ l 2 Página 16/29
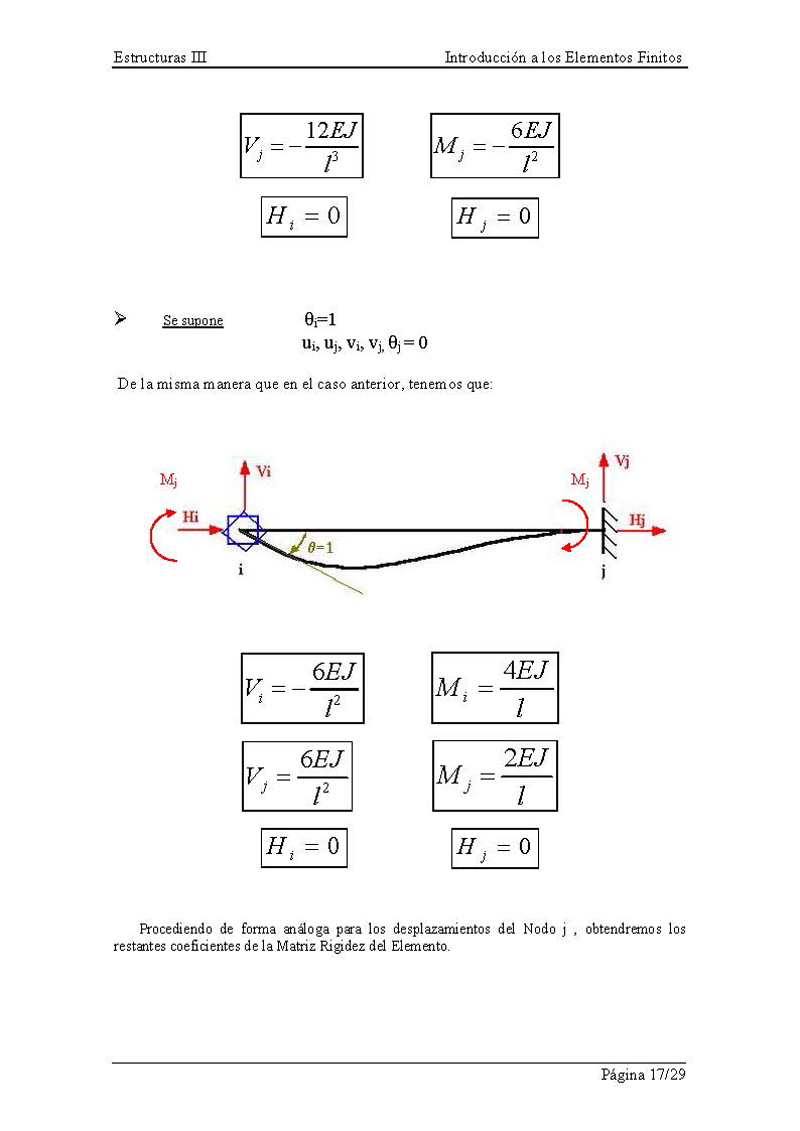
Estructuras III Introducción a los Elementos Finitos V j =
– 12EJ l 3 M j = – 6EJ l 2 H i = 0 H j = 0 Se supone ?i=1 ui, uj,
vi, vj, ?j = 0 De la misma manera que en el caso anterior,
tenemos que: Mj Mj Vi = – 6EJ l 2 M i = 4 EJ l V j = 6EJ l 2 M j
= 2EJ l H i = 0 H j = 0 Procediendo de forma análoga para
los desplazamientos del Nodo j , obtendremos los restantes
coeficientes de la Matriz Rigidez del Elemento. Página
17/29

Estructuras III Introducción a los Elementos Finitos
Ejemplos Prácticos 1. Elemento Resorte Sea un sistema de
resortes en serie, con una carga P aplicada: Datos: Se pide: a)
Encontrar la matriz rigidez del sistema. b) Desplazamientos en
los Nodos 2 y 3. c) Las fuerzas en los empotramientos (Nodos 1 y
4). d) La fuerza en el resorte 2. Solución a) La matriz
rigidez de cada elemento es: Página 18/29

Estructuras III Introducción a los Elementos Finitos
Aplicando el principio de superposición se obtiene la
matriz rigidez del sistema completo: o bien, La Ecuación
Matricial de Equilibrio quedara de la siguiente manera:
Página 19/29

Estructuras III Introducción a los Elementos Finitos b)
Aplicando las Condiciones de Borde: en la Ecuación
Matricial de Equilibrio y tachando la primera y cuarta fila y
columna, tenemos que: Cuya solución es: c) Con la primera
y cuarta fila de la Ecuación de Equilibrio, y con los
datos de los desplazamientos ya calculados, tenemos que: d) La
ecuación de equilibrio del elemento 2 es: donde, Por lo
tanto se puede calcular, la fuerza como: Página
20/29

Estructuras III Introducción a los Elementos Finitos 2.
Sistema de Resortes Sea un sistema de resortes en serie-paralelo
con cargas aplicadas: Se pide: Para el Sistema de Resortes de la
figura, cuyos nodos fueron numerados de forma arbitraria,
encontrar la Matriz Rigidez Global. Solución: Se construye
una Tabla de Conectividad de Elementos: La matriz rigidez de cada
elemento: Página 21/29

Estructuras III Introducción a los Elementos Finitos Por
lo tanto, aplicando el Principio de Superposición,
obtendremos la Matriz Rigidez Global del Sistema: 3. Elemento
Barra Sean dos barras de igual Longitud, igual Modulo de
Elasticidad y el Área de una es dos veces la de la otra:
Se pide: Hallar el desplazamiento en el Nodo 2. Solución:
Página 22/29

Estructuras III Introducción a los Elementos Finitos La
Matriz Rigidez de cada elemento: Elemento 1 Elemento 2 Aplicando
el Principio de Superposición, obtenemos la Matriz Rigidez
Global, y así, obtenemos la Ecuación de Equilibrio.
Aplicando las Condiciones de Borde: y reemplazando, se obtiene:
Para hallar el desplazamiento en el Nodo 2, utilizamos solo la
segunda fila: Página 23/29

Estructuras III Introducción a los Elementos Finitos Por
lo tanto, 4. Elemento Barra en Dos Dimensiones Sean dos barras
idénticas que poseen el mismo Modulo de Elasticidad, la
misma Área Transversal y la misma Longitud: Se pide:
Hallar el desplazamiento del Nodo 2. Solución: En el
sistema Local de Coordenadas, la matriz rigidez de los elementos
es: Estas matrices no pueden ser ensambladas juntas, ya que cada
una esta en diferentes Sistemas Coordinados. Por esta
razón se debe trabajar con un Sistema Coordenado Global.
Trabajaremos con cada elemento por separado: Página
24/29

Estructuras III Introducción a los Elementos Finitos
Elemento 1: La matriz rigidez del elemento 1 respecto a la Terna
Global es: Elemento 2: La matriz rigidez del elemento 1 respecto
a la Terna Global es: Aplicando el Principio de
Superposición, podemos armar la Ecuación de
Equilibrio: Página 25/29

Estructuras III Introducción a los Elementos Finitos
Utilizando las Condiciones de Borde: Consideramos solo la tercer
y cuarta fila, junto a la tercer y cuarta columna, y obtenemos:
Resolviendo: 5. Elemento Viga Sea una viga empotrada-empotrada,
con una carga P aplicada en L/2 y un Momento actuando en el mismo
punto: Se pide: a) Hallar la Rotación y Deflexión
del Nodo 2. Página 26/29

Estructuras III Introducción a los Elementos Finitos b)
Hallar las Reacciones de Vinculo en los Empotramientos. Nota:
Para este ejemplo, se tomo como convención que el momento
antihorario es positivo. No solo como condición de borde,
sino en el análisis matricial, y es por eso que la matriz
rigidez difiere en signos con la de la explicación de la
pagina 15. Solución: a) La Matriz Rigidez de cada Elemento
es: La Ecuación de Equilibrio Global es: Página
27/29

Estructuras III Introducción a los Elementos Finitos
Aplicando las Condiciones de Borde: Reemplazamos y obtenemos: Por
lo tanto, resolviendo: b) Reemplazando en la Matriz Global,
tenemos: Resolviendo tenemos, Página 28/29

• • • • • • Estructuras III
Introducción a los Elementos Finitos Referencias
¨Análisis de Estructuras mediante el Método de
los Elementos Finitos¨. Ing. Ruben Lopez Triaca. Universidad
Nacional del Centro de la Provincia de Buenos Aires.
¨Introduction to Finite Element Method¨. Yijun Liu.
University of Cincinnati. ¨Finite Elements in Solids and
Structures¨. Astley. ¨Resistencia de Materiales¨.
Stiopin “Introduction to finite element method”.
Felippa “Una introducción generalizada al
método de los elementos finitos”. Oñate
Página 29/29