Interaprendizaje de matemática empleando las TIC y el Poliprisma 9.1 (página 2)

Partes: 1, 2

ANEXO Nº 1
FORMATO DE LA ENCUESTA DE DIAGNÓSTICO

UNIDAD EDUCATIVA IBARRA

ENCUESTA DE DIAGNÓSTICO

TEMA: Recursos Didácticos para Matemática

OBJETIVO: Obtener información sobre recursos didácticos de enseñanza de la Matemática
mediante el empleo del presente cuestionario, información que servirá para elaborar recursos
didácticos

INDICACIONES: Estimada/o estudiante señale marcando con una X en la escala que considere
correcto

1 = Totalmente en Desacuerdo
2 = Desacuerdo
3 = Medianamente de Acuerdo
4 = De Acuerdo
5 = Totalmente de Acuerdo

CUESTIONARIO

1) Dados los siguientes recursos didácticos para el interaprendizaje de la Matemática señale su
preferencia sobre la contribución para la enseñanza de la Matemática
Escala
1 2 3 4 5
Recursos didáctico
Pizarrón y tiza
Juegos de razonamiento lógico
Rompecabezas
Libros didácticos con las TIC
Videos

2) Dado los siguientes temas de Matemática, sobre cuáles le gustaría que se elaboren recursos
didácticos para la enseñanza de los mismos.
Temas
Escala 1 2 3 4 5
Aritmética y Algebra
Geometría y Trigonometría
Sistema numérico y de funciones
Probabilidades y Estadística

¡Gracias por su colaboración!

11

?? =
?? =
ANEXO Nº 2
CÁLCULO DEL TAMAÑO DE LA MUESTRA DE DIAGNÓSTICO
Para calcular el tamaño de la muestra suele utilizarse la siguiente fórmula:
?? =
???? 2 ?? 2
(?? – 1)?? 2 + ?? 2 ??2
Donde:
n = el tamaño de la muestra.
N = tamaño de la población.
?? = Desviación estándar de la población que, generalmente cuando no se tiene su valor, suele
utilizarse un valor constante de 0,5.
Z = Valor obtenido mediante niveles de confianza. Es un valor constante que, si no se tiene su valor,
se lo toma en relación al 95% de confianza equivale a 1,96 (como más usual) o en relación al 99% de
confianza equivale 2,58, valor que queda a criterio del encuestador.
e = Límite aceptable de error muestral que, generalmente cuando no se tiene su valor, suele utilizarse
un valor que varía entre el 1% (0,01) y 9% (0,09), valor que queda a criterio del encuestador.

Fuente: Suárez, M. & Tapia, F. (2012). p. 21

Se calculó la muestra para una población de 1000 estudiantes
Como no se tiene los demás valores se tomará ?? = 0,5, Z = 1,96 y e = 0,05.
Remplazando valores en la fórmula se obtiene:
???? 2 ?? 2 500 · 0,52 · 1,962 500 · 0,25 · 3,8416
= =
(?? – 1)?? 2 + ?? 2 ??2 (500 – 1) · 0,052 + 0,5 2 · 1,96 2 (499) · 0,0025 + 0,25 · 3,8416
480,2 480,2
= = 217,49 = 218
1,2475 + 0,9604 2,2079
Los cálculos en Excel se muestran en la siguiente figura:

12

ANEXO Nº 3
ANÁLISIS E INTERPRETACIÓN DE RESULTADOS DE LA ENCUESTA DE DIAGNÓSTICO

Los resultados y cálculos de la pregunta 1 se muestran en la siguiente tabla:
Recurso didáctico
Pizarrón y tiza
Juegos de
Rompecabezas
Libros didácticos
Videos
razonamiento lógico
con las TIC
?? (escala)
1
2
3
4
5
Total
??
210
3
2
3
0
218
????
210
6
6
12
0
234
??
1
2
100
16
99
218
?? · ??
1
4
300
64
495
864
??
2
6
7
40
163
218
????
2
12
21
160
815
1010
??
4
6
8
20
180
218
????
4
12
24
80
900
1020
??
100
60
45
7
6
218
????
100
120
135
28
30
413
% aceptación
21,47
79,27
92,66
93,58
37,89
Donde:
?? = ???????????? ????????????????????
1 = Totalmente en Desacuerdo
2 = Desacuerdo
3 = Medianamente de Acuerdo
4 = De Acuerdo
5 = Totalmente de Acuerdo
Cálculos estadísticos
?? = ????????????????????
???? = ???????????????????? ?????? ???????????? ????????????????????
% ????????????????ó?? = ???????????????????? ???? ????????????????ó?? ???? ???????? ?????????????? ??????á?????????? =
?? = ????????ñ?? ???? ???? ??????????????
?????????? · 100
5 · ??
Los rescursos didácticos con mayor aceptación son los libros didácticos con las TIC con un 93,58 % y los rompecabezas con un 92,66%.

13

Los resultados y cálculos de la pregunta 2 se muestran en la siguiente tabla:
Temas
Aritmética y
Algebra
Geometría y
Trigonometría
Sistema
numérico y de
funciones
Probabilidades
y Estadística
??(????????????)
1
2
3
4
5
Total
??
0
20
80
33
85
218
?? · ??
0
40
240
132
425
837
??
0
0
10
38
166
214
?? · ??
0
0
30
152
830
1012
??
0
0
24
110
84
218
?? · ??
0
0
72
440
420
932
??
0
0
16
30
170
216
?? · ??
0
0
48
120
850
1018
(%)
aceptación
76,79
92,84
85,50
93,39
Donde:
?? = ???????????? ????????????????????
1 = Totalmente en Desacuerdo
2 = Desacuerdo
3 = Medianamente de Acuerdo
4 = De Acuerdo
5 = Totalmente de Acuerdo
Cálculos estadísticos
?? = ????????????????????
???? = ???????????????????? ?????? ???????????? ????????????????????
% ????????????????ó?? = ???????????????????? ???? ????????????????ó?? ???? ???????? ?????????????? ??????á?????????? =
?? = ????????ñ?? ???? ???? ??????????????
?????????? · 100
5 · ??
Los temas de Matemática con mayor aceptación son Geometría y Trigonometría con un 92,84 %, y Probabilidades y Estadística con un 93,39%.

14

ANEXO Nº 4
CERTIFICADO DERECHO DE AUTOR DEL LIBRO
15

ANEXO Nº 5
ISBN DEL LIBRO
http://200.25.180.75/isbn_site/buscador.php?mode=buscar&code=&tit_nombre=Probabilidades+y+
Estad%EDstica+empleando+las+TIC&col_nombre=&tit_IDmateria=&t_idiomas=&tit_date_apar=
&D_sigP=%3D
16

ANEXO Nº 6
ACEPTACIÓN Y PUBLICACIÓN DEL LIBRO EN
WWW. DOCENTESINOVADORES.NET
http://docentesinnovadores.net/Contenidos/Ver/6926#
17

ANEXO Nº 7
ACEPTACIÓN Y PUBLICACIÓN DEL LIBRO EN WWW. MONOGRAFIAS.COM
http://www.monografias.com/trabajos-pdf5/probabilidades-y-estadistica-empleando-
tic/probabilidades-y-estadistica-empleando-tic
18

ANEXO Nº 8
PUBLICACIÓN DEL LIBRO EN WWW. SCRIBD.COM
http://es.scribd.com/doc/237353094/Probabilidades-y-Estadistica-Empleando-Las-TIC
19

ANEXO Nº 9
EL POLIPRISMA 9.1 Y SU GUÍA DIDÁCTICA
20

POLIPRISMA 9.1
ROMPECABEZAS TRIDIMENSIONAL BICOLOR DE 9 PARTES
DEFINICIÓN
Es un rompecabezas tridimensional bicolor integrado por nueve partes prismáticas estratégicamente
pintadas. Para armar el rompecabezas tienen que intervenir todas sus partes, las que pueden
sobreponerse y estar en cualquier plano.
Los prismas que se arman deben tener como base formas triangulares o cuadrangulares y cumplir las
siguientes condiciones:
-Las caras opuestas pintadas de diferente color para prismas de base cuadrangular
-La mitad del rompecabezas pintado de un color y la otra mitad del otro color para el prisma
triangular.
Estas condiciones generan un mayor reto para armar el rompecabezas, ya que cada parte debe estar
en un lugar específico y posición determinada.
PARTES
A continuación se ilustran las nueve piezas prismáticas que integran al Poliprisma 9.1 obtenidas por
partición de un hexaedro
21

??
2
??
2
ESQUEMAS DE LAS PARTES
?? = arista ; (1) = color 1; (2) = color 2

Nota: La medida de la arista (??) puede ser de cualquier valor, y los colores (1 y 2) pueden ser de
cualquier color, pero diferentes entre sí. Los materiales de construcción pueden ser de cualquier
material.

PRISMA TRIANGULAR
(Parte Nº 1)
Tiene las siguientes características:
??
??
2
??
2
v2
2
??
??
2
??
2
a) Sus bases (1.1 y 1.2) son triángulos rectángulos isósceles de lado
b) Su cara lateral 1.3 es un rectángulo de base
v2??
2
y de altura ??
c) Sus caras laterales 1.4 y 1.5 son rectángulos de base
y altura ??
1
d) Este prisma representa del volumen total del Poliprisma 9.1
8

e) Está pintado de la siguiente forma:
-La base superior 1.1 de color (2) y la inferior 1.2 de color (1)
-La caras laterales 1.3, 1.4 y 1.5 de color (2)

22

v2
4
PRISMA TRIANGULAR
(Parte Nº 2)
Tiene las siguientes características:
v2
4
??
v2
4
??
??
??
2
v2
4
??
v2
4
??
a) Sus bases (2.1 y 2.2) son triángulos rectángulos isósceles de lado
1
b) Su cara lateral 2.5 es un rectángulo de base 2 ?? y de altura ??
v2
4
??
c) Sus caras laterales 2.3 y 2.4 son rectángulos de base
?? y de altura ??
1
d) Este prisma representa del volumen total del Poliprisma 9.1
6

e) Está pintado de la siguiente forma:
-La base superior 2.1 de color (2) y la inferior 2.2 de color (1)
-La cara lateral 2.5 de color (2)
-La cara lateral 2.3 de color (2) y la cara 2.4 de color (1)

23

v2
4
PRISMA CUADRANGULAR
(Parte Nº 3)
Tiene las siguientes características:
??
v2
4
??
v2
4
??
v2
4
??
v2
4
??
v2
4
??
a) Sus bases (3.1 y 3.2) son cuadrados de lado
v2
4
??
b) Sus caras lateral 3.3, 3.4, 3.5 y 3.6 son rectángulos de base
?? y de altura ??
1
c) Este prisma representa del volumen total del Poliprisma 9.1
8

d) Está pintado de la siguiente forma:
-La base superior 3.1 de color (2) y la inferior 3.2 de color (1)
-Las caras laterales 3.4 y 3.5 de color (2)
-Las caras laterales 3.3 y 3.6 de color (1)

24

??
2
v2
4
PRISMA TRIANGULAR
(Parte Nº 4)
Tiene las siguientes características:
v2
4
??
v2
4
??
??
v2
4
??
v2
4
??
??
2
a) Sus bases (4.1 y 4.2) son triángulos rectángulos isósceles de lado

y de altura ??
b) Su cara lateral 4.5 es un rectángulo de base
v2
4
??
c) Sus caras laterales 4.3 y 4.4 son rectángulos de base
?? y de altura ??
1
d) Este prisma representa del volumen total del Poliprisma 9.1
6

e) Está pintado de la siguiente forma:
-La base superior 4.1 de color (2) y la inferior 4.2 de color (1)
-La cara lateral 4.5 de color (2)
-Las caras laterales 4.3 y 4.4 de color (1)

25

??
v2
4
v2
4
1
2
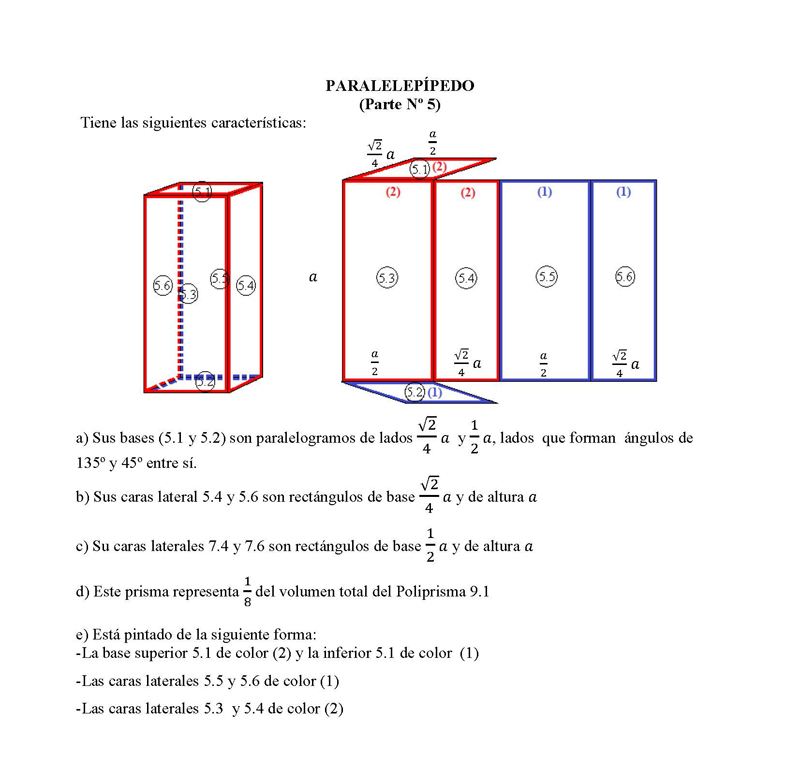
PARALELEPÍPEDO
(Parte Nº 5)
Tiene las siguientes características:
??
v2
4
??
2
??
2
v2
4
??
??
2
v2
4
??
a) Sus bases (5.1 y 5.2) son paralelogramos de lados
135º y 45º entre sí.

b) Sus caras lateral 5.4 y 5.6 son rectángulos de base

c) Su caras laterales 7.4 y 7.6 son rectángulos de base
1
?? y ??, lados que forman ángulos de
2

?? y de altura ??

?? y de altura ??
1
d) Este prisma representa del volumen total del Poliprisma 9.1
8

e) Está pintado de la siguiente forma:
-La base superior 5.1 de color (2) y la inferior 5.1 de color (1)
-Las caras laterales 5.5 y 5.6 de color (1)
-Las caras laterales 5.3 y 5.4 de color (2)

26

??
2
v2
4
16
1
PRISMA TRIANGULAR
(Parte Nº 6)
v2
4
??
v2
4
??
??
??
2
v2
4
??
v2
4
??
a) Sus bases (6.1 y 6.2) son triángulos rectángulos isósceles de lado

y de altura ??
b) Su cara lateral 6.3 es un rectángulo de base
v2
4
??
c) Sus caras laterales 6.4 y 6.5 son rectángulos de base
?? y de altura ??
d) Este prisma representa
del volumen total del Poliprisma 9.1
e) Está pintado de la siguiente forma:
-La base superior 6.1 de color (2) y la inferior 6.2 de color (1)
-La cara lateral 6.4 de color (2)
-Las caras laterales 6.3 y 6.5 de color (1)

27

v2
4
??
2
16
3
PRISMA TRAPECIAL ISÓSCELES
(Parte Nº 7)
Tiene las siguientes características:

??
v2
4
??
2
v2
4
??
??
??
v2
4
??
??
2
v2
4
??
a) Sus bases (7.1 y 7.2) son trapecios isósceles de base mayor ??, base menor
??
2
y de lado
v2
4
??
b) Su cara (7.3) es un cuadrado de lado ??
c) Las caras laterales 7.4 y 7.6 son rectángulos de base
?? y de altura ??
d) La cara lateral 7.5 es un rectángulo de base
y de altura ??
e) Este prisma representa
del volumen total del Poliprisma 9.1
f) Está pintado de la siguiente forma:
-La base superior 7.1 de color (2) y la inferior 7.2 de color (1)
-Las caras laterales 7.3, 7.5 y 7.6 de color (1)
-La cara lateral 7.4 de color (2)

28

PRISMA TRAPECIAL RECTÁNGULO
(Parte Nº 8)
Tiene las siguientes características:
??
v2
4
??
2
v2
4

??
??
v2
4
??
v2
4
??
??
2
v2
2
??
a) Sus bases (8.1 y 8.2) son trapecios rectángulos de base mayor
v2
??
??, y lado
altura
4
2
v2
2
??, base menor
v2
4
??,
b) Su cara lateral 8.6 es un rectángulo de base

c) Su cara lateral 8.5 es un rectángulo de base
v2
?? y de altura ??
2
??
y de altura ??
2
d) Sus caras laterales 8.3 y 8.4 son rectángulos de base
3
e) Su volumen es del volumen total del Poliprisma 9.1
16
v2
4
?? y altura ??
f) Está pintado de la siguiente forma:
-La base superior 8.1 de color (2) y la inferior de color (1)
-Las caras laterales 8.3 y 8.4 de color (2)
-La caras laterales 8.5 y 8.6 de color (1)

29

??
2
v2
4
16
1
PRISMA TRIANGULAR
(Parte Nº 9)
Tiene las siguientes características:
v2
4
??
v2
4
??
??
v2
4
??
??
2
v2
4
??
a) Sus bases (9.1 y 9.2) son triángulos rectángulos isósceles de lado

y de altura ??
b) Su cara lateral 9.4 es un rectángulo de base
v2
4
??
c) Sus caras laterales 9.3 y 9.5 son rectángulos de base
?? y de altura ??
d) Este prisma representa
del volumen total del Poliprisma 9.1
e) Está pintado de la siguiente forma:
-La base superior 9.1 de color (2) y la inferior 9.2 de color (1)
-La cara lateral 9.4 de color (1)
-Las caras laterales 9.3 y 9.5 de color (2)

30

CUERPOS PRISMÁTICOS QUE SE ARMAN CON EL POLIPRISMA 9.1

Los cuerpos prismáticos que se pueden formar al unir las piezas del rompecabezas son: prisma
hexaedro regular o cubo, prisma cuadrangular, prisma rectangular (ortoedro), prisma triangular,
prisma de base trapecial rectángulo, prisma de base trapecial isósceles y prisma de base paralelogramo
(paralelepípedo)
Cubo

Prisma rectangular (Ortoedro)

Prisma trapecial rectángulo
Prisma cuadrangular

Prisma triangular

Prisma trapecial isósceles
Prisma de base paralelogramo (Paralelepípedo)

31

GUÍA DIDÁCTICA PARA EMPLEAR EL POLIPRISMA 9.1
1) ESTRATEGIAS DE INTERAPRENDIZAJE
Con la finalidad de orientar al uso y manejo del Poliprisma se recomienda tener presente los siguientes
aspectos:
El Poliprisma es un recurso didáctico del tipo viso-sensorial que sirve principalmente para reforzar
conocimientos teóricos y desarrollar destrezas y competencias propias en cada estudiante.
El docente debe guiar a sus alumnos para ellos construyan el Poliprisma 9.1 empleando cualquier
medida de la arista y dos colores diferentes entre sí
Presentar al Poliprisma en el espacio y tiempo oportunamente y por procesos, a fin de no desviar la
atención de los estudiantes y así conseguir la plataforma pedagógica, es decir, emplear al
rompecabezas como soporte pedagógico de entrada para motivar a los alumnos al iniciar la clase,
como puente cognitivo a fin de seguir manteniendo el interés durante la clase y como soporte
pedagógico de salida para reforzar la síntesis después al culminar la clase.
No emplear al Poliprisma solamente para armar los diferentes cuerpos geométricos, sino también para
que los estudiantes actúen e investiguen crítica y creativamente, ya que el armar los diferentes cuerpos
geométricos constituye una etapa provisional para llevar al estudiante hasta el pensamiento
matemático, es decir, guiarle hasta la abstracción.
32

4
5
6
9
= 4
2) INSTRUMENTOS EVALUATIVOS
En cuanto a la evaluación se aconseja utilizar la lista de cotejos y el registro de observaciones
sistemáticas. A continuación se presenta estos instrumentos de evaluación, los cuales son flexibles,
por lo que pueden y deben ser adaptados de acuerdo a la realidad del estudiante.

LISTA DE COTEJOS
Datos de Identificación

Institución: Unidad Educativa “Ibarra”
Curso: ………
Asignatura: Matemática
Maestro: Mgs. Mario Suárez
Fecha:…………………

Rasgos a Evaluar
N°
FACTOR
RASGOS
SI
NO
1 Responsabilidad
2 Interés
3 Estilo de trabajo

Aplicación de
destrezas

7 Participación
8 socializada.

10 Actividad
Realiza las actividades correctamente
Es activa/o en clases
Cumple con las tareas establecidas
Arma al Poliprisma buscando diferentes alternativas de
solución
Demuestra perseverancia para obtener datos correctos

Registra y ordena correctamente los resultados

Acepta recomendaciones
Propone tareas en equipo
Busca la unidad grupal
Demuestra creatividad para cumplir lo encomendado
TOTAL

Escala Valorativa
Escala cualitativa
Domina los aprendizajes requeridos
Alcanza los aprendizajes requeridos
Está próximo a alcanzar los aprendizajes requeridos
Escala cuantitativa
9-10
7-8,99
4,01-6,99
No alcanza los aprendizajes requeridos

Juicio del Evaluador
…………………………………………………………………………………………………………
………………………………………………………………………………………………

33

1
2
3
4
5
6
7
8
9
10
11
13
14
15
16
21
22
23
24
27
28
REGISTRO DE OBSERVACIONES SISTEMÁTICAS
Institución: Unidad Educativa “Ibarra”
Curso: …….
Asignatura: Matemática
Maestro: Mgs. Mario Suárez
Fecha:………………..
N°
RASGOS A EVALUAR
ESTUDIANTES
SI
1
NO
SI
2
NO
SI
3
NO
SI
4
NO
SI
5
NO
SI
6
NO
SI
7
NO
SI
8
NO
SI
9
NO
SI
10
NO
Nº de Rasgos a Evaluar
1 Arma al Poliprisma
2 Realiza gráficos
4 Mide correctamente
5 Registra datos
6 Sigue procesos lógicos
7 Resuelve los ejercicios de refuerzo
8 Trabaja en equipo
9 Demuestra perseverancia
10 Demuestra imaginación
12
Escala Valorativa
Escala cualitativa
Escala
cuantitativa
17
18
19
20

25
26
Domina los aprendizajes
requeridos
Alcanza los
aprendizajes requeridos
Está próximo a alcanzar
los aprendizajes
requeridos
No alcanza los
9-10

7-8,99

4,01-6,99

= 4
aprendizajes requeridos
29
30
31
32
33
34
35
36
37
38
39
40

34

3) ENSAYOS EXPERIMENTALES CON EL POLIPRISMA 9.1

3.1) TEOREMA DE PITÁGORAS Y FUNCIONES TRIGONOMÉTRICAS

3.1.1.- Datos de Identificación
Institución: Unidad Educativa “Ibarra”
Integrantes:
Curso:
Fecha:

3.1.2.-Objetivo: Aplicar los conocimientos del Teorema de Pitágoras y de las funciones
trigonométricas a través del Poliprisma 9.1 para calcular los elementos de un prisma trapecial
isósceles.

3.1.3.-Equipo:

3.1.4.-Fundamentos Teóricos

La relación entre los cuadrados de los lados de los triángulos rectángulos se anuncian en el
fundamental Teorema de Pitágoras, cuyo enunciado es el siguiente: En todo triángulo rectángulo el
cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
?? = Hipotenusa
?? = cateto b
?? = cateto a
??2 =
??2 =
??2 =
cuadrado de la hipotenusa
cuadrado del cateto b
cuadrado del cateto a
Del Teorema de Pitágoras se deducen las siguientes conclusiones:
-La hipotenusa es igual a la raíz cuadrada de la suma de los cuadrados de los catetos.
?? = v??2 + ??2
-Un cateto es igual a la raíz cuadrada de la diferencia entre el cuadrado de la hipotenusa y el cuadrado
del otro cateto
?? = v?? 2 – ??2 ?? = v??2 – ??2
Funciones Trigonométricas
Son relaciones entre las longitudes de la hipotenusa y los catetos del triángulo rectángulo. Existen
seis funciones trigonométricas: seno, coseno, tangente, cotangente, secante y cosecante. Las tres
primeras funciones se llaman funciones directas y las tres últimas se llaman funciones recíprocas o
inversas.

35

En el triángulo ACB de la siguiente figura consideramos el ángulo A
c = Longitud de la hipotenusa
a = Longitud del cateto opuesto al ? A
b = Longitud del cateto adyacente al ? A

Las funciones trigonométricas del ángulo A son:
Funciones directas
Funciones inversas
???????? ???? ?? = ?????? ?? =
???????????? ?????????????? ??
=
h?????????????????? ??
?????????????????? ???? ?? = ?????? ?? =
h?????????????????? ??
=
???????????? ?????????????? ??
???????????? ?????????????????? ??
???????????? ???? ?? = ?????? ?? = =
h?????????????????? ??
???????????? ?????????????? ??
???????????????? ???? ?? = ?????? ?? = =
???????????? ?????????????????? ??
h?????????????????? ??
?????????????? ???? ?? = ?????? ?? = =
???????????? ?????????????????? ??
???????????? ?????????????????? ??
???????????????????? ???? ?? = ?????? ?? = =
???????????? ?????????????? ??
Prisma Trapecial Isósceles
Es un cuerpo geométrico limitado por cuatro caras laterales rectangulares y por dos caras trapeciales
isósceles que representan sus bases.

Elementos:

-Aristas: b, c, l, h = altura

-Área lateral = Al = Suma de las 4 áreas de las caras laterales = Perímetro de la base por la altura.
A l = P·h
Perímetro de la base = P y altura = h
-Área total = At = Suma de las 6 áreas de las caras = Área lateral más área de las dos bases
At = P·h + 2B
Área lateral = P·h y área de una base = B

-Volumen = V = Parte del espacio ocupado por el prisma trapecial isósceles = Área de la base por
altura. V=B?h
Área de la base =B y altura = h

36

2 17
17
-Diagonal del cuerpo = D = Hipotenusa del triángulo rectángulo cuyos catetos son la diagonal de la
base y la altura
?? = v??2 + h2

3.1.5.-Proceso

-Unir las partes del Poliprisma para formar el prisma trapecial isósceles de tal manera que las caras
opuestas queden de diferente color.

-Medir 4 veces las aristas b, c, h y el ángulo ? del prisma trapecial isósceles y calcular las medias
aritméticas. Con las medias aritméticas calcular el volumen (V) y la diagonal del cuerpo (D).

3.1.6.- Ejercicios de Refuerzo
N° b( cm) c (cm) h (cm) ? ( o )
( o ) V(cm 3 ) D(cm)
1
2
3
4

3.1.7.-Ejercicios de refuerzo

a) En el siguiente prisma trapecial isósceles comprobar que At = 136 cm 2 , V= 96 cm 3 y sen? =

b) En el siguiente prisma cuya base es un trapecio trisolátero cuyo ángulo en la base superior es 120o
compruebe que At = (40+3 3 )cm2, V= 12 3 cm3 y el ángulo que forma la diagonal del cuerpo con
la diagonal de la base mide 49o 6’ 23.78”

37

.
c) Un hexaedro es cortado para formar el prisma trapecial isósceles como se indica en la siguiente
figura. Si el volumen de la parte sombreada es de 16 cm3 compruebe que el coseno del ángulo formado
por la diagonal del cuerpo con la diagonal de la cara del prisma trapecial isósceles es
5 41
41
d) Un prisma rectangular es cortado para formar el prisma trapecial isósceles como se indica en la
siguiente figura. El volumen del prisma rectangular es de 192 cm 3 y de la parte sombreada es de 48
cm3. Compruebe que a = 6 cm, b = 4 cm, c = 8cm, h = 4 cm

e) En el prisma trapecial isósceles de la figura anterior compruebe que el ángulo que forma la diagonal
del cuerpo con la diagonal de la base del prisma trapecial isósceles es de 25o 14’ 21.85”.

38

C
3.2) TEOREMA DE LOS COSENOS

3.2.1.-Datos de Identificación
Institución: Unidad Educativa “Ibarra”
Integrantes:
Curso:
Fecha:

3.2.2.-Objetivo: Aplicar los conocimientos del Teorema de los Cosenos a través del Poliprisma 9.1
para calcular los elementos de un prisma paralelepípedo.

3.2.3.-Equipo

3.2.4.-Fundamentos Teóricos

Teorema de los Cosenos
En todo triángulo, el cuadrado de la longitud de un lado es igual a la suma de los cuadrados de las
longitudes de los otros dos lados, menos el doble producto de éstos por el coseno del ángulo
comprendido entre dichos lados.
??2 = ??2 + ??2 – 2????????????
??2 = ??2 + ??2 – 2????????????
?? 2 = ??2 + ??2 – 2????????????
??
??
A
??
??
H
??
B
A continuación se demuestra el teorema para el lado a o BC
Consideremos el triángulo anterior .Sea CH el segmento altura y sean m y n las longitudes de los
segmentos en el que el punto h divide el lado AB

Empleando el Teorema de Pitágoras el triángulo AHC y el BHC se obtiene:
??2 = h2 + ??2 (1)
??2 = h2 + ??2 (2)
Al restar la ecuación (2) de la ecuación (1):
??2 – ??2 = ??2 – ??2
Observando en el triángulo ABC se tiene ?? + ?? = ?? ? ?? = ?? – ??
Remplazando ?? = ?? – ?? en la ecuación ??2 – ??2 = ??2 – ??2 sea obtiene:
??2 – ??2 = (?? – ??)2 – ??2
Elevando al cuadrado (?? – ??)2 en la expresión anterior
39

??2 – ??2 = ?? 2 – 2???? + ??2 – ??2
Términos semejantes y transponiendo ??2 de la expresión anterior
??2 = ??2 + ?? 2 – 2????
Observando en el AHC se tiene:
??
???????? =
??
Despejando ?? de la ecuación anterior se obtiene ?? = ???????? · ??
Remplazando ?? = ???????? · ?? en ?? 2 = ?? 2 + ?? 2 – 2????
??2 = ??2 + ?? 2 – 2????????????
En forma similar se demuestra el teorema del coseno para los lados b y c
Paralelepípedo
Es prisma limitado por seis caras rectangulares de dos en dos opuestas iguales y paralelas. Sus bases
son paralelogramos.
Elementos:
-Aristas: l= largo, a = ancho, h = altura
-Área lateral = Al = Suma de las 4 áreas de las caras laterales = Perímetro de la base por la altura.
??l = ?? · h
Perímetro de la base = P y altura = h
-Área total = At = Suma de las 6 áreas de las caras = Área lateral más área de las dos bases
???? = ?? · h + 2??
Área lateral = P·h y área de una base = B
-Volumen = V = Parte del espacio ocupado por el paralelepípedo = Área de la base por altura.
?? = ?? · h
Área de la base =B y altura = h
-Diagonal de la base = d = Lado del triángulo oblicuángulo
??1 = v??2 + l2 – 2??l???????? ?? ??2 = v??2 + l2 – 2??l????????
40

2
2
??
y
-Diagonal del cuerpo = D = Hipotenusa del triángulo rectángulo cuyos catetos son la diagonal de la
base y la altura
??1 = v??1 + h 2
??2 = v??2 + h 2
3.2.5.-Proceso

-Unir las partes del Poliprisma para formar el paralelepípedo de tal manera que las caras opuestas
queden de diferente color.
-Medir 4 veces las aristas a, l, h y el ángulo ? del paralelepípedo. Calcular las medias aritméticas.
Con las medias aritméticas calcular el volumen (V) y las diagonales del cuerpo (D1 y D2).

3.2.6.-Registro de Datos
N° a( cm) l (cm) h (cm) ? ( o )
(cm)
( o )
V(cm 3 )
D(cm)
1
2
3
D 1

D2
4

3.2.7.- Ejercicios de Refuerzo

a) En el siguiente paralelepípedo compruebe que D 1 = 5cm, D 2 = 41 cm, At = 4(3 13 +2 3 )cm2
V = 4 39 cm3
b) En el siguiente paralelepípedo compruebe que D1 = 3,39 cm, D2 = 6,55 cm,
At = 44 cm2 , V
= 12cm3

c) En el siguiente paralelepípedo compruebe que At=22 3 cm2 y V = 12cm3

41

d) En el siguiente paralelepípedo desarrollado (desdoblado) compruebe que
At=4(2 3 +9)cm2 y
V=12 3 cm3 y las diagonales del cuerpo
21 cm y 37 cm
e) Las diagonales de la base de un paralelepípedo miden 80 cm y 100 cm, y el ángulo comprendido
entre ellas es de 300. Si la altura del paralelepípedo mide 20 cm, compruebe que las diagonales del
cuerpo miden 20 17 cm y 20 26 cm, y tiene como volumen 0,04 m 3

42

3.3) TEOREMA DE LOS SENOS

3.3.1.-Datos de Identificación
Institución: Unidad Educativa “Ibarra”
Integrantes:
Curso:
Fecha:

3.3.2.-Objetivo: Aplicar el teorema de los senos a través del Poliprisma 9.1 para calcular los
elementos de un prisma triangular.

3.3.3.-Equipo

3.3.4.-Fundamentos Teóricos

Teorema de los Senos

En todo triángulo ABC, las longitudes de los lados son directamente proporcionales a los senos de
los ángulos opuestos a dichos lados.

?? ?? ??
= =
???????? ???????? ????????

Consideremos al siguiente triángulo oblicuángulo ABC. Tracemos la altura h desde el vértice del
ángulo B hasta el lado AC.

B
??
h
??
A
??
D
C
En el triángulo ADB calculando ????????:
???????? =
h
??
43

(1)
Despejando h
h = ???????? · ?? (1)

En el triángulo CDB calculando ???????? y despejando h:
h
???????? = ? h = ?? · ???????? (2)
??

Aplicando la propiedad transitiva de la igualdad entre las ecuaciones 1 y 2 se tiene:
?? · ???????? = ?? · ????????
Transponiendo ???????? y ???????? se obtiene:
?? ??
=
???????? ????????
Generalizando esta igualdad para el lado B y su lado opuesto:
?? ?? ??
= =
???????? ???????? ????????
Prisma Triangular

Es un cuerpo geométrico limitado por tres caras laterales rectangulares y por dos caras triangulares
que representan sus bases. Es el único prisma que no tiene diagonal de la base ni diagonal del cuerpo.

Elementos:

-Aristas: a = arista a, b = arista b, c = arista c, h = altura

-Área lateral = Al = Suma de las 3 áreas de las caras laterales = Perímetro de la base por la altura
??l = ?? · h
Perímetro de la base = P = y altura = h

-Área total = At = Suma de las 5 áreas de las caras = Área lateral más área de las dos bases
???? = ?? · h + 2??
Área lateral = P·h y área de una base = B

Para calcular el área de la base (área del triángulo) se emplea las siguientes fórmulas:
?? = á?????? ?=
???????? · ????????????
2
?? = á?????? ?=
?? · ?? · ????????
2
(2)
44

(3)
10
3
?
?? = á?????? ?= v?? · (?? – ??) · (?? – ??) · (?? – ??) ???????????? ?? =
?? ?? + ?? + ??
=
2 2
(1) = Ecuación geométrica; (2) = Ecuación trigonométrica; (3) = Ecuación de Herón

-Volumen = V = Parte del espacio ocupado por el prisma triangular = Área de la base por altura.
V=B?h
Área de la base =B y altura = h

3.3.5.-Proceso

-Unir las partes del Poliprisma para formar el prisma triangular de tal manera que la mitad del
rompecabezas quede pintado de un color y la otra mitad del otro color. Sea creativ?.

-Medir 4 veces las aristas a y h y los ángulos A y B del prisma triangular. Calcular las medias
aritméticas de las aristas y los ángulos. Con las medias aritméticas calcular el área total del prisma
triangular.

3.3.6.-Registro de Datos
N° c (cm) h (cm)
At(cm2)
1
2
3
4

3.3.7.- Ejercicios de Refuerzo

a) En el siguiente prisma triangular con c = 10 cm, h = 5 cm, ? = 800 y ? = 300. Compruebe que a =
5,32 cm, c = 10,48 cm, At = 110,2 cm2 y V = 131 cm3
b) En el siguiente prisma compruebe que At =
18 ? 17 3 ? cm2 y V = 100 3 cm3
45

c) En el siguiente prisma compruebe que ?= 82o 24’ 36” y V = 260 3 cm3
d) Compruebe en el siguiente prisma que b = 2m, c = 2 3 m y V = 3 3 m 3
46

ANEXO Nº 10
CERTIFICADO DE DERECHO DE AUTOR DEL POLIPRISMA 9.1
47

ANEXO Nº 11
ACEPTACIÓN Y PUBLICACIÓN DEL POLIPRISMA 9.1 EN
WWW. MONOGRAFIAS.COM
/trabajos-pdf5/poliprisma-9-1-rompecabezas-tridimensional-
bicolor/poliprisma-9-1-rompecabezas-tridimensional-bicolor
48

ANEXO Nº 12
PUBLICACIÓN DEL POLIPRISMA 9.1 EN WWW. SCRIBD.COM
http://es.scribd.com/doc/237352709/Poliprisma-9-1-Rompecabezas-tridimensional-bicolor#
49

ANEXO Nº 13
FOTOS
Fotos del Poliprimas 9.1 en clases
50

Fotos del libro en clases
51

1
2
3
4
5
6
7
8
9
10
ANEXO Nº 14
FORMATO DE LA ENCUESTA DE VALIDACIÓN DEL PROYECTO

UNIDAD EDUCATIVA IBARRA

ENCUESTA DE VALIDACIÓN DEL PROYECTO

Estimada alumna, la presente encuesta tiene por objeto validar el Proyecto “Interaprendizaje de
Matemática Empleando las TIC y el Poliprisma 9.1”
A continuación se presenta una serie de indicadores de contribución del proyecto en el proceso de
interaprendizaje de la Matemática. Señale marcando con una X en la escala que considere correcto

1 = Totalmente en Desacuerdo
2 = Desacuerdo
3 = Medianamente de Acuerdo
4 = De Acuerdo
5 = Totalmente de Acuerdo
Nº
INDICADORES DE CONTRIBUCIÓN DEL PROYECTO
Motivar la clase
ESCALA
1 2 3 4 5
Despertar y mantener la atención
Hacer la enseñanza más activa
Aprender de manera recreativa
Desarrollar la creatividad
Fortalecer el razonamiento lógico-matemático
Desarrollar destrezas
Promover el trabajo intelectual
Favorecer el aprendizaje significativo
Mejorar el interaprendizaje de la Matemática

¡Gracias por su colaboración!

52

?? =
=
ANEXO Nº 15
CÁLCULO DEL TAMAÑO DE LA MUESTRA DE VALIDACIÓN

Para calcular el tamaño de la muestra suele utilizarse la siguiente fórmula:
?? =
???? 2 ?? 2
(?? – 1)?? 2 + ?? 2 ??2
Donde:
n = el tamaño de la muestra.
N = tamaño de la población.
?? = Desviación estándar de la población que, generalmente cuando no se tiene su valor, suele
utilizarse un valor constante de 0,5.
Z = Valor obtenido mediante niveles de confianza. Es un valor constante que, si no se tiene su valor,
se lo toma en relación al 95% de confianza equivale a 1,96 (como más usual) o en relación al 99% de
confianza equivale 2,58, valor que queda a criterio del encuestador.
e = Límite aceptable de error muestral que, generalmente cuando no se tiene su valor, suele utilizarse
un valor que varía entre el 1% (0,01) y 9% (0,09), valor que queda a criterio del encuestador.

Fuente: Suárez, M. & Tapia, F. (2012). p. 21

Se calculó la muestra de una población de 120 estudiantes de 1ro BGU “H” (Pre-BI), 2do BGU “H”
(1ro BI), 3ro BGU “C” y 3ro BGU “D”
Remplazando valores en la fórmula se obtiene:
???? 2 ??2 120 · 0,52 · 1,962 120 · 0,25 · 3,8416
= =
(?? – 1)?? 2 + ?? 2 ?? 2 (120 – 1) · 0,052 + 0,52 · 1,962 (119) · 0,0025 + 0,25 · 3,8416
?? =
115,248
0,2975 + 0,9604
115,248
1,2579
= 91,62 = 92
Los cálculos en Excel se muestran en la siguiente figura:

53

Nº
1
2
3
4
5
6
7
8
10
9
ANEXO Nº 16
ANÁLISIS E INTERPRETACIÓN DE RESULTADOS DE LA ENCUESTA DE VALIDACIÓN

Los resultados y cálculos se muestran en la siguiente tabla:
Nº
1
2
3
4
5
6
7
8
9
10
x (Puntaje)
1
2
3
4
5
Total
??
0
0
1
8
83
92
?? · ??
0
0
3
32
415
450
??
0
0
2
8
82
92
?? · ??
0
0
6
32
410
448
??
0
0
1
9
82
92
?? · ??
0
0
3
36
410
449
??
0
0
2
7
83
92
?? · ??
0
0
6
28
415
449
??
0
0
3
7
82
92
?? · ??
0
0
9
28
410
447
??
0
0
0
2
90
92
?? · ??
0
0
0
8
450
458
??
0
0
0
11
81
92
?? · ??
0
0
0
44
405
449
??
0
0
1
6
85
92
?? · ??
0
0
3
24
425
452
??
0
0
0
10
82
92
?? · ??
0
0
0
40
410
450
??
0
0
0
4
88
92
?? · ??
0
0
0
16
440
456
??(%)
97,83
97,39
97,61
97,61
97,17
99,57
97,61
98,26
97,83
99,13
Sumatoria
Total
%
promedio

Donde:
Indicadores de contribución del Proyecto
Motivar la clase
Despertar y mantener la atención
Hacer la enseñanza más activa
Aprender de manera recreativa
Desarrollar la creatividad
Fortalecer el razonamiento lógico-matemático
Desarrollar destrezas
Promover el trabajo intelectual
980,00

98,00

?? = ???????????? ????????????????????
1 = Totalmente en Desacuerdo
2 = Desacuerdo
3 = Medianamente de Acuerdo
4 = De Acuerdo
5 = Totalmente de Acuerdo
Cálculos estadísticos
?? = ???????????????????? ; ?? = ????????ñ?? ???? ??????????????
???? = ???????????????????? ???????????????????????? ?????? ???? ???????????? ????????????????????
Favorecer el aprendizaje significativo

Mejorar el interaprendizaje de la Matemática
?????????? · 100
??(%) = ???????????????????? ???? ????????????????ó?? ???? ???????? ?????????????????? =
5 · ??
% ???????????????? = ???????????????????? ???????????????? ???? ????????????????ó?? ?????? ???????????????? =
?????????????????? ??????????
??ú???????? ???? ??????????????????????
54

%deAceptación
Graficando los resultados:

VALIDACIÓN DEL PROYECTO
100,00

99,50

99,00

98,50
99,57
98,26
99,13
98,00
97,83
97,61
97,61
97,61
97,83
97,50

97,00

96,50

96,00

95,50
97,39
97,17
1
2
3
4
5
6
7
8
9
10
Indicadores de contribución del Proyecto

Observando los resultados se evidencia que existe un criterio mayoritario del 98% de aceptación promedio, por lo que se infiere que el presente proyecto ayuda
a mejorar el proceso de interaprendizaje de la Matemática.

55