Coeficiente de correlación de Karl Pearson con Excel, Graph y GeoGebra

¯ ¯
¯
¯
¯
¯
COEFICIENTE DE CORRELACIÓN DE KARL PEARSON
Autor: Mario Suárez
mgsmariosuarez@gmail.com

Llamando también coeficiente de correlación producto-momento.

a) Para datos no agrupados se calcula aplicando la siguiente ecuación:
?? =
? ????
v(? ??2 )(? ??2 )
r = Coeficiente producto-momento de correlación lineal

?? = ?? – ?? ; ?? = ?? – ??

Ejemplo ilustrativo:
Con los datos sobre las temperaturas en dos días diferentes en una ciudad, determinar el tipo de
correlación que existe entre ellas mediante el coeficiente de PEARSON.

X 18 17 15 16 14 12 9 15 16 14 16 18 SX =180
Y 13 15 14 13 9 10 8 13 12 13 10 8 SY= 138

Solución:

Se calcula la media aritmética
??¯ =
? ????
??
Para X:
???? =
180
12
= 15
Para Y:
???? =
138
12
= 11,5
Se llena la siguiente tabla:
??
18
17
15
16
14
12
9
15
16
14
16
18
180
??
13
15
14
13
9
10
8
13
12
13
10
8
138
3
2
0
1
-1
-3
-6
0
1
-1
1
3
?? = ?? – ??
1,5
3,5
2,5
1,5
-2,5
-1,5
-3,5
1,5
0,5
1,5
-1,5
-3,5
?? = ?? – ??
????
9
4
0
1
1
9
36
0
1
1
1
9
72
????
4,5
7
0
1,5
2,5
4,5
21
0
0,5
-1,5
-1,5
-10,5
28
????
2,25
12,25
6,25
2,25
6,25
2,25
12,25
2,25
0,25
2,25
2,25
12,25
63

Se aplica la fórmula:
?? =
? ????
v(? ??2 )(? ??2 )
=
28
v(72)(63)
= 0,416
Existe una correlación moderada

En Excel se calcula de la siguiente manera:

a) Se inserta la función COEF.DE.CORREL y pulsar en Aceptar.

b) En el cuadro de argumentos de la función, en el recuadro de la Matriz 1 seleccionar las celdas de X, y
en el recuadro de la Matriz 2 seleccionar las celdas de Y.

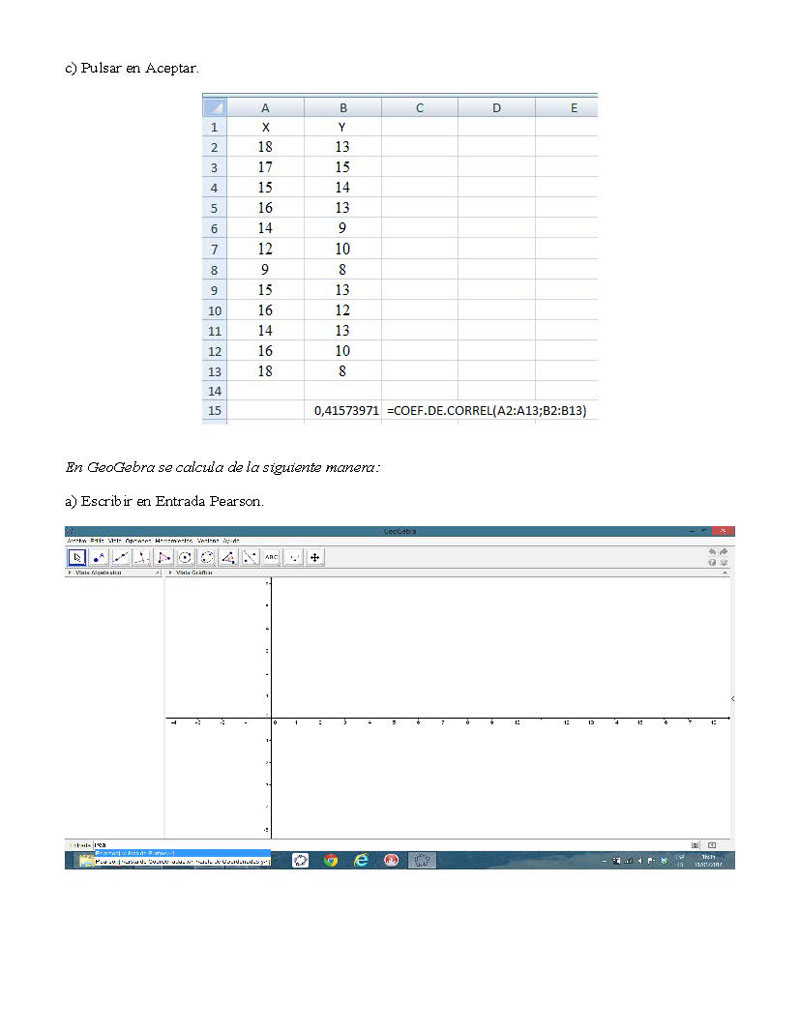
c) Pulsar en Aceptar.
En GeoGebra se calcula de la siguiente manera:
a) Escribir en Entrada Pearson.

b) Seleccione la opción Pearson[ , ]
c) Escribir los datos de X y los datos de Y. Para escribir las llaves utilizar el teclado virtual:
Pearson[ {18, 17, 15, 16, 14, 12, 9, 15, 16, 14, 16, 18}, {13, 15, 14, 13, 9, 10, 8, 13, 12, 13, 10, 8}]

d) Enter
El diagrama de dispersión en Excel se realiza de la siguiente manera:
a) Seleccionar los datos e insertar diagrama de dispersión.

b) En diagrama dispersión, escoger el primero.
c) Para que ver las coordenadas escoger el diseño N° 7.

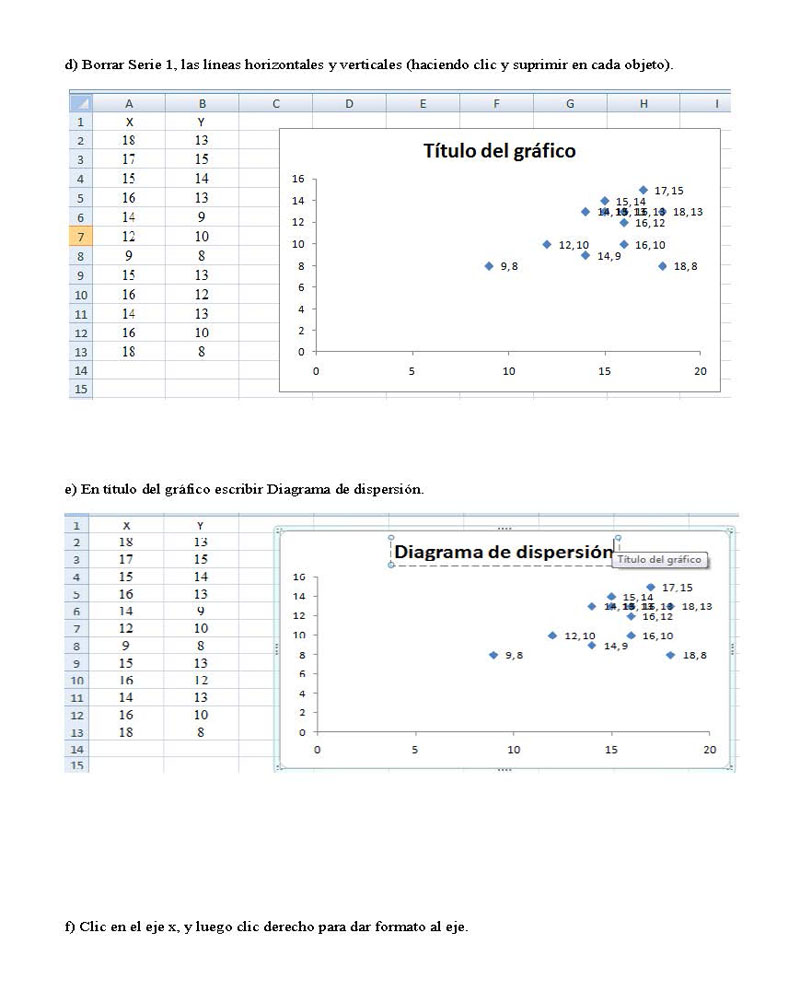
d) Borrar Serie 1, las líneas horizontales y verticales (haciendo clic y suprimir en cada objeto).
e) En título del gráfico escribir Diagrama de dispersión.
f) Clic en el eje x, y luego clic derecho para dar formato al eje.

g) Poner 2 en la casilla unidad mayor para ver los números de 2 en 2 en el eje x.

h) Clic en Cerrar para culminar la elaboración del diagrama de dispersión, aunque se le puede seguir
haciendo más mejoras.
Para realizar el diagrama de dispersión en el programa Graph se procede de la siguiente manera:
a) Clic en Función.

b) Clic en Insertar serie de puntos.
c) Escribir los puntos, y en estilo de línea, escoger sin línea. En rótulos poner en ver coordenadas a la
derecha. Pulsar en Aceptar.

d) Para editar los ejes, hacer clic en Editar y luego en Ejes.
e) Llenar las casillas del Eje X de acuerdo a los datos del ejercicio.

f) Llenar las casillas del Eje Y de acuerdo a los datos del ejercicio.
g) Pulsar en Aceptar para dar por culminado la elaboración del diagrama de dispersión, el cual se
presenta en la siguiente figura:

?? =
b) Para datos agrupados, el coeficiente de Correlación de Pearson se calcula aplicando la siguiente
fórmula:

?? · ? ?? · ???? · ???? – (? ???? · ????) (? ???? · ????)
v[?? · ? ???? · ????2 – (? ???? · ????)2 ][?? · ? ???? · ???? 2 – (? ???? · ????)2 ]
Donde:
?? = número de datos.
?? = frecuencia de celda.
???? = frecuencia de la variable X.
???? = frecuencia de la variable Y.
???? = valores codificados o cambiados para los intervalos de la variable X, procurando que al intervalo
central le corresponda ???? = 0, para que se hagan más fáciles los cálculos.
???? = valores codificados o cambiados para los intervalos de la variable X, procurando que al intervalo
central le corresponda ???? = 0, para que se hagan más fáciles los cálculos.

Ejemplo ilustrativo:
Con los siguientes datos sobre los Coeficientes Intelectuales (X) y de las calificaciones en una prueba de
conocimiento (Y) de 50 estudiantes:
N° de
estudiante
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
X

76
77
78
79
79
80
80
80
82
82
83
83
83
83
84
84
84
85
85
86
86
86
86
87
88
Y

28
24
18
41
43
45
34
18
40
35
30
21
22
23
25
11
15
31
35
26
30
24
16
20
36
N° de
estudiante
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
X

88
88
88
88
89
89
90
90
90
91
92
92
93
93
93
94
96
97
98
99
100
101
101
102
102
Y

40
31
35
26
30
24
18
11
15
38
34
31
33
35
24
40
35
36
40
33
51
54
55
41
45
1) Elaborar una tabla de dos variables
2) Calcular el coeficiente de correlación

Solución:

1) En la tabla de frecuencias de dos variables, cada recuadro de esta tabla se llama una celda y
corresponde a un par de intervalos, y el número indicado en cada celda se llama frecuencia de celda.
Todos los totales indicados en la última fila y en la última columna se llaman totales marginales o
frecuencias marginales, y corresponden, respectivamente, a las frecuencias de intervalo de las
distribuciones de frecuencia separadas de la variable X y Y.

Para elaborar la tabla se recomienda:

– Agrupar las variables X y Y en un igual número de intervalos.

– Los intervalos de la variable X se ubican en la parte superior de manera horizontal (fila) y en orden
ascendente.

– Los intervalos de la variable Y se ubican en la parte izquierda de manera vertical (columna) y en orden
descendente.

Para elaborar los intervalos se procede a realizar los cálculos respectivos:

En la variable X:

Calculando el Rango se obtiene:
?? = ????á?? – ????í?? = 102 – 76 = 26

Calculando el número de intervalos se obtiene:
???? = 1 + 3,32 · ??????(??) = 1 + 3,32 · ??????50 = 6,6 = 7

Calculando el ancho se obtiene:
?? 26
?? = =
???? 6,6
= 3,93 = 4
En la variable Y:

Calculando el Rango se obtiene:
?? = ????á?? – ????í?? = 55 – 11 = 44

Calculando el número de intervalos se obtiene:
???? = 1 + 3,32 · ??????(??) = 1 + 3,32 · ??????50 = 6,64 = 7

Calculando el ancho se obtiene:
?? 44
?? = =
???? 6,64
= 6,62 = 7
Nota: Para la variable X se tomará un ancho de intervalo igual a 4 y para la variable Y un ancho de
intervalo igual a 7. Debe quedar igual número de intervalos para cada variable, que en este ejemplo es
igual a 7.

Calificaciones(Y)
Calificaciones(Y)
????
Contando las frecuencias de celda para cada par de intervalos de las variables X y Y se obtiene la
siguiente tabla de frecuencias de dos variables:

Coeficientes Intelectuales (X)
76-79 80-83 84-87 88-91 92-95 96-99 100-103
53-59
46-52
2
1
2
1
39-45
32-38
25-31
18-24
2

1
2
2
2
1
4
1
4
2
1
3
3
2
1
3
1
1
1
3
2
9
12
10
11
11-17
3
2
5
????
5
9
10
11
6
4
5
50
Interpretación:
– El número 2 es la frecuencia de la celda correspondiente al par de intervalos 76-79 en Coeficiente
Intelectual y 39-45 en Calificación obtenida en la prueba de conocimiento.
– El número 5 en la fila de ???? es el total marginal o frecuencia marginal del intervalo 76-79 en Coeficiente
Intelectual.
– El número 2 en la columna de ???? es el total marginal o frecuencia marginal del intervalo 53-59 en
Calificación obtenida en la prueba de conocimiento.
– El número 50 es total de frecuencias marginales y representa al número total de estudiantes.

2) Realizando los cálculos respectivos se obtiene la siguiente tabla:

Coeficientes Intelectuales (X)
76-
80-83 84- 88-91 92-
96-
100-103
79
87
95
99
????
-3
-2
-1
0
1
2
3
????
????
????
?? · ????
????
· ????
· ???? 2
· ????
53-59

46-52
3

2
2

1
18

6
2

1
6

2
18

4
18

6
39-45

32-38

25-31

18-24
1

0

-1

-2
2

1

2
-6

3

12
2

2

1

4
-4

0

2

16
1

4

2
0

4

4
1

3

3

2
0

0

0

0
1

3

1

1
1

0

-1

-2
1

3
2

0
2
6
9

12

10

11
9

0

-10

-22
9

0

10

44
-1

0

8

30
11-17
-3
3
9
2
0
5
-15
45
9
????
5
9
10
11
6
4
5
50
-30
130
70
???? · ????
???? · ???? 2
?? · ???? · ????
-15
45
9
-18
36
14
-10
10
17
0
0
0
6
6
-2
8
16
2
15
45
30
-14
158
70
Nota:
Los números de las esquinas de cada celda en la anterior tabla representan el producto
?? · ???? · ????, así por ejemplo, para obtener el número el número -6 de los intervalos 76-79 en X y 39-45 en

9
?? =
=
=
Y se obtiene multiplicando 2·(-3)·1 = -6. Para obtener el número 18 de los intervalos 100-103 en X y 53-
59 en Y se obtiene multiplicando 2·3·3 = 18

Los números de la última columna (18, 6, -1, 0, 8, 30 y 9) se obtienen sumando los números de las
esquinas en cada fila, así por ejemplo, para obtener el número -1 se suma (-6) + (-4) + 0 + 1 +2 + 6 = -1

Los números de la última fila (9, 14, 17, 0, -2, 2 y 30) se obtienen sumando los números de las esquinas
en cada columna, así por ejemplo, para obtener el número 9 se suma (-6) + 3 + 12 = 9.

Para obtener el número -30 de la antepenúlmina columna se obtiene sumando los resultados de ???? · ????,
es decir, representa la ? ???? · ????

Para obtener el número -14 de la antepenúlmina fila se obtiene sumando los resultados de ???? · ????, es
decir, representa la ? ???? · ????

Para obtener el número 130 de la penúltima columna se obtiene sumando los resultados de ???? · ???? 2 , es
decir, representa ? ???? · ????2

Para obtener el número 158 de la penúltima fila se obtiene sumando los resultados de ???? · ????2 , es decir,
representa ? ???? · ????2

Para obtener último número 70 de la última columna se obtiene sumando los resultados de la última
columna 18 +6 +(-1) +0 + 8 + 30 +9 = 70, es decir, representa ? ???? · ???? · ????

Para obtener último número 70 de la última fila se obtiene sumando los resultados de la última fila
+ 14 + 17 + 0 +(-2) +2 + 30 = 70 , es decir, representa ? ???? · ???? · ???? . Por lo tanto tiene que ser igual al
último número de la última columna como comprobación que los cálculos de la tabla han sido correctos.

Observando los datos en la tabla anterior se reemplaza los valores en la ecuación del Coeficiente de
Correlación de Pearson para datos agrupados, obteniéndose:

?? · ? ?? · ???? · ???? – (? ???? · ????) (? ???? · ????)
v[?? · ? ???? · ????2 – (? ???? · ????)2 ][?? · ? ???? · ???? 2 – (? ???? · ????)2 ]
?? =
50 · 70 – (-14)(-30)
v[50 · 158 – (-14)2 ][50 · 130 – (-30)2 ]
3500 – 420
v[7900 – 196][6500 – 900]
3080
v[7704][5600]
?? =
3080
v43142400
=
3080
6568,287448
= 0,469
Existe una correlación positiva moderada

TAREA DE INTERAPRENDIZAJE

1) Elabore un organizador gráfico de los tipos de correlación.

2) Con los datos de la siguiente tabla sobre las temperaturas del día X y del día Y en determinadas horas
en una ciudad

X 9 10 12 14 16 18 20 22 24 26 28 30
Y 12 14 15 16 17 20 22 23 26 28 31 32

2.1) Calcule el coeficiente de correlación de Pearson empleando la fórmula y mediante Excel.
0,99
2.2) Elabore el diagrama de dispersión de manera manual.
2.3) Elabore el diagrama de dispersión empleando Excel.
2.4) Elabore el diagrama de dispersión empleando el programa Graph.

3) Cree y resuelva un ejercicio similar al anterior.

4) Dada la siguiente tabla de frecuencias de dos variables, con los datos sobre las calificaciones obtenidos
en un curso de 50 estudiantes en la asignatura de Matemática (X) y en la asignatura de Estadística (Y),
determinar el tipo de correlación que existe entre ellas mediante el coeficiente de Pearson.
??
1-2 3-4 5-6 7-8 9-10 ????
9-10
7-8
7
6
8
15
6
??
5-6
3-4
5
5
3
1
4
7
11
1-2
7
4
11
????
12
9
4
17
8
50
Correlación positiva muy alta de 0,91

5) Dada la siguiente tabla de frecuencias de dos variables, con los datos sobre los pesos en kilogramos
en dos barrios diferentes en una ciudad, determinar el tipo de correlación que existe entre ellas mediante
el coeficiente de Pearson.
??
40-49 50-59 60-69 70-79 80-89 90-99 ????
90-99
3
3
4
10
80-89
8
2
2
4
16
??
70-79
60-69
8
1
5
2
10
5
8
2
1
24
18
50-59
40-49
3
4
10
6
6
1
2
21
11
????
15
17
22
22
15
9
100
Correlación positiva moderada de 0,688

6) Dada la siguiente tabla de frecuencias de dos variables, con los datos sobre las calificaciones obtenidos
en un curso de 100 estudiantes en la asignatura de Matemática (X) y en la asignatura de Estadística (Y),

7
determinar el tipo de correlación que existe entre ellas mediante el coeficiente de Pearson para datos
agrupados.
N° de
estudiante
X
Y
N° de
estudiante
X Y
N° de
estudiante
X Y
N° de
estudiante
X Y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
40
41
42
43
44
45
45
45
45
48
49
50
50
56
56
56
56
56
57
57
57
57
57
57
57
60
50
55
59
40
42
49
60
62
66
69
50
52
54
56
59
59
40
45
47
48
49
80
70
72
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
57
58
60
61
62
63
64
64
65
65
66
66
66
66
67
68
68
68
69
69
69
69
70
70
70
73
78
79
60
61
62
63
64
65
66
67
69
50
52
55
56
57
59
40
45
47
49
90
99
80
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
71
72
72
72
73
74
74
74
75
76
76
77
77
78
78
78
78
79
79
79
80
81
82
82
83
86
88
89
70
71
72
73
74
75
76
77
78
79
60
67
65
68
69
50
59
90
94
96
99
80
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
84
84
85
86
86
86
87
87
88
88
88
88
89
89
89
90
91
92
93
94
95
96
97
98
99
83
84
86
88
89
70
78
79
78
77
79
78
78
60
69
90
96
97
99
80
81
82
83
89
70
??
??
????
40-48
94-102
????
-3
-2
-1
0
1
2
3
????
94-102 3
2
1
0
-1
-2
5
3
40-48 -3
????
2
10
9
100
Correlación positiva moderada de 0,62
7) Cree y resuelva un ejercicio similar al anterior.

8) Consulte en la biblioteca o en el internet un ejercicio resuelto sobre el coeficiente de correlación de
Pearson para datos agrupados en intervalos.