INTRODUCCION
El árbol binario es una estructura
fundamental en matemática y computación y
también se le aplican algunos de los términos de
los arboles con raíz como arista, camino, hoja,
profundidad y números de nivel. No obstante, en los
arboles binarios se usará el termino nodo, en lugar de
vértice. Debe tener en cuenta que un árbol binario
no es un caso especial de un árbol con raíz; son
entes matemáticos diferentes.
RESUMEN
DEFINICIONES:
Caballero Roldán, Rafael (2007)
afirma: "Un árbol binario es un conjunto finito de
elementos que se denominan nodos"
Veerarajan T. (2008) afirma: "Si todo
vértice interno de todo árbol raíz tiene
exactamente a lo mas 2 hijos, el árbol se denomina
árbol binario completo o árbol binario.
En otras palabras, un árbol binario
completo es aquel en el cual hay exactamente un
vértice(raíz) de grado 2 y cada uno de los
vértices restantes es de grado 1 o 3. "
TIPOS:
– Arboles binarios semejantes: Se
dice que los arboles binarios son semejantes si tiene la misma
estructura o, en otras palabras, si tienen el mismo contenido en
nodos correspondientes.

– Arboles binarios completos: Considere cualquier
árbol binario T. Cada nodo de T puede tener
cuando mucho dos hijos. En consecuencia, es posible demostrar que
el nivel R de T puede tener cuando mucho 2?? nodos.
Se dice que el árbol T es completo si todos
niveles excepto posiblemente el ultimo, tienen el número
máximo de nodos posibles, y si todos los
nodos en el último nivel se encuentran lo más a la
izquierda posible.

– Arboles binarios extendidos
(2-arboles): Se dice que un árbol binario T es un 2-
árbol o un árbol binario extendido ni cada nodo N
tiene 0 o 2 hijos. En tal caso, los nodos con dos hijos se
denominan nodos internos, y los nodos con 0 hijos se denominan
nodos externos. Algunas veces los nodos se distinguen en
diagramas por medio de círculos para los nodos internos y
cuadrados para los nodos externos.

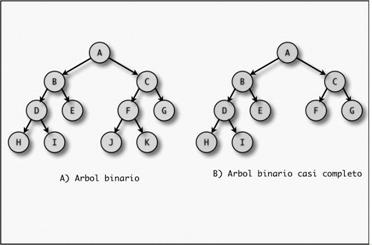
EJEMPLOS DE ARBOLES
BINARIOS:

CONCLUSION
De este trabajo se podría decir que
los arboles binarios son un conjunto finito de elementos llamados
nodos. En estos casos se pude usar terminología de
relaciones familiares para descubrir las relaciones entre los
nodos de un árbol; y que un árbol puede ser
implementado fácilmente en una computadora.
También se puede decir que en este
trabajo encontramos los diferente tipos de árboles
binarios los cuales son muy útiles.
BIBLIOGRAFIA
Caballero Roldán, Rafael (2007).
Matemáticas discretas. Madrid: Person
education
Veerarajan T. (2008).
Matemáticas discretas con teoría de
gráficas y combinatoria.
México: The Mac Graw-Hill
companie
Autor:
Mariela Lourdes Quispe
Vasquez
UNIVERSIDAD NACIONAL DEL
ALTIPLANO
FACULTAD DE INGENIERIA MECANICA ELECTRICA,
ELECTRONICA Y SISTEMAS
ESCUELA PROFESIONAL DE INGENIERIA DE
SISTEMA

7 de enero del 2014