
CENTRODEGRAVEDAD,CENTRODEMASAYCENTROIDE
Ing.JoséLuisAlbornozSalazar
-1-
CENTRO DE GRAVEDAD, CENTRO
DE MASA Y CENTROIDE
El
centro de gravedad
es el punto de aplicación de
la resultante de todas las fuerzas de gravedad que actúan sobre las
distintas porciones materiales de un cuerpo, de tal forma que el
momento respecto a cualquier punto de esta resultante aplicada en el
centro de gravedad es el mismo que el producido por los pesos de todas
las masas materiales que constituyen dicho cuerpo.
En otras palabras, el centro de gravedad de un cuerpo es el punto
respecto al cual las fuerzas que la gravedad ejerce sobre los diferentes
puntos materiales que constituyen el cuerpo producen un momento
resultante nulo.
El centro de gravedad de un cuerpo no corresponde necesariamente a
un punto material del cuerpo. Así, el c.g. de una esfera hueca está
situado en el centro de la esfera que, obviamente, no pertenece al
cuerpo
En física, además del centro de gravedad aparecen los conceptos
de centro de masa y de centro geométrico o centroide que, aunque
pueden coincidir con el centro de gravedad, son conceptualmente
diferentes.
Centro de masa y centro de gravedad: El centro de masas coincide
con el centro de gravedad sólo si el campo gravitatorio es uniforme; es
decir, viene dado en todos los puntos del campo gravitatorio por
un vector de magnitud y dirección constante.
Centro geométrico (Centroide) y centro de masa:
El centro
geométrico de un cuerpo material coincide con el centro de masa si el
objeto es homogéneo (densidad uniforme) o cuando la distribución de
materia en el sistema es simétrico.
En nuestros estudios de Ingeniería Civil se asume que el cuerpo se
encuentra en “condición ideal”, es decir, el campo gravitatorio es
uniforme y el objeto motivo de estudio es homogéneo; luego el centro de
gravedad, el centro de masa y el centroide coinciden en un mismo punto.
Los dos métodos más utilizados para el cálculo del CENTROIDE de
una figura geométrica plana son el Método de las áreas y el Método
de integración directa.
Si una figura geométrica posee un eje de simetría, el centroide de la
figura coincide con este eje.
Para “fijar” las consideraciones anteriores procederemos a resolver
algunos ejercicios.
Método de las áreas :
Ejercicio 1 : Calcular la ubicación del Centroide de la
siguiente figura geométrica.
Solución:
Como primer paso se fija el sistema de coordenadas rectangulares que
nos servirá de referencia:

CENTRODEGRAVEDAD,CENTRODEMASAYCENTROIDE
Ing.JoséLuisAlbornozSalazar
-2-
Posteriormente dividimos la figura en áreas más simples de centroides
conocidos.
Calculamos las áreas de las tres figuras conocidas:
Area A1 (Triángulo) : Base por altura entre dos.
A1 =
Area A2 (Rectángulo) : Base por altura.
A2 = (8)(2) = 16
Area A3 (Rectángulo) : Base por altura.
A3 = (3)(4) = 12
Los ejes centroidales de una figura plana vienen dados por las siguientes
formulas :
Donde “Ai” es el área de la figura simple estudiada, “Xi” es la abscisa del
centroide de dicha figura simple y “Yi” la ordenada del centroide de la
misma figura simple.
Es bueno recordar que el centroide de un triangulo rectángulo está
ubicado a un tercio de su base y a un tercio de su altura.
El centroide de un rectángulo está ubicado a un medio de su base y a un
medio de su altura.
Luego, resulta más cómodo determinar los valores de “X” y “Y” del
centroide de cada una de las figuras simples para incluirlas en la fórmula
respectiva, tomando en cuenta el sistema de coordenadas de referencia.

Ing.JoséLuisAlbornozSalazar
-3-
X2 = 4
Y2 = 1
Estudiando la figura 3 (Rectángulo) :
CENTRODEGRAVEDAD,CENTRODEMASAYCENTROIDE
Estudiando la figura 1 (Triangulo) :
(1 , 3)
X1 = 1
Y1 = 3
Estudiando la figura 2 (Rectángulo) :
(4 , 1)
(6.5 , 4)
X3 = 6,5
Y3 = 4
Con toda esta información el problema se limita a introducir estos valores
en las dos fórmulas:

CENTRODEGRAVEDAD,CENTRODEMASAYCENTROIDE
-4-
El Centroide de la figura completa estará ubicado en :
SUGERENCIA: Divida la figura como se muestra a continuación
y aplique los pasos anteriores. El resultado debe ser el mismo.
Ejercicio 2 : Calcular la ubicación del Centroide de la siguiente
figura geométrica.
Solución:
El área se obtiene con la suma de un rectángulo, un triangulo y un
semicírculo y después se resta un circulo (se sobre entiende que la
figura tiene un hueco en forma de circulo).
Area A1 (Rectángulo) : Base por altura.
A1 = (120)(80) = 9.600 mm2
Area A4 (Circulo) :
A4= p r2 = p (40)2 = 5.026,55 mm2
Ing.JoséLuisAlbornozSalazar
Ing.JoséLuisAlbornozSalazar
-5-
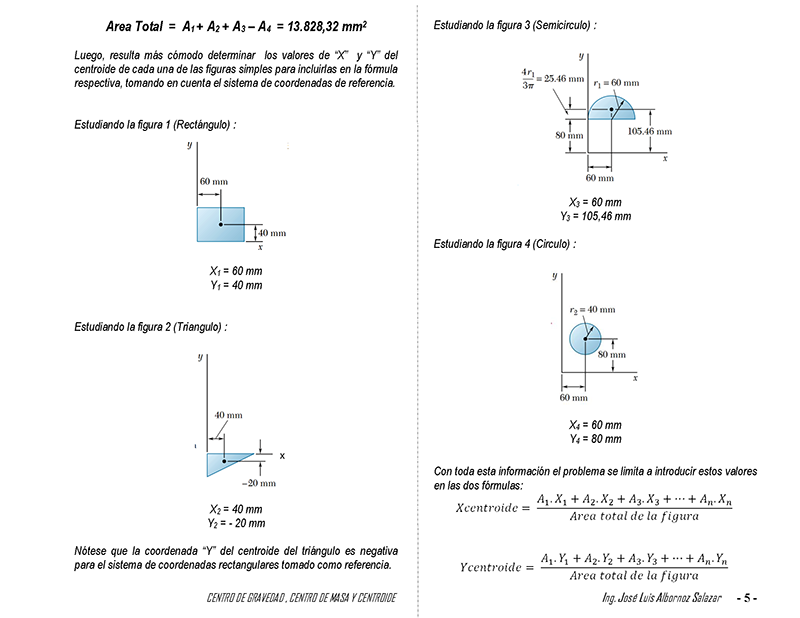
Area Total = A1+ A2 + A3 – A4 = 13.828,32 mm2
Luego, resulta más cómodo determinar los valores de “X” y “Y” del
centroide de cada una de las figuras simples para incluirlas en la fórmula
respectiva, tomando en cuenta el sistema de coordenadas de referencia.
Estudiando la figura 1 (Rectángulo) :
X1 = 60 mm
Y1 = 40 mm
Estudiando la figura 2 (Triangulo) :
X2 = 40 mm
Y2 = – 20 mm
Nótese que la coordenada “Y” del centroide del triángulo es negativa
para el sistema de coordenadas rectangulares tomado como referencia.
CENTRODEGRAVEDAD,CENTRODEMASAYCENTROIDE
Estudiando la figura 3 (Semicirculo) :
X3 = 60 mm
Y3 = 105,46 mm
Estudiando la figura 4 (Circulo) :
X4 = 60 mm
Y4 = 80 mm
Con toda esta información el problema se limita a introducir estos valores
en las dos fórmulas:
x

CENTRODEGRAVEDAD,CENTRODEMASAYCENTROIDE
Ing.JoséLuisAlbornozSalazar
-6-
Debiendo tomar en cuenta que el valor del área del círculo (A4) tendrá
signo negativo y el valor de la coordenada “Y” del centroide del triángulo
(Y2) también tendrá signo negativo
Ycentroide = 36,6 mm
El Centroide de la figura completa estará ubicado en :
Ejercicio 3 : Calcular la ubicación del Centroide de la siguiente
figura geométrica.
Como apuntamos al inicio de esta guía : Si una figura geométrica posee
un eje de simetría, el centroide de la figura coincide con este eje.
Esta figura en particular posee un eje de simetría horizontal y un eje de
simetría vertical, luego su centroide estará ubicado en el punto de
intersección de sus dos ejes de simetría.
Se recomienda que utilice los procedimientos explicados en los dos
ejercicios anteriores y verifique la ubicación del centroide de la figura.

CENTRODEGRAVEDAD,CENTRODEMASAYCENTROIDE
Ing.JoséLuisAlbornozSalazar
-7-
Método de integración directa :
Para calcular el centroide de una figura plana que está limitada por arriba
por la funci{on “f(x)” , por debajo por la función “g(x)”, por la izquierda por
la recta “X = a” y por la derecha por la recta “X = b”; se utilizan las
siguientes fórmulas :
Donde “A” representa el área de la figura plana a la que se le está
calculando el centroide.
Ejercicio 4 : Calcular la ubicación del Centroide de la región
acotada por “Y = X2” y “Y = X”
Solución:
El primer paso consiste en graficar las dos funciones para determinar
cuál queda ubicada arriba y cuál debajo. Igualmente se deben calcular
los puntos de intersección de las dos funciones para conocer los índices
superior e inferior de la integral definida.
Una vez hecha la gráfica podemos decir que :
f(x) = “Y = X”
g(x) = “Y = X2”
a=0
b=1
Calculando el área de la región acotada :

CENTRODEGRAVEDAD,CENTRODEMASAYCENTROIDE
Ing.JoséLuisAlbornozSalazar
-8-
Calculando las coordenadas del centroide :
El centroide estará ubicado en el punto (0.5 , 0.4)
Ejercicio 5 : Calcular la ubicación del Centroide de la región
acotada por “f (x)= 4-x2 “ y “g (x)= x+2” :
Solución:
El primer paso consiste en graficar las dos funciones para determinar
cuál queda ubicada arriba y cuál debajo. Igualmente se deben calcular
los puntos de intersección de las dos funciones para conocer los índices
superior e inferior de la integral definida.
Estas 2 curvas se cortan en (-2,0) y en (1,3), por lo que el área es:

CENTRODEGRAVEDAD,CENTRODEMASAYCENTROIDE
Ing.JoséLuisAlbornozSalazar
-9-
El centroide tiene coordenadas:
El centroide es: (-1/2,12/5)
El centroide es: (-0.5 , 2.4)
Ejercicio 6 : Calcular la ubicación del Centroide de la región
acotada por “Y = X2” y “Y = 8 – X2”
Como apuntamos al inicio de esta guía : Si una figura geométrica posee
un eje de simetría, el centroide de la figura coincide con este eje.
Esta figura en particular posee un eje de simetría horizontal y un eje de
simetría vertical, luego su centroide estará ubicado en el punto de
intersección de sus dos ejes de simetría.
Se recomienda que utilice los procedimientos explicados en los dos
ejercicios anteriores y verifique la ubicación del centroide de la figura.