
13
Gráfica Nº 8: Variación del consumo ante una reducción de s
Oro
A largo plazo la economía convergerá a k t , donde el consumo es superior y
también es superior kt . Entonces si la economía encuentra un kt , entonces
reducimos la tasa de ahorro a un sOro y con esto conseguí aumentar el consumo en
todos los momentos del tiempo.
Entonces podemos concluir que el consumo en el estado proporcionado es máximo
en el estado proporcionado de la regla de oro.
Política de Crecimiento ejercicios resueltos
Problema #1
Suponga que existe una economía capitalista cuya función de producción agregada
t t
es Yt
A.K3/5.L2/5, y se sabe que la tasa de ahorro de esta sociedad es de 30% del
producto agregado cada año, también se sabe que; La tasa de depreciación del
capital es de 8% al año, la tasa de crecimiento de la fuerza de trabajo es del 2% al
año y por ultimo se sabe que el índice de nivel de tecnología es la unidad. Se pide:
a) Hallar la ecuación fundamental de Solow – Swan.
b) Hallar el estado de crecimiento proporcionado.
c) Hallar los valores de capital por trabajador y de producto por trabajador del
estado proporcionado.
d) Hallar la tasa de salario y la tasa de rendimientos bruto del capital y graficar los
valores.
e) Hallar la participación de los salarios y de los beneficios brutos en el ingreso
nacional.
Rpt:
a) Hallar la ecuación fundamental de Solow – Swan.
De los datos tenemos: s
0.30 ,
0.08, n
0.02 A 1

L
Lt Kt
14
t t
Yt
A.K3/5.L2/5, dividiendo la función de producción entre la cantidad de trabajadores
Lt .Lt , donde
(Lt) tenemos:
Para operar con facilidad usaremos un viejo truco matemático Lt
1
t t
K3/5 L2/5
A. 3/5 . 2/5
Lt Lt
Yt
Lt
3/5
(FPI)
A.
A.kt3/5
yt
Kt
Lt
Yt
Lt
Ahora deduciremos la ecuación de Solow – Swan
K t
It
.Kt
(1 s).F(Kt,Lt, A)
Ct
K t
It
Ct
Yt
.Kt
(1 s).F(Kt,.Lt, A)
F(Kt,Lt, A)
K t
1
Lt
.Kt…x
F(Kt, A.Lt)
(I)
.kt
f (kt)
k t
Kt
Lt
kt
2
t
Lt .Kt
K t .Lt
dkt
dt
(II)
k t n.kt
dkt
dt
.
Lt Lt
K t
Lt
k t
Reemplazando la ecuación (I ) en la ecuación (II )
dkt
dt
.kt) n.kt
( f (kt)
(III)
).kt
f (kt) (n
k t
La ecuación (III ) representa la ecuación fundamental de Solow – Swan que hemos
deducido por única vez, solo la mencionaremos y la aplicaremos de forma directa en
las siguientes paginas del libro.
Reemplazado los datos en la ecuación fundamental de Solow – Swan.
k t
(0.30).(1)kt3/5
(0.10)kt , la ecuación de fundamental de Solow – Swan.
b) Hallar el estado de crecimiento proporcionado.
0
0
Para el crecimiento proporcionado tenemos que: k
k t
Dividiendo la ecuación de fundamental de Solow – Swan, entre el capital por
trabajador (kt), tenemos:
0.10
0.30
0.10
(0.30).(1).
1
2/5
t
k
1
2/5
t
k
k
k t
kt
0.10
0.30
0
1
kt2/5
c) Hallar los valores de capital por trabajador y de producto por trabajador del
estado proporcionado.

15
5/ 2
0 . 30
0.10
Despejando, kt, de la ecuación anterior, tenemos kt
15.589
Oro
t
k
Reemplazando, kt, en la función de producción intensiva (FPI)
(15.589)3/5
yt
5.196
yt
sOro.f (kt ) 1.5588
Gráfico del Problema #1
d) Hallar la tasa de salario y de rendimiento bruto de capital y graficar los valores.
Mercado de capital:
2/5
3 1
.
515.589 15.589
d(kt3/5)
dkt
PMgk
r
PMgk
0.1999972
r
Mercado de trabajo:
3
5
1
.A. 2/5 .(kt)
kt
A.kt3/5
W
f (kt).kt
f (kt)
PMgL
W
PMgL
.(1).(15.589)3/5
2
5
2
5
W
W
.A.kt2/5
2.079
W
por trabajador (k ) y un producto por trabajador ( y2 *t ) mayor que el inicial.
16
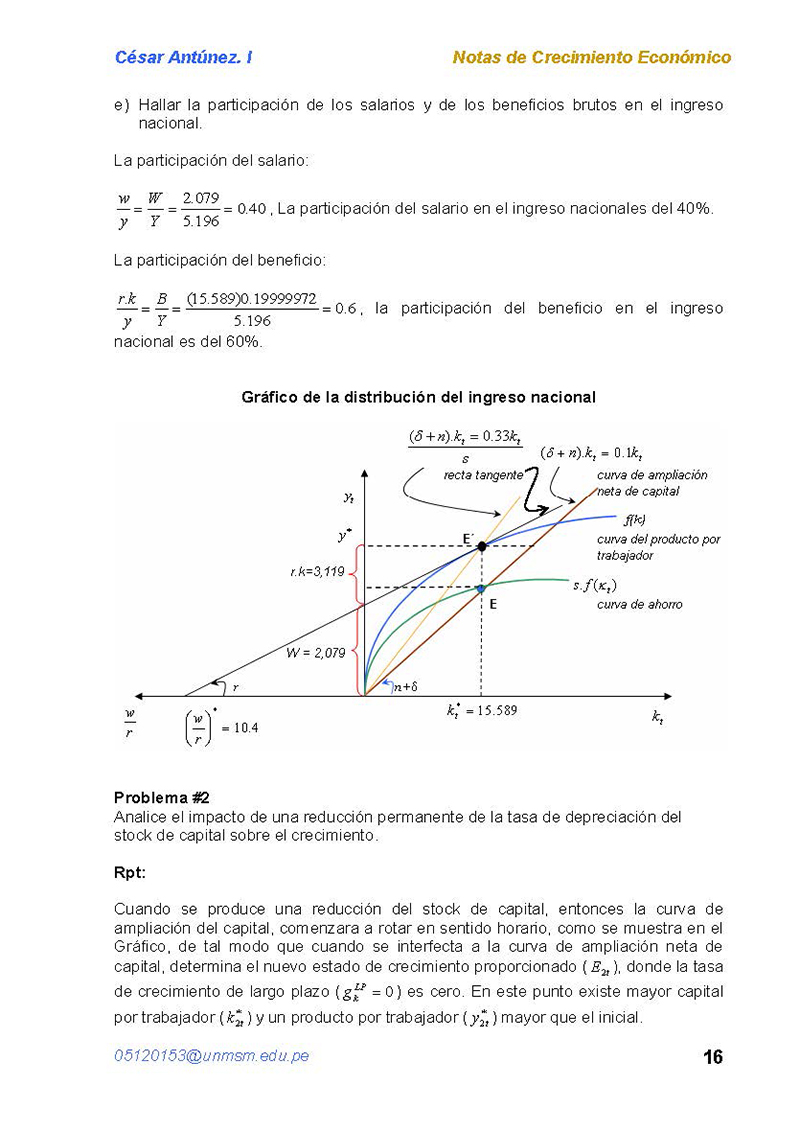
e) Hallar la participación de los salarios y de los beneficios brutos en el ingreso
nacional.
La participación del salario:
2.079
5.196
W
Y
w
y
0.40, La participación del salario en el ingreso nacionales del 40%.
La participación del beneficio:
(15 . 589 ) 0 . 19999972
5.196
B
Y
r.k
y
0.6, la participación del beneficio en el ingreso
nacional es del 60%.
Gráfico de la distribución del ingreso nacional
Problema #2
Analice el impacto de una reducción permanente de la tasa de depreciación del
stock de capital sobre el crecimiento.
Rpt:
Cuando se produce una reducción del stock de capital, entonces la curva de
ampliación del capital, comenzara a rotar en sentido horario, como se muestra en el
Gráfico, de tal modo que cuando se interfecta a la curva de ampliación neta de
capital, determina el nuevo estado de crecimiento proporcionado ( E2t), donde la tasa
k
de crecimiento de largo plazo ( g LP
0) es cero. En este punto existe mayor capital
*
2t
17
*
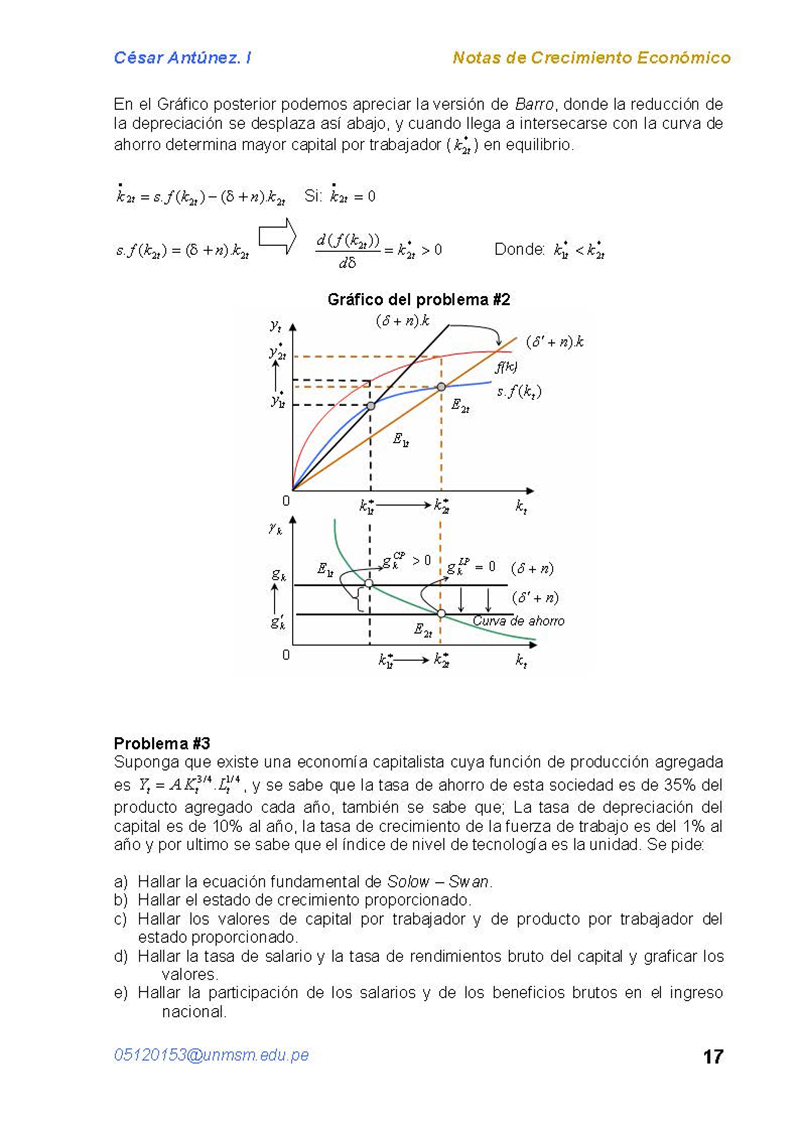
En el Gráfico posterior podemos apreciar la versión de Barro, donde la reducción de
la depreciación se desplaza así abajo, y cuando llega a intersecarse con la curva de
ahorro determina mayor capital por trabajador (k2t) en equilibrio.
k 2t
n).k2t
s.f (k2t) (
0
Si: k 2t
n).k2t
(
s.f (k2t)
0
*
k2t
d( f (k2t))
d
*
*
k2t
Donde: k1t
Gráfico del problema #2
Problema #3
Suponga que existe una economía capitalista cuya función de producción agregada
t t
es Yt
A.K3/4.L 1/4, y se sabe que la tasa de ahorro de esta sociedad es de 35% del
producto agregado cada año, también se sabe que; La tasa de depreciación del
capital es de 10% al año, la tasa de crecimiento de la fuerza de trabajo es del 1% al
año y por ultimo se sabe que el índice de nivel de tecnología es la unidad. Se pide:
a) Hallar la ecuación fundamental de Solow – Swan.
b) Hallar el estado de crecimiento proporcionado.
c) Hallar los valores de capital por trabajador y de producto por trabajador del
estado proporcionado.
d) Hallar la tasa de salario y la tasa de rendimientos bruto del capital y graficar los
valores.
e) Hallar la participación de los salarios y de los beneficios brutos en el ingreso
nacional.

A.Kt .Lt , dividiendo la función de producción entre la cantidad de trabajadores
18
Rpt:
a) Hallar la ecuación fundamental de Solow – Swan.
De los datos tenemos: s
0.35,
0.10, n
0.01 A 1
3/4 1/4
Yt
Lt .Lt , donde
(Lt) tenemos:
Para operar con facilidad usaremos un viejo truco matemático Lt
1
t t
K3/4 L 1/4
A. 3/4 . 1/4
Lt Lt
Yt
Lt
3/4
(FPI)
A.
A.kt3/4
yt
Kt
Lt
Yt
Lt
Reemplazado los datos en la ecuación fundamental de Solow – Swan.
k t
(0.35).(1)kt3/ 4
(0.11)kt , la ecuación de fundamental de Solow – Swan.
b) Hallar el estado de crecimiento proporcionado.
Para el crecimiento proporcionado tenemos que:
0
0
k
k t
Dividiendo la ecuación de fundamental de Solow – Swan, entre el capital por
trabajador (kt), tenemos:
0.11
0.35
0.11
(0.35).(1).
1
1/ 4
t
k
1
1/ 4
t
k
k
k t
kt
0.11
0.35
0
t
1
k1/ 4
c) Hallar los valores de capital por trabajador y de producto por trabajador del
estado proporcionado.
4
0 . 35
0.11
Despejando, kt, de la ecuación anterior, tenemos kt
102.5
t
k
Reemplazando, kt, en la función de producción intensiva (FPI)
(1).(102.5)3/ 4
yt
32.21
yt
s*.f (kt ) 11.27

César Antúnez. I
19
Notas de Crecimiento Económico
Gráfico del Problema #3
d) Hallar la tasa de salario y de rendimiento bruto de capital y graficar los valores.
Mercado de capital:
1/ 4
3 1
.
4 102.5
d(kt3/ 4)
dkt
PMgk
r
PMgk
0.2357112
r
Mercado de trabajo:
3
4
1
.A. 1/ 4 .(kt)
kt
A.kt3/ 4
W
f (kt).kt
f (kt)
PMgL
W
PMgL
.(1).(102.5)3/ 4
1
4
1
4
W
W
.A.kt2/ 4
8.05347
W
e) Hallar la participación de los salarios y de los beneficios brutos en el ingreso
nacional.
La participación del salario:
8 .05347
32.21
W
Y
w
y
0.25, La participación del salario en el ingreso nacionales del
25%.
La participación del beneficio:
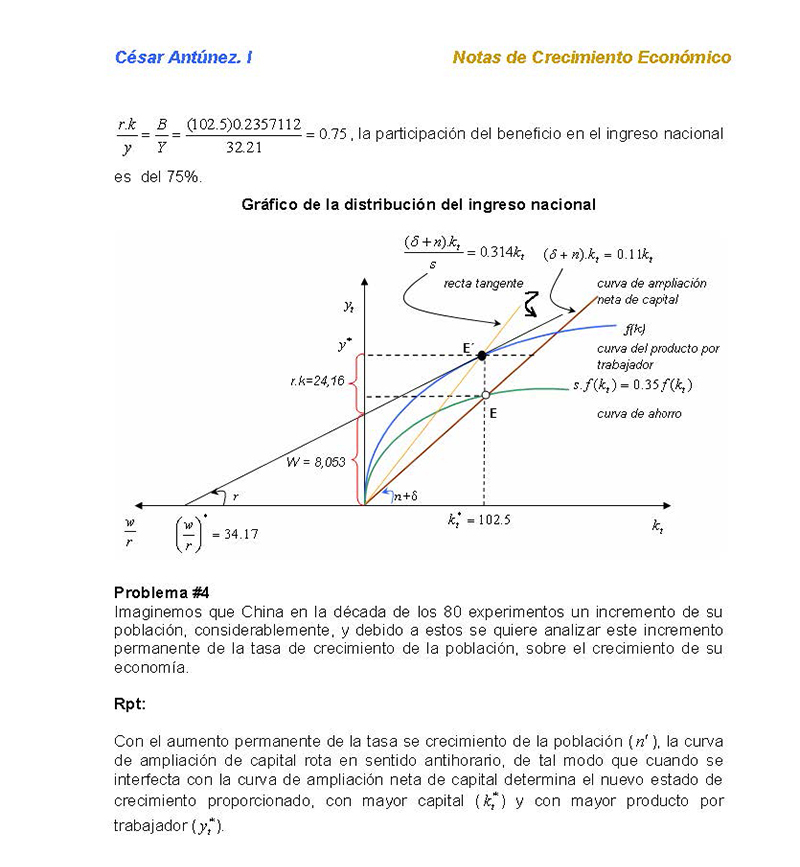
20
(102.5) 0.2357112
32.21
B
Y
r.k
y
0.75, la participación del beneficio en el ingreso nacional
es del 75%.
Gráfico de la distribución del ingreso nacional
t
t
Problema #4
Imaginemos que China en la década de los 80 experimentos un incremento de su
población, considerablemente, y debido a estos se quiere analizar este incremento
permanente de la tasa de crecimiento de la población, sobre el crecimiento de su
economía.
Rpt:
Con el aumento permanente de la tasa se crecimiento de la población (n ), la curva
de ampliación de capital rota en sentido antihorario, de tal modo que cuando se
interfecta con la curva de ampliación neta de capital determina el nuevo estado de
crecimiento proporcionado, con mayor capital (k *) y con mayor producto por
trabajador ( y*).

César Antúnez. I
21
Notas de Crecimiento Económico
Gráfico del problema #4
En la versión de Barro que se muestra en la parte inferior de nuestro Gráfico
presentado, podemos apreciar, que el aumento de la tasa de crecimiento de la
población hace que la curva de depreciación se desplace así arriba y al intersecarse
con la curva de ahorro genere el nuevo punto de equilibrio ( E2t). En este punto
existe un menor capital por trabajador.
Nótese que este mismo aumento de la tasa de crecimiento potencial de la economía.
n tasa _ progreso _tecnológico
gPotencial _ LP
gPotencial
Si n
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |