=
ES NECESARIO ASEGURARSE CONTRA CHOQUES
Un automóvil de 1800 kg. Detenido en un semáforo es golpeado por atrás por un auto de 900 kg.
Y los dos quedan enganchados. Si el carro mas pequeño se movía 20 m/seg antes del choque.
Cual es la velocidad de la masa enganchada después de este???.
El momento total del sistema (los dos autos) antes del choque es igual al momento total del
sistema después del choque debido a que el momento se conserva en cualquier tipo de choque.
ANTES DEL CHOQUE
m1 = masa del automóvil que esta detenido = 1800 kg.
V1i = Velocidad del automóvil que esta detenido = 0 m/seg.
m2 = masa del automóvil que golpea = 900 kg.
V2i = Velocidad del automóvil que golpea = 20 m/seg.
DESPUES DEL CHOQUE
mT = (m1 + m2) = 1800 + 900 = 2700 kg. Por que los autos después del choque quedan unidos
VF = Velocidad con la cual se desplazan los dos autos unidos después del choque.
0
m1 * V1i
+ m2 * V2i = mT VF
m2
* V2i = mT VF
VF =
m 2 * V2i 900 * 20 180
m T 2700 27
= 6,66
m
seg
VF = 6,66 m/seg.
Debido a que la velocidad final es positiva, la dirección de la velocidad final es la misma que la
velocidad del auto inicialmente en movimiento.
Que pasaría si ???
Suponga que invertimos las masas de los autos. Un auto estacionario de 900 kg. Es golpeado
por un auto de 1800 kg. En movimiento. ¿Es igual la rapidez final que antes.
Intuitivamente podemos calcular que la rapidez final será mas alta con base en experiencias
comunes al conducir autos. Matemáticamente, este debe ser el caso , por que el sistema tiene
una cantidad de movimiento mayor si el auto inicialmente en movimiento es el mas pesado. Al
despejar la nueva velocidad final , encontramos que:
ANTES DEL CHOQUE
m1 = masa del automóvil que esta detenido = 900 kg.
V1i = Velocidad del automóvil que esta detenido = 0 m/seg.
m2 = masa del automóvil que golpea = 1800 kg.
V2i = Velocidad del automóvil que golpea = 20 m/seg.
DESPUES DEL CHOQUE
mT = (m1 + m2) = 1800 + 900 = 2700 kg. Por que los autos después del choque quedan unidos
VF = Velocidad con la cual se desplazan los dos autos unidos después del choque.
6

=
=
2
1
2
0
m1 * V1i
+ m2 * V2i = mT VF
m2
* V2i = mT VF
VF =
m 2 * V2i 1800 * 20 36000
m T 2700 2700
= 13,33
m
seg
VF = 13,33 m/seg.
QUE ES EN VERDAD MAS ALTA QUE LA VELOCIDAD FINAL PREVIA.
EL PENDULO BALISTICO
El péndulo balístico (Fig. 9.11) es un sistema con el que se mide la velocidad de un proyectil que
se mueve con rapidez, como una bala.
La bala se dispara hacia un gran bloque de madera suspendido de algunos alambres ligeros. La
bala es detenida por el bloque y todo el sistema se balancea hasta alcanzar la altura h. Puesto
que el choque es perfectamente inelástico y el momento se conserva, la ecuación 9.14
proporciona la velocidad del sistema inmediatamente después del choque cuando suponemos la
aproximación del impulso. La energía cinética un momento después del choque es:
K =
(m1 + m 2 ) VF
(ECUACION 1)
ANTES DEL CHOQUE
m1 = Masa de la bala
V1i = Velocidad de la bala antes del choque
m2 = masa del bloque de madera.
V2i = Velocidad del bloque de madera = 0
DESPUES DEL CHOQUE
(m1 + m2) kg.
Por que la bala se incrusta en el bloque de madera después del choque.
VF = Velocidad con la cual se desplaza el conjunto bloque de madera + la bala.
7

m * V1i 2
m1 + m 2
2 1 (m V )2
(m1 + m2 )2
1
2
=
0
m1 * V1i
+ m2 * V2i = mT VF
m1
* V1i = mT VF
VF =
m1 * V1i
m1 + m 2
Elevando al cuadrado ambas expresiones
(VF ) 2 = ( 1 )
(ECUACION 2)
Reemplazando la ecuación 2 en la ecuación 1 tenemos:
K =
1
2
(m1 + m 2 ) VF = 2 (m1 + m 2 ) 1 1i
Cancelando (m1
+ m2)
K =
K =
1
2
1
2
(m1 V1i )2
(m1 + m2 )
(m1 )2 ( V1i )2
(m1 + m2 )
Donde
V1i = Velocidad de la bala antes del choque
K es la energía cinética un momento después del choque.
Sin embargo, en todos los cambios de energía que ocurren después del choque, la energía es
constante.
La energía cinética en el punto mas bajo se transforma en energía potencial cuando alcance la
altura h.
Energía cinética en el punto mas bajo = Energía potencial cuando alcance la altura h.
(m1 )2 ( V1i )2
(m1 + m2 )
= (m1 + m 2 ) g h
(m1 )2 (V1i )2
(m1 )2 (V1i )2
= 2 (m1 + m 2 ) (m1 + m 2 ) g h
= 2 (m1 + m 2 )2 g h
(V1i )2
2 (m1 + m 2 )2 g h
(m1 )2
8

(0,005 + 1)
V1i =
2 (m1 + m 2 )2 g h
(m1 )2
V1i =
(m1
+ m 2 )
m1
2 g h
Ejercicio: En un experimento de péndulo balistico suponga que h = 5 cm = 0,05 metros
m1 = Masa de la bala = 5 gr. = 0,005 kg.
m2 = masa del bloque de madera = 1 kg.
Encuentre:
a) La velocidad inicial del proyectil? V1i = Velocidad de la bala antes del choque
b) La perdida de energía por el choque.
V1i =
(m1
+ m 2 )
m1
2 g h
V1i =
V1i =
V1i =
2 * 9,8 * 0,05
0,005
( 1,005) 0,98
0,005
( 1,005) * 0,9899 = 0,9948 = 198,96 m
0,005 0,005 seg
V1i = Velocidad de la bala antes del choque = 198,96 m/seg.
UN CHOQUE DE DOS CUERPOS CON UN RESORTE
Un bloque de masa m1 = 1,6 kg. Que se mueve inicialmente hacia la derecha con una velocidad
de 4 m/seg. Sobre una pista horizontal sin fricción choca con un resorte unido a un segundo
bloque de masa m2 = 2,1 kg. Que se mueve hacia la izquierda con una velocidad de 2,5 m/seg.
Como muestra la figura 9.12a. El resorte tiene una constante de resorte de 600 N/m.
a) En el instante en el que m1 se mueve hacia la derecha con una velocidad de 3 m/seg como
en la figura 9.12b determine la velocidad de m2
9

1 1 1
2f 2
2
2
1
2
1
2
2
2
22
ANTES DEL CHOQUE
m1 = Masa del bloque = 1,6 kg.
V1i = Velocidad del bloque hacia la derecha = 4i m/seg.
m2 = masa del bloque que esta unido al resorte = 2,1 kg.
V2i = Velocidad del bloque que esta unido al resorte = – 2,5 i m/seg
DESPUES DEL CHOQUE
V1f = Velocidad del bloque m1 hacia la derecha después del choque = 3i m/seg.
V2f = Velocidad del bloque m2 después del choque.
Advierta que la velocidad inicial de m2 es – 2,5i m/seg. Por que su dirección es hacia la
izquierda.
Puesto que momento total se conserva, tenemos:
m1 * V1i
+ m2 * V2i =
m1 * V1f
+ m2 * V2f
(1,6) * (4) + (2,1) * (- 2,5) = (1,6) * (3) + (2,1) * V2f
6,4 – 5,25
= 4,8 + 2,1 V2f
1,15
= 4,8 + 2,1 V2f
1,15 – 4,8 = 2,1 V2f
– 3,65 = 2,1 V2f
V2f =
– 3,65
2,1
= – 1,738
m
seg
El valor negativo de V2f significa que m2 aun se mueve hacia la izquierda en el instante que
estudiamos.
b) Determine la distancia que el resorte se comprime en ese instante???
Para determinar la compresión del resorte X usamos la conservación de la energía, puesto que
no hay fricción ni otras fuerzas no conservativas que actúen sobre el sistema.
m1 V1i +
m 2 V2i = m1 V1f + m 2 V 2 + K X 2
Cancelando ½ en toda la expresión
m1 V1i + m 2 V2i = m1 V1f + m 2 V2f + K X 2
m1 = Masa del bloque = 1,6 kg.
V1i = Velocidad del bloque hacia la derecha = 4i m/seg.
m2 = masa del bloque que esta unido al resorte = 2,1 kg.
V2i = Velocidad del bloque que esta unido al resorte = – 2,5 i m/seg
V1f = Velocidad del bloque m1 hacia la derecha después del choque = 3i m/seg.
V2f = Velocidad del bloque m2 después del choque. = – 1,738 m/seg.
K = constante del resorte = 600 N/m
10

1 1 1
2f 2
2
2
1
2
1
2
2
2
2 2
1,6 * (4) 2 + 2,1 * (- 2,5)2
1,6 * (16) + 2,1 * (6,25)
= 1,6 * (3)2 + 2,1 * (- 1,738)2 + 600 * X 2
= 1,6 * (9) + 2,1 * (3) + 600 X 2
25,6 + 13,12 = 14,4 + 6,3 + 600 X2
38,72 = 20,7 + 600 X2
38,72 – 20,7 = 600 X2
18 = 600 X2
X 2 =
18
600
X =
18
600
= 0,03
X = 0,173 metros
Determine la velocidad de m1 y la compresión en el resorte en el instante en que m2 esta en
reposo.
m1 = Masa del bloque = 1,6 kg.
V1i = Velocidad del bloque hacia la derecha = 4i m/seg.
m2 = masa del bloque que esta unido al resorte = 2,1 kg.
V2i = Velocidad del bloque que esta unido al resorte = – 2,5 i m/seg
V1f = Velocidad del bloque m1 hacia la derecha después del choque = 3i m/seg.
V2f = 0
0
m1 * V1i
+ m2 * V2i =
m1 * V1f
+ m2 * V2f
(1,6) * (4) + (2,1) * (- 2,5) = (1,6) * V1f
6,4 – 5,25
= 1,6 V1f
1,15
= 1,6 V1f
V1f =
1,15
1,6
= 0,71
m
seg
V1f = Velocidad del bloque m1 hacia la derecha después del choque = 0,71 m/seg.
m1 V1i +
m 2 V2i = m1 V1f + m 2 V 2 + K X 2
Cancelando ½ en toda la expresión
m1 V1i + m 2 V2i = m1 V1f + m 2 V2f + K X 2
11

?
PERO. V2f = 0
1,6 * (4) 2 + 2,1 * (- 2,5)2
= 1,6 * (0,71)2
+ 600 * X 2
1,6 * (16) + 2,1 * (6,25)
= 1,6 * (0,5041) + 600 X 2
25,6 + 13,12 = 0,8 + 600 X2
38,72 = 0,8 + 600 X2
38,72 – 0,8 = 600 X2
37,92 = 600 X2
X 2 =
37,92
600
= 0,0632
X = 0,251 metros
COLISIONES EN DOS DIMENSIONES
Un auto de 1500 kg que viaja hacia el este con rapidez de 25 m/seg choca en un crucero con
una camioneta de 2500 kg que viaja al norte a una rapidez de 20 m/seg. Como se muestra en la
figura 9.14. Encuentre la dirección y magnitud de la velocidad de los vehículos chocados
después de la colisión, suponiendo que los vehículos experimentan una colisión perfectamente
inelástica (esto es se quedan pegados).
VF
VFY
m1 = 1500 kg
V1 = 25 m/seg
m2 = 2500 kg
VFX = VF cos ?
V2 = 20 m/seg
PiX : Cantidad de movimiento en el eje X antes del choque
PFX : Cantidad de movimiento en el eje X después del choque
PiY : Cantidad de movimiento en el eje Y antes del choque
PFY : Cantidad de movimiento en el eje Y después del choque
PXi
PYi
= tg ?
Movimiento en el eje X antes del choque.
PiX : Cantidad de movimiento en el eje X antes del choque = m1 * V1
m1 = 150 kg.
V1 = 25 m/seg
12

PiX = m1 * V1 = 1500 * 25 = 37500 kg * m/seg
PiX = 37500 Ecuación 1
Movimiento en el eje X después del choque.
Como la colisión es inelástica, quiere decir que los carros quedan unidos después del choque.
VFX : Es la velocidad final en el eje x de los dos carros después del choque.
VFX = VF cos ? (Ver grafica)
m1 = 1500 kg. m2 = 2500 kg.
PFX : Cantidad de movimiento en el eje X después del choque = (m1 + m2) * VFX
PFX = (m1 + m2) * VFX
PFX = (m1 + m2) * VF cos ?
PFX = (1500 + 2500) * VF cos ?
PFX = (4000) * VF cos ?
Ecuación 2
Igualando la Ecuación 1 y la Ecuación 2 (La cantidad total de movimiento en la direccion del eje
X se conserva podemos igualar las ecuaciones).
PiX = 37500
PFX = (4000) * VF cos ?
37500 = (4000) * VF cos ?
Ecuación 3
Movimiento en el eje Y antes del choque.
PiY : Cantidad de movimiento en el eje Y antes del choque = m2 * V2
m2 = 2500 kg.
V2 = 20 m/seg
PiY = m2 * V2 = 2500 * 20 = 50000
PiY = 50000 Ecuación 4
Movimiento en el eje Y después del choque.
Como la colisión es inelástica, quiere decir que los jugadores quedan unidos después del
choque.
VFY : Es la velocidad final en el eje Y de los dos jugadores después del choque.
VFY = VF sen ? (Ver grafica)
m1 = 1500 kg. m2 = 2500 kg.
PFY : Cantidad de movimiento en el eje Y después del choque = (m1 + m2) * VFY
PFY = (m1 + m2) * VFY
PFY = (m1 + m2) * VF sen ?
PFy = (1500 + 2500) * VF sen ?
PFY = (4000) * VF sen ?
Ecuación 5
Igualando la Ecuación 4 y la Ecuación 5 (La cantidad de movimiento se conserva antes y
después del choque).
PiY = 50000
PFY = (4000) * VF sen ?
50000 = (4000) * VF sen ? Ecuación 6
Dividiendo Ecuación 6 con la Ecuación 3
13

=
=
I =
I
50000 4000 VF sen ?
37500 4000 VF cos ?
Cancelando términos semejantes.
50000
37500
=
sen ?
cos ?
= tg?
1,333 = tg ?
? = arc tg 1,333
? = 53,1 0
Reemplazando en la Ecuación 3, para hallar la velocidad final
37500 = (4000) * VF cos ?
Ecuación 3
VF =
37500 37500
4000 cos (53,1) 2401,68
=
VF = 15,61 m/seg.
Problema 1. Cuarta edición Serway; Problema 1. Quinta edición Serway; Problema 1. Sexta
edición Serway
Una partícula de 3 kg tiene una velocidad de (3i – 4j) m/s. Encuentre sus componentes de
momento X, Y y la magnitud de su momento total.
v = (3i – 4j)
m = 3 kg.
I = Impulso = m * v
I = Impulso = 3 kg. * (3i – 4j) m/seg.
I = (9i – 12j) kg. m/seg.
IX = 9 kg. m/seg.
IY = -12 kg. m/seg.
I =
(I X )2 + (I Y )2
(9)2 + (- 12)2
I = 15 kg. m/seg.
= 81 + 144 = 225
tg ? = Y =
I X
– 12
9
= – 1,333
T = arc tg (- 1,333)
T = – 530
Problema 2 Cuarta edición Serway
Una bola de boliche de 7 kg se mueve en línea recta a 3 m/s. ¿Qué tan rápido debe moverse una
bola de ping-pong de 2.45 gr. en una línea recta de manera que las dos bolas tengan el mismo
momento?
mB = masa del boliche = 7 kg.
VB = Velocidad del boliche = 3 m/seg.
14

=
=
=
mp = masa de la bola de ping pong = 2,45 gr. = 0,00245 kg.
VP = Velocidad de la bola de ping pong
Cantidad de movimiento de la bola de boliche = Cantidad de movimiento de la bola de ping pong
mB * VB = mp * VP
VP =
m B * VB
m p
7 * 3 21
0,00245 0,00245
= 8571,42
m
seg.
VP = Velocidad de la bola de ping pong = 8571,42 m/seg.
Problema 2 Quinta edición Serway; Problema 2 Sexta edición Serway;
Se lanza una bola de 0,1 Kg. en línea recta hacia arriba en el aire con rapidez inicial de 15
m/seg. Encuentren el momentum de la bola.
a) En su máxima altura.
b) A la mitad de su camino hacia el punto máximo.
a) En su máxima altura.
Cuando la bola alcanza su máxima altura, la velocidad es cero, por lo tanto la cantidad de
movimiento también es cero.
b) A la mitad de su camino hacia el punto máximo.
V1 = Velocidad inicial de la bola = 15 m/seg.
V2 = Velocidad final a la máxima altura = 0
V3 = Velocidad cuando la bola este en el punto medio.
Hallamos la máxima altura
(V2)2 = (V1)2 – 2 g h (El signo es negativo por que la bola va perdiendo velocidad hasta que sea
cero).
0 = (V1)2 – 2 g h
(V1)2 = 2 g h
h =
(V1 )2
2 g
=
(15)2
2 * 9,8
=
225
19,6
= 11,47 metros
Hallamos la altura en el punto medio
h 11,47
2 2
= 5,73 metros
Con la altura media, se puede hallar la velocidad en ese punto.
V3 = Velocidad cuando la bola este en el punto medio.
(V3)2 = (V1)2 – 2 g h
(El signo es negativo por que la bola va perdiendo velocidad hasta que sea
cero).
(V3)2 = (15)2 – 2 * 9,8 * 5,73
(V3)2 = 225 – 112,5
(V3)2 = 112,5 m/seg.
v 3 = 112,5
15

V3 = 10,6 m/seg.
Cantidad de movimiento en el punto medio = m1 * V3
Cantidad de movimiento en el punto medio = 0,1 kg. * 10,6 m/seg.
Cantidad de movimiento en el punto medio = 1,06 Kg. – m/seg.
Problema 3 Cuarta edición Serway.
Un niño bota una gran pelota sobre una acera. El impulso lineal entregado por la acera a la
pelota es 2 N-seg. durante 1/800 seg. de contacto.
¿Cuál es la magnitud de la fuerza promedio ejercida por la acera sobre la pelota?
I = Impulso = F * t = 2 Newton . seg.
F =
I
t
=
2
1
= 1600 Newton
800
Problema 3 Quinta edición Serway
Un niño de 40 kg. parado sobre un lago helado arroja una piedra de 0,5 kg. hacia el este con
rapidez de 5 m/seg. Despreciando la fricción entre el niño y el hielo, encuentre la velocidad de
retroceso del hielo?
(+) hacia el este.
mn = masa del niño = 40 Kg.
V = Velocidad de retroceso del hielo
mp = masa de la piedra = 0,5 Kg.
Vp = Velocidad de la piedra = 5 m/seg.
mn * V = – mp * Vp
40 * V = – 0,5 * 5
40 V = – 2,5
V =
– 2,5
40
= – 0,0625
m
seg.
Problema 4 Cuarta edición Serway.
Una gran pelota con una masa de 60 g se deja caer desde una altura de 2 m. Rebota hasta una
altura de 1.8 m. ¿Cuál es el cambio en su momento lineal durante el choque con el piso?
m = 60 gr. = 0,06 kg.
Via = Velocidad inicial antes = o
VFa = Velocidad final antes
h1 = altura que se deja caer la pelota. = 2 m
Vid = Velocidad inicial después
VFd = Velocidad final después = 0
h1 = 2 m
h2 = 1,8 m
h2 = altura que rebota la pelota. = 1,8 m
Se halla la velocidad con la cual la pelota choca en el suelo.
(VFa)2 = (Via)2 + 2 g h1
16

4,5
Vp = = 31,03
(VFa)2 = 0 + 2 g h1
VFa =
2 * 9,8 * 2 = 39,2 = 6,2609
m
seg
VFa = – 6,2609 m/seg Se asume (-) cuando el cuerpo se desplaza hacia abajo.
Se halla la velocidad con la cual la pelota rebota en el suelo.
(VFd)2 = (Vid)2 + 2 g h2
0 = (Vid)2 * 2 g h2
Vid =
2 * 9,8 *1,8 = 35,28 = 5,9396
m
seg
Se asume (+) cuando el cuerpo se desplaza hacia abajo.
? P = PF – Pi = m VF – mVi
? P = (0,06 * 5,9396) – (0,06 * (- 6,2609))
? P = (0,3563) – (- 0,3756)
? P = 0,3563 + 0,3756
? P = 0,731 kg * m/seg.
Problema 4 Quinta edición Serway.
Un pitcher dice que puede lanzar una pelota de béisbol con tanto momentum como una bala de 3
gr. moviéndose con una rapidez de 1500 m/seg. Una pelota de béisbol tiene una masa de 0,145
kg. Cual debe ser su rapidez, si la declaración del pitcher es valida?
mb = masa de la bala = 3 gr. = 0,003 Kg.
Vb = Velocidad de la bala = 1500 m/seg.
mp = masa de la pelota de béisbol = 0,145 kg.
Vp = Velocidad de la pelota de béisbol
Cantidad movimiento de la pelota de béisbol = cantidad de movimiento de la bala
mp * Vp = mb * Vb
0,145 * Vp = 0,003 * 1500
0,145 Vp = 4,5
0,145
m
seg.
Problema 5 Cuarta edición Serway.
La fuerza FX que actúa sobre una partícula de 2 kg varía en el tiempo, como se muestra en la
figura P9.5. Encuentre a) el impulso de la fuerza,
b) la velocidad final de la partícula si inicialmente está en reposo,
c) su velocidad final si al principio se mueve a lo largo del eje x con una velocidad de -2 m/s, y
d) la fuerza promedio ejercida sobre la partícula en el espacio de tiempo ti = 0 a tF = 5 seg.
El área bajo la curva es el impulso.
t =5
I = ? F dt
t =0
17

1
1
2
=
*
*
Pero por geometría se pueden hallar las tres áreas y se suman, esto equivale a encontrar el
impulso.
Area 1 = * 2 * 4 = 4 Newnton. seg
2
Area 2 = 1 * 4 = 4 Newton . seg.
Area 3 =
* 2 * 4 = 4 Newnton. seg
I = area 1 +area 2 + area 3
I = 4 +4 +4 = 12 Newton . seg.
b) la velocidad final de la partícula si inicialmente está en reposo, es decir V0 = 0
m = 2 kg.
I = m * (VF – V0)
I = m * VF
12 = 2 * VF
VF = 6 m/seg.
c) su velocidad final si al principio se mueve a lo largo del eje x con una velocidad de V0 = -2 m/s,
y
VF = V0 + 6 m/seg.
VF = – 2 + 6 m/seg.
VF = 4 m/seg.
d) la fuerza promedio ejercida sobre la partícula en el espacio de tiempo ti = 0 a tF = 5 seg.
Impulso = Fuerza * tiempo
Impulso = 12 Newton . seg.
tiempo = 5 seg (Ver grafica)
Fuerza promedio =
I 12
t 5
= 2,4 Newton
Problema 6 Sexta edición Serway;
Un amigo dice que, mientras tenga puesto su cinturón de seguridad, puede sujetar un niño de 12
kg. En un choque de frente a 60 millas/hora. Con un muro de ladrillo en el que el compartimiento
de pasajeros del auto se detiene en 0,05 seg. Demuestre que la violenta fuerza durante el
choque va a arrebatar al niño de los brazos del amigo. Un niño siempre debe estar en una silla
para niño asegurada con un cinturón de seguridad en el asiento trasero del vehiculo.
F (? t) = ? P = PF – Pi = m VF – mVi
Vi = 60
millas 1609 metros
hora 1 milla
1 hora
3600 seg.
= 26,81
m
seg
Fuerza promedio =
? P = m(VF – Vi ) = 12 [0 – 26,81] = – 321,8
? t ? t 0,05 0,05
Newton
F = – 6436 Newton
18

1
1 ? P 2
?
?
?
?
?
?
?
K = ?
?
?
?
1
En el choque, la fuerza desarrollada es de 6436 newton, lo cual es imposible que el amigo pueda
sostener el niño en los brazos cuando ocurre el choque.
Problema 7 quinta edición Serway; Problema 5 Sexta edición Serway.
a) Una partícula de masa m se mueve con momentum P.
Muestre que la energía cinética de la partícula esta dada por:
K =
P 2
2 m
b) Exprese la magnitud del momentum de la partícula en términos de su energía cinética y masa.
K = Energía cinética
P = Momentum = m v
v =
P
m
v 2 =
P 2
m 2 (Ecuación 1)
K = m v 2
2
(Ecuación 2)
Reemplazando la (Ecuación 1) en la (Ecuación 2)
K =
1
2
m v 2 = m ?
2 ? m 2
?
?
Simplificando m
K =
1
2
? P 2
? m
?
?
? P 2 ?
? 2m ?
b) Exprese la magnitud del momentum de la partícula en términos de su energía cinética y
masa.
K = m v 2
2
2 K = m v2
v 2 =
v =
2 K
m
2 K
m
P = Momentum = m v
P = m
2 K
m
P = m
2 K
m
=
2 K m 2
m
Simplificando la masa m
19

P =
2 K m
Problema 8 Serway cuatro.
Una pelota de 0,15 kg. De masa se deja caer del reposo, desde una altura de 1,25 metros.
Rebota del piso para alcanzar una altura de 0,96 metros. Que impulso dio el piso a la pelota.
m = 0,15 kg.
Via = Velocidad inicial antes = o
VFa = Velocidad final antes
h1 = altura que se deja caer la pelota.
Vid = Velocidad inicial después
VFd = Velocidad final después = 0
h1 = 1,25 m
h2 = 0,96 m
h2 = altura que rebota la pelota.
Se halla la velocidad con la cual la pelota choca en el suelo.
(VFa)2 = (Via)2 + 2 g h1
(VFa)2 = 0 + 2 g h1
VFa =
2 * 9,8 *1,25 = 24,5 = 4,9497
m
seg
VFa = – 4,9497 m/seg Se asume (-) cuando el cuerpo se desplaza hacia abajo.
Se halla la velocidad con la cual la pelota rebota en el suelo.
(VFd)2 = (Vid)2 + 2 g h2
0 = (Vid)2 * 2 g h2
Vid =
2 * 9,8 * 0,96 = 18,816 = 4,3377
m
seg
Se asume (+) cuando el cuerpo se desplaza hacia abajo.
? P = PF – Pi = m VF – mVi
? P = (0,15 * 4,3377) – (0,15 * (- 4,9497))
? P = (0,6506) – (- 0,7424)
? P = 0,6506 + 0,7424
? P = 1,393 kg * m/seg.
Problema 9 Serway cuatro.
Una ametralladora dispara balas de 35 gr. a una velocidad de 750 m/s. Si el arma puede disparar
200 balas/min, ¿cuál es la fuerza promedio que el tirador debe ejercer para evitar que la
ametralladora se mueva?
? P = PF – Pi = m VF – mVi
Pero Pi = 0
? P = PF = m VF = I
20

=
F =
? 1 ?
? 2
?
? 1 ?
? 2
?
? 1
( 3 V )2 ???
? 2
m = 35 gr = 0,035 kg
I = m VF
I = 0,035 kg * 750 m/seg
I = 26,25 kg m/seg
(es el impulso debido a una sola bala, no se olvide que el arma lanza un total de 200 balas
en un tiempo de 60 seg)
Se considera un tiempo de disparo de 60 seg. por que esa es la cantidad de tiempo que dispara
el arma las balas, además la cantidad de balas disparada por la masa de cada bala es la masa
total de balas disparadas en la unidad de tiempo.
I= Ft
26,25 * 200 = F * 60 seg
Despejando la fuerza
26,25 * 200 5250
60 60
= 87,5 Newton
F = 87,5 Newton
Problema 10 Serway cuatro.
a) Si el momento de un objeto se duplica en magnitud. Que ocurre con su energía cinética?
b) Si la energía cinética de un objeto se triplica, que sucede con su momento?
Si el momento de un objeto se duplica en magnitud. Que ocurre con su energía cinética?
P=mV
Observamos por la Ecuación de momento, que si el momento se dobla es por que la velocidad
se dobla.
2P = m (2V)
Por lo tanto, si la velocidad se dobla la energía cinética se aumenta cuatro veces.
K =
1
2
m v 2
K =
1
2
m (2V )2
K = [4] ? m (V )2 ?
Si la energía cinética de un objeto se triplica, que sucede con su momento?
K =
1
2
m v 2
K = [3] ? m ( V )2 ?
K = ? m
Para que la energía cinética se aumente 3 veces es necesario la V se aumente raíz de 3 veces la
velocidad.
21

F = =
=
I
m
Problema 11 Serway cuatro.
Un balón de fútbol de 0.5 kg se lanza con una velocidad de 15 m/s. Un receptor estacionario
atrapa la pelota y la detiene en 0.02 seg.
a) ¿Cuál es el impulso dado al balón?
b) ¿Cuál es la fuerza promedio ejercida sobre el receptor?
Mb = 0,15 kg. masa del balón de fútbol
Vf = 0 m/seg. Velocidad final del balón
Vi = 15 m/seg. Velocidad inicial que se le imprime al balón
?P = m VF – m Vi
?P = 0,15 * (0) – 0,15 * (15)
?P = 0 – 7,5
?P = – 7,5 kg * m/seg. = I
I = F * t = – 7,5 Newton * seg
I – 7,5 Newton * seg 750
t 0,02 seg 2
= – 375 kg *
m
seg 2
F = – 375 newton
Problema 12 Serway CUARTA edición Problema 8 Serway quinta edición;
Un auto se detiene frente a un semáforo. Cuando la luz vuelve al verde el auto se acelera,
aumentando su rapidez de cero a 5,2 m/seg. en 0,832 seg.
Que impulso lineal y fuerza promedio experimenta un pasajero de 70 kg. en el auto?
Impulso (I) = m * (VF – VO)
(VF – VO) = 5,2 m/seg – 0 = 5,2 m/seg
I = m * (VF – VO)
I = 70 * (5,2) = 364 kg * m/seg
I = 364 kg * m/seg
I=F*t
F = =
t
364 kg *
seg
0,832 seg
= 437,5 kg *
m
seg 2
F = 437,5 newton
Problema 13 Serway cuatro.
Una pelota de béisbol de 0.15 Kg. se lanza con una velocidad de 40 m/seg. Luego es bateada
directamente hacia el lanzador con una velocidad de 50 m/seg. a) Cual es el impulso que recibe
la pelota?
b) Encuentre la fuerza promedio ejercida por el bate sobre la pelota si los dos están en contacto
durante 2 * 10- 3 seg. Compare este valor con el peso de la pelota y determine si es valida o no la
aproximación del impulso en esta situación.
m = 0,15 kg. masa de la pelota de béisbol
Vi = – 40 m/seg. Velocidad con la cual es lanzada la pelota de béisbol. El signo (-) por que se
desplaza hacia la izquierda
22

m
I seg
VF
I
m
VF = + 50 m/seg velocidad con la cual es bateada la pelota de béisbol. El signo (+) por que se
desplaza hacia la derecha.
?P = m VF – m Vi
?P = 0,15 * (50) – 0,15 * (-40)
?P = 7,5 + 6
?P = 13,5 kg * m/seg. = I
I = 13,5 kg * m/seg
I=F*t
13,5 kg *
F = =
t 2 *10 – 3 seg
= 6,75 *103 kg *
m
seg 2
F = 6750 newton
Compare con el peso de la pelota de béisbol
W = m * g = 0,15 * 9,8 = 1,47 Newton
Esta fuerza es muy pequeña comparado con la fuerza aplicada en el instante del bateo.
Problema 16 Serway quinta edición
Un patinador de hielo de 75 kg. que se mueve a 10 m/seg. choca contra un patinador
estacionado de igual masa. Después del choque los dos patinadores se mueven como uno solo
a 5 m/seg. La fuerza promedio que un patinador puede experimentar sin romperse un hueso es
de 4500 newton. Si el tiempo de impacto es de 0,1 seg. se rompe algún hueso?
ANTES
m1 = 75 kg
v1 = 10 m/seg
m1
m2
m2 = 75 kg
v2 =0 m/seg
DESPUES
v1
antes
v2
Después
(m1 + m2 )
(m1 + m2 ) = 75 kg + 75 kg = 150 kg.
VF = 5 m/seg
Hallamos el impulso de cada patinador después del choque.
I = m1 * Vf = 75 kg * 5 m/seg
I = 375 kg * m/seg
I=F*t
F = =
t
375 kg *
seg
0,1 seg
= 3750 kg *
m
seg 2
F = 3750 Newton
Como los huesos de cada patinador soporta 4500 newton, entonces los huesos soportan la
estrellada de los dos patinadores.
Problema 17 Serway quinta edición
23

1000 gr
Una bala de 10 gr. Se dispara a un bloque de madera estacionario (m = 5 kg.). El movimiento
relativo de la bala se detiene dentro del bloque. La rapidez de la combinación bala mas madera
inmediatamente después del choque es de 0,6 m/seg. Cual es la rapidez original de la bala?
ANTES
m1 =10 gr
v1 = ?
m1
m2
m2 = 5 kg
v2 =0 m/seg
DESPUES
m1 = 10 gr *
1 kg
= 10 – 2 kg
v1
antes
v2
Después
(m1 + m2 )
VF
(m1 + m2 ) = 10 gr + 5 kg = 10-2 kg. + 5 kg = 5,01 kg.
VF = 0,6 m/seg
(m1 * v1 ) – (m2 * v2) = (m1 + m2) * VF
(10-2 * v1) – (5 * 0) = (5,01) * 0,6
(10-2 * v1) = (3,006)
(10-2 * v1)= 3,006
V1 =
3,006
10 – 2
= 300,6
m
seg
Problema 18 Cuarta edición Serway; Problema 6 Quinta edición Serway. Problema 4 Sexta
edición Serway;
Dos bloques de masa M y 3M se colocan sobre una superficie horizontal sin fricción. Un resorte
ligero se une a uno de ellos y los bloques se empujan juntos, con el resorte entre ellos (figura
9.6) Una cuerda que inicialmente los mantiene unidos se quema y después de eso el bloque de
masa 3M se mueve hacia la derecha con rapidez de 2 m/seg.
a) Cual es la rapidez del bloque de masa M?
b) Encuentre la energía elástica original en el resorte si M = 0,35 Kg.
(+) hacia la derecha.
M = Masa del bloque pequeño de la izquierda.
VM = Velocidad del bloque pequeño de la izquierda.
3M = Masa del bloque grande de la derecha.
24

1
1
2
1
2
1
1
2
1
2
1
2
1 1 1
1
2
1 1 1
1
2
1 1 1
1
2
V3M = Velocidad del bloque grande de la derecha. = 0 2 m/seg.
– M VM = 3M * V3M
Se cancela M a ambos lados de la igualdad
– VM = 3 * V3M
– VM = 3 * 2
– VM = 6
VM = – 6 m/seg.
b) Encuentre la energía elástica original en el resorte si M = 0,35 Kg.
1
2
K X 2
=
1
2
M (VM )2 +
1
2
3M (V3M )2
K X 2
= 0,35 * (- 6)2 +
2
3 * 0,35 (2)2
1
2
K X 2
= 0,35 * (36) +
2
1
2
3 * 0,35 (4)
K X 2
= 0,35 * (18) + 3 * 0,35 (2)
K X2 = 6,3 + 2,1
K X 2 = 8,4 JULIOS
Problema 20 Serway cuatro.
Carros de aire idénticos (m = 200 gr) están equipados con resortes idénticos K = 3000 n/seg.
Los carros, que se mueven uno hacia el otro con velocidad de 3 m/seg. Sobre una pista de aire
horizontal, chocan y comprimen los resortes (Fig p9.20). Encuentre la compresión máxima de
cada resorte?
Para determinar la compresión de cada resorte X, usamos la conservación de la energía puesto
que no hay fricción ni otras fuerzas no conservativas que actúen sobre el sistema.
m v 2 + m (- V )2 = K X 2 + K (-X)2
2 2 2
0.2 (3)2 + 0,2 (- 3)2 = 3000 * X 2 + 3000 (- X )2
2 2 2
0.2 (9) + 0,2 (9) = 3000 X 2 + 3000 ( X )2
2 2 2
Cancelando ½ en la expresión
0.2 (9) + 0,2 (9) = 3000 X 2 + 3000 ( X )2
1,8 + 1,8 = 6000 X2
3,6 = 6000 X2
X 2 =
36
6000
= 0,0006
X =
0,0006
25

1 1 1
1
2
X = 2,45 * 10- 2 metros
X = 2,45 cm
Problema 20a Serway cuatro.
Carros de aire idénticos, cada uno de masa m están equipados con resortes idénticos cada uno
con una constante de fuerza K. Los carros, que se mueven uno hacia el otro con velocidades V
sobre una pista de aire horizontal, chocan y comprimen los resortes (Fig p9.20). Encuentre la
compresión máxima de cada resorte?
Para determinar la compresión de cada resorte X, usamos la conservación de la energía puesto
que no hay fricción ni otras fuerzas no conservativas que actúen sobre el sistema.
m v 2 + m (- V )2 = K X 2 + K (-X)2
2 2 2
Cancelando ½ en la expresión
m v 2 + m (- V )2 = K X 2 + K (-X)2
m v 2 + m (V )2 = K X 2 + K (X)2
2 m (V )2 = 2 K X 2
m v2 = K X 2
X 2 =
X =
m V 2
K
m V 2
K
Problema 24 Serway cuatro. Problema 20 Serway cinco.
Gayle corre a una velocidad de 4 m/seg. Y se lanza sobre un trineo que esta inicialmente en
reposo sobre la cima de una colina cubierta de nieve sin fricción. Después de que ella y el trineo
han descendido una distancia vertical de 5 metros, su hermano, que esta inicialmente en reposo,
se monta detrás de ella y juntos continúan bajando por la colina. ¿Cuál es su velocidad al final de
la pendiente si el descenso vertical total es de 15 metros?
La masa de Gayle es de 50 kg. La del trineo 5 kg. Y la de su hermano 30 kg.
VG = 4 m/seg. Velocidad de Gayle.
VT = 0 m/seg. Velocidad del trineo.
V1 = Velocidad inicial del conjunto (Gayle + trineo)
V2 = Velocidad final del conjunto (Gayle + trineo) cuando han descendido 5 metros en forma
vertical.
V3 = Velocidad inicial del conjunto (Gayle + trineo + hermano)
V4 = Velocidad final del conjunto (Gayle + trineo + hermano) al final de la pendiente
mG = masa de Gayle = 50 Kg.
mt = masa del trineo = 5 Kg.
mh = masa del hermano = 5 Kg.
26
2
1
2
2
1
2
1
2
1 2 1 2
m = masa del conjunto (Gayle + trineo) = 50 Kg. + 5 kg = 55 kg.
Mt = masa del conjunto (Gayle + trineo + hermano) = 50 Kg. + 5 kg + 30 kg. = 85 kg.
Cantidad de movimiento de Gayle antes de subirse = Cantidad de movimiento del conjunto
(Gayle + trineo)
mG * VG = m * V1
4 * 50 = 55 * V1
200 = 55 V1
V1 =
200
55
= 3,636
m
seg.
V1 = 3,636 m/seg Velocidad inicial del conjunto (Gayle + trineo)
Por conservación de energía hallamos la V2 = Velocidad final del conjunto (Gayle + trineo)
cuando han descendido 5 metros en forma vertical.
ECi + EP i = ECf + EPf
ECi =
m v1
EP i = m g h
ECf =
m v 2
EPf = 0
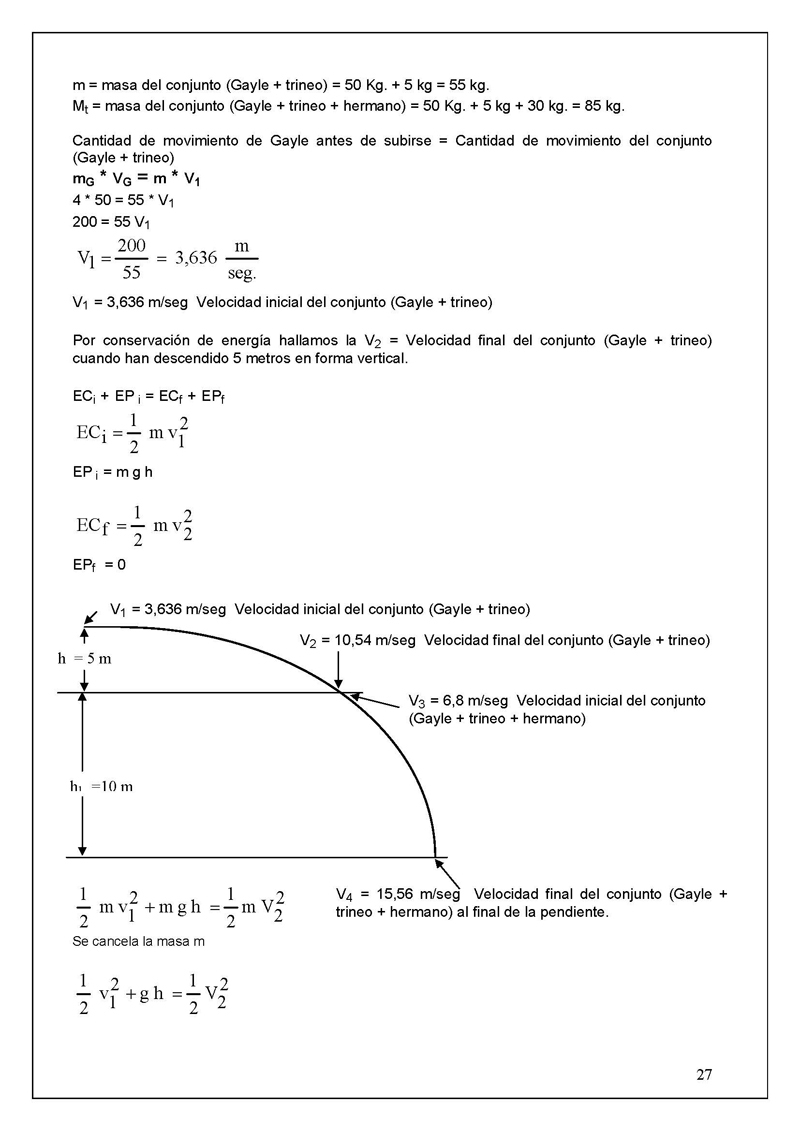
V1 = 3,636 m/seg Velocidad inicial del conjunto (Gayle + trineo)
h =5m
V2 = 10,54 m/seg Velocidad final del conjunto (Gayle + trineo)
V3 = 6,8 m/seg Velocidad inicial del conjunto
(Gayle + trineo + hermano)
h1 =10 m
2 1 2
m v1 + m g h = 2 m V2
V4 = 15,56 m/seg Velocidad final del conjunto (Gayle +
trineo + hermano) al final de la pendiente.
Se cancela la masa m
2 v1 + g h = 2 V2
27

1 2
1
2
1 2
1
2
1 2
1 2
2
2
1
2
(3,636) 2 + 9,8 * 5 = 2 V2
(13,22) + 49 = 2 V2
(6,61) + 49 = 2 V2
55,61 = 2 V2
111,22 = V2
V2 = 111,22
V2 = 10,54 m/seg. Velocidad final del conjunto (Gayle + trineo) cuando han descendido 5
metros en forma vertical.
Cuándo Gayle ha descendido con el trineo 5 metros en forma vertical, se sube al trineo el
hermano de Gayle, por lo tanto es necesario calcular V3 = Velocidad inicial del conjunto (Gayle +
trineo + hermano)
Cantidad de movimiento del conjunto (Gayle + trineo) = Cantidad de movimiento del conjunto
(Gayle + trineo + hermano)
V2 = 10,54 m/seg. Velocidad final del conjunto (Gayle + trineo) cuando han descendido 5 metros
en forma vertical.
V3 = Velocidad inicial del conjunto (Gayle + trineo + hermano)
m = masa del conjunto (Gayle + trineo) = 50 Kg. + 5 kg = 55 kg.
Mt = masa del conjunto (Gayle + trineo + hermano) = 50 Kg. + 5 kg + 30 kg. = 85 kg.
m * V2 = Mt V3
55 * 10,54 = 85 * V3
577,5 = 85 V3
V3 =
577,5
85
= 6,8
m
seg.
V3 = 6,8 m/seg Velocidad inicial del conjunto (Gayle + trineo + hermano)
Por conservación de energía hallamos la V4 = Velocidad final del conjunto (Gayle + trineo +
hermano) al final de la pendiente
h1 = 10 metros
ECi + EP i = ECf + EPf
ECi =
m v3
EP i = m g h1
28

4
1
2
1
2
1 2 1 2
1 2
1
2
1 2
1
2
1 2
1 2
2
ECf =
m v 2
EPf = 0
2 1 2
m v3 + m g h1 = 2 m V4
Se cancela la masa m
2 v3 + g h1 = 2 V4
(6,8) 2 + 9,8 *10 = 2 V4
(46,24) + 98 = 2 V4
(23,12) + 98 = 2 V4
121,12 = 2 V4
242,24 = V4
V4 = 242,24
V4 = 15,56 m/seg. Velocidad final del conjunto (Gayle + trineo+ hermano ) al final de la
pendiente
Problema 24 SERWAY quinta
Una bola de boliche de 7 kg. Choca frontalmente con un pino de 2 kg. El pino vuela hacia delante
con rapidez de 3 m/seg. Si la bola continua hacia delante con rapidez de 1,8 m/seg. ¿Cuál fue la
rapidez inicial de la bola? Ignore la rotación de la bola.
Vib = velocidad inicial del
boliche
mb = 7 kg
VFB = Velocidad final del boliche = 1,8 m/seg.
mp = 2 kg
ViP = Velocidad inicial del pino = 0
VFP = Velocidad final del pino = 3 m/seg.
29

?
Cantidad movimiento del boliche = cantidad de movimiento del pino
0
(mb
*
Vib)
+ (mp * VIp) = (mb * VFB) + (mp * VFP)
(7 * Vib) = (7 * 1,8) + (2 * 3)
(7 Vib ) = (12,6) + (6)
7 Vib = 18,6
Vib =
18,6
7
= 2,65
m
seg.
Problema 28 SERWAY SEIS.
Un defensa de 90 kg que corre al este con una rapidez de 5 m/s es tracleado por un oponente de
95 kg que corre al norte con una rapidez de 3 m/s. Si la colisión es perfectamente inelástica, (a)
calcule la rapidez y dirección de los jugadores inmediatamente después de la tacleada y (b)
determine la energía mecánica perdida como resultado de la colisión. Tome en cuenta la energía
faltante.
VF
VFY
m1 = 90 kg
V1 = 5 m/seg
m2 = 95 kg
VFX = VF cos ?
V2 = 3 m/seg
PiX : Cantidad de movimiento en el eje X antes del choque
PFX : Cantidad de movimiento en el eje X después del choque
PiY : Cantidad de movimiento en el eje Y antes del choque
PFY : Cantidad de movimiento en el eje Y después del choque
PXi
PYi
= tg ?
Movimiento en el eje X antes del choque.
PiX : Cantidad de movimiento en el eje X antes del choque = m1 * V1
m1 = 90 kg.
V1 = 5 m/seg
PiX = m1 * V1 = 90 * 5 = 450 kg * m/seg
PiX =450 Ecuación 1
Movimiento en el eje X después del choque.
Como la colisión es inelástica, quiere decir que los jugadores quedan unidos después del
choque.
VFX : Es la velocidad final en el eje x de los dos jugadores después del choque.
VFX = VF cos ? (Ver grafica)
30

 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |