 Página anterior Página anterior |   Voltar ao início do trabalho Voltar ao início do trabalho | Página seguinte  |
O modelo proposto é uma modificação do modelo apresentado por BORG & GRIMES (1986) [equação (1)] para a estimativa da profundidade efetiva do sistema radicular.
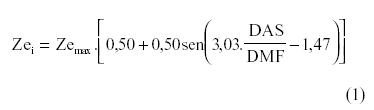
em que Zei é a profundidade efetiva do sistema radicular no i-ésimo dia após a semeadura; Zeini é a profundidade inicial do sistema radicular; Zemax é a profundidade máxima do sistema radicular; DAS é o número de dias após a semeadura; DMF é o número de dias da semeadura até o ponto de maturidade fisiológica da cultura. Mesmo não sendo lineares, esses modelos precisam apenas levar em consideração a profundidade inicial (Zeini) e máxima (Zemax), no qual não são verificadas as restrições discutidas anteriormente.
No modelo sugerido [equações (2) e (3)], o coeficiente empírico b é dependente dos parâmetros que afetam o desenvolvimento das raízes, sendo específico para cada ambiente.
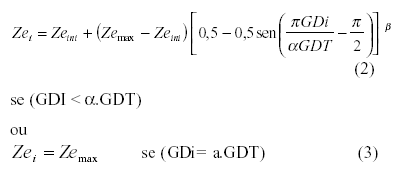
em que: GDi é a soma calórica (oC.dia) até o i-ésimo dia após a semeadura; e GDT a soma calórica (oC.dia) até ser atingido o ponto de maturidade fisiológica. A fração aGDT representa a soma calórica (oC.dia) até ser atingida a profundidade máxima do sistema radicular (Zemax), sendo a o desenvolvimento relativo correspondente à mesma. A relação GDi/GDT, corresponde então ao desenvolvimento relativo (Dri) da cultura.
Quando GDi ³ aGDT, aplica-se a equação (3) para os modelos propostos por DOURADO NETO & JONG VAN LIER (1991), SUBBAIAH & RAO (1993) e o modelo sugerido.
O modelo proposto foi validado e comparado aos modelos propostos por RASMUSSEN & HANKS (1978) [equação (4)], BORG & GRIMES (1986) [equação (1)] e SCHOUWENAARS (1988) [equação (5)].
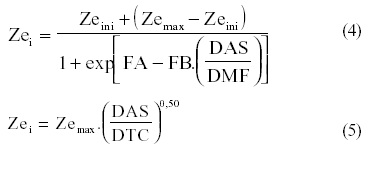
em que DAS representa o número de dias após a semeadura, DMF o número de dias da semeadura até o ponto de maturidade fisiológica da cultura, DTC a duração (dias) do ciclo da cultura; FA e FB coeficientes empíricos em função da cultura. Mesmo não sendo lineares, esses modelos precisam apenas de Zeini e Zemax nas quais também não são consideradas as restrições discutidas anteriormente. E também DOURADO NETO & JONG VAN LIER (1991) [equação 6] e SUBBAIAH & RAO (1993) [equação 7] sugerem modelos sigmoidais para a simulação do crescimento da raiz propondo a utilização de parâmetros empíricos para explicar a inter-relação da cultura com o meio:
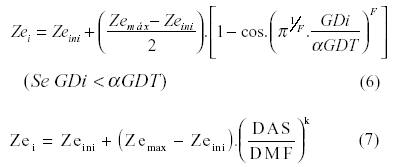
em que F e k são fatores de forma da curva de crescimento radicular e dependem dos parâmetros que afetam o crescimento das raízes. Esses coeficientes devem ser determinados por meio de análise de regressão para cada tipo particular de solo, planta e prática de manejo numa dada área geográfica durante uma época particular.
Os resultados obtidos foram comparados pelos modelos aos dados observados utilizando os resultados obtidos na cultura de milho (Zea mays L.) num solo classificado como Nitossolo Vermelho Eutroférrico, na área experimental da ESALQ, USP, em Piracicaba, SP (22º42’ S, 47º38’ W e 546 m de altitude).
A semeadura foi realizada com três híbridos (C-901, C-333-B e C-806), em 20/10/1997, sendo a colheita em 11/03/1998. Foi utilizado o delineamento inteiramente casualizado, com três repetições. Cada repetição foi constituída de 3,6 m de largura (4 linhas com espaçamento de 0,9 m) com 30 m de comprimento.
Foi utilizada uma área de 108 m2 por repetição, em populações de 60.000 plantas/ha, 50.000 plantas/ ha e 50.000 plantas/ha, respectivamente.
A amostragem do sistema radicular das plantas de milho foi realizada a campo de forma aleatória, mesmo constatando a não uniformidade no crescimento e desenvolvimento das plantas da área experimental, o que poderia influenciar nos resultados obtidos.
Para minimizar a variabilidade dos dados coletados para estimativa da profundidade efetiva do sistema radicular dos híbridos estudados foram amostradas 5 plantas por híbrido em cada repetição, nas quais foram utilizados, na análise de regressão, os valores médios.
O ciclo da cultura foi caracterizado pela soma calórica (°C.dia), conforme a aproximação pelo método direto proposta por GILMORE & ROGERS (1958). Os fatores de forma dos diferentes modelos foram determinados pela de análise de regressão não linear, com os pares de dados (GDi/aGDT) versus Zei, utilizando o método dos mínimos quadrados e o procedimento iterativo de Newton-Raphson; que minimiza a soma dos quadrados dos desvios em relação aos valores medidos e estimados da profundidade efetiva do sistema radicular.
Para efeito de estimativa de armazenamento de água disponível, assume-se o crescimento em profundidade do sistema radicular na camada de solo, responsável por cerca de 95% da evapotranspiração (camada de solo referente à zona ativa das raízes), denominada profundidade efetiva do sistema radicular.
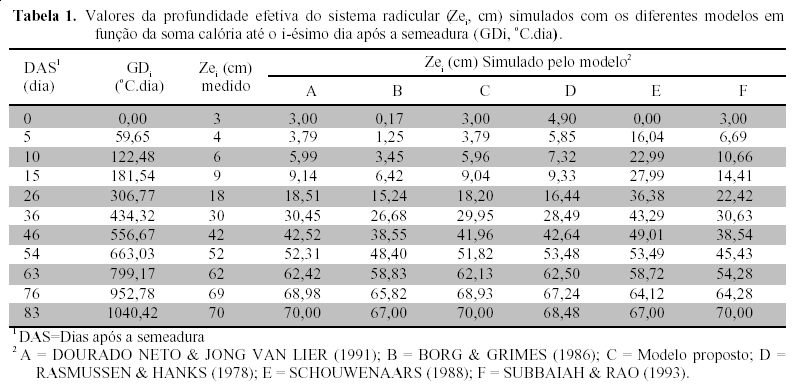
A relação temporal da curva de crescimento do sistema radicular simulada com os diferentes modelos é apresentada na Figura 1, na qual se pode verificar que, a partir de 83 DAS, a profundidade efetiva do sistema radicular é constante e igual à profundidade efetiva máxima.
Observa-se que o modelo exponencial de SCHOUWENAARS (1988) é o que menos se ajusta aos dados medidos no campo, com tendência a superestimar a profundidade efetiva do sistema radicular desde os primeiros estádios da cultura até, aproximadamente 60 dias após a semeadura, e subestimando Ze nas etapas próximas ao desenvolvimento relativo (a) correspondente à profundidade máxima atingida pela cultura.
A mesma tendência é observada no modelo proposto por SUBBAIAH & RAO (1993), mas menos acentuada na Zona I, que corresponde ao subperíodo vegetativo da cultura.
O modelo de SCHOUWENAARS (1988) e o de BORG & GRIMES (1986) apresentaram as maiores diferenças entre os valores simulados e os observados no campo para a profundidade máxima da raiz. Esse segundo modelo subestimou a profundidade de raiz ao longo do ciclo da cultura, sendo ainda menos consistente nos primeiros 20 dias após a semeadura.

A proposta de RASMUSSEN & HANKS (1978) superestima o crescimento radicular nos primeiros 15 dias após a semeadura, tendo um decréscimo na estimativa quando se aproxima a etapa de desenvolvimento relativo correspondente a profundidade máxima do sistema radicular. O melhor ajuste foi obtido com o modelo sugerido no presente trabalho e com a proposta de DOURADO NETO & JONG VAN LIER (1991). Ambos os modelos apresentaram um excelente ajuste aos dados medidos no campo ao longo do ciclo da cultura. Os valores de Ze simulados com os diferentes modelos são apresentados na Tabela 1, em que se observa a precisão obtida com a modificação do modelo de BORG & GRIMES (1986).
O coeficiente de determinação e o valor F (teste de F) foram calculados para Zona I. O alto valor de F indica uma boa aderência (maior exatidão do modelo em relação aos outros quando comparado com os dados medidos no campo). Como em todos os modelos, a partir do momento em que a profundidade efetiva máxima do sistema radicular foi atingida, a profundidade efetiva permanece constante (motivo pelo qual não se fez análise estatística para a Zona II).
Na Tabela 2, observa-se que o modelo de DOURADO NETO & JONG VAN LIER (1991) apresenta um bom ajuste aos dados medidos no campo. O modelo proposto por SCHOUWENAARS (1988) apresentou o menor valor de F e de coeficiente de determinação, sendo que SUBBAIAH & RAO (1993) obtiveram resultados semelhantes num estudo comparativo entre diferentes modelos para a simulação de crescimento radicular. A exatidão dos dados simulados em relação aos dados medidos também pode ser verificada nesta tabela. Praticamente, o coeficiente de determinação é similar nos diferentes modelos quando comparados cada um deles com os dados medidos no campo. Porém, o quadrado médio dos resíduos demonstra que, além desse modelo, as propostas de RASMUSSEN & HANKS (1978) e de SUBBAIAH & RAO (1993) são menos exatas para a simulação do crescimento radicular. O menor quadrado médio dos resíduos foi apresentado pelo modelo sugerido; seguido das propostas de DOURADO NETO & JONG VAN LIER (1991) e BORG & GRIMES (1986).
Estatisticamente, o teste F definiu que todos os modelos são altamente significativos, mas deve considerar-se que as propostas de SCHOUWENAARS (1988), SUBBAIAH & RAO (1993), BORG & GRIMES (1986) e RASMUSSEN & HANKS (1978) superestimaram ou subestimaram a profundidade efetiva do sistema radicular em certas etapas do seu desenvolvimento, o que pode ser verificado pelos valores dos coeficientes linear (a) e angular (b) da análise de comparação (Tabela 2).
Na Figura 2, os valores observados com os simulados são comparados. A maioria dos modelos tem um bom ajuste com os dados observado, mas o erro padrão é maior nos modelos de SCHOUWENAARS (1988) e SUBBAIAH & RAO (1993), como pode ser visto na Figura 2(e) e na Figura 2(f).
Na natureza, o desenvolvimento do sistema radicular das plantas no tempo não é necessariamente linear, pois as restrições inerentes ao solo como camadas de impedimento, textura, densidade e conteúdo de água, além do evidente crescimento rápido na primeira fase da cultura (SUBBAIAH & RAO, 1993) têm como resultado um crescimento lateral que não é explicado por esses modelos lineares. Uma melhor aproximação é propor modelos que considerem essas restrições.

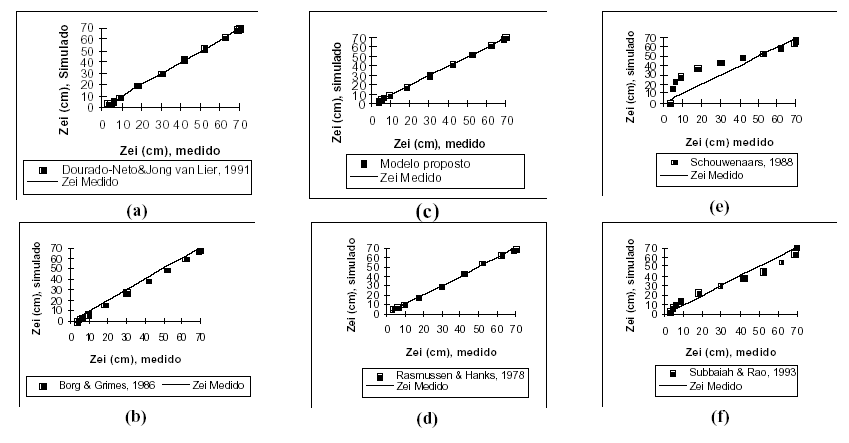
Figura 2.
Comparação dos valores simulados com os valores observados de profundidade efetiva do sistema radicular (linha 1:1) referentes à Zona I.
O modelo proposto de simulação de crescimento radicular foi o que melhor se ajustou aos dados experimentais ao longo do ciclo de desenvolvimento da cultura de milho, levando em consideração conjuntamente o quadrado médio dos resíduos, o teste F, o coeficiente de determinação e, principalmente, os coeficientes linear e angular correspondentes à análise comparativa dos modelos referentes à Zona I.
BORG, H.; GRIMES, D.W. Depths development of roots with time: an empirical description. Transaction of ASAE, St. Joseph, v. 29, n. 1, p. 194-197, 1986.
DOURADO NETO, D.; JONG VAN LIER, Q. de. Programa para elaboração do Balanço hídrico para culturas anuais e perenes. Piracicaba, Departamento de Agricultura-ESALQ, 1991. 58 p. (Manual do usuário).
DOURADO NETO, D. Modelos fitotécnicos referentes à cultura de milho. Piracicaba: Departamento de Agricultura, 1999. 229 p.
GILMORE, E.; ROGERS, J.S. Heat units as a method of measuring maturity in corn. Agronomy Journal, Madison, v. 50, p. 611-615, 1958.
RASMUSSEN, V.P.; HANKS, R.J. Spring wheat yield model for limited moisture conditions, Agronomy Journal, Madison, v. 70, p. 940-944, 1978.
SAAD, A.M. Uso do tensiômetro no controle da irrigação por pivô central. Piracicaba, ESALQ/USP, 1991. 141 p. (Dissertação de Mestrado em Irrigação e Drenagem), Escola Superior de Agricultura Luiz de Queiroz, USP, 1991.
SCHOUWENAARS, J.M. Rainfall irrigation and sowing strategies in southern Mozambique. Agriculture Water Management, Amsterdam, v. 13, n. 1, p. 49-64, 1988.
SUBBAIAH, R.; RAO, K.A. Root growth simulation model under specified environment. Journal of Irrigation and Drainage Engineering, Aragon, v. 119, n. 5, p. 898-905, 1993.
|
Revista Brasileira de Agrometeorologia, Santa Maria, v. 11, n. 2, p. 327-332, 2003. |
Paulo Augusto Manfron1,7, Osny Oliveira Santos Bacchi2,7, Durval Dourado Neto3,7,
Antônio Roberto Pereira4,7, Sandro Luis Petter Medeiros5 e Felipe Gustavo Pilau6.
manfronp[arroba]smail.ufsm.br
1. Dr. Prof. Titular. Departamento de Fitotecnia, CCR, UFSM, Santa Maria, RS.
manfronp[arroba]ccr.ufsm.br.
2. Dr. Prof. Laboratório de Física do Solo. CENA-USP. Piracicaba,SP.
osny[arroba]cena.usp.br.
3. Dr. Prof. Associado do Departamento de Produção Vegetal.-ESALQ-USP. Piracicaba, SP.
dourado[arroba]esalq.usp.br.
4. Dr. Prof. Titular do Departamento de Ciências Exatas. ESALQ-USP.Piracicaba,SP.
arpereir[arroba]esalq.usp.br
5. Dr. Prof. Adjunto Departamento de Fitotecnia, CCR, UFSM, Santa Maria, RS.
sandro[arroba]ccr.ufsm.br.
6. Engenheiro Agrônomo. Doutorando em Física do Ambiente Agrícola. ESALQ-USP.
fgpilau[arroba]esalq.usp.br.
7. Bolsista CNPq.
 Página anterior Página anterior |   Voltar ao início do trabalho Voltar ao início do trabalho | Página seguinte  |
|
|
|