 Página anterior Página anterior |   Voltar ao início do trabalho Voltar ao início do trabalho | Página seguinte  |
A agricultura moderna tem como fundamento o desenvolvimento sustentável do ponto de vista econômico e, ainda, da não-degradação do meio ambiente, porém a intensificação da exploração agrícola, aliada ao uso e manejo inadequado do solo, tem provocado o aumento da erosão, a chamada erosão acelerada (WEILL, 1999). Essa provoca o assoreamento e a poluição das áreas baixas, rios e reservatórios, podendo, até mesmo, chegar à degradação de grandes extensões de terras. A degradação do solo nos trópicos, embora reconhecida como um problema grave e generalizado, ainda carece de estudos que avaliem aspectos físicos, químicos e ambientais, de forma integrada (SCHAEFER et al., 2002). O emprego da geoestatística, com o objetivo de avaliar a estrutura espacial das variáveis, introduz nova e importante ferramenta para a análise da variabilidade espacial de atributos do solo e fatores de erosão.
O uso indiscriminado de tecnologia em áreas agrícolas no nordeste do Estado de São Paulo, onde se cultiva a cana-de-açúcar, com preparo superficial excessivo e queima dos resíduos, modifica significativamente os atributos do solo e tem promovido a degradação dos solos e, por conseqüência, do meio ambiente (FREITAS, 1987 e STONE & SILVEIRA, 2001). Nesse cenário, a erosão do solo tem papel decisivo na perda da renda líquida dos agricultores, principalmente em função da constante e elevada perda de solo e insumos que tal processo acarreta (SCHAEFER et al., 2001). Dentre os fatores naturais que afetam a erosão, o relevo condiciona o movimento da água no solo, interferindo na variação espacial dos seus atributos, sendo as rotas preferenciais dos fluxos de água que definem os mecanismos erosivos-deposicionais preponderantes. Esses fluxos, condicionados pelas feições do relevo, provocam a erosão, transportando e depositando os constituintes dos solos, ocasionando variabilidade de seus atributos. Considerando que a erosão influencia na variabilidade dos atributos do solo, pode-se assumir que a erosão dos solos, em determinada posição da paisagem, passa a ser um indicador ambiental de zonas específicas de manejo (SOUZA et al., 2002).
A erodibilidade do solo e outros fatores de erosão apresentam grande variabilidade espacial e temporal, explicada pela diversidade climática, a qual influi no potencial erosivo das chuvas, e pela variabilidade do solo, a qual tem influência na suscetibilidade à erosão (BERTOL et al., 2002). WANG et al. (2002) afirmaram que a geoestatística é importante ferramenta para o estudo dos processos de erosão, dada a sua notória variabilidade espacial. Porém, poucos trabalhos têm explorado o estudo da variabilidade espacial de fatores de erosão.
O objetivo deste trabalho foi estudar a variabilidade espacial de fatores da erosão, em área sob cultivo de cana-de-açúcar, em Latossolo Vermelho eutroférrico.
A área de estudo localiza-se no nordeste do Estado de São Paulo, no município de Guariba - SP. As coordenadas geográficas são 21º19' de latitude sul e 48º13' de longitude oeste, com altitude média de 640 m. O clima da região, segundo a classificação de Köeppen, é do tipo mesotérmico com inverno seco (Cwa), precipitação média de 1.400 mm e chuvas concentradas no período de novembro a fevereiro. A vegetação natural era constituída por floresta tropical subcaducifólia e mata ciliar.
O relevo é predominantemente suave ondulado, com declividades médias variando de 3 a 8%. A área experimental está sob cultivo de cana-de-açúcar há mais de 30 anos. O solo da área foi classificado como Latossolo Vermelho eutroférrico textura muito argilosa (LVef) (EMBRAPA, 1999).
No terço inferior da encosta, por meio da análise detalhada das formas do relevo e da variação do gradiente do declive, o solo foi amostrado em malha regular, com intervalos de 50 m, perfazendo um total de 206 pontos, georreferenciados com o uso do GPS, em área de 40 ha, na profundidade de 0,0-0,2 m.
A composição granulométrica foi determinada pelo método da pipeta, utilizando solução de NaOH 0,1N como dispersante químico e agitação mecânica em aparato de baixa rotação por 16 h, seguindo metodologia proposta pela EMBRAPA (1997), com modificações. A fração argila foi separada por sedimentação, de acordo com a lei de Stokes, sendo a fração silte determinada por diferença. A fração areia, após secagem e pesagem, foi subdividida em cinco subfrações, areia muito grossa (AMG), areia grossa (AG), areia média (AM), areia fina (AF) e areia muito fina (AMF). Para a determinação da matéria orgânica, foi utilizado o método de RAIJ et al. (1987).
A erodibilidade (fator K) foi estimada utilizando-se da equação proposta por DENARDIN (1990), a qual gerou valor médio estatisticamente semelhante ao determinado com chuva simulada no local. O fator relevo (LS) foi determinado utilizando-se de dados de comprimento de rampa e grau de declive, determinado com a equação proposta por WISCHMEIER & SMITH (1978). A erosividade das chuvas (R) local foi estimada como sendo de 7.298 MJ mm ha-1 h-1 ano-1, conforme método proposto por LOMBARDI NETO et al. (2000). O potencial natural de erosão (PNE) foi obtido com o produto R, K e LS (WISCHMEIER & SMITH, 1978). Posteriormente, integraram-se os resultados relativos aos dados de PNE com os de C e P atuais (valores obtidos para uso e a cobertura vegetal do solo, respectivamente), o que possibilitou estimar as perdas médias anuais de solo por erosão (A) para a cultura da cana-de-açúcar. O PNE foi classificado como: muito baixo (<250), baixo (250-500), moderado (500-750), alto (750-1.000) e muito alto (>1.000). Posteriormente, foram integrados os planos de informação relativos aos dados de CP atual (valores obtidos para o uso e a cobertura vegetal do solo) e CP tolerável, obtendo-se informações relativas à expectativa de erosão (EE). O risco de erosão (RE) foi determinado e classificado conforme descrito por LAGROTTI (2000). A classificação utilizada foi a seguinte: muito baixa (<1), baixa (1-2), moderada (2-5), alta (5-10) e muito alta (>10). A classificação para perda de solo foi: muito baixa (<10), baixa (10-20), moderada (20-50), alta (50-100) e muito alta (>100). O valor de tolerância de perdas de solo por erosão adotado foi de 12 t ha-1 ano-1.
A variabilidade do solo foi, primeiramente, avaliada pela análise exploratória dos dados, calculando-se a média, mediana, desvio-padrão, variância, coeficiente de variação, coeficiente de assimetria e coeficiente de curtose. A hipótese de normalidade dos dados foi testada pelo teste de Kolmogorov-Smirnov (SAS, 1995). A observação de valores extremos (máximos e mínimos) e distribuição de freqüência revelou a existência de valores atípicos para as variáveis em estudo. Após a verificação da inexistência de erros dos dados de laboratório, optou-se pela reedição dos dados extremos, por meio da média de seus vizinhos.
A análise da variabilidade, usando geoestatística, foi realizada conforme VIEIRA et al. (1983) e ROBERTSON (1998), seguindo três passos: (1) análise espacial para obter o semivariograma; (2) escolha de modelo para ajustar o semivariograma, e (3) obtenção de valores das variáveis em estudo em local não amostrado, para interpolação através da krigagem.
O uso do semivariograma em geoestatística é recomendado pela maior possibilidade de satisfazer as hipóteses de estacionaridade exigidas. O semivariograma foi estimado utilizando-se do estimador clássico:
![]()
em que, N(h) é o número de pares de valores medidos Z(xi), Z(xi + h), separados por um vetor h. O gráfico de ![]() , em função dos valores correspondentes de h, é denominado semivariograma.
, em função dos valores correspondentes de h, é denominado semivariograma.
Foram ajustados aos dados os seguintes modelos: (a) esférico (Esf), ![]() = C0 + C1 [1,5 (h/a)-0,5 (h/a)³] para 0 < h < a e
= C0 + C1 [1,5 (h/a)-0,5 (h/a)³] para 0 < h < a e ![]() = C0 + C1 para h > a; (b) exponencial (Exp),
= C0 + C1 para h > a; (b) exponencial (Exp), ![]() = C0 + C1 [1 - exp (-3 h/a)] para 0 < h < d, em que: d é a distância máxima na qual o semivariograma é definido; (c) gaussiano (Gau),
= C0 + C1 [1 - exp (-3 h/a)] para 0 < h < d, em que: d é a distância máxima na qual o semivariograma é definido; (c) gaussiano (Gau), ![]() = C0 + C1[1-exp (-3h2/a2)].
= C0 + C1[1-exp (-3h2/a2)].
O ajuste dos dados, a partir do semivariograma, possibilitou definir os seguintes parâmetros: efeito pepita (C0) - valor da semivariância quando h = 0; alcance da dependência espacial (a) - valor de h quando a semivariância se estabiliza próximo a um valor constante, e patamar (C1+C0) - valor da semivariância quando se obtém um valor constante.
A razão entre o efeito pepita e o patamar permite a classificação da continuidade espacial dos atributos do solo (TRANGMAR et al., 1985). Essa razão foi utilizada para definir as classes distintas de dependência espacial dos atributos do solo, utilizando-se da classificação de CAMBARDELLA et al. (1994).
Para determinar a existência ou não da dependência espacial, ajustaram-se semivariogramas, utilizando-se do programa GS+ (ROBERTSON, 1998). Em caso de dúvida entre mais de um modelo para o mesmo semivariograma, consideraram-se o melhor R2 (coeficiente de determinação) e o menor SQR (soma de quadrados do resíduo). Para a elaboração dos mapas de distribuição espacial das variáveis, foi utilizado o programa SURFER (1999).
Os resultados referentes à análise descritiva para as variáveis erodibilidade (K), relevo (LS), perda de solo (A), potencial natural de erosão (PNE), risco de erosão (RE) e expectativa de erosão (EE) são apresentados na Tabela 1. Os resultados referentes ao teste Kolmogorov-Smirnov indicaram normalidade apenas para a variável K. SOUZA et al. (2003), estudando a influência do relevo e erosão na variabilidade espacial de um latossolo, verificaram normalidade para a variável K.
TABELA 1. Estatística descritiva para as variáveis erodibilidade (K, t h MJ-1 mm-1), relevo (LS), perda de solo (A, t ha-1 ano-1), potencial natural de erosão (PNE, t h ano-1), risco de erosão (RE) e expectativa de erosão (EE).
|
Fatores de Erosão |
|||||||
|
Estatística |
|||||||
|
K |
LS |
A |
PNE |
RE |
EE |
||
|
Número |
206 |
206 |
206 |
206 |
206 |
206 |
|
|
Média |
0,011 |
1,13 |
4,24 |
128 |
2,96 |
-1,71 |
|
|
Mediana |
0,012 |
0,59 |
2,25 |
95 |
3,12 |
-1,81 |
|
|
DP1 |
0,002 |
1,62 |
7,71 |
174,03 |
0,94 |
0,57 |
|
|
Variância |
2,61 x 10-6 |
2,64 |
59,48 |
30.289,11 |
0,90 |
0,32 |
|
|
CV2 |
14 |
82,41 |
86,10 |
80,12 |
32,15 |
36,21 |
|
|
Assimetria |
0,14 |
2,69 |
6,10 |
1,35 |
-1,25 |
1,87 |
|
|
Curtose |
-0,16 |
3,11 |
3,11 |
6,72 |
3,65 |
3,66 |
|
|
d3 |
0,06* |
0,31 |
0,36 |
0,32 |
0,21 |
0,25 |
|
Mais importante que a normalidade dos dados é a ocorrência ou não do chamado efeito proporcional, segundo ISAAKS & SRIVASTAVA (1989) e GONÇALVES et al. (2001), o qual não foi observado nos dados das variáveis estudadas, ou seja, ocorre estacionaridade de segunda ordem, a qual pode ser observada nos patamares bem definidos dos semivariogramas ajustados (Figura 1). Para dados obtidos na natureza, o ajuste de uma distribuição teórica é apenas aproximado. A normalidade dos dados não é exigência da geoestatística, é conveniente apenas que a distribuição não apresente caudas muito alongadas, o que poderia comprometer as análises (CRESSIE, 1991).
FIGURA 1. Semivariogramas dos fatores de erosão: erodibilidade (K, t h MJ-1 mm-1), relevo (LS), perda de solo (A, t ha-1 ano-1), potencial natural de erosão (PNE, t h ano-1), risco de erosão (RE) e expectativa de erosão (EE). Esf e Exp (Co; Co+C1; a) é o modelo esférico e exponencial ajustado; Co = efeito pepita; Co+C1 = patamar; a = alcance.
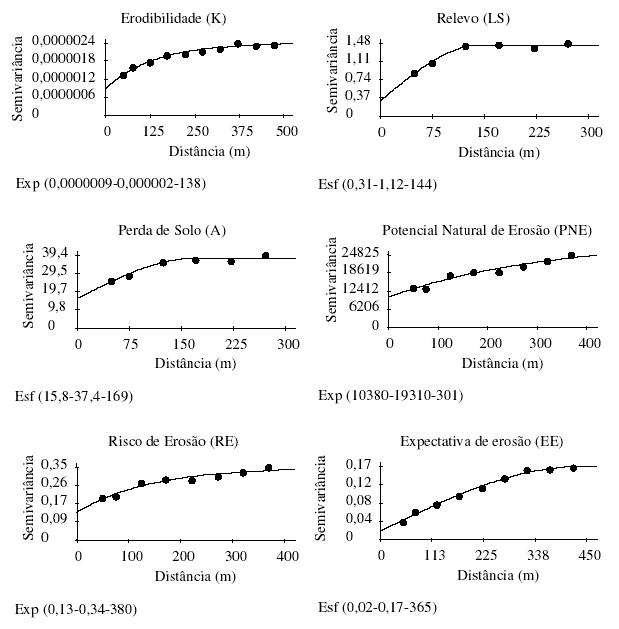
A variável K apresentou CV de 14% (Tabela 1), valor que é considerado médio segundo os critérios adotados por WARRICK & NIELSEN (1980), concordando com o resultado obtido por SOUZA (2001); já para as variáveis RE e EE, o CV foi alto (32,15 e 36,21%, respectivamente). As variáveis A, LS e PNE apresentaram valores muito altos de CV (86,10; 82,41 e 80,12%, respectivamente), estando de acordo com os resultados obtidos por MELLO (2002) e SOUZA (2001), que obtiveram valores de CV acima de 70% para essas variáveis.
Os resultados da análise geoestatística (Tabela 2 e Figura 1) mostraram que todas as variáveis analisadas apresentaram dependência espacial na profundidade estudada. O modelo exponencial ajustou-se à semivariância estimada das variáveis K, PNE e RE, concordando com o resultado obtido por MELLO (2002), que encontrou o modelo exponencial para a variável PNE, e o modelo esférico ajustou-se à semivariância estimada das variáveis LS, A e EE. SOUZA (2001) também obteve o modelo esférico para a variável A. Todas as variáveis analisadas apresentaram coeficiente de determinação (R2) acima de 0,90, ou seja, no mínimo 90% da variabilidade existente nos valores da semivariância estimada são explicadas pelos modelos ajustados. Os modelos exponencial e esférico ajustaram-se à semivariância das variáveis em estudo, estando de acordo com resultados de pesquisas que indicam esses modelos como os de maior ocorrência para os atributos do solo (SALVIANO et al., 1998).
TABELA 2. Modelos e seus parâmetros estimados nos semivariogramas experimentais para as variáveis erodibilidade (K, t h MJ-1 mm-1), relevo (LS), perda de solo (A, t ha-1 ano-1), potencial natural de erosão (PNE, t h ano-1), risco de erosão (RE) e expectativa de erosão (EE).
|
Fatores de Erosão |
||||||||||
|
Parâmetro |
||||||||||
|
K |
LS |
A |
PNE |
RE |
EE |
|||||
|
Modelo |
Exponencial |
Esférico |
Esférico |
Exponencial |
Exponencial |
Esférico |
||||
|
1C0 |
0,0000009 |
0,31 |
15,78 |
10.380 |
0,13 |
0,02 |
||||
|
2C0+C1 |
0,000002 |
1,43 |
37,45 |
29.690 |
0,34 |
0,17 |
||||
|
3a |
138 |
144 |
169 |
301 |
380 |
365 |
||||
|
4C0(C0+C1) % |
45 |
22 |
42 |
35 |
38 |
12 |
||||
|
5R2 % |
97 |
98 |
95 |
94 |
94 |
99 |
||||
|
6SQR |
2,87 x 10-14 |
5,79 x 10-3 |
7,81 |
6,51 x 106 |
1,12 x 10-3 |
1,22 x 10-4 |
||||
1 efeito pepita; 2 patamar; 3 alcance; 4 grau de dependência espacial; 5 coeficiente de determinação; 6 soma dos quadrados dos resíduos.
A relação entre o efeito pepita (C0), que é a variabilidade não explicada, e o patamar do semivariograma (C0+C1) pode indicar o grau da dependência espacial das variáveis em estudo (TRANGMAR et al., 1985). Observa-se, na Tabela 2, que as variáveis K, A, PNE e RE apresentaram dependência espacial moderada, e as variáveis LS e EE apresentaram forte dependência espacial. O alcance representa a distância em que os pontos amostrais estão dependentes espacialmente entre si (JOURNEL & HUIJBREGTS, 1991), ou seja, os pontos localizados numa área de raio menor ou igual ao alcance são mais similares. Nota-se que existiram dois grupos de alcance, ou seja, as variáveis K, LS e A apresentaram valores próximos do alcance (138; 144 e 169 m, respectivamente), e as variáveis PNE, RE e EE também apresentaram valores próximos entre si (301; 380 e 365 m, respectivamente).
Avaliando-se a porcentagem de ocorrência dos valores de PNE, A e RE para o solo em estudo (Tabela 3), nota-se que o PNE ocorre em 82% dos pontos amostrados na classe muito baixa e baixa, sendo alto e muito alto em apenas 7% dos pontos amostrados, os quais têm maior efeito do fator relevo (LS). Para a variável A, verifica-se que, em 92% dos pontos amostrados, as perdas de solo estão nas classes muito baixa e baixa, e apenas 8% dos pontos amostrados apresentam alta perda de solo. A variável RE apresenta-se com valor baixo e muito baixo em 88% dos pontos amostrados e apenas 4% apresentam RE alto, não sendo verificada a ocorrência de pontos na classe muito alta, tanto para A como para RE (Tabela 3).
TABELA 3. Porcentagem de ocorrência dos valores do potencial natural de erosão (PNE), da perda de solo (A) e do risco de erosão (RE), no Latossolo Vermelho eutroférrico (LVef).
|
Ocorrência no LVef |
Ocorrência no LVef |
Ocorrência no LVef |
|||
|
PNE |
A |
RE |
|||
|
Porcentagem |
Porcentagem |
Porcentagem |
|||
|
<250 |
75 |
<10 |
86 |
<1 |
78 |
|
250-500 |
7 |
10-20 |
6 |
1-2 |
10 |
|
500-750 |
11 |
20-50 |
7 |
2-5 |
8 |
|
750-1.000 |
7 |
50-100 |
1 |
5-10 |
4 |
|
>1.000 |
0 |
>100 |
0 |
>10 |
0 |
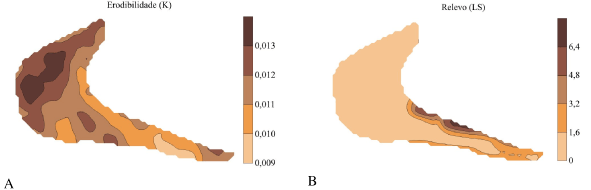
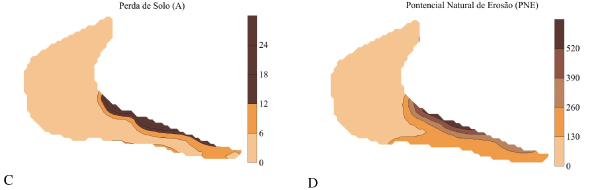
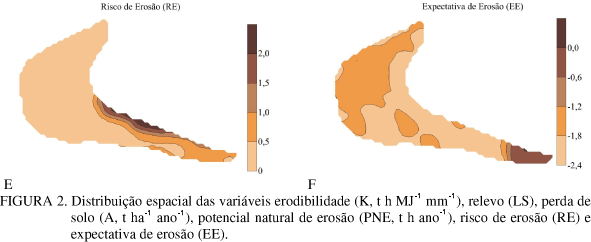
Os parâmetros dos modelos de semivariogramas ajustados foram utilizados para estimar valores em locais não amostrados por meio da krigagem (Figura 2). Por meio dos mapas de krigagem, observa-se que a variável K (Figura 2A) apresentou valores variando de 0,009 a 0,013 t h MJ-1 mm-1; a variável LS (Figura 2B) variou de 0,0 a 6,4 (baixa declividade); a variável A (Figura 2C) de 0,0 a 24 t ha-1 ano-1, e a maior ocorrência foi de muito baixa a baixa perda de solo. A variável PNE(Figura 2D) variou de 0,0 a 520 t h ano-1, mostrando maior ocorrência de valores muito baixo e baixo. Já para a variável RE (Figura 2E), os valores estiveram entre 0 e 4, porém com valores concentrando na classe muito baixo e baixo, e a variável EE (Figura 2F) variou de 0,0 a 2,4 o que caracteriza baixa expectativa de erosão para a área em estudo. De maneira geral, observa-se que as variáveis estudadas apresentaram certa tendência na área em estudo. Na região onde o relevo se encontra mais acentuado (Figura 2B), estimaram-se as maiores perdas de solo, risco de erosão e expectativa de erosão (Figuras 2C, 2E e 2F), sendo resultados semelhantes também obtidos por MELLO (2002) e SOUZA (2001).
A porcentagem de ocorrência dos valores observados para as variáveis A, PNE e RE (Tabela 2) e os mapas de krigagem das mesmas variáveis (Figura 2C, 2D e 2E) demonstram que os seus padrões de distribuição espacial na área são semelhantes, principalmente das classes com valores muito baixo e baixo para essas variáveis, e que não apresentam valores considerados muito altos, concordando com os resultados obtidos por MELLO (2002).
CONCLUSÕES
Na variabilidade do solo medida pelo coeficiente de variação, registrou-se média para erodibilidade (K), alta para o risco de erosão (RE) e expectativa de erosão (EE) e muito alta para perda de solo (A), relevo (LS) e potencial natural de erosão (PNE).
As variáveis erodibilidade (K), perda de solo (A), potencial natural de erosão (PNE) e risco de erosão (RE) apresentaram grau de dependência espacial moderado e as variáveis relevo (LS) e expectativa de erosão (EE), grau de dependência espacial forte, o que permitiu o seu mapeamento, utilizando-se de técnicas geoestatísticas.
A porcentagem de ocorrência para os valores das variáveis perda de solo (A), potencial natural de erosão (PNE) e risco de erosão (RE) e os mapas de krigagem das mesmas variáveis apresentaram padrões de distribuição espacial semelhantes para valores muito baixo e baixo dessas variáveis.
REFERÊNCIAS
Zigomar M. de SouzaI; Marcílio V. Martins FilhoII; José Marques JúniorII; Gener T. PereiraIII
zigomarms[arroba]yahoo.com.br
IDoutorando do Departamento de Solos e Adubos, Faculdade de Ciências Agrárias e Veterinárias, UNESP, Via de Acesso Prof. Paulo Donato Castellane, km 5, Jaboticabal - SP, Bolsista da FAPESP
IIProfessor Doutor, Departamento de Solos e Adubos, UNESP, Jaboticabal - SP
IIIProfessor Doutor, Departamento de Ciências Exatas, UNESP, Jaboticabal - SP
 Página anterior Página anterior |   Voltar ao início do trabalho Voltar ao início do trabalho | Página seguinte  |
|
|
|