Variabilidade espacial da estabilidade de agregados e matéria orgânica em solos de relevos diferente (página 2)

A área de estudo localiza-se no nordeste do Estado de São Paulo, no Município de Guariba, SP. As coordenadas geográficas são 21^o 19' S e 48^o 13' O, com altitude média de 640 m acima do nível do mar. O clima da região, segundo a classificação de Köppen, é do tipo mesotérmico com inverno seco (Cwa), com precipitação média de 1.400 mm, com chuvas concentradas no período de novembro a fevereiro. A vegetação natural era constituída por floresta tropical subcaducifólia.

O relevo é predominantemente suave ondulado com declividades médias variando de 3% a 8%. A área experimental está sob cultivo de cana-de-açúcar há mais de trinta anos. O solo da área foi classificado como Latossolo Vermelho eutroférrico, textura muito argilosa (Embrapa, 1999).

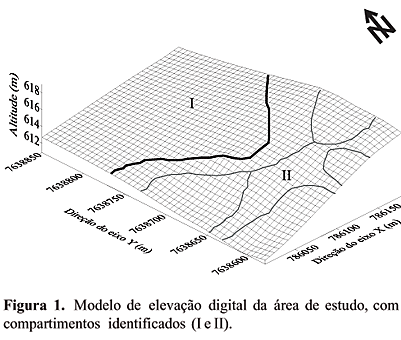
De acordo com o modelo de Troeh (1965), classificou-se a curvatura e o perfil das formas do terreno no terço inferior da encosta em dois compartimentos, I e II (Figura 1). No compartimento I, a forma do relevo é basicamente linear e o compartimento II apresenta curvaturas côncavas e convexas. O solo foi amostrado nos pontos de cruzamento de uma malha com intervalos regulares de 10 m, na linha de tráfego, nas profundidades de 0,0–0,2 m e 0,2–0,4 m. Os pontos da malha de dimensão 100x100 m, totalizando 100 pontos, em uma área de 1 ha, foram georreferenciados.

Foram abertas 100 trincheiras de 0,60 m de profundidade (0,3x0,3 m de largura), para determinação dos atributos DMG, agregados na classe >2 mm, agregados na classe 2–1 mm e MO. As amostras foram levemente destorroadas, de forma manual, e passadas em peneira de 9,51 mm de diâmetro de malha, secadas à sombra, para as análises relativas à agregação, e parte das amostras foi passada na peneira de 2,0 mm, para determinação da matéria orgânica. A separação e estabilidade dos agregados foram determinadas segundo Kemper & Chepil (1965), com modificações nas seguintes classes de diâmetro: >2,0; 2,0–1,0; 1,0–0,25; 0,25–0,10; 0,10–0,05 e <0,05 mm. Os agregados foram colocados em contato com a água sobre a peneira de 4,76 mm por quinze minutos; a massa do material retido em cada peneira foi colocada em estufa a 105^oC. Os resultados foram expressos em porcentual dos agregados retidos nas peneiras >2 mm, 2–1 mm e diâmetro médio geométrico (DMG). A determinação da matéria orgânica foi realizada conforme Raij et al. (1987).

A variabilidade do solo foi, primeiramente, avaliada pela análise exploratória dos dados, calculando-se a média, mediana, variância, coeficiente de variação, coeficiente de assimetria e coeficiente de curtose, máximo e mínimo. A hipótese de normalidade dos dados foi testada pelo teste de Kolmogorov-Smirnov (SAS Institute, 1995). A observação de valores extremos (máximos e mínimos) e distribuição de freqüência revelaram a existência de valores atípicos em relação às variáveis em estudo. Optou-se pela reedição dos dados extremos, pela média de seus vizinhos.

A teoria das variáveis regionalizadas dispõe de diferentes métodos de análise da variação espacial; um deles, o semivariograma (Vieira et al., 1983; Robertson, 1998), pressupõe a estacionaridade da hipótese intrínseca e pode ser definido como:

a qual é uma função do vetor h e, portanto, depende da magnitude e da direção h.

A semivariância é estimada pela expressão:

em que N(h) é o número de pares de pontos medidos Z(x_i), Z(x_i + h), separados por um vetor h. O gráfico de (h) contra os valores correspondentes de h é denominado semivariograma.

Do ajuste de um modelo matemático aos valores calculados de (h) são definidos os coeficientes do modelo teórico para o semivariograma (o efeito pepita, C₀; variância estrutural, C₁; patamar, C₀ + C₁; e o alcance, a). O efeito pepita é o valor da semivariância para distância zero e representa o componente da variação ao acaso; o patamar é o valor da semivariância em que a curva estabiliza sobre um valor constante; o alcance é a distância da origem até onde o patamar atinge valores estáveis, expressando a distância além da qual as amostras não são correlacionadas (Vieira et al., 1983; Trangmar et al., 1985). Foram ajustados aos dados os seguintes modelos: (a) esférico (Esf), (h) = C₀ + C₁ [1,5 (h/a)-0,5 (h/a)³] para 0<h<a e (h) = C₀ + C₁ para h>a; (b) exponencial (Exp), (h) = C₀ + C₁ [1 – exp (-3h/a)] para 0<h<d, onde d é a distância máxima na qual o semivariograma é definido.

Na determinação da existência ou não da dependência espacial, utilizou-se o exame de semivariogramas, por meio do programa GS⁺ (Robertson, 1998). Em caso de dúvida entre mais de um modelo para o mesmo semivariograma, considerou-se o melhor R² (coeficiente de determinação), menor SQR (soma de quadrados do resíduo) e validação dos modelos por meio da técnica de "Jack Knifing". Na elaboração dos mapas de distribuição espacial das variáveis foi utilizado o programa Surfer (Golden Software Inc., 1999).

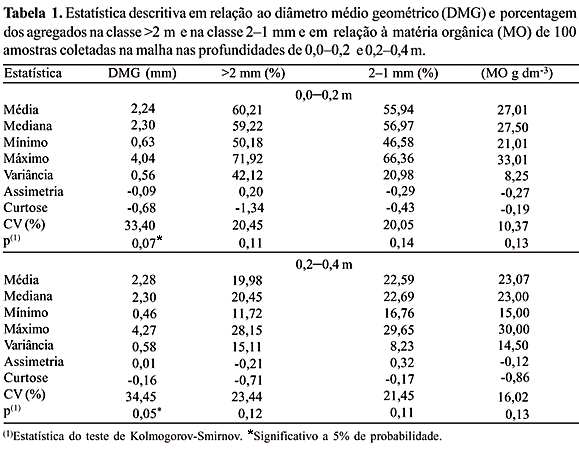
Os resultados referentes à análise descritiva para as variáveis DMG, agregados na classe >2 mm, agregados na classe 2–1 mm e MO indicaram ajuste à distribuição normal (Tabela 1). Os valores da média e mediana, para todas as variáveis, estão próximos, mostrando distribuições simétricas, o que pode ser confirmado pelos valores de assimetria próximos de zero. Os resultados referentes ao teste Kolmogorov-Smirnov indicaram normalidade para DMG em todas as profundidades. Salviano et al. (1998), Araujo (2002) e Carvalho et al. (2003) também não encontraram distribuição normal para a matéria orgânica. Souza et al. (2003) obtiveram resultado oposto a este trabalho, encontrando distribuição normal para a matéria orgânica.

Segundo Isaaks & Srivastava (1989), mais importante que a normalidade dos dados é a ocorrência ou não do chamado efeito proporcional, que a média e a variabilidade dos dados sejam constantes na área de estudo, o que foi observado, ou seja, ocorrência de estacionaridade necessária ao uso da geoestatística. No entanto, como os dados são obtidos na natureza, o ajuste de uma distribuição teórica é apenas aproximado (Warrick & Nielsen, 1980; Goovaerts, 1997; Webster, 2000).

A matéria orgânica na profundidade de 0,0–0,2 m apresentou o menor coeficiente de variação (10,4%) e o DMG, na profundidade de 0,2–0,4 m, apresentou o maior coeficiente de variação (34,5%) (Tabela 1). Adotando o critério de classificação para CV proposto por Warrick & Nielsen (1980) para medida estatística de dispersão, seus valores revelaram-se altos, médios e baixos. Foram altos (>24%), em relação à variável DMG nas profundidades 0,0–0,2 m e 0,2–0,4 m; Sá et al. (2000), estudando a estabilidade de agregados por meio da estatística clássica, encontraram CV médio para o DMG. Para as variáveis agregados na classe >2 mm e agregados na classe 2–1 mm, nas profundidades de 0,0–0,2 m e 0,2–0,4 m, e para a variável MO na profundidade de 0,2–0,4 m foram encontrados valores de CV médios, concordando com os resultados obtidos por Souza et al. (1997, 2003). Na variável MO, na profundidade de 0,0–0,2 m, os valores de CV foram baixos (12%), sendo que este resultado está de acordo com o de Pocay (2000) e Araujo (2002).

Muitos autores têm adotado essas classes de CV em trabalhos relacionados com a variabilidade espacial do solo (Macedo et al., 1998; Souza et al., 2001). Apesar de os coeficientes de variação permitirem comparar a variabilidade entre amostras com unidades diferentes, o seu emprego não deve ser generalizado, devendo-se apreciar esses resultados segundo as finalidades a que o trabalho se destina. O coeficiente de variação foi menor na camada de 0,0–0,2 m em relação à camada de 0,2–0,4 m para todas as variáveis (Tabela 1).

Os resultados da análise geoestatística mostraram que todas as variáveis analisadas apresentaram dependência espacial nas profundidades em estudo (Tabela 2 e Figura 2). O modelo esférico ajustou-se para todas as variáveis nas profundidades de 0,0–0,2 m e 0,2–0,4 m, com exceção para agregados na classe 2–1 mm na profundidade de 0,2–0,4 m que se ajustou ao modelo exponencial. Com relação ao ajuste da variável matéria orgânica, os resultados concordam com os obtidos por Souza et al. (1998) e Silva & Chaves (2001), nas profundidades de 0,0–0,2 m e 0,2–0,4 m.

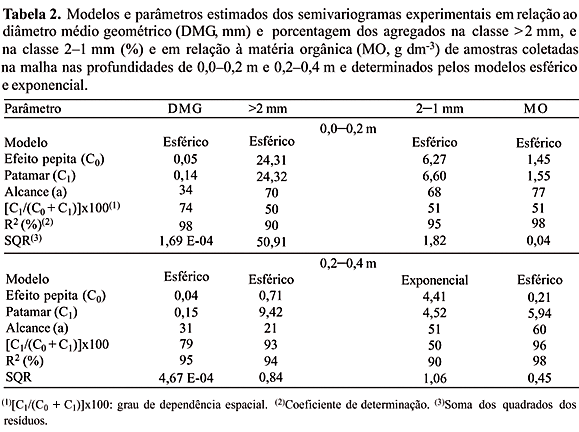
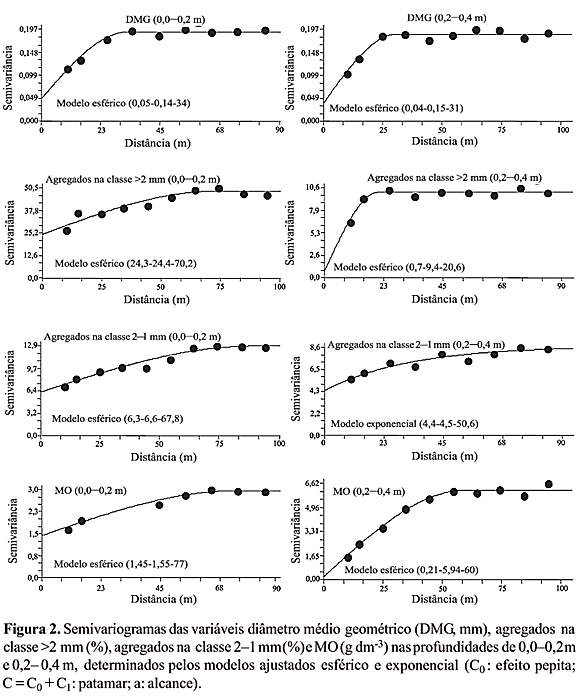
O efeito pepita é um parâmetro importante do semivariograma e indica variabilidade não explicada, considerando a distância de amostragem utilizada (McBratney & Webster, 1986). Esse parâmetro pode ser expresso como porcentagem do patamar, com o objetivo de facilitar a comparação do grau de dependência espacial das variáveis em estudo (Trangmar et al., 1985). Na análise do grau de dependência espacial das variáveis em estudo, utilizou-se a classificação de Robertson et al. (1998). A análise da relação C₁/(C₀+C₁) das variáveis DMG, agregados na classe >2 mm, agregados na classe 2–1 mm e MO mostrou que as variáveis apresentaram dependência espacial moderada na profundidade de 0,0–0,2 m. Na profundidade de 0,2–0,4 m, as variáveis apresentaram dependência espacial forte, com exceção da variável agregados na classe 2–1 mm que apresentou dependência espacial moderada (Tabela 2). O comportamento espacial da matéria orgânica concorda com os resultados obtidos por Souza et al. (1998, 2003) e Araujo (2002).

Os valores dos alcances relativos aos semivariogramas têm uma importância considerável na determinação do limite da dependência espacial, o que pode ser também um indicativo do intervalo entre unidades de mapeamento de solos (Trangamar et al., 1985; Webster, 2000). As variáveis apresentaram diferentes alcances de dependência espacial, nas profundidades de 0,0–0,2 m e 0,2–0,4 m. A variável MO apresentou o maior alcance (77 m) na profundidade de 0,0–0,2 m, e os agregados na classe >2 mm apresentaram o menor alcance (21 m) na profundidade de 0,2–0,4 m. Na profundidade de 0,2–0,4 m, os alcances foram os menores, e houve uma diminuição do alcance em profundidade em todas as variáveis, indicando a maior continuidade na distribuição espacial das propriedades do solo na camada mais superficial. Esses resultados corroboram os de Souza et al. (2001).

Os mapas das variáveis DMG, agregados na classe >2 mm, agregados na classe 2–1 mm e MO na profundidade de 0,0–0,2 m, apresentaram valores entre 1,3 e 2,7 mm, 54 e 66%, 17 e 23% e 25 e 30 g dm^-3, respectivamente (Figura 3). Na profundidade de 0,2–0,4 m, os valores variaram entre 1,3 e 2,9 mm, 49 e 65%, 20 e 26% e 19 e 26 g dm^-3, respectivamente. Houve correlação espacial do DMG e classes de agregados com o teor de matéria orgânica (Figura 3). Ocorreu redução dos valores da variável agregados na classe >2 mm e um aumento de valores da variável agregados na classe 2–1 mm na profundidade de 0,2–0,4 m, refletindo a influência do manejo da cultura da cana-de-açúcar, que recebe um tráfego de máquinas pesadas excessivo e queima dos resíduos. Corrêa (2002), comparando sistemas de preparo com mata nativa, verificou que a agregação na classe >2 mm diminui de 88,1% para 63,9% em um Latossolo Vermelho-Amarelo.

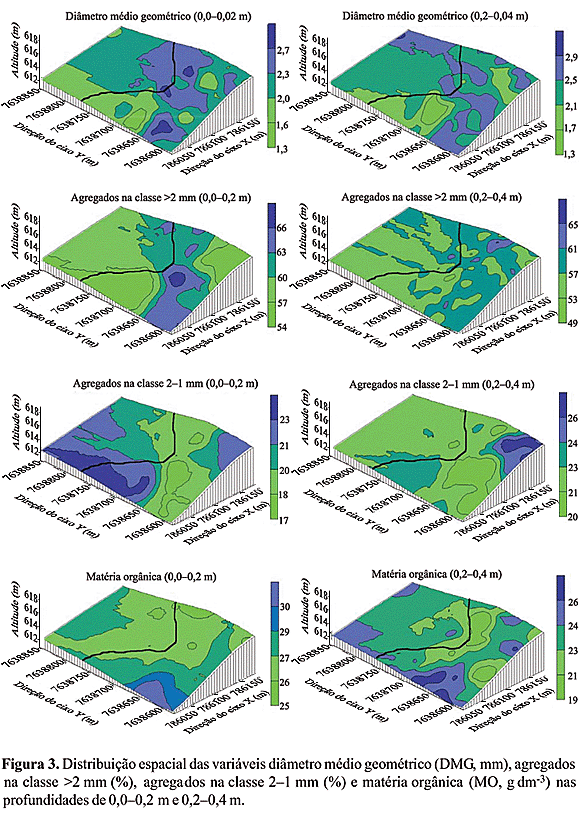
Na área onde o relevo possui forma linear (Compartimento I), observou-se os menores valores para os atributos DMG, agregados na classe >2 mm e maiores valores de agregados na classe 2–1 mm, coincidindo com os menores valores de MO em ambas profundidades. Nesse compartimento, todas as variáveis apresentaram menor variabilidade; já na área com curvaturas côncavas e convexas (compartimento II), a variação é relativamente maior (Figuras 2 e 3). Shinjo et al. (2000) encontraram relação entre posição da paisagem e variabilidade espacial de estabilidade de agregados, informando que, em áreas mais planas, a estabilidade de agregados apresentou um comportamento mais definido que em áreas mais declivosas. Bird et al. (2002) e Le Bissonnais et al. (2002) encontraram relação da estabilidade de agregados com diferentes posições na paisagem.

1. As variáveis estudadas apresentam estrutura de dependência espacial, e os maiores alcances são observados na profundidade de 0,0–0,2 m.

2. A matéria orgânica apresenta comportamento espacial similar com a estabilidade de agregados.

3. Pequenas variações no gradiente do declive e nas formas do relevo condicionam variabilidade espacial diferenciada em relação à matéria orgânica e estabilidade de agregados nas profundidades estudadas.

À Fundação de Amparo à Pesquisa do Estado de São Paulo, pela concessão de bolsa ao primeiro autor e auxílio financeiro para o desenvolvimento do projeto; à Usina São Martinho, pela concessão da área para o experimento.