Introdução

A precisão de um experimento esta intimamente relacionada ao erro experimental, que é a medida da variação não controlada ou aleatória que ocorre no experimento (Chaves, 1985). Segundo Le Clerg (1967), existem duas fontes principais de variação em experimento de campo: a primeira e mais importante é devida à heterogeneidade do solo e a segunda, decorrente da variabilidade genética do material experimental.

Além disso, o método utilizado para estimar a massa de forragem tem influência sobre a variabilidade nos resultados. O método de amostragem deve ser preciso e exato o suficiente para definir diferenças entre tratamentos que alteram a produção das pastagens.

O método destrutivo estima a produção do pasto por meio da colheita da massa de forragem em parcelas (ou subparcelas, ou amostras) de área conhecida, locadas no campo aleatoriamente, sistematicamente ou de maneira estratificada (McIntyre, 1987; Mannetje, 2000).

O formato e dimensão da moldura (parcelas, subparcelas ou amostras) e a quantidade de amostras interferem na precisão e exatidão do método utilizado para avaliação da massa de forragem (Frame, 1981).

A definição desses critérios é um dos principais problemas encontrados pelos pesquisadores visando reduzir o erro experimental decorrente da heterogeneidade das parcelas (Guzman et al., 1992).

Nesse sentido, cabe ressaltar a inferência de Bakke (1988) de que, para uma mesma espécie vegetal, o formato e o tamanho ótimo da parcela experimental devem variar, não só pela características morfológicas da planta, mas também pelas variáveis a serem avaliadas, pelo local do ensaio, pela época de coleta etc.

Para as pastagens caracterizadas pela presença de touceiras, existe a hipótese de que o formato retangular proporcionaria menor coeficiente de variação na determinação da massa de forragem, pois torna mais difícil o posicionamento da moldura entre as touceiras, ou englobando as touceiras, o que levaria a sub e superestimativas da produção de forragem, respectivamente (Mannetje, 2000).

A influência da touceira sobre o tamanho da moldura também foi ressaltada por McIntyre (1987).

Segundo esse autor, em pastagens compostas por plantas que formam touceiras, a sugestão de reduzir o tamanho da moldura e elevar o número de amostras, como tentativa de reduzir a quantidade de área amostrada e, conseqüentemente, o trabalho, não é recomendada, pois essa prática provavelmente aumenta a variabilidade amostral. Além da presença de touceiras, existem outras características morfológicas da planta que tem influência sobre o tamanho da moldura, como a altura da planta, que se relaciona positivamente com o tamanho da moldura.

De modo geral, o tamanho das molduras utilizadas para determinação da massa de forragem, geralmente, varia de 0,25 a 3,0 m2. Essas molduras podem ter formatos quadrado, retangular ou circular, com número variável de amostragens por piquete, bloco, tratamento etc (5 a 20 ) (Frame, 1981; Mannetje, 2000).

Apesar da grande amplitude dos valores apresentados, existe uma relação inversa entre o tamanho da parcela e o erro experimental. Portanto, aumento no tamanho da parcela acarreta redução da variação entre as parcelas (Steel & Torrie, 1960), o que, no entanto, não é proporcional ao aumento do tamanho da parcela, obtendo-se pouco ganho em precisão com o incremento no tamanho de unidades experimentais já suficientemente grandes (Le Clerg, 1967).

Bakke (1988) optou por molduras de formato retangular, pois esta técnica se baseia nos resultados de diversos métodos de determinação de tamanho e forma ótimos de parcelas experimentais, quando se observa, geralmente, menor coeficiente de variação com alguns tipos de parcelas retangulares. Além disso, o formato retangular torna a operação de colheita mecanizada da forragem mais eficiente (Penati & Corsi, 1998). Por esses motivos, a recomendação mais freqüente em relação ao tamanho e forma de parcelas experimentais indica o uso de parcelas retangulares e pequenas, em detrimento das parcelas quadradas e grandes (Bakke, 1988).

Além do tamanho e formato da moldura, outro aspecto da técnica experimental relacionado à precisão dos resultados de um experimento refere-se ao número de repetições (Gomes, 1987). O erro-padrão da média de um tratamento, obtido de um experimento, é dado por s/(r-1/2), em que s é o desvio-padrão residual em nível de parcela e r, o número de repetições (Steel & Torrie, 1960). O número ótimo de repetições está associado ao tamanho da moldura, ou seja, quanto maior a moldura, menor a necessidade de amostras para se obter o mesmo nível de precisão (Chaves, 1985). Esse autor avaliou o efeito da quantidade e tamanho da parcela sobre o desviopadrão médio na avaliação de progênie de milho.

Para o parâmetro produção de grãos, a regressão entre o desvio-padrão médio (sm), o número de repetições (R) e o tamanho da parcela (A) foi sm= 23,21 * R-1/2 * A –0,3708. Dessa forma, sm foi de 16, 9, 5 e 3 para as combinações 2 repetições: 1 m2, 2 repetições: 5 m2, 20 repetições: 1 m2 e 20 repetições: 5 m2, respectivamente. Observa-se que a variabilidade da amostra foi reduzida com o aumento do número de repetições e/ou tamanho da parcela. Entretanto, o diferencial na redução da variabilidade entre as combinações diminui com valores mais elevados do número e tamanho das parcelas (Le Clerg, 1967).

Objetivou-se, neste trabalho, determinar a melhor combinação entre a relação dimensão:formato da unidade amostral (moldura) e a quantidade de amostras (repetição) necessárias para avaliar a massa de forragem em pastagens com hábito de crescimento cespitoso.

Material e Métodos

Foram conduzidos três experimentos para deteminar a melhor relação dimensão:formato da unidade amostral e a quantidade de amostras Número de Amostras e Relação Dimensão:Formato da Moldura de Amostragem para Determinação da... 38 necessárias para avaliação da massa de forragem.

Para os três experimentos utilizou-se um delineamento em blocos completos casualizados, arranjados em um esquema fatorial. Os fatores foram representados pelo número de amostras e pela relação dimensão:formato da moldura. Após os dados serem testados para homogeneidade da variância e normalidade, procedeu-se à análise de variância (SAS, 1989). Quando os valores de F foram significativos, compararam-se as médias dos valores referentes à dimensão:formato da unidade amostral e ao número de amostras pelo teste t-student (nível significativo de 5%). Para a massa de forragem, quando os valores de F foram significativos, utilizou-se o teste Tukey a 5% de significância.

O primeiro experimento foi realizado no Departamento de Produção Animal da Escola Superior de Agricultura Luiz de Queiroz, em pastagem de capim-elefante (Pennisetum purpureum Schum.) formada há cerca de 30 anos (Faria et al., 1996) e manejadas de forma intensiva em um sistema de pastejo rotacionado. Este experimento foi realizado nos meses de março, abril e maio de 1999, em piquetes com aproximadamente 2.000 m2, cuja pastagens estavam com 30 a 40 dias de rebrota após o último pastejo.

Foram utilizados três conjuntos de piquetes, denominados C (0,6 ha), D (2,0 ha) e F (2,2 ha) – cada um considerado um bloco (repetições) no delineamento estatístico de bloco ao acaso. Em cada conjunto de piquetes, foram empregados os tratamentos referentes à relação dimensão:formato da unidade amostral (0,25 m2 quadrado - 0,25Q; 0,25 m2 retangular - 0,25R; 1,0 m2 quadrado - 1,00Q; 1,0 m2 retangular - 1,00R; 2,0 m2 quadrado - 2,00Q; 2,0 m2 retangular - 2,00R; 3,0 m2 quadrado - 3,00Q e 3,0 m2 retangular - 3,00R) e o número de amostras (2 a 8).

A moldura utilizada para demarcar os locais das coletas (Figura 1), com dimensão de 1,73 x 3,00 m, foi dividida em duas partes para facilitar o manuseio. As divisões internas na moldura foram feitas para estabelecer as áreas 1 a 20 (Figura 1), que, em combinações específicas, formaram as oito relações entre dimensão e formato pretendidas de modo que, por exemplo, a massa de forragem coletada, rente ao solo, nas áreas da moldura que representam 0,25Q (áreas 1 e 2 da Figura 1) foram utilizadas, para compor a amostra referente ao tratamento 1,00Q (áreas 1, 2, 3, 4, 5 e 6 da Figura 1). As divisões internas na moldura também foram projetadas para o formato retangular, indepen- Figura 1 - Croqui das duas metades da moldura com as divisões internas (1 a 20) proporcionando diferentes relações dimensão:formato. Os valores nos eixos horizontal e vertical são expressos em cm.

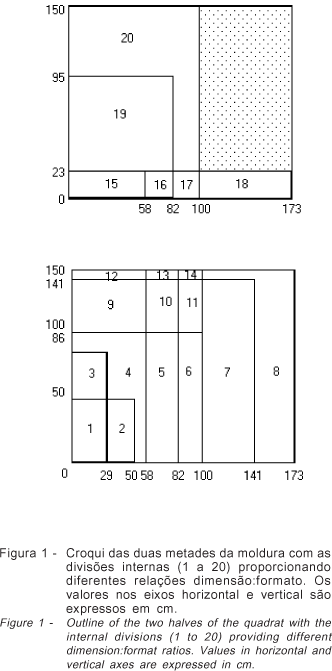
As amostragens foram realizadas aleatoriamente com o lançamento de uma parte da moldura no piquete.

Tomando-se essa peça como ponto de referência, montou-se a moldura. Neste experimento, não se determinou o teor de matéria seca da forragem. Portanto, os valores foram expressos em matéria original.

O segundo e terceiro experimentos foram executados no período de 22 de setembro a 29 de outubro de 1999, em pastagem de capim-tanzânia (Panicum maximum Jacq. cv Tanzânia) manejadas em um sistema rotacionado de pastejo. A planta forrageira foi estabelecida, em 17 de março de 1999, na Fazenda Areão, pertencente ao Campus "Luiz de Queiroz", Universidade de São Paulo, em Piracicaba-SP.

Os piquetes de capim-tanzânia utilizados tinham área de 1.333 m2.

Os protocolos experimentais desses estudos foram iguais aos descritos para o experimento 1. No entanto, nesses experimentos, considerou-se a massa seca de forragem. Além disso, os tratamentos de 3 m2 foram eliminados e o número de amostras passou de oito para nove. Essas alterações foram feitas em decorrência dos resultados obtidos no experimento 1.

Além desse aspecto, a quantidade de blocos passou de três para quatro, em virtude do delineamento experimental da área de capim-tanzânia, que foi planejada com quatro blocos, porque a área era mais heterogênea que a área estabelecida com capim-elefante.

Foram coletadas nove amostras por bloco (repetições) para atender ao tratamento relativo ao número de amostras, aplicando-se em cada ponto de coleta todos os tratamentos referentes à relação dimensão:formato da unidade amostral. A diferença entre os experimentos 2 e 3 foi o momento da amostragem realizada um dia antes e um dia após o pastejo, respectivamente. O período de descanso e de ocupação nesse sistema de pastejo foi de 33 e 3 dias, respectivamente.

O primeiro ciclo de pastejo da área estabelecida com capim-tanzânia abrangeu o período de 16 de agosto a 21 de setembro de 1999. Nesse ciclo de pastejo, foi feita a uniformização da pastagem utilizando machos castrados da raça Nelore (média de 200 kg de peso vivo). Os experimentos 2 e 3 foram realizados durante o segundo ciclo de pastejo, de 23 de setembro a 30 de outubro de 1999.

Resultados e Discussão

Nos experimentos 1 e 2, não se observou interação entre a relação dimensão:formato da moldura e o número de unidades amostrais para as variáveis coeficiente de variação (CV%) e massa média de forragem. Dessa forma, consideraram-se os fatores separadamente (efeitos principais). Nas Tabelas 1 e 2, são apresentados os resultados para os experimentos 1 e 2, respectivamente.

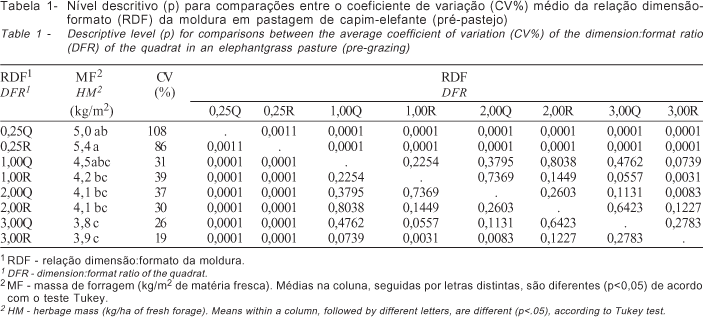
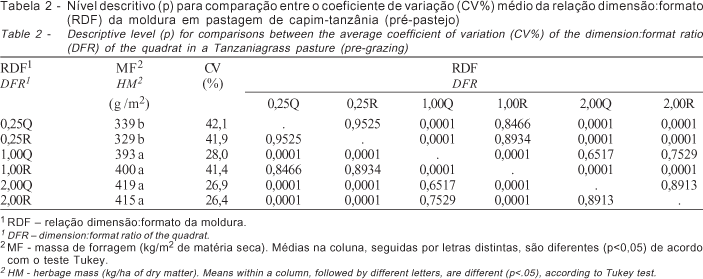
Tomadas como referência as relações com os menores CV% (3,00R e 2,00R nas Tabelas 1 e 2, respectivamente), observa-se que a relação dimensão:formato 1,00Q é a de menor área que não difere dos tratamentos 3,00R e 2,00R nos experimentos 1 e 2, respectivamente. Esse resultado corrobora a afirmação de Le Clerg (1967) de que o aumento do tamanho da parcela diminui o CV%, mas essa redução não é proporcional ao aumento no tamanho da parcela.

Portanto, o incremento no tamanho da unidade amostral de 1 m2 para 2 m2 não reflete em reduções significativas do CV%.

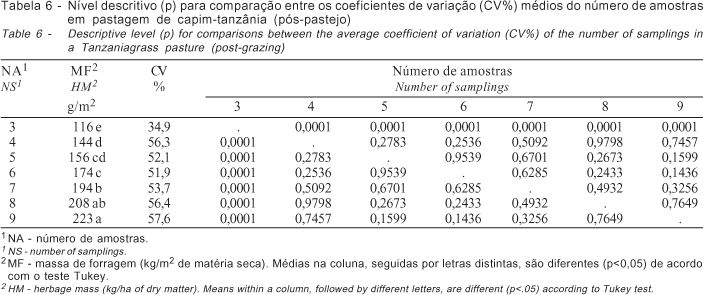
O número de amostras também teve efeito sobre o CV% (Tabelas 3 e 4). A expectativa era de que o aumento do número de amostras diminuísse o CV%, entretanto, isso não ocorreu. Resultados semelhantes foram apresentados em trabalho de revisão feito por McIntire (1987), que enfatiza a importância de definir o ponto de estabilização do CV% com o aumento do número de unidades amostrais.

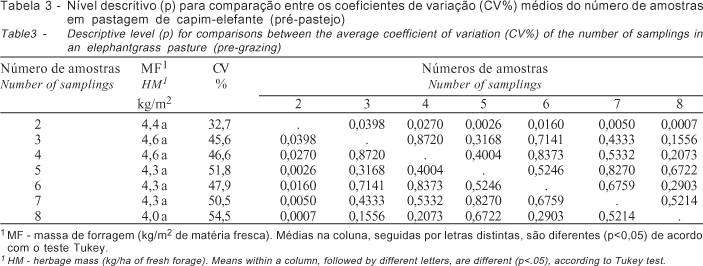
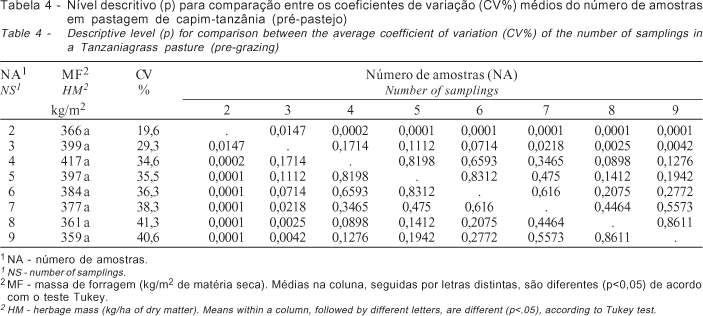
Nesse contexto, é importante determinar a quantidade de amostras a partir da qual o valor do CV% apresenta menor variação, ou seja, passa a ser constante, independentemente do aumento no número de amostras. Nesse sentido, os resultados das Tabelas 3 e 4 indicam que, a partir de três e quatro amostras, não existe diferença (p>0,05) entre os CV% para os experimentos 1 e 2, respectivamente.

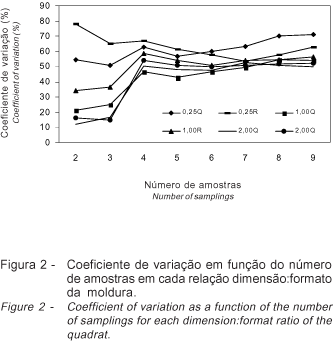
No experimento 3 (capim-tanzânia pós-pastejo), houve interação significativa entre os fatores número de amostras e relação dimensão:formato da unidade amostral. A análise exploratória dos dados, no entanto, evidenciou grande variabilidade nas observações referentes ao tratamento duas amostras (Figura 2), indicando que esse grupo de observações poderia ser excluído da análise. Assim, uma nova análise (sem os dados referentes ao tratamento com duas amostras) não detectou interação significativa entre os fatores, sendo possível avaliar os efeitos principais dos fatores número de amostras e relação dimensão:formato da moldura de forma independente.

Nas Tabelas 5 e 6, estão os níveis descritivos (p) da análise estatística dos resultados do experimento 3, desconsiderando-se o tratamento com duas amostras.

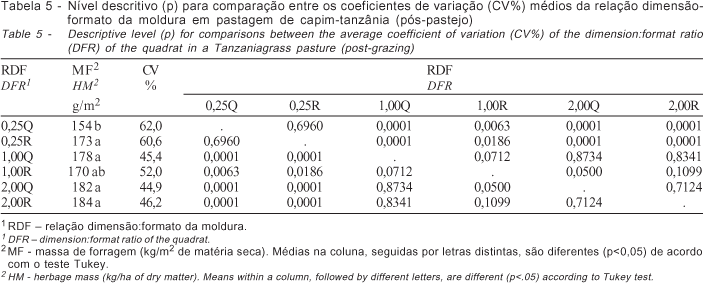
As relações com 1 m2 de área não diferem da relação com o menor CV% (2.00R) (Tabela 5), enquanto, a partir de 4 amostras, não ocorreram diferenças no CV% (Tabela 6). Essa evidência está coerente com a Figura 3, em que as combinações com as maiores quantidades de interações similares (p<0,05) são 4 amostras de 1 m2 no formato quadrado (4 x 1Q) e 5 amostras de 1 m2 no formato quadrado (5 x 1Q). Observa-se, também, na Figura 3 que, a partir de quatro amostras de 1 m2 (forma quadrada), houve tendência de estabilização no CV%.

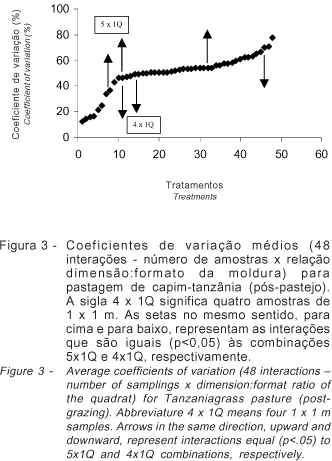
Os resultados observados são semelhantes aos obtidos por Guzman et al. (1992). Esses autores estimaram a massa de forragem em pastagens de capim-elefante estabelecidas em relevos planos e inclinados por intermédio do critério da estabilização do CV% para determinar o melhor tamanho e formato da unidade amostral. Os pesquisadores utilizaram o método da máxima curvatura do coeficiente de variação (MCCV) e máxima curvatura do coeficiente de variação modificado (MCCVM) utilizando um ensaio em branco. Concluíram que, pelo método da MCCV, o tamanho ideal da unidade amostral estava entre 1,0 e 1,75 m2 no relevo plano e entre 1,25 e 1,75 m2 no relevo inclinado. Utilizando-se o método MCCVM, o tamanho seria de 1,0 m2 e 1,5 m2 para os relevos plano e inclinado, respectivamente.

Guzman et al. (1992) também indicaram que o formato retangular seria mais indicado, pois os CV% foram menores para esse formato que para a forma quadrada. Entretanto, nesse trabalho, não há informações sobre o procedimento estatístico dessa comparação. Infere-se, portanto, que os CV% observados nos formatos retangulares e quadrados não seriam diferentes, pois os valores dos CV% foram próximos entre os formatos (20,5; 17,8; e 20,1% para os formatos 0,5 x 2,0 m; 2,0 x 0,5 m e 1,0 x 1,0 m no relevo plano, respectivamente, e 18,1; 11,2; 17,6 e 17,2% para os formatos 0,5 x 3,0 m; 3,0 x 0,5 m; 1,0 x 1,5 m e 1,5 x 1,0 m no relevo inclinado, respectivamente).

Em revisão sobre o assunto, Bakke (1988) comenta o trabalho de ensaio em branco feito conduzido por Gomez & Gomez (1984), em que a variabilidade dos resultados coletados nas parcelas retangulares foi menor que nas parcelas quadradas. Entretanto, o CV% foi diferente entre as parcelas retangulares dispostas perpendicular e as dispostas paralelamente ao eixo principal do experimento, o que dá suporte à afirmação de Chaves (1985) de que parcelas retangulares são indicadas quando a área experimental (ou parcela) é heterogênea, em função de algumas características relacionadas ao solo – retenção de umidade, fertilidade do solo, entre outros. Nessa situação, o uso de formato retangular pode tornar as parcelas mais homogêneas entre si, apesar de aumentar a heterogeneidade dentro da parcela.

O melhor resultado observado neste experimento, da moldura de 1,00Q em relação a 1,00R, pode estar associado a uma possível fonte de erro na colheita da forragem no perímetro da parcela, pois a moldura dificulta a operação de corte (Mannetje, 1987; Whaley & Hardy, 2000). Esse tipo de erro é menor no formato quadrado que no retangular, pois a relação perímetro:área é menor no formato quadrado e diminui com o aumento da área (800, 920, 400, 462, 282 e 327 cm/m2 para 0,25Q; 0,25R; 1,00Q; 1,00R; 2,00Q e 2,00R, respectivamente). Além disso, no perímetro da moldura, pode haver dúvida quanto à localização da touceira (ou da planta ou do perfilho), ou seja, é difícil definir se ela faz parte da parcela ou não. Dessa forma, pode ocorrer corte de plantas (ou parte delas) que estão fora da parcela ou, analogamente, pode haver falhas devido à não amostragem de plantas que deveriam ser colhidas (Mannetje, 2000).

Conclusões

A avaliação da massa de forragem em pastagens formadas com plantas de hábito de crescimento cespitoso deve ser feita com quatro amostras por piquete, sendo recomendado o uso de molduras de 1 m2 (1m x 1m). Essa combinação entre número de amostras e formato:dimensão da unidade amostral determina menor coeficiente de variação, garantindo maior confiabilidade à estimativa da produção de forragem com maior eficiência no processo de amostragem.

Agradecimento

À Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), pelo financiamento deste estudo.

À Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), pela concessão da bolsa de estudo ao primeiro autor.

Literatura Citada

• BAKKE, O.A. Tamanho e forma ótimos de parcelas em delineamentos experimentais. Piracicaba: Escola Superior de Agricultura Luiz de Queiroz, 1988. 142p. Dissertação (Mestrado em Agronomia) - Escola Superior de Agricultura Luiz de Queiroz, 1988.
• CHAVES, J.C. Tamanho da parcela para seleção de progênies de milho (Zea mays L.). Piracicaba: Escola Superior de Agricultura Luiz de Queiroz, 1985. 148p. Tese (Doutorado em Agronomia) - Escola Superior de Agricultura Luiz de Queiroz, 1985.
• FARIA, V.P.; PEDREIRA, C.G.S.; SANTOS, F.A.P. Evolução do uso de pastagens para bovinos. In: SIMPÓSIO SOBRE MANEJO DE PASTAGENS, 13., 1996, Piracicaba. Anais... Piracicaba: Fundação de Estudos Agrários Luiz de Queiroz, 1996. 1-14.
• FRAME, J. Herbage mass. In: HODGSON, J.; BAKER, R.D.; DAVIES, A. et al. (Eds.) Sward measurement handbook. Berkshire: British Grassland Society, Hurley: Grassland Research Institute, 1981. p.39-70.
• GOMES, F.P. Curso de estatística experimental. 12.ed. Piracicaba: Nobel, 1987. 465p.
• GOMEZ, K.A.; GOMEZ, A.A. Statistical procedures for agricultural research. 2.ed. New York: John Wiley, 1984. 680p.
• GUZMAN, G.A.B.; NASCIMENTO JR., D.; REGAZZI, A.J. et al. Estudo do tamanho e forma ideal da unidade amostral na avaliação da disponibilidade de matéria seca em pastagens. I – Método da máxima curvatura do coeficiente de variação. Revista da Sociedade Brasileira de Zootecnia, v.21, n.3, p.396-405, 1992.
• LE CLERG, E.L. Significance of experimental design in plant breeding. In: FREY, K.J. (Ed.) Plant breeding. Ames, Iowa State University Press. 1967. p.243-314.
• MANNETJE, L’t. Measuring quantity of grassland vegetation. In: MANNETJE, L’t (Ed.) Measurement of grassland vegetation and animal production. Berkshire: CAB International Bureau of Pastures and Field Crops, 1987. p.96-95.
• MANNETJE, L.’t Measuring biomass of grassland vegetation. In: MANNETJE, L.’t; JONES, R.M. (Eds.) Field and laboratory methods for grassland and animal production research. Wallingford: CAB International, 2000. p.151-177.
• McINTYRE, G.A. Statistical aspects of vegetation sampling. In: MANNETJE, L. (Ed.) Measurement of grassland vegetation and animal production. Berkshire: CAB International Bureau of Pastures and Field Crops, 1987. p.8-21.
• PENATI, M.A.; CORSI, M. Condições técnicas para localização e instalação da exploração leiteira. In: SIMPÓSIO SOBRE PRODUÇÃO ANIMAL, 10., 1998, Piracicaba. Anais... Piracicaba: Fundação de Estudos Agrários Luiz de Queiroz, 1998. p.7-55.
• STATISTICAL ANALYSES SYSTEM - SAS. SAS/STAT user’s guide. Version 6.11. Cary, 1989. 943p.
• STEEL, R.G.D.; TORRIE, J.H. Principles and procedures of statistcs. New York: McGraw-Hill Book Company, 1960. 481p.
• WHALEY, R.D.B.; HARDY, M.B. Measuring botanical compoistion of grasslands.In: In: MANNETJE, L.’t; JONES, R.M. (Eds.) Field and laboratory methods for grassland and animal production research. Wallingford: CAB International, 2000. p.67-102.

Recebido em: 04/02/03 // Aceito em: 17/11/04

Marco Antonio Penati /2, Moacyr Corsi /3, Cesar Gonçalves de Lima /4, Geraldo Bueno Martha Júnior /5, Carlos Tadeu da Silva Dias /6
mailto:ctsdias[arroba]carpa.ciagri.usp.br

1. Parte da tese de doutorado apresentada à Escola Superior de Agricultura "Luiz de Queiroz", Universidade de São Paulo (ESALQ/USP), Piracicaba-SP, pelo primeiro autor. Projeto financiado pela FAPESP.
2. Engenheiro Agrônomo, Doutor, Departamento de Produção Animal – ESALQ/USP. Av. Pádua Dias, 11, C.P. 9, 13418-900, Piracicaba-SP (mapenati[arroba]esalq.usp.br).
3. Professor Titular, Departamento de Produção Animal – ESALQ/USP (moa[arroba]esalq.usp.br).
4. Professor Doutor, Departamento de Ciências Básicas, FZEA/USP. C.P. 23, 13630-970, Piracicaba-SP (cegdlima[arroba]usp.br).
5. Pesquisador, Embrapa Cerrados. BR020, km 18, C.P. 08223, 73301-970, Planaltina-DF (gbmartha[arroba]cpac.embrapa.br).
6. Professor Doutor, Departamento de Ciências Exatas – ESALQ/USP. Av. Pádua Dias, 11, C.P. 29, 13418-900, Piracicaba-SP.