Modelos para estimativa do subfator cobertura-manejo (CiII) relativo à erosão entressulcos (página 2)

O trabalho foi conduzido em área experimental da Fazenda de Ensino, Pesquisa e Produção (FEPP) da Faculdade de Ciências Agrárias e Veterinárias, Câmpus da UNESP, em Jaboticabal - SP, num Latossolo Vermelho (LV). A área experimental foi mantida sem a presença de vegetação e de seus resíduos por 12 meses. O delineamento experimental adotado foi o inteiramente casualizado, num esquema fatorial com cinco níveis de resíduo vegetal de milho e quatro níveis de declividade e com duas repetições, totalizando 40 parcelas.As parcelas, com dimensões de aproximadamente 0,50 m de largura por 0,75 m de comprimento (0,38 m²), foram delimitadas com chapas metálicas nas suas laterais e parte superior e, na extremidade inferior, por uma calha convergente para uma saída de 0,10 m de diâmetro, recebendo o solo, sete dias antes das realizações dos testes, uma aração e duas gradagens no sentido do declive. Os gradientes de declives médios utilizados foram de 5,3%; 10,4%; 15,3% e 36,2%. Para as simulações de chuvas, com a conseqüente produção de sedimentos erodidos nas parcelas entressulcos, foi utilizado um simulador de chuvas de hastes rotativas, tipo Swanson, com bicos veejet 80100, previamente calibrado e nivelado no terreno, como proposto por SWANSON (1965). As intensidades de chuvas foram determinadas dispondo-se 36 pluviômetros alinhados no sentido do declive, como descrito por PEREIRA & MOLINA (1986). Uma chuva de 55,0 mm h^-1 foi aplicada 24 horas antes dos testes experimentais, durante 20 minutos, para uniformizar a umidade dos solos. Para evitar danos na superfície dos solos, foram utilizadas telas plásticas, tipo sombrite, para dissipar a energia das gotas da água da chuva nas parcelas, de modo semelhante ao adotado por PEREIRA (1989). Posteriormente, as parcelas foram cobertas com lona plástica para evitar perdas de água por evaporação e danos devidos à eventual ocorrência de precipitações naturais. No dia do teste final, foi efetuada a distribuição de palha de milho correspondente ao tratamento destinado a cada parcela, com cinco doses de resíduos de milho aplicadas na superfície e nas bordaduras das parcelas: 0,00; 0,05; 0,15; 0,40 e 0,80 kg m^-2. A porcentagem de área de solo coberta foi avaliada com uma régua graduada de 0,50 m, conforme método descrito por ADAMS & ARKIN (1977). Depois de 24 horas da chuva de 55,0 mm h^-1, outra chuva com intensidade média de 66,7 mm h^-1 foi aplicada durante 60 minutos. Uma segunda seqüência de chuvas foi realizada, em outras 20 parcelas, utilizando-se dos mesmos tratamentos e procedimentos experimentais já descritos para as 40 parcelas experimentais da primeira série de chuvas. Os resultados obtidos nessas 20 parcelas constituíram um banco de dados utilizado no processo de validação de modelos.Amostragens para medidas de vazões dos escoamentos superficiais e das concentrações de sedimentos foram realizadas no quinto minuto após o início da enxurrada e, a partir daí, a cada cinco minutos. As amostras foram coletadas em recipientes de vidro, cronometrando-se o tempo de coleta. Em seguida, os recipientes foram fechados e conduzidos ao laboratório para a quantificação da concentração de sedimentos e do volume de solução, e conseqüente determinação das taxas de perdas de solo (D_i) e água (R).As análises estatísticas foram realizadas utilizando-se do programa estatístico STATISTICA (STATSOFT, 1994). No processo de validação, foi realizada medida da acuracidade das predições de modelos utilizados neste estudo, pela análise do grau de coincidência desses valores estimados para com aqueles observados no campo. O programa foi utilizado, ainda, para análises de variância, regressões lineares e não-lineares. Para os testes de validação dos modelos propostos na literatura, foram utilizados parâmetros estatísticos propostos por LOAGUE & GREEN (1991) e LENGNICK & FOX (1994), tais como:

Erro-padrão da estimativa normalizado (RMSE),

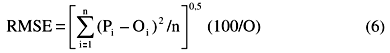
Coeficiente de determinação (CD),

Eficiência do modelo (EF),

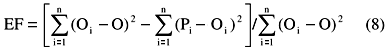
Coeficiente de massa residual (CRM),

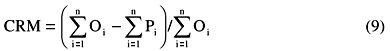
Erro máximo (ME),

Diferença média (MD),

em que,

O_i - valor observado;
P_i - valor predito;
i - índice de 0 a n;
n - espaço amostral, e
O - média dos valores observados.

Os parâmetros RMSE, CD e ME têm limite inferior igual a zero. O RMSE é semelhante ao coeficiente de variação e foi utilizado para comparar a acurácia da simulação para os tratamentos. O máximo valor para EF é a unidade. EF, CRM e MD podem ser negativos. Para os casos em que EF foi menor que 1, considerou-se que o modelo prediz valores piores do que o simples uso da média dos valores observados. O CD foi utilizado como medida da proporção da variância total explicada pelos dados preditos. Quando o MD apresentou sinal (+) ou (-) foi assumido que os valores preditos, em média, superestimavam ou subestimavam os valores observados, respectivamente.Como não há um padrão para a validação de modelos, quando os valores preditos e observados eram os mesmos, considerou-se que os parâmetros estatísticos RMSE, CD, EF, CRM, ME e MD assumem valores iguais a 0; 1; 1; 0; 0 e 0, respectivamente. Os valores de RMSE, CD, EF, CRM, ME e MD foram obtidos, caso a caso, com o programa STATISTICA.

O efeito da cobertura do solo por resíduos de milho em contato direto com a superfície do solo, subfator C_iII, foi determinado com o modelo (2) (C_iII = D_i / (K_i I R S_f) ), em que D_i é a taxa média de erosão entressulcos, observada nas parcelas com coberturas do solo, obtida nos 15 últimos minutos das amonstragens de enxurrada. Os valores de D_i obtidos nas parcelas sem cobertura, nos 15 últimos minutos das amostragens de enxurrada, foram utilizados para estabelecer a erodibilidade entressulcos (K_i ). O fator declividade (S_f ) foi determinado como citado em MARTINS FILHO (1999):

em que,

Os valores médios do subfator Ci_II obtidos com o uso dos modelos (2) e (5) são apresentados na Tabela 1.

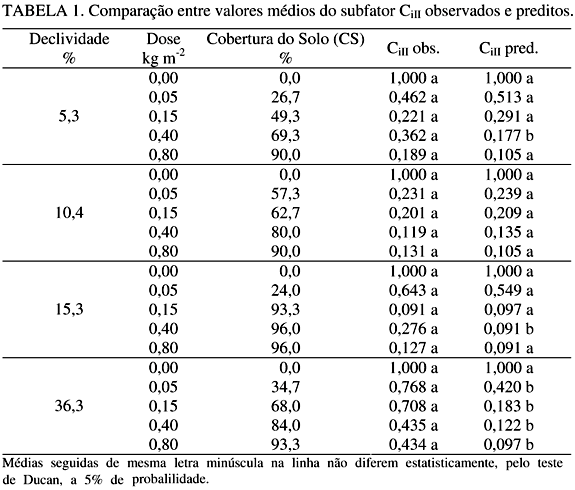
Para as doses de 0,05 kg m^-2, a palha de milho reduziu a área exposta ao impacto das gotas em 26,7%; 57,3% e 24%, para os respectivos declives de 5,3%; 10,4% e 15,3% (Tabela 1). Considerando-se os valores do subfator C_iII observados (0,462; 0,231 e 0,643) para declives de 5,3%; 10,4% e 15,3%, é possível afirmar que houve reduções de 53,8%; 76,9% e 35,7% nas taxas de erosão entressulcos, respectivamente. Assim, é possível dizer que 27,1%; 19,6% e 11,7% da redução nos valores de D_i, para os respectivos declives de 5,3%; 10,4% e 15,3%, são devidos aos efeitos da palha de milho sobre o transporte de sedimentos pelo fluxo superficial e, ainda, a uma possível redução da taxa de desagregação pelo aumento da profundidade do fluxo, como observado por BRAIDA (1994).

Alguns valores do subfator C_iII observados e os estimados com a eq.(5), proposta por LAFLEN et al. (1985), diferiram significativamente entre si, principalmente nos tratamentos em que a declividade média do terreno foi de 36,3% (Tabela 1). Assim, é possível questionar o uso generalizado da equação proposta por LAFLEN et al. (1985). Em função desse fato, procedeu-se uma análise de regressão com o objetivo de calibrar os parâmetros da eq.(5) na predição do subfator C_iII. Na Tabela 2, as equações ajustadas (13 a 17), para a determinação do subfator C_iII , são apresentadas conforme o declive do terreno.

As eqs.(5) e (13) a (17) foram comparadas, quanto aos seus desempenhos, para o subfator C_iII. O banco de dados necessário aos testes de validação foi aquele obtido em 20 parcelas experimentais, com a segunda série de chuvas. Na Tabela 3, são apresentados os parâmetros estatísticos relativos ao desempenho das eqs. (5 ) e (13) a (17), na predição do subfator C_iII.

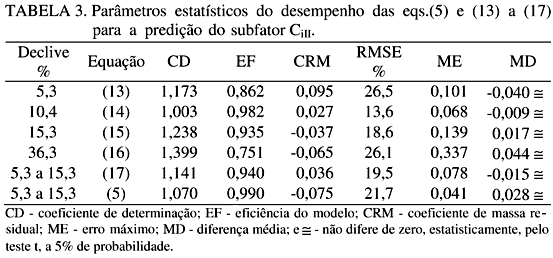
Os coeficientes de determinação (CD) foram utilizados para uma avaliação da proporção de valores observados, explicados pelos valores preditos. Os referidos coeficientes permitiram inferir que, na maioria dos casos testados, as equações permitiram boas estimativas dos valores observados do subfator C_iII. Idealmente, o valor desejável de CD é 1,0 quando se obtém um ajuste perfeito entre valores observados e estimados. Os valores de CD mantiveram-se todos próximos ao valor ideal 1,0 (Tabela 3). Os menores valores de CD foram obtidos com o uso das eqs. (5) e (14) para declives de 10,4% e 5,3% a 15,3, respectivamente.Com relação à eficiência (EF), em declives de 36,3%, pode-se inferir que a eq.(16) foi a que apresentou o menor EF (Tabela 3). Já para declives de 5,3% a 15,3%, a equação mais eficiente foi a (5). O EF não avalia apenas a linearidade dos valores observados, mas também as diferenças relativas entre valores observados e estimados (RISSE et al., 1993). Um valor de EF igual a 1,0 indica um modelo perfeito, o que não foi o caso.Os valores estimados por todas as equações testadas (Tabela 3) alternam situações de tendência à subestimação e superestimação dos valores observados do subfator C_iII. Segundo ZACHARIAS et al. (1996), valores negativos de CRM indicam superestimativas dos valores observados, quando estimados por uma equação. LENGNICK & FOX (1994) observaram que o sinal positivo de MD sugere, em média, que os valores estimados superestimam os observados. Assim, CRM > 0,0 e MD < 0,0 indicam que os valores observados do subfator C_iII são subestimados pelos valores preditos, pelo uso das eqs.(13), (14) e (17). Contudo, os valores de MD, para todos os casos testados, não diferiram significativamente de 0,0 pelo teste t. Dessa forma, é possível dizer que os desvios médios entre valores observados e estimados do subfator C_iII não permitem inferir sobre quais são as melhores equações.Os erros nas predições do subfator C_iII, utilizando-se das eqs.(13) a (16), variaram de 13,5% a 26,5% (Tabela 3). Já quando foram utilizadas as eqs.(5) e (17), os erros foram da ordem de 21,7% e 19,5% . Pôde-se observar que os erros nas estimativas geradas por todas as equações testadas foram elevados. A utilização das eqs.(13) a (16) conduziram a erros máximos da ordem de 0,101; 0,068; 0,139 e 0,337, respectivamente. Quando se desconsideraram as parcelas com 36,3% de declividade média, os erros máximos cometidos, com as eqs.(5) e (17), foram da ordem de 0,041 e 0,078, respectivamente. Em função do exposto, não se pode inferir quais equações foram as melhores.

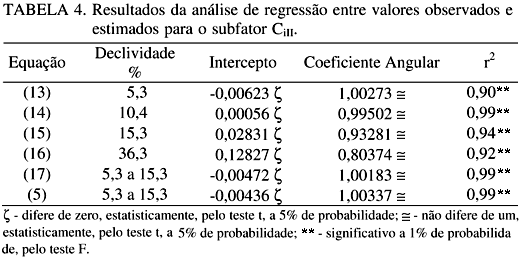
De acordo com LENGNICK & FOX (1994), quando há uma significante associação entre valores observados e preditos, testes adicionais de coincidência podem ser realizados pela simples comparação do intercepto e da inclinação com 0,0 e 1,0, respectivamente. Na Tabela 4, apresenta-se a análise de regressão entre valores observados e estimados para o subfator C_iII. Essa análise permitiu confirmar, utilizando-se das eqs.(13) a (16), nas condições testadas no presente trabalho, para a predição do subfator C_iII, que haverá subestimativas dos valores observados em declives de 5,3% e 10,4% e, ainda, superestimativas nos declives de 15,3% e 36,3% (Tabela 3). Pelos resultados da Tabela 4, verifica-se que as eqs.(5) e (17) superestimam e subestimam os valores observados do subfator C_iII, respectivamente.

As equações C_iII = e ^{-2,50 CS/100} e C_iII = e ^{–2,238 CS/100} permitem boas estimativas do subfator C_iII , para declives de 5,3% a 15,3%.

Para declives médios de 36,3%, recomenda-se o uso da equação C_iII = e ^{-0,795 CS/100}, para o LV estudado, até que outras pesquisas sejam efetuadas, a fim de que melhor calibração possa ser determinada para locais com declives acentuados.

• ADAMS, J.E.; ARKIN, G.F. A light interception method for measuring row crop ground cover. Soil Science Society of America Journal, Madison, v.41, n.1, p.789-92, jan./feb. 1977.BRAIDA, J.A. Relações da erosão entressulcos, com resíduos vegetais em cobertura e erosão em sulcos em solo Podzólico Vermelho-Escuro. 1994. 152 f. Dissertação (Mestrado em Ciência do Solo) - Universidade Federal do Rio Grande do Sul, Porto Alegre, 1994.BROWN, L.C.; FOSTER, G.R.; BEASLEY, D.B. Rill erosion as affected by incorporated crop residue and seasonal consolidation. Transactions of the ASAE, St. Joseph, v.32, n.6, p.1967-78, july/aug. 1989.FOSTER, G.R. Modeling the erosion process. In: HAAN, C.T.; JOHNSON, H.P.; BRAKENSIEK, D.L. Hydrologic modeling of small watersheds. St. Joseph: American Society of Agricultural Engineers,1982. p.296-380. (Monograph, 5) LAFLEN, J.M.; FOSTER, G.R.; ONSTAD; C. Simulation of individual storm soil losses for modeling the impact of soil erosion on cropland productivity. In: EL-SWAFY, MULDENHAUER AND LO (Ed.). Soil erosion and conservation. Ankeny: SCSA, 1985. p.285-95.LATTANZI, A.R.D.; MEYER, L.D.; BAUMGARDNER, M.F. Influences of mulch rate and slope steepness on interrill erosion. Soil Science Society of America Journal, Madison, v.38, n.6, p.946-50, nov./dec. 1974.LENGNICK, L.L. ; FOX, R.H. Simulation by NCSWAP of seasonal nitrogen dymanics in corn: I. soil nitrate. Agronomy Journal, Madison, v.87, n.1.p.167-75, 1994.LOAGUE, K.; GREEN, R.E. Statistical and graphical methods for evaluating solute transport models: overview and application. Journal of Contaminant Hydrology, Amsterdam, v.7, n.1, p.51-73, jan. 1991.MARTINS FILHO, M.V. Modelagem do processo de erosão entressulcos em latossolos de Jaboticabal - SP. 1999. 140 f. Tese ( Doutorado em Solos e Nutrição de Plantas) - Universidade Federal de Lavras, Lavras, 1999.NEARING, M.A.; FOSTER, G.R.; LANE, L.J.; FINKNER, S.C. A process-based soil erosion model for USDA - Water erosion prediction project technology. Transactions of the ASAE, St. Joseph, v.32, n.5, p.1587-93, 1989.PEREIRA, V.P. Perda de solo em Latossolo Vermelho-Escuro, textura argilosa, devida a impacto de gotas de chuva simulada e a comprimento de rampa. 1989. 106 f. Tese (Livre-Docência em Conservação do Solo) - Faculdade de Ciências Agrárias e Veterinárias, Universidade Estadual Paulista, Jaboticabal, 1989.PEREIRA, V.P. ; MOLINA, D.S. Método para medição da intensidade de chuva produzida por um simulador de hastes rotativas. In: CONGRESSO BRASILEIRO, 6., ENCONTRO NACIONAL DE PESQUISA SOBRE CONSERVAÇÃO DO SOLO, 6., 1986, Campo Grande. Resumos... Campo Grande: Fundação Cargil, 1986. p.69.RISSE, L.M.; NEARING, M.A.; NICKS, A.D.; LAFLEN, J.M. Error assessment in the universal soil loss equation. Soil Science Society of America Proceedings, Madison, v.57, n.3, p.825-33, may/june 1993.STATSOFT. Statistica: Quick reference. Tulsa, 1994. 148 p.SWANSON, N.P. Rotating-boom rainfall simulator. Transactions of the ASAE, St. Joseph, v.8, n.1, p.71-2, jan./feb. 1965.WISCHMEIER, W.H. Estimating the soil loss equations cover and management factor for undisturbed areas. In: SEDIMENT YIELD WORKSHOP, 1972, Oxford. Present and prospective technology for predicting sediment yields and sources. Washington: USDA, 1975. p.118-24. (ARS-S-40)ZACHARIAS, S.; HEATWOLE, C. D.; COAKLEY, C. W. Robust quantitative techniques for validating transport models. Transactions of the ASAE, St. Joseph, v.39, n.1, p.98-102, jan./feb. 1996.ZHANG, X.C.; NEARING, M.A.; MILLER, W.P.; NORTON, L.D.; WEST, L.T. Modeling interrill sediment delivery. Soil Science Society of America Proceedings, Madison, v.62, n.2, p.438-44, mar./apr., 1998.