Estimativa de parâmetros para o planejamento de experimentos com a cultura do pimentão em área restr (página 2)

Foram realizados dois experimentos na UFSM (RS) (latitude: 29°43'23''S, longitude: 53°43'15''W e altitude: 95 m). O solo do local onde foram realizados os experimentos pertence à unidade de mapeamento São Pedro, classificado como Brunizem Hidromórfico. A estufa plástica possui dimensões de 24 m de comprimento por 10 m de largura, com pé-direito de 2 m e de 3,5 m na parte central. Toda a cobertura, bem como as cortinas móveis das laterais e das portas, foram feitas de filme de polietileno de baixa densidade (PEBD), com espessura de 100 micras e com aditivo anti-UV.

A produção das mudas do pimentão, cv. Vidi, foi realizada pelo sistema de bandejas de isopor, suspensas sobre uma armação metálica, no interior de uma estufa-sementeira, com cobertura plástica e irrigação com microaspersores. O transplante das mudas foi realizado na segunda quinzena do mês de fevereiro de 2001 e na primeira quinzena do mês de setembro de 2001 para as estações sazonais verão-outono e inverno-primavera, respectivamente. Os experimentos foram cultivados em 10 fileiras de 70 plantas cada, sendo o espaçamento de 0,6 m entre as fileiras e 0,3 m entre as plantas. As fileiras foram demarcadas sobre camalhões com 0,1 m de altura e 0,4 m de largura, sendo os mesmos cobertos com mulching preto de PEDB, de 35 micras de espessura.

O preparo do solo foi realizado com enxada rotativa. Procedeu-se a adubação química de acordo com os resultados da análise do solo, seguindo as recomendações oficiais para a cultura. A irrigação foi efetuada por gotejamento por meio de tubos-gotejadores, os quais foram instalados sob o mulching. A quantidade de água irrigada foi definida com base na tensão da água no solo, em cada fileira de plantas, controlada por meio de hidrômetros tipo unijatos de baixa vazão. A condução das plantas no interior das estufas foi realizada em haste única, via fios de ráfia verticais, sustentados por arames de aço, fixados na altura do pé-direito da estufa. Os tratos culturais foram uniformemente executados, em toda a estufa, para caracterizar um ensaio em branco, de acordo com o desenvolvimento da cultura e os tratamentos fitossanitários foram definidos em função de levantamentos semanais de controle. O manejo da temperatura no interior da estufa foi controlado apenas com ventilação natural, por meio da abertura e do fechamento das cortinas laterais.

A unidade básica (UB) foi composta por uma planta e resultou em 70 unidades básicas em cada uma das 10 fileiras. As plantas foram identificadas com etiquetas, contendo o número de ordem da fila e da planta dentro de cada fila. Os frutos colhidos, em cada data de colheita, foram colocados em sacos plásticos identificados e depois levados para a contagem do número de frutos e a para pesagem.

Foram planejados tipos de parcelas com variação do tamanho e da forma. Cada tipo de parcela teve X1 unidade básica de largura (filas) e X2 unidade básica de comprimento (colunas), formado pelo agrupamento de unidades contíguas, de modo que X1*X2 corresponde a X (tamanho da parcela em número de unidades básicas). Os 20 tipos de parcela planejados (Tabela 1) são divisores de 10 filas e de 70 colunas do ensaio. Dessa maneira, o número de repetições de cada tipo de parcela ficou limitado pela área total da estufa plástica.

Para a variável valor acumulado da fitomassa dos frutos por planta, foram planejados 20 tipos de parcelas e estimados os seguintes parâmetros: N = 700/X = número de parcelas com X unidades básicas (UB) de tamanho; M(x) = média das parcelas com X UB de tamanho; V(x) = variância entre as parcelas de X UB de tamanho; VU(X)= V(X)/X² = variância por UB entre as parcelas de X UB; CV(x) = coeficiente de variação entre as parcelas de X UB de tamanho. A partir desses parâmetros, foi estimado o índice de heterogeneidade do solo "b", segundo a relação empírica - VU(x)=V1/X^b - de Smith, para o valor acumulado da fitomassa dos frutos por planta (Storck, 1979). O valor de "b" foi estimado como um coeficiente de regressão linear, através da logaritmização da equação de Smith, ponderada pelos graus de liberdade (Steel et al., 1997) - log VU(x) = log V₁ — b log X.

Lessman e Atkins (1963) concluíram que, se a relação empírica de Smith é precisamente ajustada, a função CV(x) = A/X^B se ajustará da mesma forma, porque CV(x) = , onde a M(x) é uma medida do tamanho de parcela em termos da determinação da fitomassa dos frutos, pois a M(x) é a média de uma determinada parcela de tamanho X, isto é, M(x) = X*M(1) onde M(1) é a média das parcelas de uma UB. O coeficiente B mede a associação entre o CV(x) e o tamanho da parcela, e a estimativa de A é a estimativa do CV(1). Pelas comparações descritas acima, as constantes A e B da equação geral do CV(x) transformada em logarítimo, são estimadas pela equação - log{CV(x)} = log(A) — b log(X) — ponderada pelos graus de liberdade.

Com essas informações, foi estimado o tamanho ótimo de parcela por três diferentes métodos: o da máxima curvatura, o da comparação das variâncias e o de Hatheway.

Para o método da máxima curvatura construiu-se um gráfico, colocando-se o coeficiente de variação no eixo das ordenadas e a área da parcela, em número de UB´s, no eixo das abcissas. O tamanho ótimo (Xo) da parcela, por inspeção visual, é o ponto de máxima curvatura no gráfico.

Para o método da comparação das variâncias, foram procedidos os cálculos da variância reduzida — VR(x)=V(x)/X de acordo com Vallejo e Mendonza (1992) e Ortiz (1995). Em seguida, aplicaram-se consecutivos testes de Bartlett, em nível de 5% de probabilidade de erro, para verificar a homogeneidade das variâncias (Steel et al., 1997), sendo excluída a parcela com menor número de UB após cada teste em que as variâncias foram consideradas heterogêneas. Ao se obter um grupo de parcelas com variâncias homogêneas, escolheu-se como tamanho ótimo de parcela o de menor número de UB´s.

Hatheway (1961) propôs um método que não leva em consideração os custos de obtenção das informações, utilizados no método de Smith. Fez isso combinando a fórmula de Cochran e Cox (1968) para a determinação do número de repetições, a partir da relação de Smith. A fórmula desse método considera o coeficiente de variação estimado para a parcela de uma UB, o número de repetições previsto (r), o índice de heterogeneidade do solo, os valores da distribuição "t" de Student e a diferença mínima significativa entre médias de dois tratamentos medida em porcentagem da verdadeira média (d) d² = 2(t₁ + t₂)² A² / r X^b; onde: t₁=t_á1(gl); t₁=t_á2(gl) para gl igual a infinitos graus de liberdade; á=0,05; á₂=2(1-P); r = 4, 8 e 16 repetições; A= estimativa do coeficiente de variação das parcelas de uma UB obtido da função CV(x)=A/X^B; e a probabilidade de rejeitar a hipótese de P = 0,80.

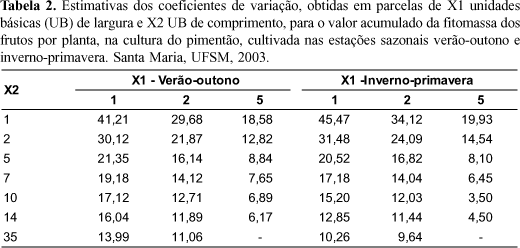
Observa-se que os valores dos coeficientes de variação apresentaram uma grande amplitude, tanto na estação sazonal verão-outono (6,17 a 41,21%) quanto na estação sazonal inverno-primavera (3,50 a 45,47%) (Tabela 2). Essa variabilidade para o valor da fitomassa acumulada dos frutos, por planta, ocorreu porque as colheitas foram realizadas quando os frutos se tornavam maduros e porque os frutos amadureciam com tamanhos diferentes, em vista das alterações nas condições fisiológicas ou de variações significativas das condições ambientais. Constatou-se também que os valores dos coeficientes de variação dos diferentes tamanhos e formas das parcelas planejadas, diminuíram à medida que se aumentou o tamanho da parcela (aumento da largura e/ou do comprimento). Este comportamento já era esperado, pois concordou com a maioria dos trabalhos que estudaram o tamanho e a forma de parcela (Storck, 1979; Oliveira e Estefanel, 1995 e Zanon e Storck, 2000), independentemente da cultura avaliada.

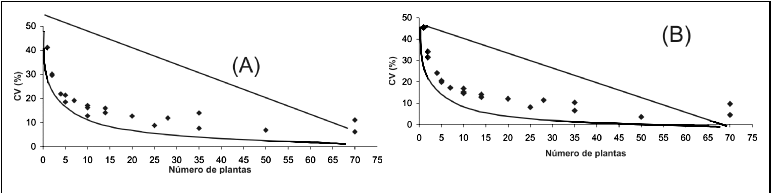
Na figura 1 A e B estão representados os gráficos entre a relação do coeficiente de variação com o tamanho e a forma das parcelas. Elas indicam que as parcelas com mais de dez plantas apresentaram pouca redução na variabilidade. Conseqüentemente, pelo método da máxima curvatura, o tamanho e a forma de parcela adequados foram de dez plantas, sendo duas no comprimento e cinco na largura, para os experimentos realizados com pimentão, independente da estação de cultivo.

A redução do CV(x) não foi linear em relação ao aumento do tamanho da parcela. Esta, no início, foi mais acentuada e, mais adiante, teve uma tendência à estabilidade. Dessa forma, observa-se que o aumento do tamanho das parcelas é vantajoso até determinado ponto, pois, a partir dele, a utilização de áreas maiores não é compensada pelos baixos ganhos na precisão.

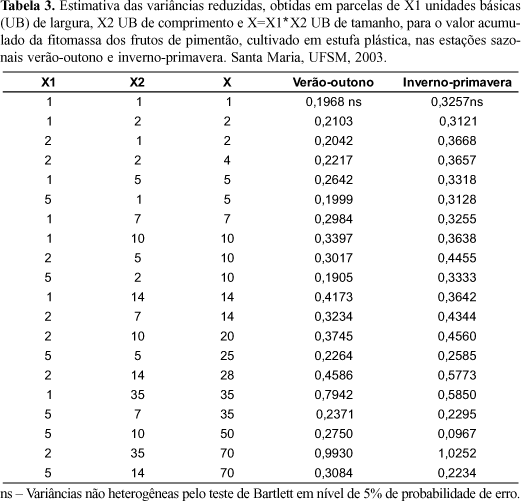
Já pelo método da comparação das variâncias, nota-se que todas as variâncias reduzidas, dos diferentes tamanhos e formas de parcelas utilizados nos experimentos com pimentão (estação sazonal verão/outono e estação sazonal inverno/primavera), foram homogêneas pelo teste de Bartlett. Tal resultado indica que o tamanho e a forma ótimos para os experimentos de pimentão são aqueles que constituem a parcela de uma unidade básica, ou seja, uma planta (Tabela 3).

Para o método de Hatheway, os valores estimados dos índices de heterogeneidade do solo "b" e da estimativa de "A" da função CV(x)=A/X^B, aplicados à fórmula de cálculo da diferença mínima significativa, foram respectivamente de 0,721 e 35,87%, para a estação sazonal verão-outono; e de 0,994 e 46,63%, para a estação sazonal inverno-primavera. Esses valores mostram o quanto a área nesta estufa plástica é heterogênea, favorecendo uma grande variabilidade na fitomassa dos frutos de pimentão. Na figura 1 C e D, observam-se as relações, provenientes dos resultados obtidos pelo método de Hatheway.

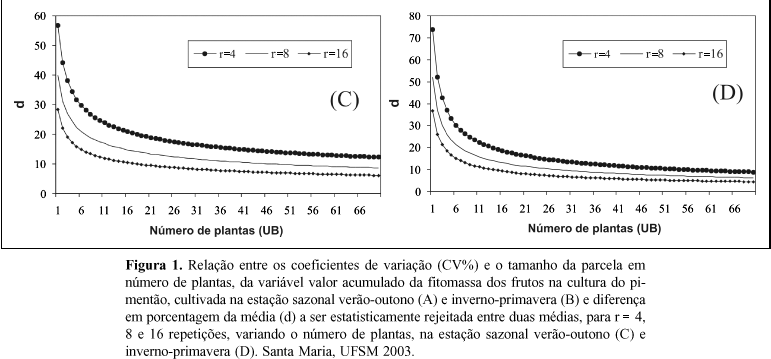
Para valores de "A" e d fixos, o tamanho de parcela decresce com o aumento do número de repetições e do índice de heterogeneidade do solo (b); enquanto que, para "A" e r fixos, o tamanho de parcela decresce com o aumento da diferença porcentual entre dois tratamentos a serem comprovados estatisticamente (d) e do índice b, e, para d e r fixos, ele cresce com o aumento do coeficiente de variação e do índice b. Portanto, parcelas menores, com maior número de repetições, permitem detectar menos diferenças percentuais entre tratamentos do que parcelas maiores, com um menor número de repetições.

A partir destes resultados, o pesquisador pode estabelecer o tamanho da parcela, conforme a diferença mínima entre tratamentos que deseja detectar. Em relação aos dois experimentos realizados com o pimentão, a seguir é demonstrado um exemplo baseado nas figuras 1 C e D: se a diferença mínima em porcentagem da média entre tratamentos desejada for de vinte por cento (20%), no experimento da estação sazonal verão-outono (Figura 1 C), pode ser detectada com quatro repetições de parcelas de dezenove plantas; ou com oito repetições de parcelas de nove plantas; ou ainda, com dezesseis repetições de parcelas de quatro plantas. Já no experimento da estação sazonal inverno-primavera (Figura 1 D), uma diferença mínima em porcentagem da média entre tratamentos de vinte por cento (20%) pode ser obtida com quatro repetições de parcelas de quinze plantas; ou com oito repetições de parcelas de oito plantas; ou ainda, com dezesseis repetições de parcelas de quatro plantas.

Os métodos da máxima curvatura e o de Hatheway apresentaram valores diferentes dos obtidos pelo método da comparação das variâncias, independentemente da estação sazonal de cultivo com pimentão sob estufa plástica.

Os valores estimados dos índices de heterogeneidade do solo "b" foram próximos a um, o que indica uma grande variabilidade na fitomassa dos frutos de pimentão cultivados nesta estufa plástica, independente da estação de cultivo.

O tamanho e a forma ótimos de parcela, obtidos pelo método da máxima curvatura, foram de dez plantas, sendo duas no comprimento e cinco na largura, para o experimento da estação sazonal verão-outono. Foram encontrados nove plantas como resultado pelo método de Hatheway ao se levar em consideração uma diferença mínima em porcentagem da média entre tratamentos (d) de 20% e um número de repetições (r) igual a oito.

Para o experimento da estação sazonal inverno-primavera, o tamanho e a forma ótimos de parcela, obtidos pelo método da máxima curvatura, também foram de dez plantas, sendo duas no comprimento e cinco na largura. Pelo método de Hatheway, com utilização de uma diferença mínima em porcentagem da média entre tratamentos (d) de 20% e de um número de repetições (r) igual a oito, o tamanho e a forma ótimos de parcela foram de oito plantas.

À Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul pelo auxílio financeiro para a realização do trabalho.

COCHRAN, W.G.; COX, G.M. Experimental designs. 6ed. New York: Wiley & Sons, 1968. 616 p.

HATHEWAY, W.H. Convenient plot size. Agronomy Journal, Madison, v.53, p.279-280, 1961.

LESSMAN, K.J.; ATKINS R.E. Optimum plot size and relative efficiency of lattice designs for grain sorghum yield tests. Crop science, Madison, v.3, p.477-481, 1963.

LOPES, S.J.; STORCK, L.; HELDWEIN, A.B.; FEIJÓ, S.; DA ROS, C.A. Técnicas experimentais para tomateiro tipo salada sob estufas plásticas. Ciência Rural, Santa Maria, v.28, n.2, p.193-197, 1998.

OLIVEIRA, P.H.; ESTEFANEL, V. Tamanho e forma da parcela para avaliação do rendimento em experimentos com batata. Ciência Rural, Santa Maria, v.25, p.20-220, 1995.

ORTIZ, R. Plot techniques for assessment of bunch weight in banana trials under two systems of crop management. Agronomy Journal, v.87, p.63-69, 1995.

RESENDE, M.D.V.; SOUZA JÚNIOR, C.L. Número de repetições e tamanho da parcela para seleção de progênies de milho em solos sob cerrado e fértil. Pesquisa Agropecuária Brasileira, Brasília, v.32, n.8, p.1457-1461 ,1997.

STEEL, R.G.D.; TORRIE, J.H.; DICKEY, D.A. Principles and procedures of statistics: a biometrical approach. 3ed. New York: McGraw-Hill, 1997. 666 p.

STORCK, L. Estimativa para tamanho e forma de parcela e número de repetições para experimentos com milho (Zea mays L.).Porto Alegre: UFRG, 1979. 98 p. (Tese mestrado) UFRGS, 1979.

STORCK, L.; SACCOL, A.V.; SCHNEIDER, F.M. Comparação de métodos de estimativa do índice de heterogeneidade do solo e do tamanho ótimo de parcela em experimento com soja. Ciência Rural, Santa Maria, v.12, n.2-3, p.189-202, 1982.

STORCK, L.; UITDEWILLIGEN, W.P.M. Estimativa para tamanho e forma de parcela e número de repetições para experimentos com milho (Zea mays L.). Agronomia Sulriograndense, Porto Alegre, v.16, n.2, p.269-282, 1980.

STORCK, L.; GARCIA, D.C.; LOPES, S.J.; ESTEFANEL, V. Experimentação vegetal. Santa Maria: Ed. UFSM, 2000. 198 p.

TAKAZAKI, P.E. Produção de sementes adaptadas ao ambiente protegido. In: SIMPÓSIO NACIONAL SOBRE PLASTICULTURA, 1, 1989, Jaboticabal. Anais... 2° ed. Jaboticabal: FUNEP, 1991, p.63-70.

VALLEJO, R.L.; MENDOZA, H.A. Plot technique studies on sweet potato yield trials. Journal of the American Society for Horticultural Science, v.117, n.3, p.508-511, 1992.

ZANON, M.L.B.; STORCK, L. Tamanho ótimo de parcelas experimentais para Eucalyptus saligna Smith em dois estádios de desenvolvimento. Cerne, Lavras, v.6, n.2, p.104-111, 2000.