 Página anterior Página anterior |   Voltar ao início do trabalho Voltar ao início do trabalho | Página seguinte  |
3. INDICE DE SATISFAÇÃO DAS NECESSIDADES DE ÁGUA
Entre os parâmetros obtidos a partir da simulação do balanço hídrico, destaca-se o índice dado pela relação entre a evapotranspiração real e a evapotranspiração máxima (ETR/ETM), ou seja, a quantidade de água que a planta consumiu e a que seria desejável para garantir plenamente a sua máxima produtividade conhecido como Índice de Satisfação das Necessidades de Água (ISNA) ou índice de penalização (Assad et al., 1988).
Para a simulação do balanço hídrico são computados: a precipitação pluviométrica diária, com um mínimo de 15 anos de dados; capacidade de armazenamento de água do solo; coeficiente de cultura (Kc), evapotranspiração potencial, duração do ciclo e duração das fases fenológicas da cultura.
O ciclo da planta, é dividido em quatro fases fenológicas: germinação-emergência, vegetativa; floração-enchimento de grãos e maturação .
O período de enchimento de grãos, é considerado o período crítico para as culturas, em termos de dependência de água. São então calculados os ISNAS médios dessa fase, para cada ano da série histórica e, em seguida, é realizada uma análise freqüêncial para 20, 50 e 80% de ocorrência. Somente a frequência de20% é espacializada pois sendo a mais conservadora, indica se o índice é maior ou igual a um certo valor para oito em cada 10 anos, isto é, em 80% dos anos (Assad et al., 1988).
4.1. MÉDIA MÓVEL PONDERADA
O interpolardor média ponderada calcula o valor de cota (z), de cada ponto da grade, a partir da média ponderada das cotas dos 8 vizinhos mais próximos, porém atribui pesos variados para cada ponto amostrado através de uma função w(x,y) que considera a distância do ponto cotado ao ponto da grade.
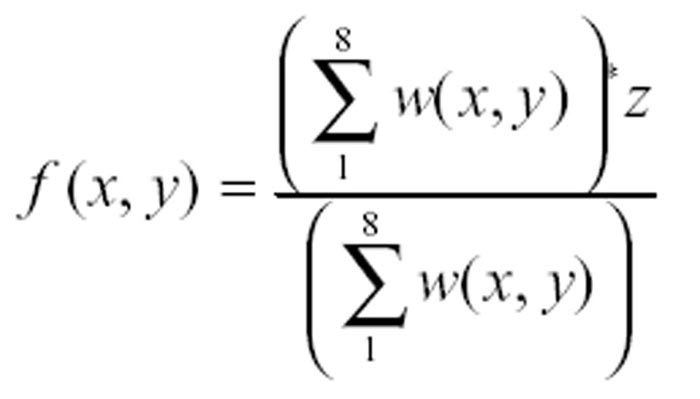 (1)
(1)
Um estimador determinístico por média móvel pode considerar a anisotropia do atributo a partir da definição do raio de busca dos vizinhos, que variam com a distância e com a direção. Entretanto na determinação dos pesos das amostras vizinhas por krigeagem, há um formalismo mais rigoroso tendo em vista que tem sua base no modelo de correlação espacial denominado variografia (Felgueiras, 2000).
4.2. KRIGEAGEM ORDINÁRIA
A krigeagem é um procedimento de inferência espacial estocástico que apresenta uma etapa de análise variográfica anterior aos procedimentos inferenciais onde a estrutura de covariância espacial é modelada (Fuks, 1998).
De acordo com Felgueiras (2000), um estimador de krigeagem ordinária, utiliza médias locais ou tendências locais estimadas a partir das amostras vizinhas, ao invés de uma única média estacionária, como o faz um algoritmo de krigeagem simples. Os valores (z) são estimados em localizações espaciais não observadas (u), sem a necessidade de se conhecer a média estacionária m, segundo uma combinação linear dos valores de um subconjunto amostral local. A condição para isso é a somatória dos ponderadores da krigeagem ordinária l0a (u) seja igual a 1.
O estimador de krigeagem ordinária é dado por:
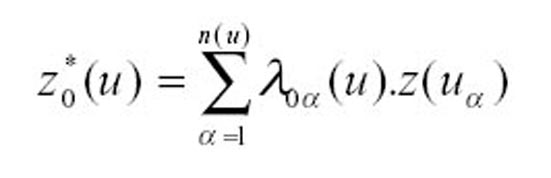 (2)
(2)
A variância do erro de estimação, conhecida como variância de krigeagem também pode ser traçada para informar sobre a confiança dos valores interpolados sobre a área de interesse (Burrough, 1998). Entretanto baseia-se apenas na localização geométrica do atributo não considerando a variabilidade do atributo. Isso implica em que o resultado fornecido é apenas uma comparação entre diferentes configurações geométricas, conforme já observado por Deutsch e Journel (1998), citados por Felgueiras (2000).
4.3. KRIGEAGEM POR INDICAÇÃO
Krigeagem por indicação pode ser definida como uma técnica de inferência estatística, que permite a estimativa dos valores e das incertezas associadas ao atributo durante o processo de espacialização de uma propriedade amostrada. A propriedade em estudo é considerada uma variável aleatória em cada posição u não amostrada, e as inferências dos valores z(u) e das incertezas são obtidos a partir da construção da função de distribuição acumulada, (F*(u;zk|(n)) condicionada aos n dados amostrados, de cada variável aleatória (Felgueiras et al., 1999).
Trata-se de uma técnica de inferência estatística não linear, pois é aplicada sobre os valores do atributo transformados por um mapeamento não linear, a codificação por indicação. São então definidos valores de corte, zk, k=1,2...,K, em função do número de amostras.
O estimador de krigeagem de indicação é dado pela expressão abaixo, considerando-se a somatória dos pesos de ponderação l0a(u;zk) igual a 1,
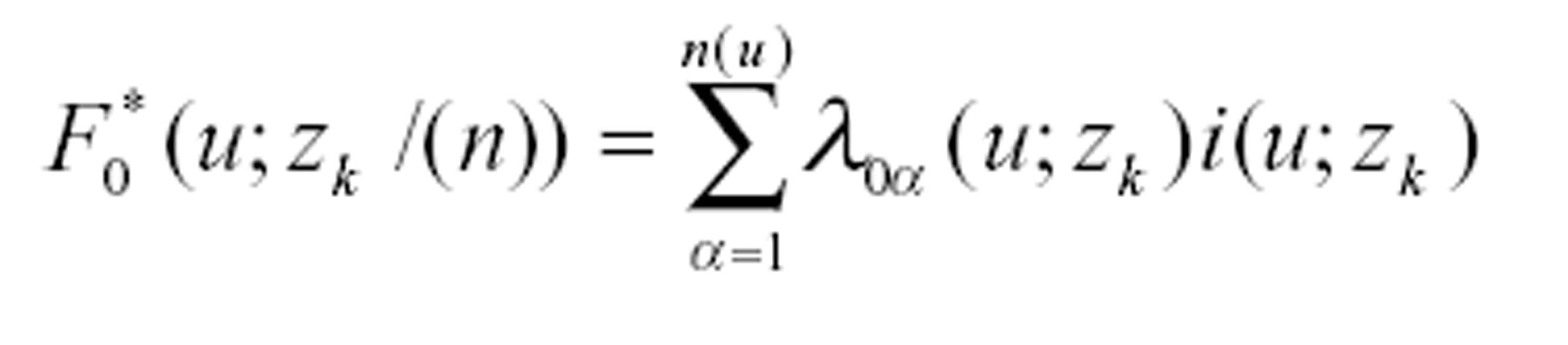 (3)
(3)
De acordo com Felgueiras (2000), a krigeagem por indicação é tida como não-paramétrica, por não considerar nenhum tipo de distribuição de probabilidade a priori para a variável aleatória. Ao invés disso, ela possibilita a construção de uma aproximação discretizada da função de distribuição acumulada da variável aleatória. Os valores de probabilidade discretizados podem ser usados diretamente para se estimar valores estatísticos característicos da distribuição, tais como: média, variância, mediana, quantis, etc.
Os dados utilizados, de domínio público, referem-se ao ISNA da terceira fase fenológica (período de enchimento de grãos) da cultura do milho ciclo médio, obtido por meio do balanço hídrico, para o dia 25 de novembro. Esses dados georreferenciados correspondem, geograficamente, à localização das 252 estações pluviométricas do Estado do Rio Grande do Sul.
Foram consideradas 3 classes de ISNAS para a cultura do milho ciclo médio:
· ISNA maior ou igual a 0,55 ® o plantio é favorável naquela data;
· ISNA maior que 0,45 e menor que 0,55 ® risco médio para o plantio naquela data;
· ISNA menor que 0,45 ® alto risco de perdas agrícolas para aquela data, sendo portanto considerada desfavorável.
Para realização dos procedimentos de interpolação a que os dados foram submetidos, utilizou-se o Sistema de Processamento de Informações Georreferenciadas Spring. INPE.
5.1 MÉDIA PONDERADA
Os dados foram primeiramente submetidos ao procedimento de interpolação pela média ponderada, o que é realizado de forma direta e automática nos diversos SIGs, bastando selecionar o interpolador desejado entre os disponíveis.
5.2. KRIGEAGEM ORDINÁRIA
A partir de uma análise exploratória dos dados, etapa importante dentro de qualquer estudo geoestatístico, realizada com base na observação do histograma e gráfico abaixo ( figura 5.1 a e b), foi suposta a hipótese de normalidade dos dados:
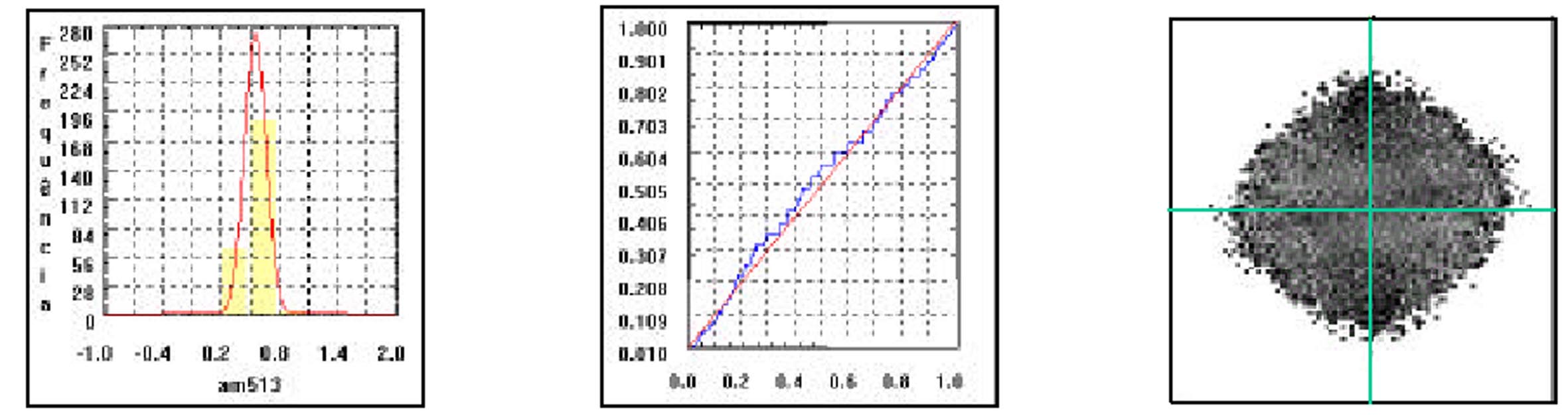
a) Histograma b) Gráfico da probabilidade Normal c) Superfície do variograma
Figura 5.1. Elementos gráficos para Análise Exploratória e de Superfície.
A análise de superfície (figura 5.1 c), necessária para verificação da continuidade espacial do atributo, mostrou que os dados em questão possuem distribuição espacial isotrópica, desta maneira um único modelo foi suficiente para descrever a sua variabilidade espacial.
A modelagem do semivariograma, a etapa na qual foi modelada a interpretação da estrutura de correlação espacial utilizada nos procedimentos inferenciais da krigeagem, envolveu o levantamento do semivariograma experimental; ajuste a uma família de modelos de semivariogramas; e a validação do modelo a ser utilizado nos procedimentos da krigeagem.
O ajuste de um semivariograma é um processo interativo no qual buscou-se adequar o variograma experimetal a um modelo teórico. Foram introduzidos valores para os parâmetros: incremento (distância máxima entre duas amostras em que ainda haja correlação entre elas), lag, (distância pré-definida utilizada no cálculo do semivariograma), e tolerância (deve corresponder aproximadamente à metade do valor do incremento para que não haja sobreposição considerável da área de influência).
Deste modo foi obtido o variograma experimental, o qual é formado por uma série de valores sobre os quais deseja-se ajustar uma função.
Uma vez obtido o semivariograma experimental, procurou-se realizar o seu ajuste aos modelos teóricos. O passo seguinte, validação do variograma, consistiu na re-estimação dos valores conhecidos de cada ponto amostrado da área. Este procedimento permite identificar possíveis erros de estimativa.
O bom ajuste pode ser verificado pelo diagrama onde encontram-se plotados os valores observados e inferidos, pelo histograma do erro, e diagrama espacial do erro (figuras 5.2 a, b e c.).
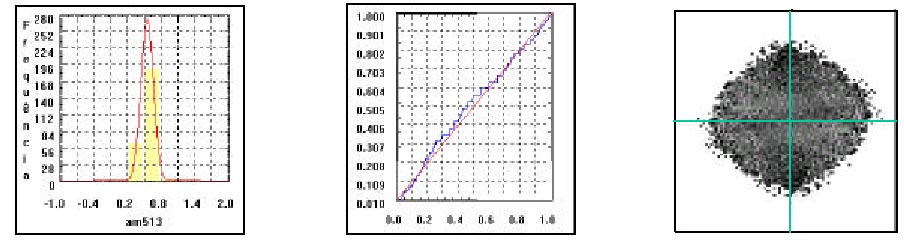
a) Observados X estimados b) Histograma c) Diagrama espacial do erro
Figura 5.2. Resultado da re-estimação dos pontos amostrais para a krigeagem ordinária.
Em seguida foi realizado o procedimento de krigeagem para espacialização do ISNA, a partir dos parâmetros obtidos nas etapas acima descritas.
5.3. KRIGEAGEM POR INDICAÇÃO
Para execução da krigeagem por indicação, os valores do atributo foram organizados em ordem crescente e em seguida divididos em decis, definindo-se 9 valores de corte abaixo dos quais os valores das amostras são transformados em 1 e acima destes em 0, gerando assim um conjunto amostral por indicação.
Para os dados analisados, cujo valores variam entre 0.18 a 0.83, foram definidos os seguintes valores de corte: 0.395, 0.465, 0.505, 0.535, 0.565, 0.585, 0.605, 0.645, 0.685. Para cada valor de corte, foi gerado um semivariograma, os quais foram ajustados aos modelos teóricos conforme realizado para a krigeagem ordinária.
Os valores dos atributos, foram estimados pelo valor médio e os valores de incerteza local são correspondem a dois desvios padrão, sendo definidos o mínimo de um e máximo de oito pontos na área de busca.
A figura 6.1 a, b e c mostra as imagem em níveis de cinza obtidas pelo interpolador média ponderada, krigeagem ordinária e krigeagem por indicação respectivamente.
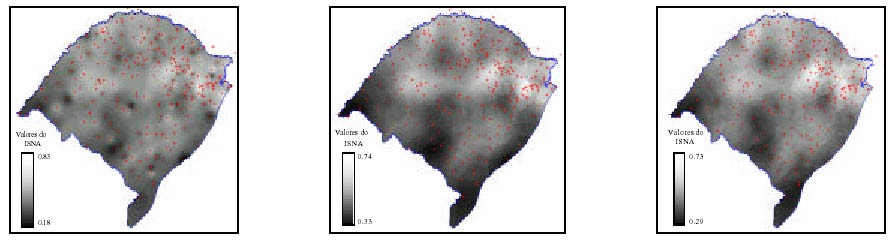
a) Média ponderada b) Krigeagem ordinária c) krigeagem por indicação
Figura 6.1. Superfícies geradas pelos métodos de interpolação.
À primeira vista os resultados são semelhantes para os três métodos, entretanto pode ser notado que a superfície gerada pelos métodos geoestatísticos, sobretudo a krigeagem por indicação é mais suave. Conforme já observado por Camargo (2000), o ponto crítico ocorre justamente onde há subestimação e superestimação do valor do atributo, que no resultado gerado pela krigeagem por indicação ocorre de maneira gradual, mais coerente, portanto, com o que ocorre na natureza.

a) Variância de krigeagem b) Incertezas locais
Figura 6.2. Variância de krigeagem e das incertezas locais associadas às inferências.
A variância do erro de estimação (figura 6.2 a) fornece informações a respeito da confiabilidade dos valores interpolados, o que representa uma importante vantagem sobre o método da média ponderada, onde os valores inferidos são tratados como dados sem erro.
Entretanto a variância de krigeagem é obtida em função do estimador e da distribuição espacial das amostras, não considerando o valor do atributo. Pode-se observar que onde os valores interpolados coincidem com os pontos amostrais a variância é zero, e aumenta com a distância dos mesmos.
Diferentemente da observação anterior, o mapa de incertezas locais (figura 6.2 b), fornecido pela krigeagem por indicação, utiliza a função de distribuição acumulada condicionada da variável aleatória que representa o atributo, independentemente do estimador. Assim, maiores incertezas são encontradas onde o valor do atributo tem maior variação enquanto a ocorrência de valores com menor variação geram superfícies mais suaves caracterizando menor incerteza.
Os cartogramas abaixo são resultado do fatiamento das grades geradas pela média ponderada, krigeagem ordinária e krigeagem por indicação. Algumas diferenças podem ser observadas no resultado obtido pelos diferentes métodos. Tendo em vista que a condição para obtenção do seguro agrícola seja a inserção do município na área definida como favorável, algumas diferenças, embora sutis, podem ser observadas na configuração das classes, o que afeta principalmente aos municípios de menor área.
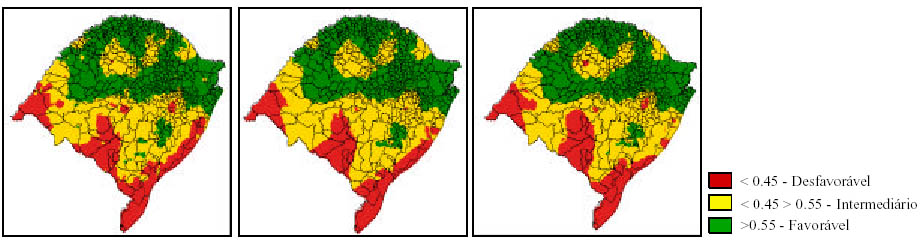
a) Média ponderada b) Krigeagem ordinária c) Krigeagem por indicação
Figura 6.3. Fatiamento das grades geradas pelos diferentes interpoladores.
O trabalho mostrou o potencial e a viabilidade da utilização de métodos geoestatísticos como alternativa aos modelos inferenciais determinísticos, na espacialização do Índice de Satisfação das Necessidades de Água, o ISNA.
Além de possibilitar a definição da forma e orientação do domínio a ser considerado na interpolação, e de atribuir pesos às amostras levando em conta a variabilidade do atributo na área, os interpoladores geoestatísticos permitem ainda modelar as incertezas associadas às inferências.
Foi possível observar ainda que, embora a krigeagem ordinária tenha se apresentado como um interpolador robusto, em relação à média ponderada, apresentou algumas desvantagens em relação a krigeagem por indicação. Com relação a informações relacionadas à confiabilidade dos dados interpolados. Enquanto a krigeagem ordinária considera apenas a distribuição espacial dos pontos amostrais, a krigeagem por indicação leva em conta a variabilidade do atributo, permitindo uma análise da incerteza dos valores nos locais não amostrados.
Além disso a krigeagem por indicação destacou-se entre os métodos utilizados por ter aplicação mais ampla, pois seria possível utilizá-la ainda que a distribuição do dado aqui analisado não fosse normal, e que possuísse valores fora da tendência, o que poderia ocorrer uma vez que, neste trabalho, foi espacializado apenas o ISNA para uma data específica entre as dezessete disponíveis para a cultura do milho (Zea mays) ciclo médio.
Uma consideração prática diz respeito justamente a quantidade de dados e à urgência em disponibilizá-los. Tanto a krigeagem ordinária, e mais ainda, a krigeagem por indicação, são processos interativos, onde o analista busca adequar o variograma experimental a um modelo teórico, o que pode não ser um processo rápido, ainda mais se, no caso da krigeagem por indicação, forem definidos vários valores de corte.
O ISNA define a data de plantio onde o risco de perdas na agricultura seja menor. Diante da importância desse dado e das conseqüências práticas da sua espacialização, identificou-se a krigeagem por indicação como o método mais adequado, entre os aqui analisados, a esse atributo, por permitir, inclusive, uma análise mais confiável da qualidade da informação gerada.
REFERÊNCIAS BIBLIOGRÁFICAS
Mariza Alves De Macedo1; Julio Cesar De Oliveira2; Alda Monteiro Barbosa3; Gilberto Câmara4; Eduardo Delgado Assad5
gilberto[arroba]dpi.inpe.br
INPE – Instituto Nacional de Pesquisas Espaciais
Pós-Graduação em Sensoriamento Remoto
Caixa Postal 515. CEP 12201-097. São José dos Campos. SP, Brasil.
1. mariza[arroba]ltid.inpe.br ; 2 oliveira[arroba]ltid.inpe.br ; 3 alda[arroba]ltid.inpe.br ;
4. Divisão de Processamento de Imagens gilberto[arroba]dpi.inpe.br
5. EMBRAPA. Cerrados Br 020. Km 18. CEP. 7330-970. Planaltina. DF, Brasil. assad[arroba]cpac.embrapa.br
![]()
Estas obras estão licenciadas sob uma Licença Creative Commons
 Página anterior Página anterior |   Voltar ao início do trabalho Voltar ao início do trabalho | Página seguinte  |
|
|
|