Regresión lineal múltiple (página 2)

Partes: 1, 2

Forma matricial del modelo
Habitualmente escribimos el modelo como
Y = Xb + U
con:

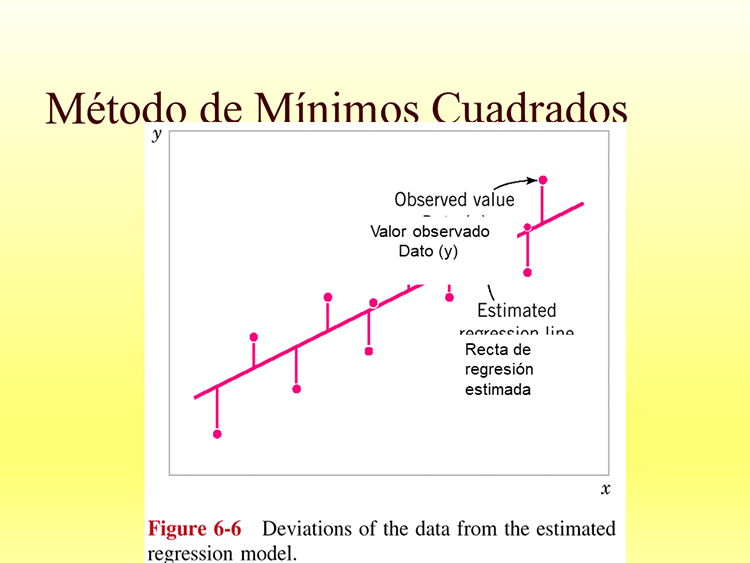
Método de Mínimos Cuadrados
Valor observado
Dato (y)

Recta de regresión
estimada

Valor observado
Dato (y)

Recta de regresión
estimada

Mínimos Cuadrados
Objetivo: Buscar los valores de b0,b1,…,bk que mejor ajustan nuestros datos.
Ecuación:

Residuo:

Minimizar:

Mínimos Cuadrados
Resultado en forma matricial:

Interpretación geométrica
Hemos calculado:

Tenemos:

Definimos la matriz:

H es idempotente, simétrica y del mismo rango
que X, (k+1). Es una matriz de proyección.

Interpretación geométrica
H simétrica (obvio)
H idempotente

Residuos ortogonales a valores ajustados

Residuos ortogonales a matriz de diseño X

Interpretación geométrica
Subespacio vectorial generado por las columnas de X

Varianza
Para estimar s2 utilizamos la varianza residual

Es insesgado como estimador de s2 y además

Propiedades de los estimadores
Normalidad. Sabemos Y=Xb +U, de donde Y~N(Xb,s2I).
Como también es normal.
Esperanza.

Varianza.

Propiedades de los estimadores
Tenemos

La varianza s2 suele ser desconocida y utilizamos
el error estándar estimado

Inferencia. Contrastes para b
Para averiguar si la variable xi afecta a la
respuesta, debemos plantear el contraste

Rechazamos la hipótesis nula si:

Inferencia. Int. de confianza para b
Podemos construir un intervalo de confianza
para bi con nivel de confianza 1-a como

Si n > 30 y a = 0.05, sabemos que tn-k-1,a/2 @ 2.

Descomposición de la variabilidad
Igual que en la regresión simple VT=VE+VNE

Coeficiente de determinación
El coeficiente de determinación se define:

El coeficiente de determinación ajustado es más interesante ya que sólo aumenta si disminuye la varianza residual

Contraste de regresión (fuera programa)

Para averiguar si existe relación lineal entre la
variable respuesta y las explicativas, realizamos

Rechazamos la hipótesis nula si:

Predicción para la media
Buscamos estimador puntual e I.C. para el valor medio de la respuesta cuando x=x0

Predicción para la media
El intervalo de confianza para la media que obtenemos es:

Ejemplo: semiconductores
¿Cuál sería el I.C. para para la respuesta media si la longitud del cable es 8 y la altura de la estructura es 275?

Ejemplo: semiconductores

Predicción para una nueva observación
Intervalo de predicción

Ejemplo: semiconductores (long. 8, altura 275)

Multicolinealidad
Problema frecuente que se presenta cuando las variables explicativas son muy dependientes entre sí.
No es un problema del modelo, sino de los datos, surge cuando det(XtX) próximo a cero.
Las variables explicativas son significativas en el modelo simple, pero dejan de serlo en el múltiple.

Índice de condicionamiento
Los autovalores de XtX son mayores o iguales que cero, para que haya multicolinealidad, alguno tiene que ser aproximadamente cero.

Si 10 £ Ind.Cond. £ 30, multiolinealidad moderada
Si Ind.Cond. > 30, multicolinealidad alta

Ejemplo: Sabor del queso

Ejemplo: sabor del queso
Multicolinealidad moderada

Ejemplo: sabor del queso

Ejemplo: sabor del quesoRegresión simple Láctico
Antes 30.73

Ejemplo: sabor del quesoRegresión simple Acético
Antes 3.9